基于马氏距离和稀疏矩阵技术的激光诱导击穿光谱(LIBS)煤质灰分分析
2022-09-22李盛冬倪明辉
李盛冬 倪明辉 许 斐 韦 祎 李 燕*
(1.国能南京煤炭质量监督检验有限公司,南京 210031;2.南京理工大学 化学与化工学院,南京 210094)
煤炭在未来相当长一段时间内仍将是我国使用量最大的燃料能源,煤炭的清洁高效利用是中国低碳经济的关键,快速煤质分析技术则是保障煤炭资源有效利用的必要前提。传统的煤质分析主要靠离线实验室化验分析,过程耗时较长,滞后性严重,不利于对锅炉燃烧提供实时指导。而已有的快速检测技术存在种种问题而不实用,如:X射线荧光光谱法不能检测原子序数小于11的轻元素,γ射线中子活化法存在中子辐射危害,严重影响操作人员的健康,且维护成本高等问题。激光诱导击穿光谱(Laser-Induced Breakdown Spectroscopy,LIBS)技术具有无需制样、对样品损伤小、多元素同时分析、检测速度快等优点[1-2],在煤中元素含量和工业指标分析中受到了广泛关注[3]。
偏最小二乘回归(Partial Least Square Regression,PLSR)是LIBS定量分析中应用较为广泛的一种建模方法,在LIBS光谱煤元素含量分析和工业指标分析中得到了广泛重视[4-5]。该算法相比于其他多元线性回归方法,很好地解决了由于样本点数过少导致的回归难题或变量之间存在多重相关性的问题。因此,本文选择PLSR用于煤的LIBS光谱定量分析,综合考虑了以下两点因素:1)基体效应、随机噪声、光谱干扰和自吸收的影响,可以在光谱矩阵分解提取中得到消除;2)PLSR适合于样本数量较少的情况[6]。
由于受到实验仪器性能波动和环境因素的影响,实际测得的光谱数据通常会有较大的波动,甚至出现一些异常值,影响光谱数据的稳定性。此外,LIBS系统实验参数的不稳定性,样品表面形态的不规则,采样时间延迟等因素的存在,不可避免地导致LIBS光谱中产生连续背景噪声,从而引起基线漂移,严重影响光谱定量分析的精度。因此,本文研究了基于马氏距离(Mahalanobis Distance,MD)的异常值剔除算法和基于稀疏矩阵技术的基线估计与降噪算法(Baseline Estimation And Denoising using Sparsity,BEADS)在改善光谱信号质量中的作用,该方法在一定程度上提高了PLSR模型的预测性能。
1 实验过程
1.1 实验装置
激光诱导击穿光谱的工作原理是使用高能量的激光光源聚焦后打在煤饼表面,形成高温、高密度的等离子体,等离子体以光的形式向外辐射能量,通过光谱仪即可采集到包含多种元素特征谱线的光谱信号。理论上来说,元素的特征谱线强度与其含量成正比,而煤的热值、灰分、挥发分等工业指标与特定元素的含量也具有相关性,因此利用数学分析模型进行光谱数据的分析处理,即可实现煤质工业指标的快速检测。
图1所示为LIBS测量装置示意图,该系统主要由高能脉冲激光器、多通道光纤光谱仪、光学组件、样品承载平台和计算机等组成。其中,激光器的脉宽6 ns,工作波长为1 064 nm,激光能量0~100 mJ可调,激光工作频率为1~10 Hz,激光聚焦斑点直径为50~800 μm;多通道光纤光谱仪的最小积分时间为1.05 ms,延迟时间可调。样品置于自动控制的样品步进位移平台上,通过计算机设置好运动轨迹,可使激光每次打在样品表面的不同位置处,一定程度上消除背景噪声的影响。等离子体光信号通过侧向45 °布置的光纤探头收光,再传输到多通道光谱仪,光谱数据通过USB传输至计算机。
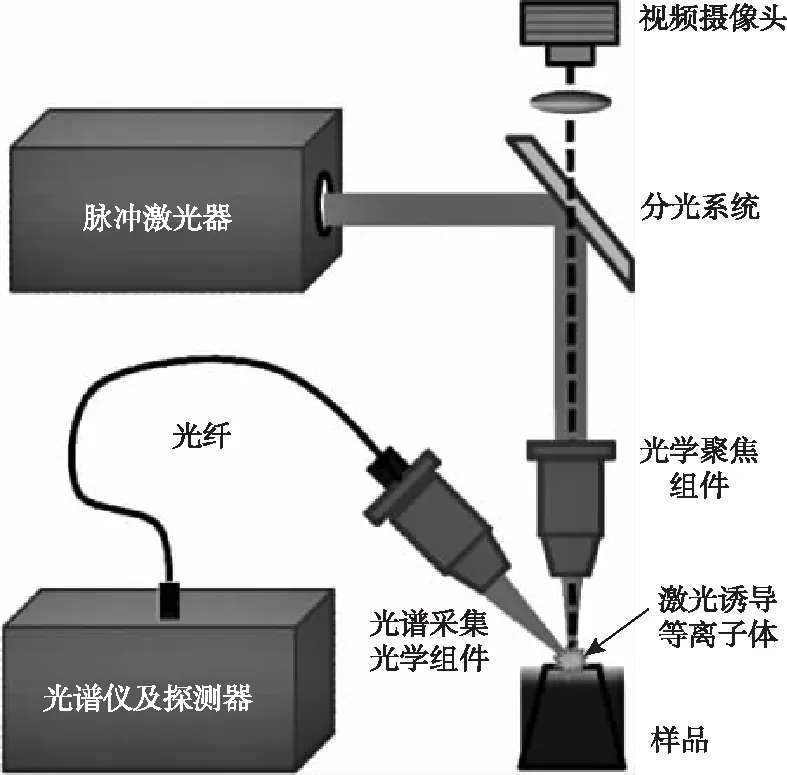
图1 LIBS煤质分析测量装置示意图Figure 1 Schematic diagram of the LIBS coal analysis instrument.
综合考虑信噪比、光谱强度等对实验参数进行了优化,优化的实验参数为:激光能量100 mJ,延迟时间1 μs,激光工作频率3.3 Hz,聚焦斑点直径500 μm。对于每个样品,共采集324个点的光谱数据,并将其平均后光谱作为该样品的原始光谱数据。
1.2 实验煤样
共测试20个煤样,分别将煤样研磨为200 μm粒径的煤粉,将约3 g粒径为200 μm的煤粉放入直径为30 mm的模具中,利用电动液压压片机在277 MPa下压制成煤饼,使样品表面平整。所用煤样的灰分含量如表1所示。将20个煤样分为训练集和测试集两组,选取#15、#16、#17、#18、#19、#20这六个样品作为测试集,其余14个样品为训练集。
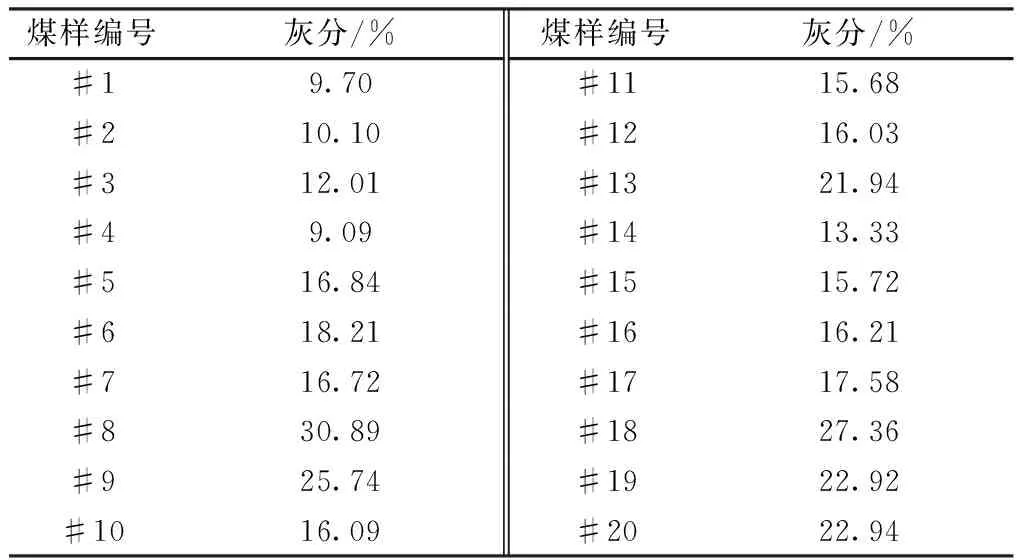
表1 20种煤样品的灰分含量Table 1 Ash content of 20 coal samples
1.3 模型评价指标
采用以下指标评估PLSR模型性能:1)拟合度(R2);2)均方根误差(RMSE);3)预测均方根误差(RMSEP),这是从整理上评价模型的性能;4)平均绝对误差(MAE);5)平均相对误差(MRE),这是从单次测量上评价模型预测的精度。计算公式见式(1)~(5):
(1)
(2)
(3)
(4)
(5)
2 数据处理
2.1 异常值剔除
在LIBS分析中,通过多次测量数据的平均处理时较为常用和简便的手段和方式,但均值处理只能削弱异常值的干扰,且次数过多会增加测量的成本和时间,通过异常值剔除可以有效提高数据的稳定性。马氏距离(MD)基于多元正态分布理论,考虑了多种因素的相互作用,不受量纲、单位的影响,是进行异常值剔除的一种有效方法[7-8]。
马氏距离计算公式如式(6)所示:
(6)
式中,d为各次激发光谱Y与样品平均光谱μ的马氏距离;Y为单次激发的光谱数据矩阵;μ为参考光谱平均值,本实验以自身多次激发的光谱为参考;Σ为参考光谱的协方差矩阵。
2.2 光谱基线校正
通常光谱去噪算法也可用于实现光谱的基线校正,如小波变换法、多项式拟合法、中值滤波法等,但这些基线校正算法原理都较为复杂,计算量大,且受到参数影响较大。本文采用NING等[9]提出的一种基于稀疏矩阵技术的基线估计与降噪算法(BEADS)进行基线校正处理。该算法计算效率高,适用于范围较广的光谱数据。
BEADS算法将信号Y同时分解为三种贡献[10]:
Y=[y1,y1,…,yn]=c+b+e
其中c、b、e参考了BEADS计算得到的稀疏光谱图、基线向量和噪声向量,它们依赖于一组工作参数p。工作参数是指截止频率(fc,由基线和其他贡献之间的边界构成)、不对称(r,惩罚负值)和正则化参数(λ0,λ1和λ2,控制向量c的稀疏性)。另一个参数是振幅(A),它乘以正则化参数;因此,正则化参数实际上是A×λi,这使得λi参数之间的比率与它们的大小无关。BEADS计算系统提供结果的质量在很大程度上取决于工作参数的正确选择,特别是截止频率,它对返回基线有重大影响。
2.3 特征谱线的筛选
煤的灰分是一项在煤质特性分析和研究中起到重要作用的指标,其含量越高,有效碳的含量就越低[11]。煤的灰分构成较为复杂,主要由矿物质构成,通常以氧化物的形式表示,如Al2O3、SiO2、Na2O、K2O、CaO、MgO、Fe2O3,因此在对灰分进行定量分析时选择与灰分相关的矿物元素的特征谱线作为灰分含量定标模型的输入变量。最终选定Si、Al、Fe、Na、Mg、K、Ca、Ti、Li这9种元素的谱线强度对煤中灰分进行回归分析。通过与美国国家标准与技术研究院(NIST)的原子光谱数据库(ASD)进行谱线波长的比对,对以上元素的特征谱线进行选择,如表2所示。

表2 煤中元素特征谱线Table 2 Characteristic spectral lines of coal elements
3 结果与讨论
首先使用马氏距离剔除异常数据。分别计算各样品的单次激发光谱与样品平均光谱之间的马氏距离,通过马氏距离的大小判断与总体情况差异较大的数据,同时考虑避免过度剔除造成信号失真,设置阈值将后100个数据予以剔除,保留70%的数据。分别计算特征谱线的绝对强度值在多次测量中的相对标准偏差(RSD)和平均绝对强度的变化情况。
图2所示为Fe(259.939 6 nm)谱线在异常值剔除前后的相对标准偏差RSD。可见,在利用马氏距离法进行异常值剔除后,谱线的RSD大大降低。
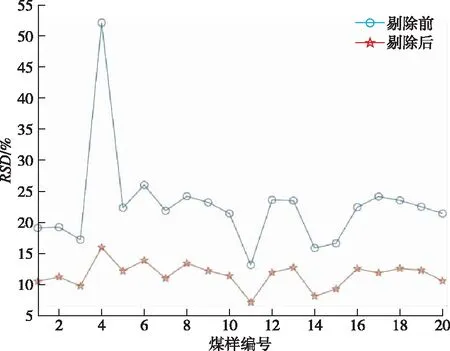
图2 异常数据剔除前后Fe(259.939 6 nm)谱线强度RSD比较Figure 2 RSD comparison of Fe(259.939 6 nm) spectral line intensity before and after removing abnormal data.
将马氏距离应用于其他谱线的异常数据剔除,结果如图3所示。
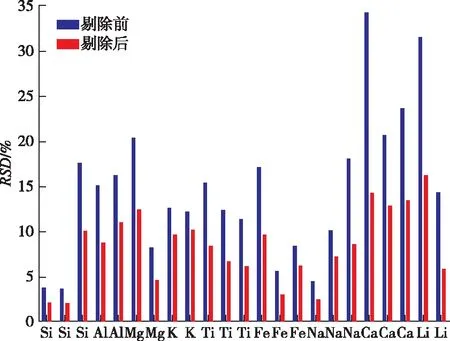
图3 #3煤样数据剔除前后各谱线强度RSD比较Figure 3 RSD comparison of spectral line intensity before and after data elimination of #3 coal sample.
从图2可以看出,Fe的特征谱线强度RSD的均值从22.63%降低至11.48%。图3也显示出,经过马氏距离剔除异常数据后,#3煤样的23条元素谱线强度RSD都大幅度下降,平均降低幅度为6.29%,这说明经过马氏距离剔除异常数据后,元素特征谱线强度的稳定性有了很大的提高。
之后使用BEADS算法对煤样光谱图进行基线修正和降噪处理,结果如图4所示。可见,经基线修正后,明显改善了多通道光谱仪中不同通道光谱信号的基线漂移情况。

图4 #1煤样光谱基线校正前后对比Figure 4 Comparison of #1 coal spectra before and after spectral baseline correction.
分别将20个煤样的光谱数据直接作均值处理和上述的预处理,之后选择上述的23条特征谱线的强度作为自变量矩阵,相应的灰分含量作为因变量矩阵。
主成分个数的选取对于偏最小二乘回归模型的效果有着关键影响,如果选择的主成分个数过少,就不能充分利用样品信息,导致拟合效果较差;若是选择的个数过多,则会将一些噪声信息加入到模型中,造成过拟合问题,使得模型的预测性能大大降低。本文采用留一交叉验证法(Leave One Out Cross Validation,LOO-CV)来检验模型内部稳健性和拟合效果,利用交叉验证均方根误差(Root Mean Square Error of Cross Validation,RMSECV)确立最优主成分个数,RMSECV越小,表明PLSR模型对训练集数据的拟合效果越好,计算公式见式(7):
图5为原始数据和预处理后数据得到的RMSECV结果,从图中可知最佳主成分个数分别为7和8。
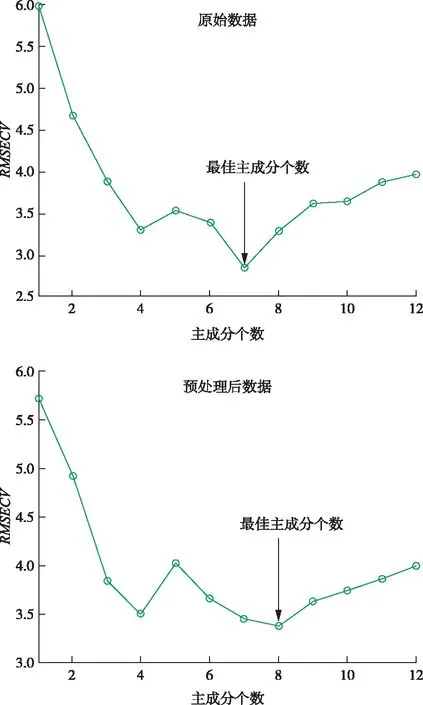
图5 交叉验证均方根误差与主成分个数关系Figure 5 Relationship between RMSECV and the number of principal components.
根据最佳主成分个数建立偏最小二乘模型。图6和图7分别是对原始数据和作预处理后数据的偏最小二乘回归预测结果,从中可以看出,通过马氏距离剔除和基线校正,训练集的拟合度(R2)从0.974 0提高到0.984 1,均方根误差(RMSE)从0.961 3降低到了0.752 7,这表明基于数据预处理可以一定程度地提高偏最小二乘拟合结果的准确性。分别用其模型预测测试集的煤样灰分值,预测均方根误差(RMSEP)从2.273 1降到2.001 7,模型的预测性能得到了一定的提升;同时平均绝对误差(MAE)和平均相对误差分别从1.974 7和0.109 4降低到1.557 2和0.075 7,表明单次测量精度也有所提高。
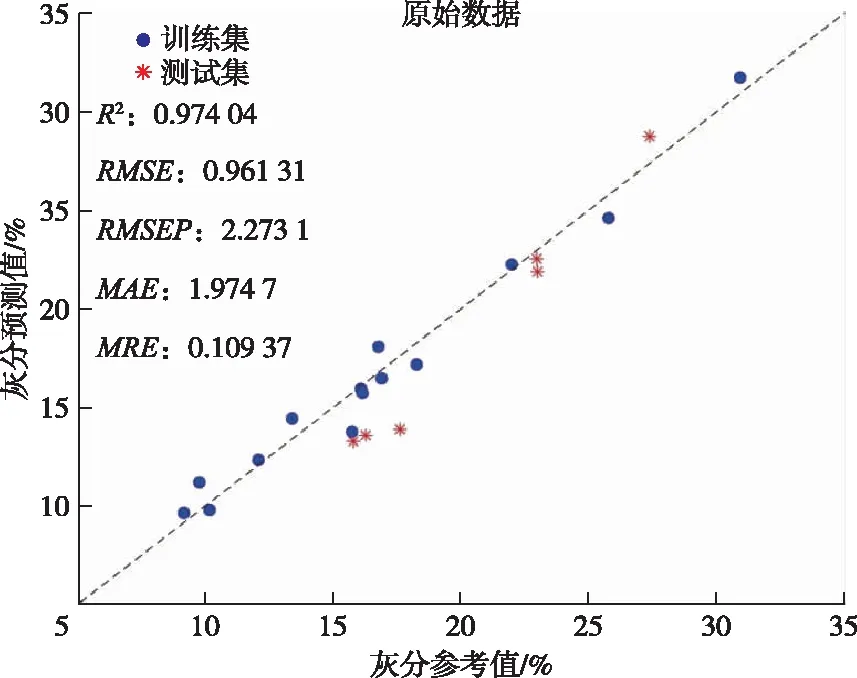
图6 基于原始数据的PLSR灰分预测模型Figure 6 Ash prediction results from PLSR based on raw data.

图7 基于预处理后数据的PLSR灰分预测模型Figure 7 Ash prediction results from PLSR based on pre-processed data.
4 结论
灰分含量是影响煤炭质量的关键工业指标,灰分的准确检测对煤炭的清洁高效利用具有重要意义。采用LIBS技术结合PLSR回归模型,应用于煤中灰分的快速准确检测是一种快速实时的检测手段。然而,对于多幅光谱数据,常用的均值处理方法不能完全降低谱线强度的波动性,本文通过使用马氏距离进行异常数据剔除后,再结合基于稀疏矩阵技术的基线估计与降噪算法进行谱图降噪处理,可以有效去除光谱中的噪声和异常值,提高谱线强度的稳定性。经过处理后,定标样品的拟合度(R2)从0.974 0提高到0.984 1,均方根误差(RMSE)从0.961 3降低到了0.752 7,预测均方根误差(RMSEP)从2.273 1降到2.001 7,模型的总体性能得到了一定的提升;同时平均绝对误差(MAE)和平均相对误差亦都降低,表明单次测量精度也有所提高。作为一种有效的数据预处理方法,此算法可用于复杂光谱数据的异常值剔除和光谱降噪,有利于提高定量分析模型的预测精度。
