基于状态空间模型的大型风力机运行模态及不确定性分析

张惊朝戴靠山，2，3施袁锋，2，*

（1.四川大学土木工程系，成都 610065；2.深地科学与工程教育部重点实验室，成都 610065；3.破坏力学与防灾减灾四川省重点实验室，成都 610065）

0 引言

风能作为一种遍布全球的可再生能源，备受全世界的重视，风电已逐步成为最具发展前景的清洁能源之一［1］。据全球风能理事会（Global Wind Energy Council，GWEC）统计，截至2019年底，全球累计风电装机容量约为650.6 GW，而2014年底约为369.8 GW，5年时间内将近增加了一倍［2］。为了更有效捕捉风能并提高风电经济效益，风力机组向着叶片更长和塔架更高的趋势发展。然而，大型风力机组长期在环境恶劣和荷载复杂条件下运行，各种风电场的运维问题也随之而来，尤其是风力机组因振动引起的损伤甚至倒塔带来的影响最为显著［3-6］。为延长风力机组的使用寿命以及减少运维成本，定期对风力机组进行结构健康监测是重要维护手段之一［7］，其中通过对风机结构进行模态分析获得其动力特性，是风机结构损伤识别和性能评估的主要手段之一［8］。

模态分析可分为试验模态分析（Experimental Modal Analysis，EMA）和 运 行 模 态 分 析（Operational Modal Analysis，OMA）［9］。EMA通常用激振器施加并测量人工激励以及获取相应的结构振动响应来开展模态分析。与传统的EMA相比，OMA无须对结构施加人工激励，仅需直接拾取结构在运行或环境激励下的振动响应来估计结构的模态参数，因此可避免人工激励对结构可能造成的损伤问题。Wang等［10］分别运用接触式和非接触式测量，对风力机展开OMA；孙溢膺等［11］采用随机子空间（SSI）法，应用于某风机模型实测中。尽管学者们在提出或者采用某种模态分析方法时，都进行了一些比较来说明识别结果的准确性，但大部分并没有真正考虑识别结果的不确定性问题。在模态分析中，由于数据有限、测量噪声、建模误差和激励未知等各种不确定因素的存在，一般不可能精确地识别出结构的模态参数［12］。实现模态参数不确定性量化，一方面，可以直接看出每个参数识别的精度，有利于对模态分析方法的评估；另一方面，有利于模型的修正，从而减少识别误差，得到更精准的识别结果［13］。Mares等［14］采用多元回归模型计算不确定参数的灵敏度矩阵，并利用梯度方法计算得到了模型参数的均值和协方差；姜东等［15］以三自由度体系和复合材料板为例，考虑识别结果的不确定性，提出了一种基于区间分析的不确定性结构动力模型修正方法。

目前，模态分析方法可以有效地识别风力机组停机工况下的模态参数［16-17］，但对于带有叶片旋转的风机运行状态下的识别结果往往存在不精准甚至失效的问题［18-19］。这主要是由于风机在运行状态下，叶片旋转会产生较大的气动阻尼、振动信号中带有明显的周期性成分以及识别算法中时不变系统和稳态随机激励的假设矛盾，影响了识别结果的准确性［16，20］。为此，董霄峰［21］利用一种考虑谐波修正的SSI方法，考虑了叶片转动对模态识别的影响；Dai等［22］提出了一种改进的SSI法，讨论了该方法在识别精度和稳定上的优越性以及对谐波频率、噪声程度与谐波幅度等干扰的鲁棒性，进而对某在役风机停机和运行工况下的模态参数进行识别并通过共振校核方法评估风机结构具有良好的运行安全性；孟欢等［23］利用快速傅里叶变换以及谱细化法，应用于两座5 MW海上风力机的现场实测数据中。

本文采用一种基于状态空间模型的运行模态及不确定性分析方法，以解决带有叶片旋转的风机结构的模态参数识别问题。最后，本文以实例分析一风机不同塔架方向的模态参数的差异性，以及不同工况下风机模态参数的变化情况，并结合识别结果的不确定性水平，证明该方法的实用性。

1 基于状态空间模型和极大似然估计的运行模态分析

1.1 随机状态空间模型

在环境激励下，长度为N的结构响应数据Y={y1，y2，…，yN}，可用离散时间随机状态空间模型进行模拟

式中：A∈Rn×n和C∈Rp×n分别为系统的状态矩阵和输出矩阵；xk∈Rn×1为系统在k时刻的n维状态向量，并假设系统初始状态向量x1服从正态分布x1～N(μ1，P1)；yk∈Rp×1为系统在k时刻的p维输出向量；wk、vk分别为系统的过程噪声和测量噪声，可模拟为均值为零的高斯白噪声，且两者的协方差表示为

式中：E(·)为数学期望因子；δpq为Kronecker delta函数。

式（2）考虑了系统过程噪声和测量噪声的相关性。这里，同时假设x1与(wk，vk)不相关。

随机状态空间模型式（1）的参数化形式具体可表示成

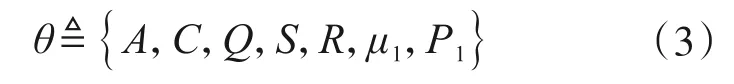
式中，θ为模型式（1）的参数变量，代表了系统所包含的所有自由变化参数组成的向量形式，系统的特性也完全由θ决定。

1.2 模型参数极大似然估计

系统参数θ可通过观测响应数据Y进行估计。由于极大似然估计方法具有渐近无偏估计、渐近一致性和渐近有效性等优异特性，本文采用极大似然法来实现随机状态空间模型参数θ的估计，进而获取结构的运行模态参数。

极大似然估计的关键在于似然函数的建立以及求解，但由于xk、wk以及vk未知，直接通过随机状态空间模型式（1）来构建似然函数难以实现，而结合卡尔曼滤波可以实现。式（1）的卡尔曼滤波可以表示［24］

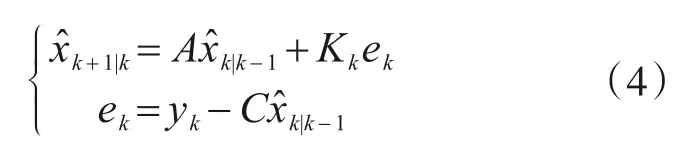
式中，

由于卡尔曼滤波式（4）得到的残差序列{ek(θ)}是不相关的高斯随机序列，由此可构造出数据Y的对数似然函数L(θ|Y)，去掉常数项后得

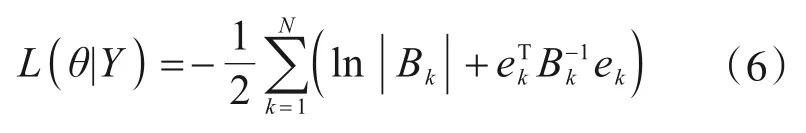
根据极大似然法的原理可知，系统参数θ的极大似然估计可表示为

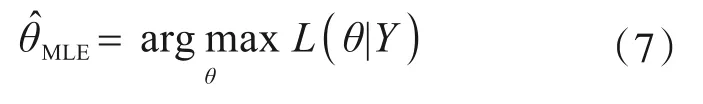
由于直接通过极大似然估计求解对数似然函数L(θ|Y)难以完成，本文应用EM迭代算法求解参数θ的极大似然估计值。

1.3 最大期望(EM)算法

EM算法是一种通过迭代进行极大似然估计的优化算法，主要用于包含隐含量的概率模型进行参数估计，即从观测数据Y中找到使对数似然函数L(θ|Y)最大化的估计参数θ［25］。假设系统的完整数据Z=(X，Y)由X，Y共同构成，其中，X为遗漏数据（未知），Y为观测数据。

由贝叶斯公式可知：

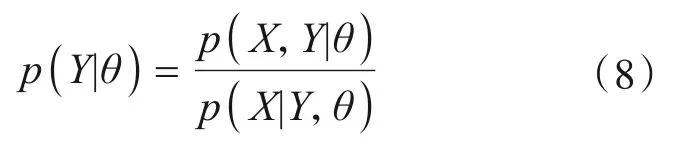
两边同时取对数可得：

由此，EM迭代算法主要分为E步和M步，以此循环迭代，直至满足设定的收敛条件。①E步：计算条件期望Q(θ)；②M步：求函数Q(θ|)的最大值，得到新的估计值。迭代收敛条件为

式中，ρ为目标收敛率。

具体应用EM算法求解随机状态模型式（1）的参数θ的极大似然估计值中，我们可将模型的状态向量{x1，x2，…，xN+1}视为遗漏数据X，离散响应数据Y={y1，y2，…，yN}为已知数据，EM每一步的估计值为［26］

其中，

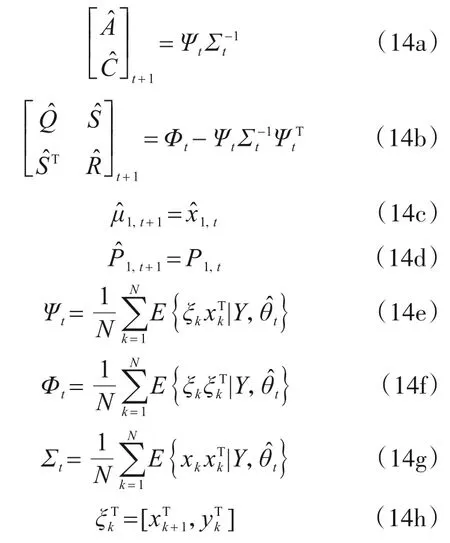
式（14）中所有条件期望可通过卡尔曼滤波和卡尔曼平滑求得［26］。

2 模态参数的不确定性分析

2.1 克拉美罗下界(CRB)

在统计估计理论中，CRB对任何无偏估计量的函数的协方差确定了一个下界，其公式可以表示为［27］

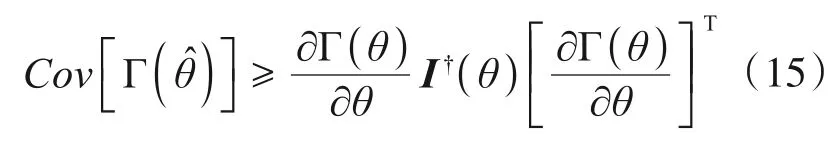
式中，Γ(θ)为所考虑模型参数的函数，如模型参数、模态参数等；为Γ(θ)对θ的雅可比矩阵，†表示矩阵的伪逆；I(θ)表示系统参数化模型的Fisher信息矩阵（FIM），其具体元素可表示为

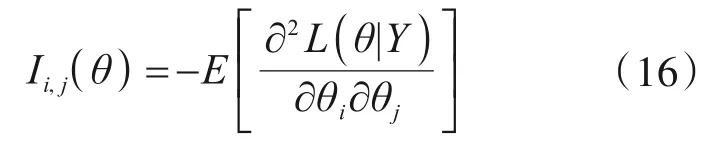
式中，i，j表示FIM的元素位置。

针对随机状态空间模型的似然函数式（6），有［28］

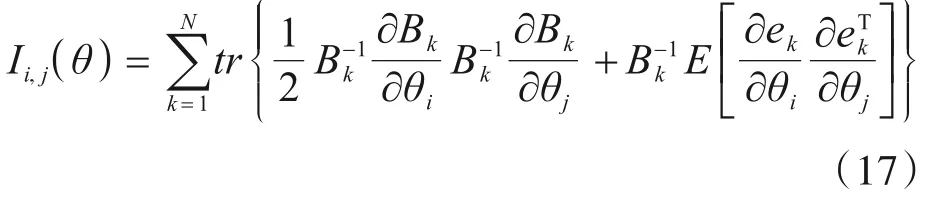
在计算参数的CRB时，其关键在于FIM的计算。但由于FIM的维度一般较大，导致运行时间过长，为了在保证计算精度的情况下缩减运行时间，本文采用了由Shi等［29］提出的快速计算FIM的方法。

2.2 模态形式状态空间方程

由于结构频率和阻尼比只与A的特征值有关，将一般形式的随机状态空间方程转换为模态形式后计算FIM，可直接获得模态参数的协方差信息。对随机状态空间方程式（1）做相似变换，令xk=，可转换为模态形式的状态空间方程：

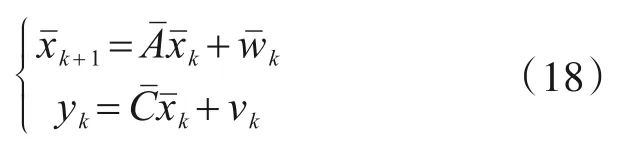
式（19）中每个复模态分块矩阵与结构频率和阻尼的对应关系为

式中：fi，ζi为第i个复模态的频率和阻尼比；Ts为采样步长；j2=-1。

另外，式（18）中模态形式的Cˉ矩阵为一特殊归一化的形式，具体表达式为

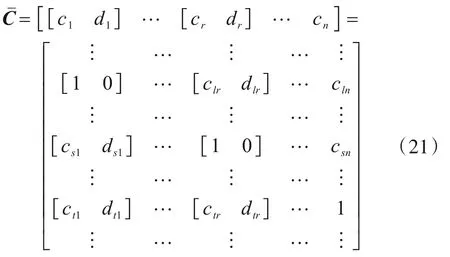
其中，[1 0]或1代表了每一模态振型最大幅值所对应的位置。

相似变换矩阵T可由式（19）和式（21）的模态形式Aˉ和Cˉ反推求得，具体参考文献［29］。

此时，模态形式的状态空间模型式（18）的参数变量可写成

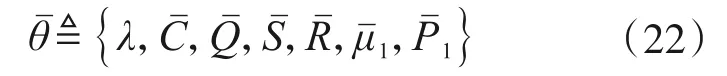
式中，λ=[f1，f2，…，fm，ζ1，ζ2，…，ζm]T为系统的模态频率和阻尼比组成的向量。

2.3 模态参数不确定性的量化

根据模态形式状态空间模型式（18），模态参数中的频率和阻尼比只与系统矩阵有关，而振型只与输出矩阵有关。因此，模态参数函数Γ()与模型参数θˉ的对应关系为

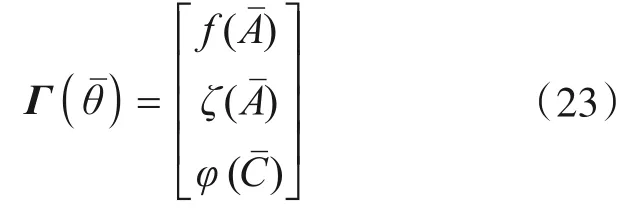
利用式（23）并结合模态形式状态空间模型，然后通过2.1部分的CRB计算，就可以直接求得模态参数的协方差下界。由于极大似然法的渐近无偏估计、渐近一致性和渐近有效性特点，CRB可以用来近似成参数不确定性水平。

本文采用的基于状态空间模型的运行模态及不确定性分析方法的流程图见图1。总的来说，该方法采用随机状态空间（SSI）方法得到状态空间模型参数θ的初值，通过卡尔曼滤波和极大似然估计构建对数似然函数，利用EM迭代算法更新系统参数求得满足收敛条件的极大似然值θ^，从而完成模态参数的识别，并利用CRB界限近似计算参数的不确定性水平，实现了参数不确定性量化。然而，风力机在环境激励下采集的振动信号中，除了含有结构的模态信息外，通常还会存在其他一些虚假模态，比如激励模态、风轮转动的谐波模态以及传感器电子干扰模态等。因此，对振动信号进行本文的模态分析方法识别出的模态信息，需进一步结合结构模态信息的特点，对虚假模态加以去除。

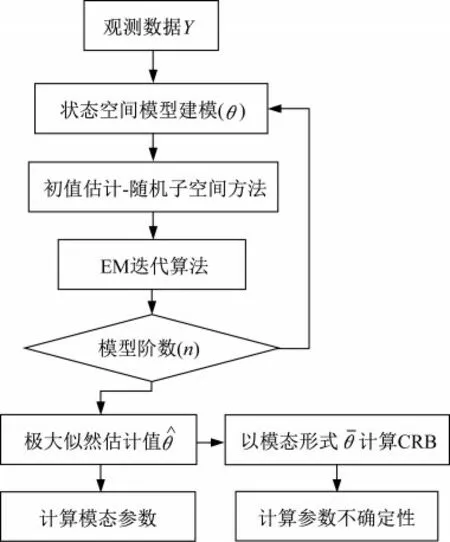
图1 基于状态空间模型的运行模态及不确定性分析方法流程图Fig.1 Flowchart of operating modal analysis and uncertainty quantification based on state-space model

3 应用举例

3.1 风电机组现场实测

实测风力发电机组如图2（a）所示，为Nordex S70 1.5 MW三叶片水平轴风力机，风机轮毂高度65 m，塔架塔底直径4.04 m，塔顶直径2.96 m。采集振动响应的四个单轴压电加速度计安装在塔内的三个维护平台上，详细的安装位置与方向如图2（b）所示。一般认为，垂直于风机扫风平面的方向为塔架的前后方向，平行于风机扫风平面的方向为塔架侧向方向。本次测试的风机停机工况，传感器方向大致与风机塔架主轴振动方向对齐。考虑风电机组两种典型受力工况下，即停机时和正常运行发电时的结构振动响应，实测加速度响应时程如图3所示，采样频率为100 Hz。两种测试工况下振动信号的奇异值（SV）频谱图如图4所示，只截取前5Hz范围展示。

图2 实测风力发电机组和加速度传感器布置Fig.2 Tested wind turbine and layout of acceleration sensors

图3 风机在停机与运行工况下的实测动力响应Fig.3 Measured responses of the tested wind turbine under parked and operating conditions

由文献［22］可知，该风机在停机与运行工况时，其塔架前后方向前两阶模态的频率均在0.5 Hz和4.0 Hz附近［22］。从图3和图4中可以看出，风机运转发电时的振动幅值明显大于停机工况，且两种工况的SV频谱图除了塔架前两阶频率对应的0.5 Hz和4.0 Hz附近有明显的峰值外，其他地方也出现了新的峰值。对于停机工况，1.0～2.0 Hz出现的峰值，这是叶片振动为主对应的模态［30］；而运行工况下出现的新峰值主要对应于风机叶片旋转造成的谐波频率，即以1P（叶片旋转频率），3P，6P，…，3nP等叶片通过频率出现。其中，3P叶片通过频率与塔架的第一阶振动频率接近，这给准确估计风机的模态信息带来了困难。

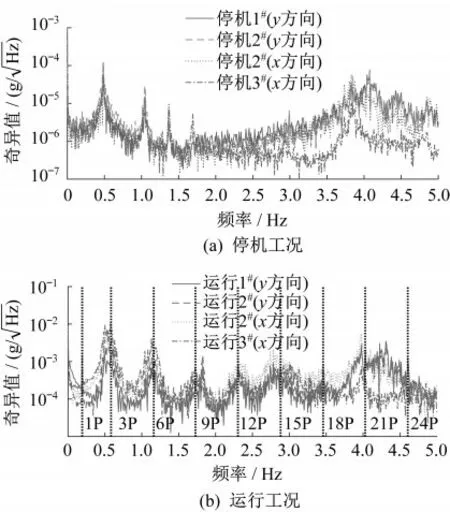
图4 测量动力响应的SV频谱图Fig.4 SV spectrum of measured responses

3.2 滤波处理及初始条件设置

由于所测得的振动响应数据点较多，为提高计算效率，对响应数据先进行滤波处理和重采样。另外，此处还介绍了在使用本文方法时一些初始条件的设置。

由于塔架的前两阶模态在风机结构性能评估中显得更重要，因此本文主要识别塔架两个主轴振动方向的前两阶模态。塔架前两阶频率根据上一节已知在5 Hz以内，而振动信号的原始采样频率为100 Hz，信号范围带宽较大。因此，本文采用低通滤波器对测得的加速度响应先进行滤波，设置的截断频率为5 Hz，然后对滤波数据进行重采样，重采样的频率为10 Hz。

在用随机状态空间模型识别的过程中，模型阶次n的确定也影响该方法的准确性和效率。这里，对状态空间模型阶次通过EM迭代过程来确定。首先，通过查看图4中停机工况与运行工况的峰值数，初步确定一个模型阶次值；其次，通过对残差信息ek进行白噪声验证，如不满足，则通过逐步增加模型阶次的思路；最后，找出合适的阶次值。针对实测风机情况，从图4中可知，风电塔停机与运行工况下SV频谱图中前5Hz范围内分别有9个、12个峰值，即停机与运行工况的初始模型阶次分别取18、24。接着，对识别得到的残差信息ek进行相应的频谱图分析，如若其SV频谱图中有着明显的峰值，则依次增加模型阶次大小，直至其无明显峰值，近似于白噪声在频域中的表现。结果发现，对于停机工况，当n=28时，其残余信息SV频谱图，已无明显峰值存在，可认为接近白噪声，如图5（a）所示；对于运行工况，当n=70时，其残余信息SV频谱图，已经近似于白噪声在频域中的表现，如图5（b）所示。

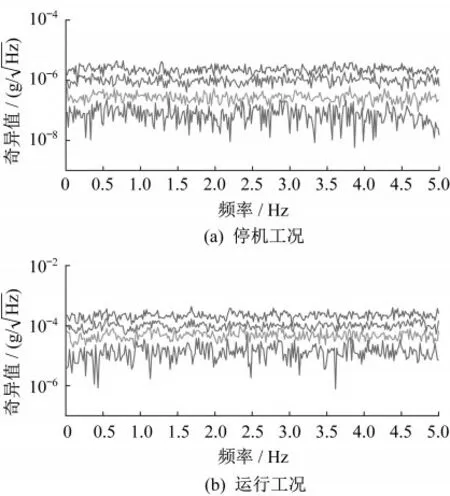
图5 停机和运行工况下残差信息SV频谱图Fig.5 SV spectrum of residuals under parked and operating conditions

通过SSI方法得到的模型参数用作EM算法的迭代初值，然后对似然函数进行多次迭代。尽管理论上，迭代次数越多，其识别结果越精准，但这也将加大线下处理时间。采用目标收敛率ρ=1.0×10-5时，两种工况下的EM迭代过程如图6所示。

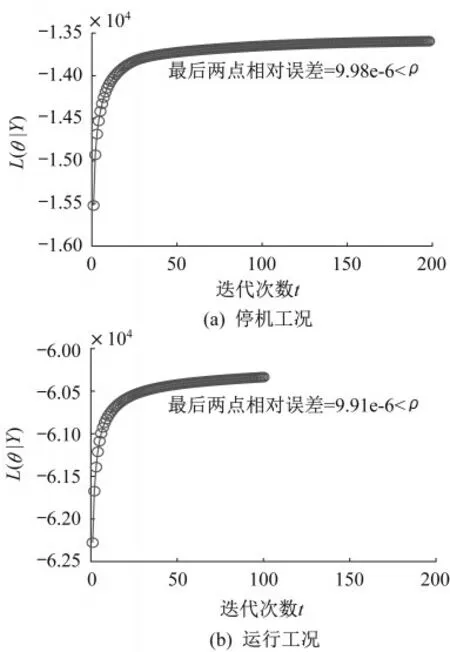
图6 EM算法迭代曲线图（目标收敛率ρ=1.0×10-5）Fig.6 EM iteration process（target convergence rate ρ=1.0×10-5）

3.3 模态分析结果

根据上节的滤波处理以及初始条件设置，即可对测得的加速度响应进行模态参数识别，然后再应用CRB界限近似计算模态参数的不确定性水平。

考虑到在停机工况下传感器布置方向与塔架主轴方向基本一致，原先为了快速比较两个方向模态参数的差异性，将测得的x方向两条响应数据与y方向的数据分开分别进行模态参数识别（分开识别）。但考虑到风机塔架为一整体结构，其x方向与y方向必然存在着耦合作用，且参数识别时使用的加速度响应越多，其识别结果越精确，因此又将停机工况测得的四条加速度响应放在一起进行模态识别（一起识别），并将两种识别方式结果进行了比较。表1和表2列出了上述两种识别情况的模态参数和不确定性结果。从表1和表2可知，两种方式识别出的前两阶频率和阻尼比虽存在一些差异，但数值比较接近。这说明停机时的传感器布置方向是与塔架振动方向比较一致的，这种情况下分开识别和一起识别对模态参数的估计值影响不大。然而，通过比较这两种情况的不确定性水平，可以看出一起识别的模态参数变异系数大部分小于分开识别的，尤其表现在阻尼比方面。这也说明了将四条停机数据放在一起，包含了更多的振动信息，必然有助于识别的准确性。同时，特别随着风向改变，风机对风轮转动后风机工作，造成传感器方向与塔架振动方向不一致，需要所有振动信号放在一起识别，并结合振型才能准确确定风机实际的前后振动与侧向振动模态。因此，风机模态识别结果应采用一起识别的方式识别的为准。

表1 停机工况下分开识别的模态参数及不确定性Table 1 Modal parameters and uncertainties identified separately under parked condition

根据表2的停机工况识别结果可知，风机停机工况下，塔架侧向的前两阶频率0.49 Hz和4.07 Hz均大于前后方向0.48 Hz和3.83 Hz，且第二阶频率的差异更明显。侧向的前两阶阻尼比2.37%和0.98%同样均大于前后方向0.65%和0.72%，且第一阶阻尼比的差异更明显。风机塔架振动为主的不同方向的模态阻尼比的不同，主要与叶片桨距角有关。受空气动力阻尼的影响，叶片拍打振动方向的阻尼比往往比挥舞振动方向的阻尼比大一些。另外，从前两阶模态参数对应的变异系数可知，阻尼比的不确定性远大于频率，这也符合一般模态分析的现象。

表2 停机工况下一起识别的模态参数及不确定性Table 2 Modal parameters and uncertainties identified together under parked condition

风机运行工况下的识别结果如表3所示，可以发现风机风轮转动的情况下，塔架前后方向的第一阶频率0.50 Hz略大于侧向的0.49 Hz。此时，前后方向的第一阶阻尼比为2.27%，也高于侧向的0.53%。这也符合之前停机时的结论，因为风机运行时桨距角调整是叶片对风，叶片拍打方向转变为塔身前后方向，所以受气动阻尼影响，前后方向的一阶阻尼比偏大。而对于塔架的第二阶模态，从表中可以看出，运行工况下，风电塔前后方向的第二阶频率3.97 Hz，低于侧边方向4.19 Hz，与停机工况下识别出的第二阶频率情况相似。同样，从前两阶模态参数对应的变异系数都非常小可知，风机运行模态分析的结果具有较好的准确性。

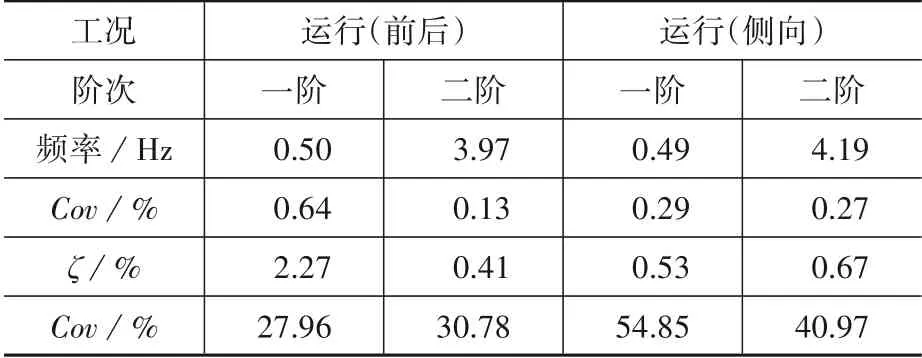
表3 运行工况下一起识别的模态参数及不确定性Table 3 Modal parameters and uncertainties identified together under operating condition

总的来说，比较表2和表3风机停机与运行工况的模态参数结果，可以看出同一工况下风机塔架的前后与侧向模态参数的确存在着差异性。风机运行工况下模态频率均比对应的停机工况的结果要大，这是由于风叶转动时产生了巨大的惯性力，导致风机的有效质量减少、叶片的刚度增大，使其整体刚度增大，根据刚度与频率的关系可知，其频率也会增大。对于运行工况下的塔身前后方向第一阶阻尼比2.27%远大于停机工况下的0.65%，以及对于停机工况下塔身侧向的第一阶阻尼比2.37%远大于运行工况的0.53%，这是因为气动阻尼主要影响叶片拍打方向的模态导致的［31］。

4 结论

本文介绍了一种基于状态空间模型的运行模态及不确定性分析的方法。通过卡尔曼滤波构建模型参数的似然函数，利用EM迭代算法更新模型参数求其极大似然值，进而估计模态参数，并利用CRB界限近似计算参数的不确定性水平，实现参数不确定性量化。在大型风力机带有旋转叶片谐波影响的运行模态分析中，此方法可有效解决模态参数识别困难的问题，并得到模态参数估计的不确定性水平，为后续决策提供科学依据。本文提出的针对叶片旋转的风机运行模态分析方法，适用于叶片基本是正常匀速转动的条件下，不适用于启停阶段或叶片转速变化大的运行时段。另外，不同风况下风机自身的控制策略会调节风机正常运行的叶片匀速转动的速度，不影响本文方法的应用，但是由于气动阻尼与结构振动的幅度和速度有关，因此不同风况下结构的气动阻尼会受到影响。通过实际大型风力机在停机和运行两种工况的模态分析，着重分析了风机塔架不同方向模态参数的差异性，以及不同工况下模态参数及不确定性的变化。分析结果表明：

（1）风机叶片为细柔不对称构件，气动阻尼影响明显，且气动阻尼主要影响叶片拍打方向的塔架第一阶模态阻尼；

（2）由于风轮转动的影响，风机运行工况下的模态频率略大于对应的停机工况下的模态频率；

（3）无论风机是在停机还是运行工况下，塔架侧向振动方向的第二阶模态频率一般大于塔架前后振动方向的第二阶模态频率。