重庆山地区域气象要素空间插值方法对比

杨春华 郑莉 黄河清 雷波 杨硕 刘建辉 张明阳 段秋宴

（1.重庆市生态环境科学研究院，重庆 401147；2.重庆市第八中学，重庆 400030；3.中国科学院亚热带农业生态研究所，湖南 长沙 410125；4.重庆市渝北区生态环境监测站，重庆 401120）

引言

气象数据广泛应用于气象、环境、农业、林业等诸多领域［1-4］，离散气象观测数据的空间化是其得以应用的关键［5-9］。获取空间化气象要素，一般可利用卫星遥感数据反演和空间插值等手段。卫星遥感数据反演能获取空间分辨率较高的气象要素，但当前仅能获取部分气象要素，且只能获取卫星过境时刻的数据［10］，因此通过空间插值获取空间化气象数据仍是当前比较主流的方法之一。气象观测资料作为一种空间数据，蕴含着复杂的非线性动力学机制，在时空分布上具有纷杂多变的时空特征［11］，因此气象数据空间插值方法一直是研究的热点［12-13］。

气象要素空间插值目前已有一系列方法，主要可归纳为整体插值法、局部插值法、混合插值法（整体插值法和局部插值法综合）3类［14-15］。一般多采用局部拟合方法，即用邻近未知点的少数已知样点的特征值来估算该未知点的特征值，只考虑内插区域的局部特性而不受其他区域的影响［16］。众多插值方法中，基于地质统计技术的克里金法和薄盘光滑样条函数法较为通用，这些技术建模只将空间分布作为观测数据的函数而不需要先验知识和物理过程，能提高插值准确度［17-20］。然而大量研究表明，不同插值方法存在各自的优劣［21-25］，气象要素变化十分复杂，区域内不同插值方法结果会有较大区别［12］，同一插值方法在不同区域也会表现出不同差异。因此，并不存在一种插值方法适用于所有气象要素，应根据特定的环境区域选取适宜的插值方法及参数［26-29］。

重庆地处大巴山断褶带、川东褶皱带和川湘黔隆起褶皱带三大构造单元交汇处的山区，周边区域海拔为5—3064 m，地形起伏大，地貌类型复杂多样。该区域地形大势由南北向长江河谷倾斜，东北部、东部、南部为大巴山山地、巫山山地、武陵山地、大娄山余脉构成的盆周中低山区，中北部为平行岭谷区，西部为川中丘陵区。区域内陡峻的山地和复杂多变的自然环境，使之成为第四纪冰川时期生物的优良避难地，珍稀濒危和中国特有动植物物种极为丰富，尤其渝东北和渝东南更是位于中国17个具有全球意义的生物多样性保护关键区域内。大巴山、武陵山两个生物多样性优先保护区和举世闻名的三峡库区均位于此，是长江上游重要生态屏障。特殊山地环境决定了气象要素空间分布的显著异质性，加之生态地位突出而独特，因此对其开展深入研究尤为重要。

本研究在重庆及周边山地区域3.615×105km2的空间范围，主要考虑高程因素，采用薄盘光滑样条函数法、反距离加权法、普通克里金和协同克里金4种常用方法，分别从年、月两种尺度对气温、降水和太阳总辐射三个气象要素进行空间插值，以期对比分析复杂地形地貌条件下空间数据最优插值方法，为重庆山地区域生态环境动态变化研究和提升区域生态评估精度提供科学参考。

1 资料与方法

1.1 数据来源与处理

重庆区域水热条件好、年际变化不明显，因此选取1999年、2018年较长时间间隔气象数据，研究正常、自然年份下插值方法的适用性。两个年份月值气象数据来自于国家气象信息中心和重庆市气象局，其中气温和降水要素1999年有163个国家气象站点（图1），2018年区域站点加密后共285个站点。太阳总辐射要素来源于国家气象信息中心“中国国家地面站太阳总辐射估算值数据集（V1.0）”，1999年和2018年站点数分别为162个、165个。利用月值数据获取年均温、年降水量、年太阳总辐射，运用ANUSPLIN软件先将气象数据通过SPSS软件处理成标准ASCII格式。高程数据来源于CGIAR-CSI SRTM中国区域数据（http：//srtm.csi.cgiar.org/），首先在GIS软件中对其进行拼接、裁剪，然后将其重采样为250 m，投影转换为UTMZONE48，最后将其转成ASCII格式作为协变量参与插值。

图1 研究区高程及1999年气象站点分布Fig.1 Elevation and distribution ofmeteorological stations w ithin the studied region

1.2 空间插值方法

1.2.1ANUSPLIN（ANUS）

澳大利亚科学家Hutchinson基于薄盘样条理论编写了针对气候数据曲面拟合的专用软件ANUSPLIN［30-31］，它允许引进多元协变量线性子模型，自动确定模型系数，可平稳处理二维以上的样条，可引入多个影响因子作为协变量［32］。其理论模型公式为

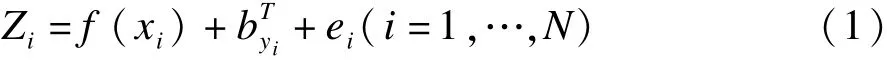
式（1）中，Zi为空间i处待插值点气象要素值；xi为d维样条的独立变量，是位置i处周边已知站点气象要素值；f为关于xi的未知光滑函数；yi为独立协变量（本研究为高程）；b为独立协变量系数；ei为随机误差。

光滑函数f和系数b利用控制点求得，将Zi设置在控制点上，根据周边其他已知控制点插值该点，通过最小二乘来确定

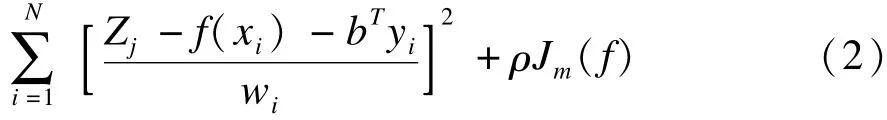
式（2）中，Jm（f）是函数f（xi）的粗糙度测度函数，定义为函数f的m阶偏导（Anus称样条次数）；ρ是正的光滑参数，在数据保真度与曲面粗糙度之间起平衡作用，通常由广义交叉验证GCV（Generalized cross validation）最小化来确定，也可用最大似然法GML（Generalised max likelood）或期望真实平方误差MSE（expected true square error）最小化确定［31，33］。

本方法各气象要素均以DEM作为协变量，根据GCV最小和Signal小于观测站点一半的原则选取最优模型。通过对样条次数从2—6分别尝试，样条次数取3时，GCV最小，因此本研究样条次数取3。考虑到降水随机性强且值域范围大的特点，对原始数据进行平方根变换降低数据值域范围［33］，太阳总辐射也参照降水进行平方根变换。

1.2.2反距离加权（Inverse DistanceWeighted，IDW）

IDW由Shepard最早提出并发展起来［34］，其估计值由研究区内样本点实测值加权决定，而权重由距离决定，样本点离待插点越近影响越大，反之越小。公式为［15］

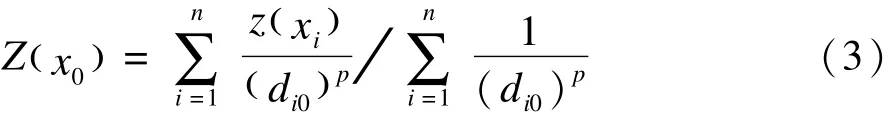
式（3）中，Z（x0）为x0处预测值；z（xi）为xi处观测值；n为预测中使用的周围站点数；di0为预测点x0与各已知样点xi间距离；p为距离的幂次数。

IDW插值中距离的幂次数和搜索范围一般均取默认值2和12，同时为便于与其他研究成果比较［15］，本研究取默认值。

1.2.3普通克里金（Ordinary Kriging，OK）

OK是利用区域化变量的原始数据和变异函数的结构特点，对未知样点进行线性无偏、最优估计的一种方法［35］。计算公式为

式（4）中，Z（x0）为未知点预测值；Z（xi）为未知点周围气象站点观测值；ω为第i个已知站点对未知点的权重；N为已知气象站点数量。

赋权重时OK不仅考虑距离，而且通过变异函数和结构分析，考虑已知样本点的空间分布及与未知样本点的空间方位关系［36］。ArcGIS软件中OK半变异函数取默认值球面模型，搜索半径取可变方式下的默认值12，为便于比较，本研究跟大多数研究一样取此默认值。

1.2.4协同克里金（Co-Kriging，CK）

CK基本原理同OK，但它把区域化变量的最佳估值方法从单一属性发展到二个以上的协同区域化属性。温度、降水等要素经常受海拔影响，本研究将海拔作为第二属性引入。公式表示为［15］

式（5）中，Z（x0）为x0点预测值；Z（xi）为第i站点测量值；y（x0）为x0点高程；N为已知气象站点个数；mY、mZ为高程和气象数据的全局平均值；ω、σ为协同克里金插值权重系数。

为便于与OK比较，选择默认球面模型作为变异函数理论模型，搜索范围同样取默认值12，即预测点邻近的12个站点。

1.3 结果检验

采用交叉验证方法对预测结果进行对比分析，将原始样本数据集分为两部分：一部分作为“训练集”，另一部分作为“验证集”［13］。用训练集样本进行全范围插值，将插值结果与“验证集”站点（不参与插值）观测数据对比。插值站点数量越多，插值结果精度越高［37］，因此本研究将总样本数的90%用于“训练”，10%用于“验证”。验证站点设置以空间分布均匀性为主，同时考虑海拔（图1）。使用平均绝对误差（Mean Absolute Error，MAE）、平均相对误差（Magnitude of Relative Error，MRE）和均方根误差（Root Mean Square Error，RMSE）作为插值结果检验标准。MAE估算估计值可能的误差范围，MRE反映估计误差相对于观测数据的大小，RMSE反映利用样点（气象台站）数据的估值灵敏度和极值效应［38］。表达式分别为

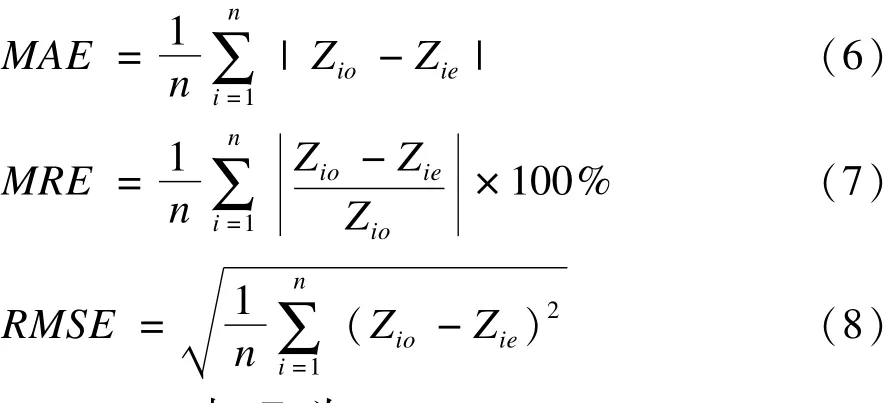
式（6）—式（7）中，Zio为第i站点观测值；Zie为第i站点估计值；n为“验证集”点位数。

2 结果分析

2.1 气温

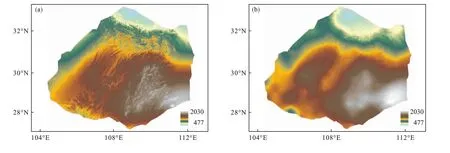
研究区1999年平均气温四种方法插值结果见图2。从目视效果看，四种插值结果在空间分布上大体一致，总体均呈现出气温在北部及中部、西南角落低，其余高的趋势。ANUS因有高程作为协变量，结果与DEM表现出较高一致性，可反映复杂地形下温度的空间差异；CK也考虑了DEM，但“组团”现象明显且结果不如ANUS细腻；OK未考虑其他因子，结果表现出“鱼鳞”斑块状，因OK利用周围已知点，结合半方差分析建立统计模型，在站点少且气象要素空间异质性大的区域容易产生这种现象；IDW明显出现因高温或低温形成的“牛眼”现象。2018年空间分布规律（图略）与1999年总体一致，但因站点数量更多，空间异质性增大，“牛眼”现象更明显。

年尺度上，1999年和2018年年均气温MAE、MRE、RMSE均以ANUS最优（表1）。月尺度上ANUS优势同样明显，MAE（℃）月均值1999年为ANUS（0.37）＜IDW（0.55）＜CK（0.58）＜OK（0.61），2018年为ANUS（0.43）＜IDW（0.74）＜CK（0.80）＜OK（0.87）；MRE（%）月均值1999年为ANUS（2.79）＜IDW（3.92）＜CK（4.07）＜OK（4.23），2018年为ANUS（3.20）＜IDW（5.83）＜CK（6.32）＜OK（6.69）；RMSE（℃）月均值1999年为ANUS（0.45）＜IDW（0.93）＜CK（0.95）＜OK（0.97），2018年为ANUS（0.52）＜IDW（0.97）＜CK（1.05）＜OK（1.08）。各月MAE、MRE、RMSE均以ANUS最小，其他为IDW＜CK＜OK但差别不大（表略）。不同时间尺度以及年内不同月份间观测值均差异较大，MAE和RMSE缺乏可比性，因此用MRE比较不同尺度插值效果（降雨和太阳总辐射，下同）。两年中最高气温均出现在5—9月，此时MRE全年最小（MAE和RMSE处于最大），表明低气温月份插值结果误差更大。四种方法1999年MRE月均值为3%—4%，平均3.75%，年尺度MRE在3%左右，平均3.03%；2018年MRE月均值为3%—7%，平均5.51%，年尺度MRE为2%—5%，平均3.68%。四种方法均表现出插值精度年尺度优于月尺度，因此，本研究区时间尺度越小插值误差越大。

综上，研究区气温最优插值方法为ANUS。通过ANUS，气温1999年的月、年尺度平均MRE分别为2.79%、1.86%，2018年分别为3.20%、2.03%。

图2 1999年研究区年均气温ANUS（a）、CK（b）、OK（c）和IDW（d）插值结果Fig.2 Interpolation results of annual average air temperature based on methods of ANUS（a），CK（b），OK（c），and IDW（d）in the studied area in 1999

表1 研究区年均气温不同插值方法对比Table 1 Comparison of different interpolation methods for annual average air tem perature in the studied area

2.2 降水

从目视效果看，研究区降水量1999年四种插值结果在空间分布上大体一致，都呈现出降水量北部区域低、其余尤其是东南缘高的分布趋势（图3）。因降水值域范围跨度大，显示效果上OK“鱼鳞”效应和IDW“牛眼”现象均有所减弱。2018年降水量空间分布规律（图略）与1999年基本一致，但站点数量更多，异质性增大，“鱼鳞”和“牛眼”现象更明显。

年尺度上1999和2018年降水量MAE、MRE、RMSE均以IDW最优，考虑了DEM的ANUS和CK并未显示出优越性（表2）。

月尺度上，四种方法MRE、MAE、RMSE变化规律与年尺度不尽相同（图4）。

四种方法MAE（mm）月均值1999年为IDW（16.96）＜CK（17.46）＜ANUS（18.04）＜OK（18.26），2018年为IDW（19.88）＜CK（20.80）＜ANUS（21.63）＝OK（21.63）；MRE（%）1999年为CK（16.78）＜ANUS（17.24）＜IDW（17.42）＜OK（18.87），2018年为IDW（23.14）＜CK（23.82）＜ANUS（24.00）＜OK（24.74）；RMSE（mm）1999年为IDW（20.76）＜CK（21.80）＜ANUS（22.36）≈OK（22.38），2018年为IDW（26.41）＜CK（27.52）＜OK（28.78）＜ANUS（29.83）。图4直观反映出IDW各月MAE、MRE、RMSE整体最低，总体效果最好。

图3 1999年研究区累积降水ANUS（a）、CK（b）、OK（c）和IDW（d）插值结果Fig.3 Interpolation results of cumulative precipitation based on methods of ANUS（a），CK（b），OK（c），and IDW（d）in the studied area in 1999

表2 研究区年均累积降水量不同插值方法对比Table 2 Com parison of different interpolation methods for annualmean cumulative precipitation in the studied area

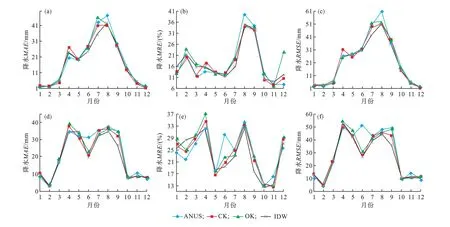
图4 1999年逐月降水MAE（a）、MRE（b）、RSME（c）和2018年逐月降水MAE（d）、MRE（e）、RSME（f）各月累积降水不同插值方法对比Fig.4 Com parison of MAE（a），MRE（b），and RSME（c）ofmonthly cumulative precipitation using different interpolation methods in 1999 and in 2018（d-f）

四种方法各种误差在不同月份变化趋势基本一致，两年中4—9月降水量多时，MRE总体高于其他月份（MAE、RMSE更明显），表明多降水月份插值结果误差更大。1999年四种方法的MRE月均值为17%左右，平均17.58%，年尺度MRE为7.00%左右，平均7.41%；2018年MRE月均值为23%左右，平均23.93%，年尺度MRE在12%左右，平均11.75%（图4）。以上表明，四种方法均表现出降水插值精度年尺度优于月尺度，时间尺度越小误差越大。

综上，研究区降水最优插值方法为IDW。通过IDW，1999年降水的月、年尺度平均MRE分别为17.42%、6.87%，2018年分别为23.14%、11.20%。

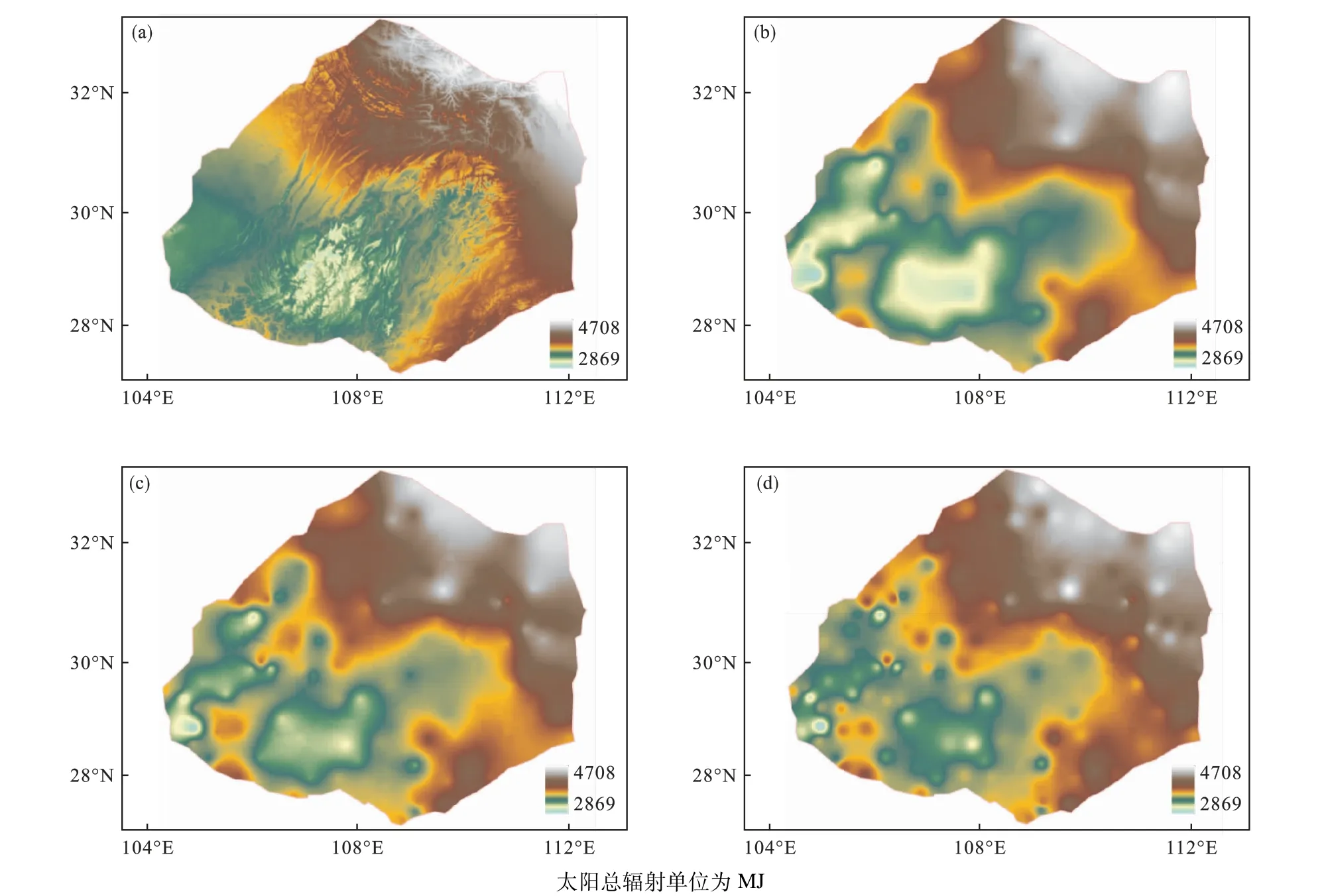
图5 1999年研究区太阳总辐射ANUS（a）、CK（b）、OK（c）和IDW（d）插值结果Fig.5 Interpolation results of total solar radiation based on methods of ANUS（a），CK（b），OK（c），and IDW（d）in the studied area in 1999

2.3 太阳总辐射

从目视效果看，研究区1999年四种插值结果空间分布上总体一致，太阳总辐射均呈西南及中部区域低，其余为东北缘高的分布趋势（图5）。太阳总辐射值域跨度较大，OK“鱼鳞”效应和IDW“牛眼”现象均有所减弱。2018年空间分布规律（图略）与1999年基本一致，站点数量一致使得“鱼鳞”和“牛眼”现象也基本一致。

表3 研究区年均太阳总辐射不同插值方法对比Table 3 Com parison of different interpolation methods for annualmean total solar radiation in the studied area

年尺度下，两个年份太阳总辐射误差变化更加复杂，1999年3种误差以IDW全面占优，2018年以ANUS占优为主（表3）。月尺度上，四种方法MAE、MRE、RMSE变化规律与年尺度基本一致。MAE（MJ）月 均 值1999年 为IDW（16.28）＜OK（16.49）≈CK（16.54）＜ANUS（17.05），2018年为ANUS（14.85）＜CK（16.08）＜IDW（16.34）＜OK（16.51）；MRE（%）月均值1999年为IDW（5.45）＜ANUS（5.82）＜OK（5.63）≈CK（5.65），2018年为ANUS（4.88）＜CK（5.27）≈IDW（5.29）≈OK（5.34）；RMSE（MJ）月均值1999年为IDW（20.77）＜CK（21.02）≈OK（21.05）＜ANUS（21.45），2018年为ANUS（18.44）＜CK（19.42）＜IDW（19.87）＜OK（20.13）。

不同月份四种方法的各种误差波动趋势基本一致（图6）。1999年6—9月和2018年5—8月太阳总辐射较高，其MRE总体上位于全年最低（MAE、RMSE全年最大），全年太阳总辐射最低时（1月、2月、11月、12月）MRE最大，表明太阳总辐射值小的月份插值结果误差更大。四种方法1999年太阳总辐射MRE月均值为5%—6%，平均5.64%；年尺度MRE为4%—5%，平均4.60%。2018年MRE月均值5%左右，平均5.19%；年尺度MRE为3%—4%，平均3.38%。四种方法插值精度均表现为年尺度优于月尺度，表明研究区时间尺度越小结果误差越大。

研究区2018年太阳总辐射最优插值方法的年、月尺度基本均为ANUS，1999年虽为IDW，但值得注意的是四种方法差异极小。1999年月均值变化幅度MAE仅0.76 MJ、MRE仅0.37%、RMSE仅0.69 MJ（图6），因此从误差角度四种方法均可采用。但利用ANUS还可提供空间分布标准差、协变量误差等一系列参数辅助判断空间插值可靠性［10］，更重要的是它能同时对多个表面进行插值，尤其适合时间序列的气象数据［32］，因此ANUS逐步成为空间插值的主要工具之一，越来越多地应用于山区［39］。

综上，本研究太阳总辐射最优插值模型采用ANUS方法。通过ANUS，太阳总辐射1999年的月、年尺度平均MRE分别为5.82%、4.60%，2018年分别为4.88%、3.03%。

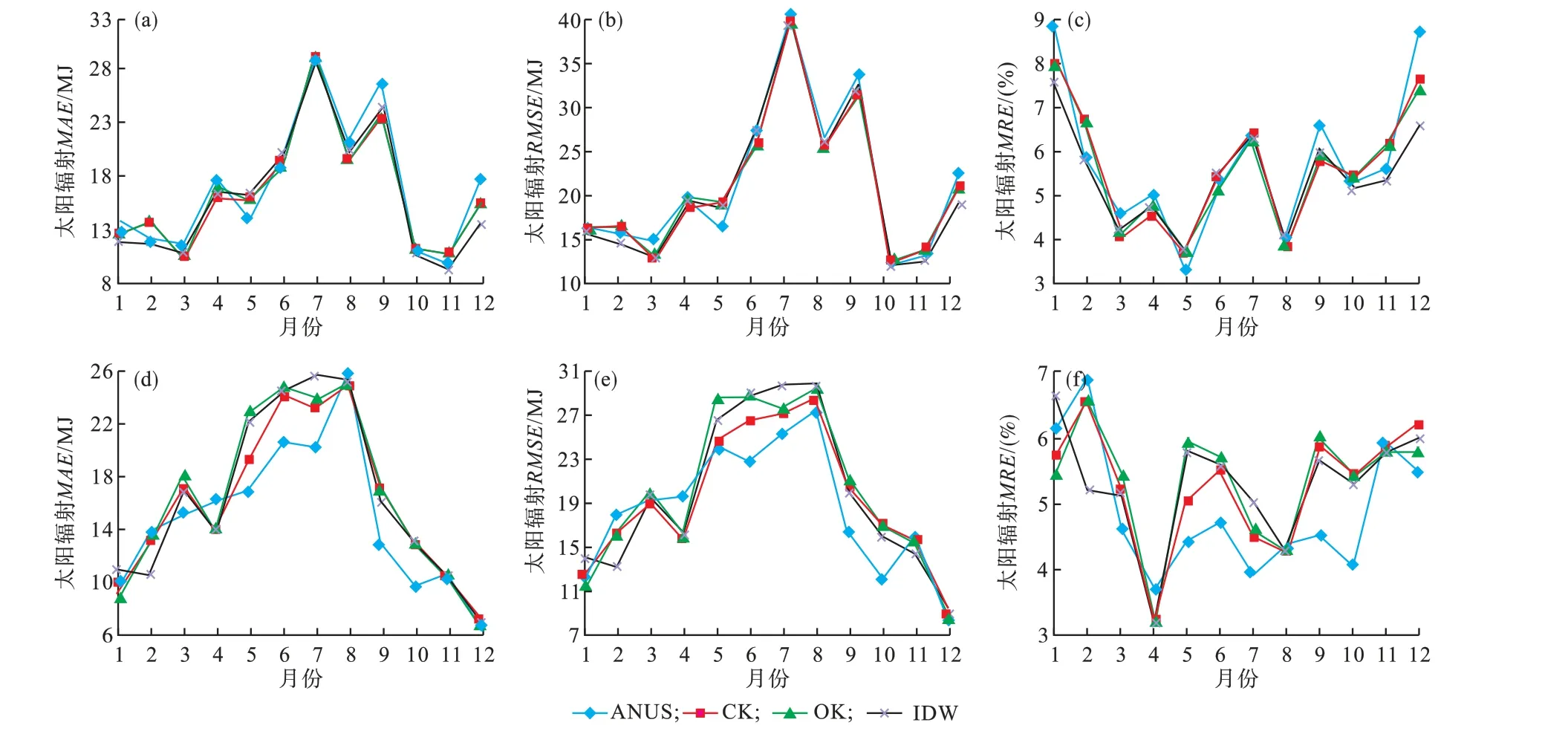
图6 1999年研究区太阳总辐射MAE（a）、RMSE（b）、MRE（c）和2018年太阳总辐射MAE（d）、RSME（e）、MRE（f）不同插值方法对比Fig.6 Comparison of MAE（a），MRE（b），and RSME（c）ofmonthly total solar radiation using different interpolation methods in 1999 and in 2018（d-f）

3 结论与讨论

（1）1999年和2018年重庆山地区域三个要素插值误差气温较小，太阳总辐射其次，降水量较大。三个要素插值精度均为年尺度优于月尺度，但月尺度上气温和太阳总辐射精度在高值月份优于低值月份，降水相反。气温和太阳总辐射最优插值方法均为ANUS。该方法下气温1999年和2018年月均MRE分别为2.79%、3.2%，年尺度MRE分别为1.86%、2.03%；太阳总辐射1999年和2018年月均MRE分别为5.82%、4.88%，年尺度MRE分别为4.6%、3.03%。降水最优插值方法为IDW，该方法下1999年和2018年月均MRE分别为17.42%、23.14%，年尺度MRE分别为6.87%、11.20%。

（2）由于气象因素较复杂，插值精度多受插值范围和插值方法的影响，插值方法的影响较为常见。任璇等［12］在新疆用90个站点7月平均降水量为指标进行插值时，发现ANUS精度比CK提高了46.78%，比IDW提高了56.77%；插值范围即采用比研究区更大范围内的气象观测数据通常可提升精度。谭剑波等［10］通过ANUS利用2010年96个气象站点对青藏高原东南缘1.1646×106km2范围插值时年降水和年均温MRE分别为18%、4%，本研究区与青藏高原东南缘地理、气象条件相似，主要差别是比谭剑波等［10］研究的外延范围更大，利用1999年163个气象站点在3.615×105km2范围插值时，年降水和年均温MRE分别达7.67%、1.86%，精度提升明显。可见，引入比研究区更大范围的气象观测数据是一种提升插值精度的有效方法。

（3）本研究气温和太阳总辐射的最优插值方法为ANUS，降水为IDW。究其原因，气温影响因素较多，以海拔和地形影响最显著［40］，太阳总辐射在山区受地形起伏的影响显著，占比可达20%—30%［41］。ANUS对气温和太阳总辐射插值时均将DEM作为协变量，加之自身特殊的模拟算法，因而插值结果表现最优。降水空间异质性更明显，不确定性更大［42］，一方面，降水随机性较大，不同方法插值结果均不尽理想［33］；另一方面，降水与海拔关系复杂且不稳定，部分区域两者存在一定相关性［43］，部分区域却无明显关系［44］。本研究ANUS和CK均引入DEM，但结果精度并无优势，表明本区域海拔因素对降水相关性不强，因此不考虑地形因素的IDW，结果反而表现更优。

（4）2018年较1999年多用了108个重庆区域站加密，结果表明加密后站点密度效应对气温和降水的响应程度差异较大。气温对密度效应响应微弱，年尺度上呈微弱正效应，MRE仅增加0.3%，月尺度上呈微弱负效应，月均MRE仅降低了0.2%。降水对密度效应的响应相对明显且均为负效应，年、月尺度MRE降幅分别达3.12%、4.68%。这与郑小波等［45］在西南山地研究结果一致，即用于插值的台站相对过多时，不一定会提高降水插值精度，这与复杂山地降水场空间分布的连续性较差有关；彭红兰等［46］在三江源地区的研究也表明，对数据来源不一致的站点，数据质量控制不好会大大降低插值精度。重庆共有区域站2000余个，本次研究仅从监测数据是否异常、缺测等数据“可用性”方面选用了108个区域站，未从空间位置、海拔、坡向等对降水影响较大的因素综合选取，加之降水事件自身随机性大，引入重庆区域站可能导致精度下降。因此充分考虑数据自身质量，如何从影响降水的多个因素综合选取区域站是其今后能否得到充分利用的关键。