基于机器学习方法的辽宁省初霜冻日期预测模型研究

王涛 王乙舒 赵春雨 王小桃 秦美欧 沈玉敏 侯依玲 赵建云

（1.沈阳区域气候中心，辽宁 沈阳 110166；2.中国气象局沈阳大气环境研究所，辽宁 沈阳 110166）

引言

霜冻是辽宁省秋季农业生产的主要灾害之一，初霜冻来的早的年份，低温冷害作物成熟期缩短，作物不能安全成熟，遭受冻害，影响粮食产量和质量［1］。因此，初霜冻日期的预测对保证粮食安全具有十分重要意义。

近年来，中国学者在霜冻灾害方面做了大量工作，大多是利用传统统计方法分析初霜冻［2-3］、终霜冻［4-5］、霜冻日［6］气候变化特征、成因［7-8］及对农业生产影响。如王国复等［7］利用1954—2003年中国霜期观测数据，通过趋势分析方法发现中国大部分地区初霜冻日呈推迟趋势而终霜冻日呈提前趋势，并指出日最低气温、日最低0 cm地面温度的升高可能是引起霜冻日期变化的原因。韩荣青等［9］不但分析了中国北方地区初霜冻日期历史变化特征，还讨论了初霜冻日期出现早晚对水稻和玉米产量的影响，发现成熟期之前无持续性异常低温时段，初霜冻日期早晚对其影响是显著的。然而传统统计预测方法也存在很多问题，如特别依赖预报员个人预报经验，预测准确率也不稳定，无法满足当前预测业务发展需求。因此也有少部分学者对客观化初霜冻预报方法进行研究，但大都是从初霜发生前1—3 d大气环流变化去分析研究做出短期预判［10-11］，或者从前期月季环流因子、终霜日、夏季平均气温等因子构建预测模型作出长期预判［12］，其中短期预判由于预测时效较短，农业部门来不及采用大范围防范措施，仍然可以造成较大损失；而长期预测多采用前期比较单一物理指标作为预测因子，通常以线性方法作为主要研究方法，但由于气候变化的非线性特征、预报量与预报因子关系的非线性特征，线性方法的局限性较大。机器学习算法不但可以捕捉前期预测因子作用预测结果的潜在非线性机制，还能提取重要关键预测因子。因此已有学者开始将其应用于预报实践，在预测中表现出良好的效果［13-15］。Moon和Kim［16］基于机器学习中相关性的特征选择来组合短期天气预报中可用的大量气象要素变量的有效子集，从中获得多项式回归的系数，然后将其用于预测降水。孙全德等［17］基于机器学习算法建立预测模型对ECMWF模式预测的中国华北地区10 m风速进行订正，发现机器学习算法的订正效果好于传统订正方法。

目前，机器学习方法应用大都在短临尺度上对模式输出要素做订正评估，缺乏直接在气候尺度上利用前期再分析数据构建预测模型研究，因此本文基于前期ERA5逐月再分析数据（1961—2019年2—7月），采用3种典型机器学习算法（Lasso回归、随机森林和神经网络）建立辽宁省初霜冻日期预测模型。首先基于前期ERA5再分析数据的气象要素特征进行特征选择，即通过特征工程方法提取重要要素特征集，再以筛选出的特征集进行机器学习建模，分别对2—7月起报的辽宁省初霜冻日期进行预测，并检验其效果，最后重点讨论前期因子影响预测结果可能原因，为初霜期预测提供参考。

1 资料与方法

1.1 资料来源

采用的资料分为格点和站点数据，其中格点数据源于欧洲中期预报中心（The fifth generation ECMWF reanalysis for the global climate and weather，ERA5）网站公开的再分析数据，时间段为1961—2019年2—7月，空间范围为115°—130°E，35°—45°N，空间分辨率为0.25°×0.25°，包括对初霜冻日期预测可能有影响的28个气象要素场，在气候预测中优先考虑环流场对当月气温和降水的影响，如当高空为低槽或冷涡（脊或高压）时，有利于当月气温偏低（偏高）、降水偏多（偏少）。植被覆盖、积雪、土壤温度、含水量等要素可能影响当月及秋冬季的局地气温和地面湿度，如植被覆盖率越高越有利于保持地表温度和湿度（具体分析见2.4节）。低温、气温和湿度均为对初霜冻预测可能有影响的因子（表1）。站点数据来自辽宁省气象信息中心，要素为1961—2019年辽宁省61个气象观测站逐年初霜冻日期。

本研究采用研究时段内气象观测站初霜冻日期作为机器学习算法的预测标记，将所在月的28个气象要素场形成的特征矩阵作为输入，经过特征工程，选取有效气象要素构建机器学习初霜期预测模型。

1.2 研究方法

1.2.1Lasso回归

Lasso（Least absolute shrinkage and selection operator）方法是以缩小特征集（降阶）为思想的压缩估计方法。目标函数在一般线性回归的基础上加入了正则项（惩罚函数），可以压缩特征系数并使某些特征系数（权重）变为0，使用较少的非0系数进而达到特征选择的目的，使用较少的特征建模，使得模型训练尽可能的“简单”，使得模型的泛化能力较强［18-19］。

表1 ERA5再分析数据28个气象要素场Table 1 28 meteorological element fields from ERA5 reanalysis data

1.2.2随机森林

随机森林（Random forest）算法是利用bootstrap技术从原始样本中抽取随机化样本（样本bagging）来构建单棵决策树。对于每个树节点，首先从原始特征随机抽样出部分或全部特征，然后从这些特征构成特征子空间中选择分裂特征和分裂点。选择标准是分类问题中的最大不纯度的减小或回归问题中最大均方差（MSE）的减小。不断循环上述过程来逐个构造树节点，直到达到停止条件。对于回归问题，模型输出值是随机森林中所有决策树输出结果平均值［20-21］。

1.2.3深度神经网络

深度神经网络由3部分构成，分别为输入层、隐藏层和输出层，其中隐藏层的层数可以有很多。在模型训练时，多层的深度神经网络参数通过反向传播（Back propagation，BP）算法实现学习和更新，通常利用梯度下降法计算目标函数梯度以更新权重系数，从而使目标函数最小化，模型输出值尽可能与实际值接近，而模型需要调整的参数是通过模型在训练集训练和验证确定的［22-23］。

1.2.4检验方法

均方根误差（Rootmean square error，RMSE）评估初霜冻日期预测值与观测值的差距，是预报预测中常用评估指标，同时也是机器学习回归模型性能评估和优化过程广泛使用的函数。均方根误差越小，初霜期预测越准确，表示模型预测性能越好。公式为

式（1）中，n为样本数；ytrue，i为第i个样本真值（即数据集标记）；ypredict，i为第i个样本预测值。

在预报预测中也常用距平同号率定性评估预测效果，同号率越高，初霜冻日期预测趋势越准确，表示模型预测效果越好。具体定义是在测试集上评估模型预测趋势与真值趋势相同的样本数与所用样本数的比值。预测趋势为预测值相比于对应样本气候平均态偏离度，真值趋势为真值相比于对应样本气候平均态偏离度。公式为

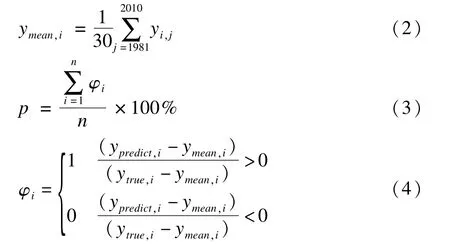
式（2）—式（4）中，n为样本数；yi，j为第i个样本第j个样本的真值（即数据集标记）；ytrue，i为第i个样本真值；ypredict，i为第i个样本预测值；ymean，i为第i个样本对应的1981—2010年气候平均值；φi为第i个样本预测值和真值趋势比值，相同趋势取1，相反趋势取0；p为距平同号率。

1.2.5模型构建

首先以不同起报时间划分数据集，以每年2—7月数据分别构建6个数据集，标记为对应年份的初霜冻日期。将数据集划分为训练集、验证集和测试集3部分。训练集和验证集用于交叉验证超参数调整确定性能最优模型，测试集用于评估模型预测性能（泛化能力）。从1961—2014年ERA5再分析数据中打乱随机抽取80%作为训练集，余下20%数据作为验证集；2015—2019年ERA5再分析数据作为测试集。基于机器学习算法的辽宁省初霜冻日期预测建模流程如图1所示，具体建模步骤如下：①数据预处理，初霜冻日期存在一定数量的缺测值，主要表现在某些站点在某些年存在缺测值，为了保持数据的完整性和准确性，直接剔除存在缺测的站点形成具有连续时间序列的初霜冻日期数据（共45站）。同时，对所有气象要素数据构成的特征矩阵进行标准化处理，可以避免特征间不同单位（尺度）的影响，还可以提高模型训练效率，加快收敛速度。根据不同起报时间（2—7月）将1961—2019年数据划分为6个数据集，每个数据集共有59个月，由逐年月再分析数据和同年的初霜冻日期组成，利用双线性空间插值方法形成相应的站点数据，因此每个数据集由大小为45×59共2655个样本组成，其中每个样本有28个特征因子。②特征选择，利用Lasso和交叉验证方法针对每个训练—验证集提取对初霜冻日期预测有重要影响的气象要素特征数据集。③模型训练，采用lasso回归、随机森林和神经网络算法分别利用特征选择出的特征数据集进行训练构建预测模型。④预测结果评估，将测试集输入到以上训练好的预测模型中，输出结果即为初霜冻日期，利用均方根误差和距平同号率评估模型预测性能。⑤归因分析，探讨关键气象要素对初霜冻日期预测的可能影响。

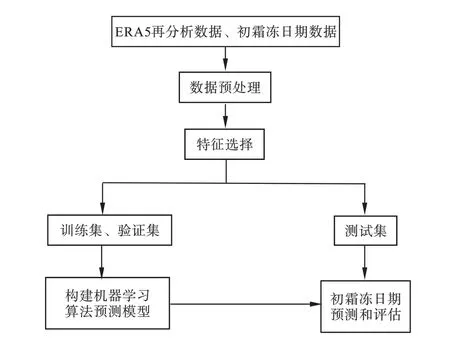
图1 初霜冻日期预测流程Fig.1 Flow chart of the prediction of the first-frost date

1.2.6特征选择

特征选择是利用机器学习算法从原始特征中选出对模型预测最有效的特征。特征选择主要有以下特点：①简化模型，增加模型的可解释性，去除冗余特征，降低学习难度，提高模型稳定性。②改善性能，大幅提高计算效率。③改善通用性、降低过拟合风险，减轻维数灾难，特征的增加可以更好地拟合训练数据，但可能在验证集和测试集上表现很差。常见的特征选择方法有过滤法（Filter）、包裹法（W rapper）和嵌入法（Embedded）。从模型性能来看，包裹法比过滤法更好，但包裹法计算负荷大，效率低［24］。因此，利用嵌入法中的Lasso模型进行特征选择，调用机器学习库基于该模型将特征选择和模型训练在同一个过程中完成，并且该方法计算效率高。

结合1.2.1节，由于Lasso模型加入正则化因子α‖w‖，以降低损失函数为目标，调节超参数α，加大惩罚力度，不重要的特征权重变为0，不仅可以降低过拟合风险，还可以提高计算效率。

2 结果分析

2.1 模型交叉检验及性能评估

如图2所示，采用Lasso回归、随机森林和神经网络算法进行2—7月辽宁省初霜冻日期预测。通过模型训练和超参数调节构建预测模型发现利用特征选择后特征训练的模型与利用全部特征训练的模型预测的RMSE基本一致，说明Lasso回归算法能够提取出对初霜冻日期预测有效的特征，利用这些特征建模完全可以替代全部特征。3种不同模型在各起报月预测性能差别不大，在验证集上RMSE为6—8 d，测试集上RMSE为8—10 d，其中Lasso回归和神经网络在4月和5月起报的预测效果最好，测试集RMSE在8—9 d。

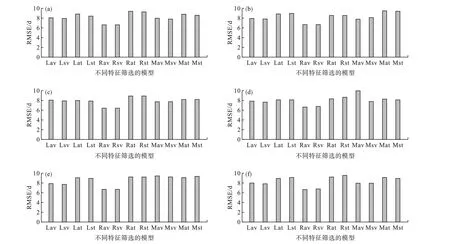
图2 2月（a）、3月（b）、4月（c）、5月（d）、6月（e）和7月（f）起报辽宁省初霜冻日期特征选择前后均方根误差Fig.2 Com parison of prediction performance of first-frost date before and after feature selection w ith p rediction starting from February（a），March（b），April（c），M ay（d），June（e），and July（f）

2.2 模型定量和定性预测性能评估

采用机器学习算法（Lasso回归、随机森林和神经网络）对辽宁省初霜冻日期进行预测，起报时间是当年2—7月并结合实际站点数据对模型预测性能进行客观评估。对各起报月（样本量5×45个）计算RMSE和距平同号率，结果如图3a所示。由图3a可知，RMSE随着预报时效的增加呈缓慢上升趋势，但整体差别不大（大都为8—10 d），其中4—5月起报RMSE最低（8—9 d），在3种模型中，Lasso回归预测性能最好。图3b表明，不同模型距平同号率随着起报时间增加呈波动变化，其中Lasso回归和神经网络模型在3月起报的距平同号率最低（约为53%），随机森林在7月起报最低（约为50%）；Lasso回归和神经网络模型在5月最高（约为68%），随机森林在3月起报最高（约为62%）。机器学习模型在不同起报时间下RMSE平均为9 d左右，平均同号率在60%以上，因此机器学习模型对初霜冻日期预测无论在定量还是定性预测上均有较好的表现（尤其4月和5月起报）。

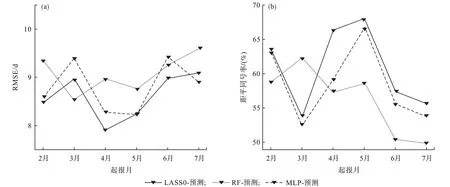
图3 2—7月起报的机器学习模型预测辽宁省初霜冻日期的均方根误差变化（a）和距平同号率（b）Fig.3 RM SE（a）and the rate w ith the same sign of anomaly（b）of the first-frost date in Liaoning province predicted by threemachine learning modelsw ith different prediction starting time

2.3 模型预测技巧空间分布及评估

分别采用Lasso回归、随机森林和神经网络方法对辽宁省初霜冻日期进行站点预测（起报时间仍为2—7月），定量定性评估模型预测性能。在测试集上，对不同起报月每个站点（样本量5个，2015—2019年）计算RMSE，结果如图4所示。由图4可知，随着起报时间的邻近，机器学习模型没有呈现出明显的线性趋势，RMSE变化不大（大都为6—11 d），其中Lasso回归和神经网络模型在4月起报的预测结果最好（RMSE为6—8 d），神经网络在5月起报的预测结果最好（RMSE在6—9 d），与图3a趋势基本一致，说明机器学习模型具有较高的预测精度。从RMSE分布来看，Lasso回归和神经网络预测的RMSE大都呈东高西低分布，随机森林大体呈东西高中间低分布。在定性预测上，对于不同起报时间大部分站点距平同号率超过50%，说明机器学习模型表现出较好的稳定性和准确率。

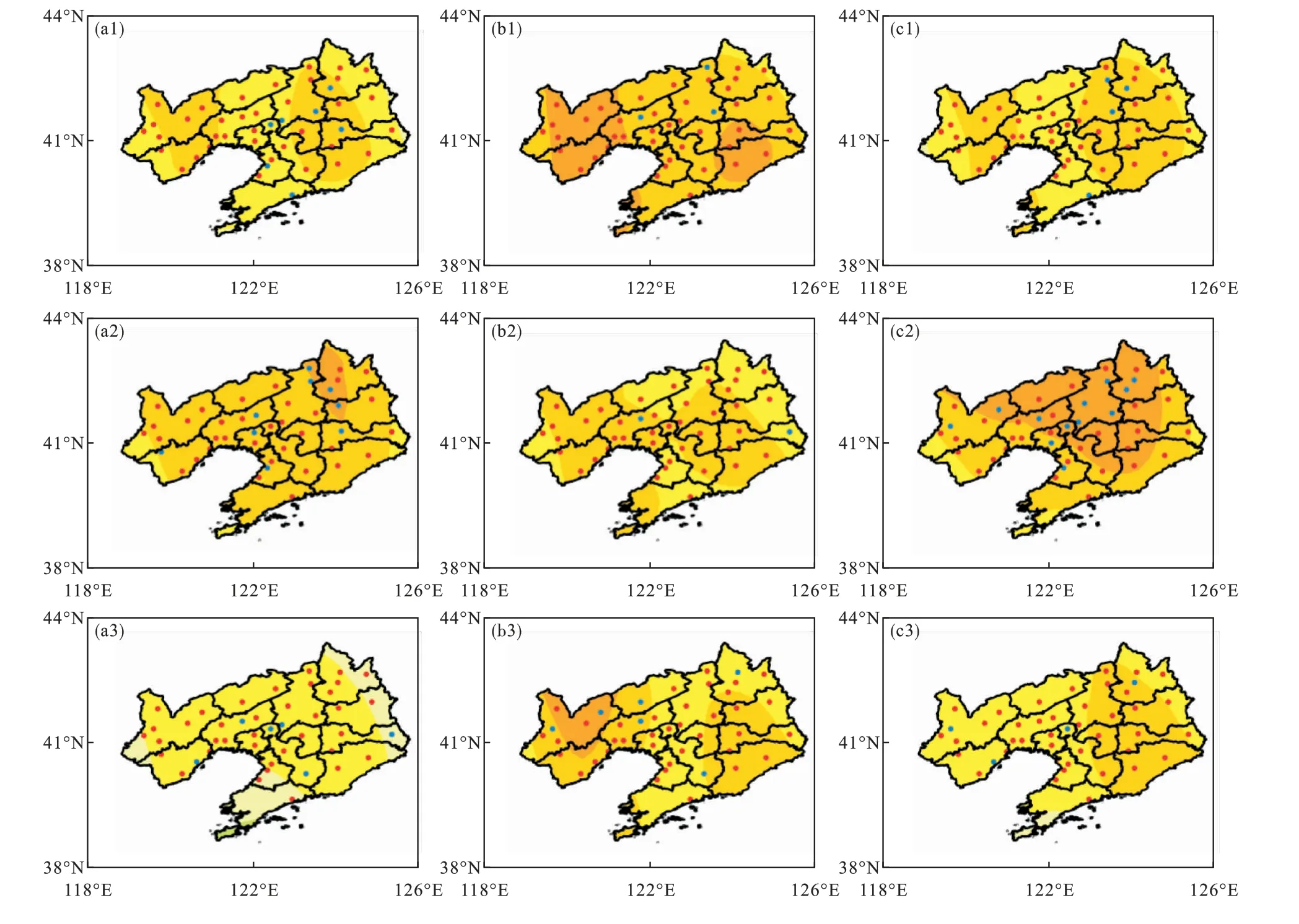
图4 2月（a1，b1，c1），3月（a2，b2，c2），4月（a3，b3，c3），5月（a4，b4，c4），6月（a5，b5，c5），7月（a6，b6，c6）起报Lasso回归（a）、随机森林（b）和神经网络（c）预测的辽宁省初霜冻日期均方根误差和距平同号率的空间分布Fig.4 Spatial distribution of RMSE and the rate w ith the same sign of anomaly of the first-frost date in Liaoning province predicted by the Lasso Regression（a），Random Forest（b），and Neural Network（c）modelsw ith prediction starting from February（a1，b1，c1），M arch（a2，b2，c2），April（a3，b3，c3），M ay（a4，b4，c4），June（a5，b5，c5），and July（a6，b6，c6）

2.4 特征选择及敏感性实验结果

利用Lasso回归算法的特征选择方法对所有起报月（2—7月逐月）进行特征提取，如表2所示数值代表各起报月的特征因子权重。特征因子对初霜冻日期预测输出值的影响程度与其权重绝对值的大小成正比，即特征因子绝对值的权重越大，表明该特征因子对初霜冻日期预测输出值的影响也就越大，负的特征权重表明该特征对初霜冻日期预测有负贡献，即该特征增加将会使得初霜冻日期提前，反之亦然。对起报时间（2—7月）的平均权重绝对值由大到小依次为（特征排列前10个）：低植被覆盖比例、64.0 cm土壤含水量、64.0 cm土壤温度、高植被覆盖比例、500 hPa位势高度、500 hPa温度场、3.5 cm土壤含水量、低植被用地所有叶子一侧表面积、194.5 cm土壤含水量、土壤类型。在以上特征因子中：①低植被用地所有叶子一侧表面积的权重随着起报时间临近而减小。②高植被覆盖比例、64 cm土壤温度的权重是随着起报时间临近而增大。③低植被覆盖比例、64 cm土壤含水量、500 hPa位势高度、500 hPa温度、3.5 cm土壤含水量、194.5 cm土壤含水量、土壤类型的权重与起报时间没有明显的相关关系。

植被覆盖对局地气候具有重要的调节作用，植被覆盖率越高越有利于地表含水量保持，出现降温越容易产生霜，初霜冻日期也就越易提前。植被覆盖（高植被覆盖比例、低植被用地所有叶子一侧表面积、低植被覆盖比例）对初霜冻日期预测均为负贡献（表2）。土壤水的体积（3.5 cm土壤含水量、64.0 cm土壤含水量、194.5 cm土壤含水量）与土壤质地（或分类），土壤深度和底层地下水位有关，不同深度的土壤水体积对初霜冻日期预测的贡献也有较大不同，3.5 cm土壤含水量、194.5 cm土壤含水量对初霜冻日期预测大都为负贡献，有利于初霜冻日期提前，而64.0 cm土壤含水量对初霜冻日期预测为正贡献，有利于初霜冻日期延后。64.0 cm土壤温度是第3级（在第3层中间）的土壤温度，5—7月起报的该要素对初霜冻日期预测为正贡献。土壤类型是ECMWF综合预测系统（IFS）的地表方案使用的土壤质地（或分类），用于预测土壤水分和径流计算中的持水量，土壤质地越细密、有机物含量越大，越有利于初霜冻日期推迟。高空要素中500 hPa位势高度对初霜冻日期预测为负贡献，对流层中层位势高度越高，越利于初霜冻日期提前，而500 hPa温度场对初霜冻日期预测为正贡献，对流层中层温度越高，越利于初霜冻日期延后。在以上要素中，低植被覆盖比例最重要，以4月起报为例，对低植被覆盖比例因素的影响进行评估（图5），发现大部分地区RMSE在7—10 d，东部和西部地区RMSE大于中部地区，去掉低植被覆盖比例因素后，Lasso回归和神经网络预测结果的RMSE均有比较显著的上升，表明低植被覆盖比例对模型的预测性能确实有重要影响，也反映出利用Lasso算法对原始特征进行特征选择的合理性。同时也发现，去掉低植被覆盖比例因素对距平同号率影响不大。辽宁全省大部分站点初霜冻日期同号率达到50%以上，说明机器学习模型在初霜冻日期定性预测上也表现出较好预测效果。

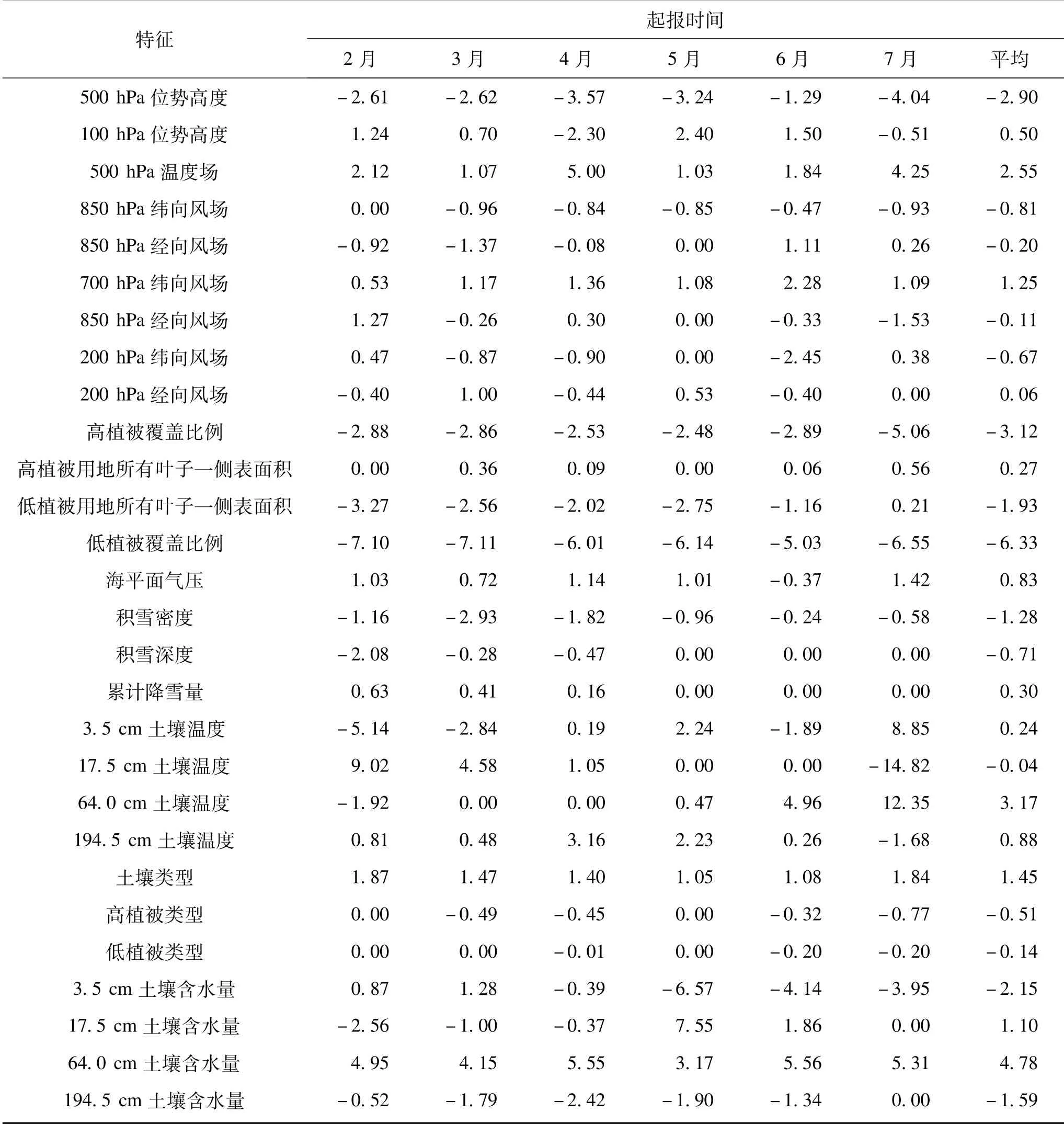
表2 2—7月起报的辽宁省初霜冻日期预测模型特征权重分布Table 2 Distribution of feature weights of the first-frost date in Liaoning province w ith prediction starting from February to Ju ly

图5 有（a）和无（d）低植被覆盖比例因素的Lasso回归、有（b）和无（e）低植被覆盖比例因素随机森林、有（c）和无（f）低植被覆盖比例因素的神经网络预测的辽宁省初霜冻日期均方根误差和距平同号率分布Fig.5 Distribution of RMSE and the rate w ith the same sign of anomaly of the first-frost date in Liaoning province predicted by Lasso Regression，Random Forest，and Neural Network models w ith（a-c）and w ithout（d-f）low vegetation coverage scale

3 结论与讨论

（1）对于不同起报时间，各机器学习模型预测的RMSE总体变化不大（大都为6—11 d），但不同模型有所差异，Lasso回归4月起报预测效果最好（RMSE为6—8 d），神经网络为5月起报的预测效果最好（RMSE在6—9 d）。对于不同模型，RMSE分布有所不同，Lasso回归和神经网络大都呈“东高西低”分布，随机森林大体呈“东西高中间低”分布，总的来说不同模型预测的初霜冻日期的RMSE分布比较均匀，因此机器学习模型具有优秀、稳定的预测效果。

（2）在定性预测上，大部分站点距平同号率为50%—70%，不同模型对于不同起报时间同号率表现也有不同，Lasso回归和神经网络模型距平同号率为3月起报最低（约为53%），5月起报最高（约为68%），随机森林为7月起报最低（约为50%），3月起报最高（约为62%）。因此，机器学习模型表现出较高准确率。

（3）Lasso回归算法不仅可以构建初霜冻日期预测模型，还在特征选择上表现非常优秀。特征选择结果表明，对初霜冻日期预测有影响的关键特征（按平均权重由大到小排序前10个）分别为低植被覆盖比例、64.0 cm土壤含水量、64.0 cm土壤温度、高植被覆盖比例、500 hPa位势高度、500 hPa温度场、3.5 cm土壤含水量、低植被用地所有叶子一侧表面积、194.5 cm土壤含水量、土壤类型。通过机器学习特征选择算法获得的气象要素特征集不仅可以提高模型预测效果，而且从一定程度上也有助于加深对以往建立初霜冻日期的预测物理统计模型所使用的气象要素组合的认识。

（4）从特征重要性的分析结果看，3—5月起报的64.0 cm土壤温度权重最接近于0（权重分别为0.00、0.00、0.47），排除这个特征建模可能有利于3—5月起报模型预报效果的改善，但具体物理机制还需要进一步分析。低植被覆盖比例因子对辽宁省初霜冻日期预测影响较大，去掉这个特征建模输出的初霜冻日期预测效果显著下降，尤其是Lasso回归和神经网络模型。

（5）机器学习算法对辽宁省初霜冻日期预测具有良好的效果。初霜冻日期预测较大程度上依赖于前期预测因子选择，不同特征因子集合对预测性能影响较大，在下一步工作中需要尝试不同特征选择方法提取对预测效果最优的特征组合。另外，虽然机器学习模型具有一定的可解释性，但该模型不能有效揭示特征要素之间内在相互作用的动力学机制，在下一步工作中需要结合经典气候动力学理论和方法分析其可能原因。另外通过前期单月数据建模可能难以考虑连续多月数据之间相互作用，利用多月数据建模的预测效果如何，有待于在以后的工作中进行深入研究。