一个含参数半离散型的Hilbert型不等式

有名辉

(浙江机电职业技术学院 数学教研室，浙江 杭州 310053)

0 引 言

20世纪初，德国数学家Hilbert在一次积分方程的讲座中提出一个有关二重级数的不等式[1]:

(1)

(2)

同时，Hardy等[1]还建立了式(2)积分形式的类比: 若f(x)、g(x)>0，且f∈Lp(R+)、g∈Lq(R+)，则

(3)

式(1)被称为 Hilbert不等式，π是最佳常数因子.式(2)和式(3)被称为Hilbert型不等式，π/sin(π/p)是最佳值.

20世纪90年代后，通过构造新的核函数，引入参数，借助近代分析的技巧， 研究者们建立了大量与式(2)和式(3)类似的Hilbert型不等式，其中积分型结果见文献[2]～[9]，离散型结果见文献[8]～[13].值得指出的是，Hilbert型不等式通常可分为齐次型和非齐次型.对非齐次离散型的Hilbert型不等式，其常数因子的最佳性很难通过构造方法来证明.因此，研究者们往往会研究其对应的半离散形态，相关成果见文献[14]～[16].本文将构建一个包含齐次和非齐次两种形态的半离散型核函数，并借助权系数方法和分析技巧，建立一个最佳常数因子半离散型的Hilbert型不等式.为行文方便，本文约定p>1,1/p+1/q=1.

1 引 理

证明对K(z)求导，可得：

故K(z)在R+上单调递增，且K(z)>K(0)=0.

证毕.

引理2设λ>β>0，γ>0>τ>-γ，K(z)如引理1定义，则

(4)

证明由于γ>0>τ>-γ，故

且

分部积分，可得：

(5)

在式(5)中，令βzγ=u，并利用以下等式[17]：

可得：

(6)

类似地，令λzγ=u，则

(7)

将式(6)和式(7)代入式(5)，可得式(4).

证毕.

其中,E={x:x>0,xsgna>1}，则

(8)

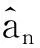
(9)

当a<0时，根据Fubini定理[18]，可得:

(10)

结合式(9)和式(10)，可得式(8).当a>0时，类似可证式(8)成立.

证毕.

2 主要结果

(11)

(12)

其中,

因bτ<1，故nbτ-1关于n单调递减.由b<0及引理1，可得K(xanb)关于n也单调递减.因此，令xaub=z，借助引理2，可得:

(13)

类似可得:

(14)

将式(13)和式(14)代入式(12)，可得式(11).

下面证明式(11)的常数因子不可改进.

假设存在正常数A， 满足

(15)

且

(16)

(17)

结合式(8)和式(17)，可得：

令s→+∞，并利用式(4)，得：

显然，这与式(15)矛盾.故式(11)的常数因子是最佳值.

证毕.

在定理1中， 令a=-b=1， 则有以下推论：

3 结 语

本文通过引入多个参数，构造了一个新的含有对数函数的核函数，并建立了相关的半离散Hilbert型不等式.虽然核函数的构造过程是初等的,但也具有一定的创新性，即所建立的结果同时包含了齐次和非齐次两种情形,且证明过程采用的方法对相关研究工作具有一定的借鉴意义.