基于CFD的安全壳内浮力驱动自然对流特性分析
2022-09-21邓豪放王安庆吕续舰
邓豪放王安庆吕续舰
1(南京理工大学能源与动力工程学院 南京 210094)
2(中国电力科学研究院有限公司 北京 100192)
研究封闭空腔内自然对流换热现象,对于核反应堆安全壳安全十分重要[1]。相关研究结果对安全壳内气体流动换热计算模型的开发和推广具有重要意义。封闭空腔内的自然对流及换热现象是传热学、流体力学等学科研究的重要课题之一,在核科学等工程领域有着广泛的应用,因此国内外诸多学者都对此开展了实验和数值模拟研究。Barakos等[2]使用控制体积法研究了差异加热空腔内基准问题;Ampofo等[3]测量了0.75 m×0.75 m×1.5 m空腔内自然对流实验的基准数据;尧俊等[4]利用矩形封闭空腔开展了底部弧形面自然对流换热实验;王炜波等[5]进行了单侧加热矩形通道内混合对流换热的实验研究。除实验之外,研究人员还使用计算流体力学(Computational Fluid Dynamics,CFD)软件对此进行了数值模拟研究[6‒9]。
在封闭空腔对流换热基准问题研究基础上,各研究机构通过建立安全壳模型来研究安全壳内的传热现象及气体分布等问题。其中德国Becker科技公司 建 立 的THAI(Thermal-hydraulics,Hydrogen,Aerosols and Iodine)系列实验装置有较好的代表性。TH21实验是此系列实验中的一个基础性实验,该实验研究了对容器壁进行不同温度加热和冷却作用而产生的自然对流现象,为后续实验研究奠定了基础[10‒11]。由于THAI实验为相关计算程序的开发和验证提供了大量实验数据,国内外诸多学者都对此进行了大量研究。胡效明等[12]使用CFX程序对THAI HM-2实验进行了验证,分析了安全壳壁面的换热和蒸汽冷凝情况下氦气(氢气代替工质)的流动扩散分布;Kelm等[13]使用OpenFOAM定制求解器“containmentFOAM”对安全壳中H2与空气混合分布过程进行研究,得到了比通用CFD软件更优的模拟结果;Zhang等[14]利用GASFLOW-MPI中三种湍流模型对安全壳内气体分层展开模拟研究,并与TH20实验进行对比,得出大涡模拟能准确反映实验现象;Hu等[15]利用GASFLOW-MPI程序对TH22实验进行模拟和分析,清楚地捕获了安全壳内氦气的浓度和温度分布;Dehbi等[16]利用非定常RANS模型对TH24自然循环实验进行计算,证明了气体辐射对自然对流及气体混合过程的影响作用。
由于核反应堆事故时安全壳内气体行为具有较高的复杂性,气体组分众多,并伴随着辐射和换热现象,需要对其机理进一步研究。为此,本文针对核反应堆安全壳内浮力驱动的自然对流换热现象,采用CFD方法进行数值研究。首先确认了CFD方法对模拟封闭空腔内自然对流和换热现象的适用性和准确性,随后针对THAI-TH21模型开展计算分析,并与实验数据进行了比较分析,研究了安全壳内辐射换热及浮力驱动的自然对流现象。研究结果作为安全壳内气体复杂流动换热的基础,可进一步分析多组分气体的实际流动换热现象。
1 计算模型
1.1 计算方法
本文基于有限体积方法,将流体域划分成为若干个控制体单元,在每个控制体单元内使用离散化方法求解瞬时Navier-Stokes方程(N-S方程),即质量、能量和动量守恒方程,求解得到各点参数在空间内的分布。三个守恒方程分别如下所示[17‒18]。
质量守恒方程:
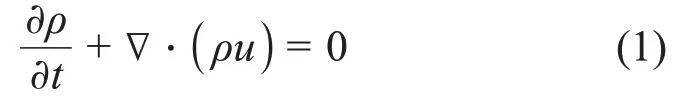
动量守恒方程:
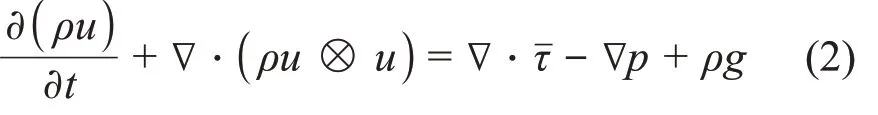
能量守恒方程:

式中:ρ为流体密度,kg∙m‒3;t为时间,s;u为流速,m∙s-1;τˉ为粘性应力张量,N∙m‒2;p为压力,Pa;g为重力加速度,m∙s-2;h为流体的比焓,J∙kg-1;K为流体动能;α为导热系数,W∙(m⋅K)-1;Srad为辐射源项,W∙m-3。
焓与温度的关系为:

式中:cp为比定压热容,J∙(kg·K)-1;T为流体温度,K。
在本研究中,差异加热空腔和THAI-TH21模型均采用剪切应力SSTk-ω湍流模型,并激活Full Buoyancy Effects(浮力效应)。压力插值项为Body Force Weighted,干空气介质密度模型为Boussinesq,均采用Couple求解器开展计算。
1.2 辐射模型验证
首先对Discrete Ordinates(DO)辐射模型计算封闭空腔内的辐射换热现象准确性进行评估。所用模型为简单立方体模型(图1),其中6个面的表面发射率和温度值如表1所示。将立方体的面净辐射热流量(Φr)作为验证参数,如果壁面是辐射的净接收者,则Φr为正值;如果壁面是辐射的净发射者,则Φr为负值。通过将多表面系统辐射传热的角系数法[17]计算得到解析解和用DO辐射模型得到的数值解进行比较,验证辐射模型的适用性。两种方法得到的结果如表1所示,从中可以得出,用DO辐射模型计算得到的Φr值与解析解相比,相对误差最大为3.79%。因此,DO辐射模型可以较好地模拟封闭空腔内的辐射换热现象。

图1 辐射热流计算的简单立方体模型Fig.1 Simple cube model for calculating radiant heat flow
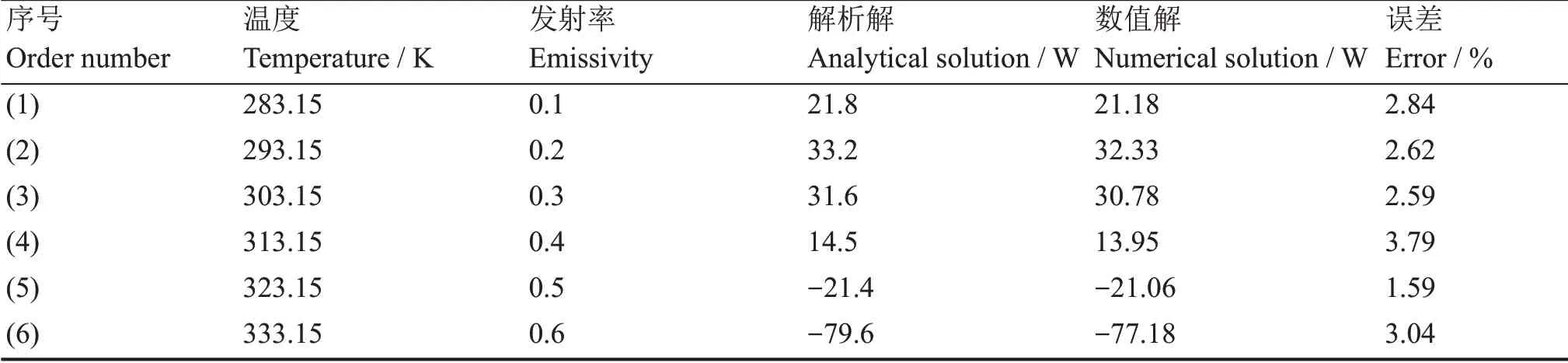
表1 辐射模型验证Table 1 Radiation model validation
为进一步探究封闭空间内辐射效应对换热的影响,选择差异加热空腔内自然对流的实验基准数据[3]作为模拟结果的验证。差异加热空腔(图2)的热壁面和冷壁面分别保持在323.15 K和283.15 K,顶部和底部的壁面与周围环境绝热。此模型用于分析二维情况下空腔内的自然流动及辐射换热现象,研究结果将应用于后续THAI-TH21模型的模拟中。用于差异加热空腔和TH21模型的干空气热物理性质如表2所示,钢结构壁面和绝热壁面的材料物性如表3所示。

表3 钢和绝热壁面材料特性Table 3 Material properties of steel and insulation wall
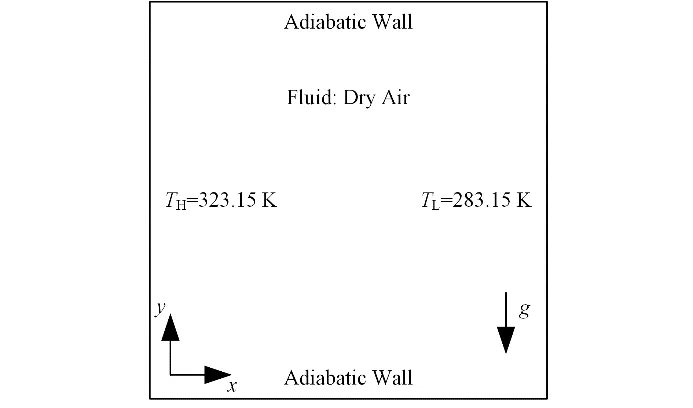
图2 差异加热空腔示意图Fig.2 Schematic diagram of differentially heated cavity

表2 干空气热物理性质Table 2 Material properties of dry air
1.2.1 近壁面分析处理
对于自然对流,通常有以下两种方法来模拟近壁面区域:一是不使用壁面函数,对壁面附近网格进行加密处理,完全解析近壁面边界层;二是将第一个网格节点设置在粘性底层之外(y+>6),使用壁面函数对近壁面进行求解。相比而言,第一种方法更为精确,但会大大增加网格数量,使计算成本增加;第二种方法降低了对近壁面处网格的要求,提高了计算效率,因此应用较为广泛。
本文分别采用这两种不同方法,对y+足够小的网格(y+<2),完全解析边界层;对第一个网格节点位于粘性底层之外的网格(y+>2),采用标准壁面函数对近壁面进行求解。
定义局部努塞尔数[3]如下:
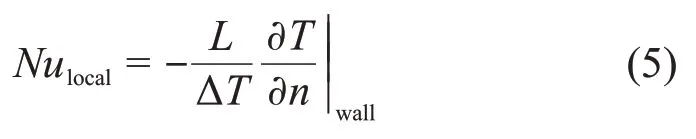
式中:L为特征长度;T为温度,K;ΔT为冷热壁面温差。
根据不同模拟方法得出的局部努塞尔数和实验数据对比如图3所示。从图3中可知,采用标准壁面函数进行计算时,局部努塞尔数误差较大。因此,对于自然对流问题,若要精准捕捉近壁面流动及温度分布情况,必须保证y+<2来对近壁面边界层进行求解。
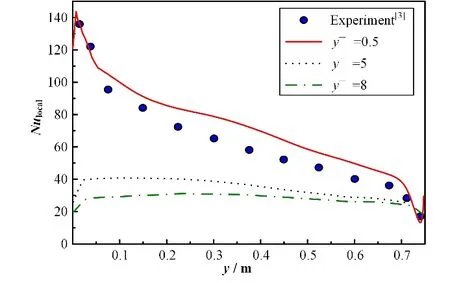
图3 不同y+下局部努塞尔数对比图Fig.3 Comparison of local Nusselt number under different y+
1.2.2 计算模型验证
为验证计算模型的可靠性,分别计算了差异加热空腔一半高度处(y=0.375 m)的速度和温度分布,并与实验数据进行比较,如图4所示。可以发现,速度分布和温度分布相对于空腔中心近似是中心对称的,在水平方向上,两个等温壁面附近的温度分布和速度分布存在着一个急剧变化。从x=0.075~0.675 m范围内,空腔内在远离壁面区域流体几乎处于静止状态。在远离壁面的差异加热空腔中部,计算结果与实验数据吻合良好,在近壁面附近,实验数据与数值模拟结果变化趋势一致,数值上有一定的误差,但误差均在10%以下。总体而言,此计算方法对空腔内的温度及速度分布可以作出较为准确的模拟,即可将此模型及计算方法用于后续安全壳的计算研究。
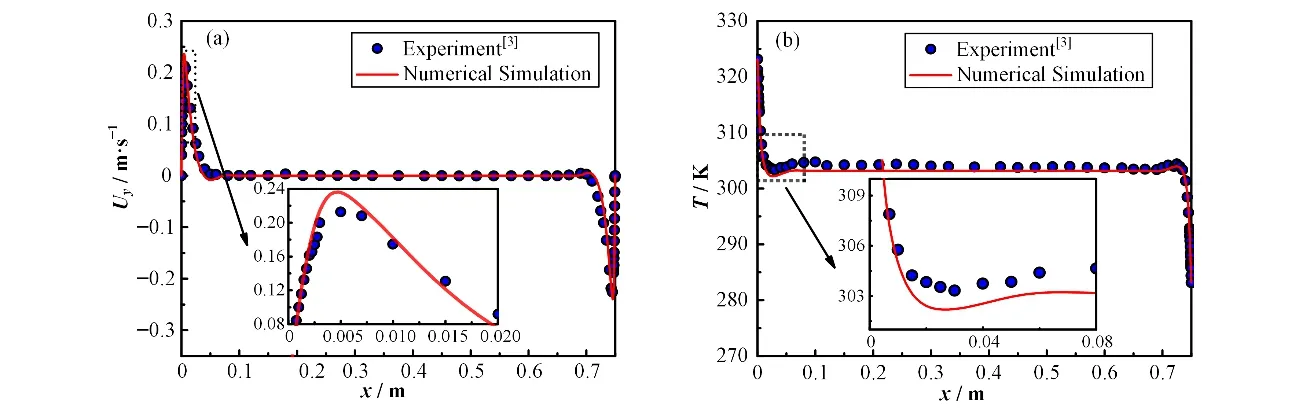
图4 差异加热空腔中部速度(a)和温度(b)分布Fig.4 Velocity(a)and temperature(b)distribution in the middle of differentially heated cavity
1.2.3辐射作用影响分析
由于差异加热空腔模型为绝热封闭空腔,热壁面上的壁面平均热流密度值均有冷壁面上与其数值相等,符号相反的热流密度值相对应(图5),此外腔体表面辐射换热效应会抑制自然对流,对流效应的减弱主要由辐射效应进行补偿,这与Sharma等[19]的研究结果是一致的。

图5 差异加热空腔冷热壁面平均热流密度Fig.5 The average wall heat flux of differential heating cavity
为进一步了解辐射作用的影响,将有无辐射作用下空腔中部温度值与实验值进行对比,对比图如图6所示,可以得出,模拟计算得到的空腔中部温度分布结果在远离壁面处与实验数据吻合良好,在靠近壁面处存在一定的误差。经分析,引起误差的原因为边界条件设置问题,此算例在模拟中,冷热壁面的发射率被设置为恒定值(ε=0.3),但实验中并未对壁面发射率作具体说明,除此之外,实验中顶部和底部也不是模拟计算时设置的那样完全绝热,因此近壁面处会存在较大误差。从有无辐射情况下封闭空腔内的温度分布云图(图7)可以看出,在这两种情形下,封闭空腔内部的温度都呈层状分布,与无辐射的情况相比,在考虑辐射作用的情况下,腔体在垂直方向上的温差更小,空腔内的温度分布更加均匀。
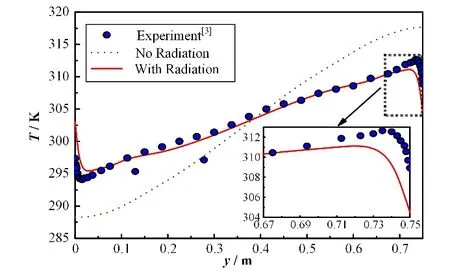
图6 差异加热空腔中部温度分布Fig.6 The temperature distribution in the middle of differentially heated cavity

图7 差异加热空腔温度云图Fig.7 The temperature contour of differentially heated cavity
2 计算结果分析
2.1 核反应堆安全壳模型
本文采用的核反应堆安全壳模型是THAI实验模型[11],该模型具有工业规模的多隔间,常用于研究在严重事故期间核反应堆安全壳中的气体流动、温度分布及传热现象。THAI实验模型的主体部分是一个60 m3的不锈钢容器,高9.2 m,直径3.2 m,如图8所示。装置外部壳体装有恒温夹套,用于保持壁面的恒温条件,装置的内部部件可以更换,可用于研究不同条件下的实验现象。
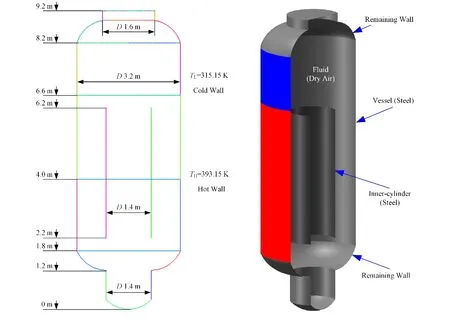
图8 THAI实验装置几何参数和CFD模型Fig.8 Geometric parameters and CFD model of THAI facility
对于TH21模型,为简化计算,忽略了内筒的支撑结构。在此模型中,设定加热和冷却壁面为等温边界条件,其余外壁面为混合边界条件。THAI网格由六面体结构网格组成,在靠近容器壁面、内筒壁面和冷热壁面的交界处均做加密处理(图9),网格加密方法与差异加热空腔模型壁面附近网格加密方法一致,以便更好捕捉壁面处的流动和温度分布。

图9 TH21核反应堆模型网格Fig.9 Diagram of TH21 reactor model grid
在进行TH21模型网格无关性研究时,如与实际模型设置保持完全一致,计算成本和时间将大幅提高。因此对计算模型进行合理简化,简化后的计算模型仅设置三个不同的壁面条件:壁面1(安全壳内表面)、壁面2(内筒内表面)和壁面3(内筒外表面)。其中壁面1和壁面2温度T=393 K,发射率ε=0.5,壁面3温度T=367 K,发射率ε=0.1。以壁面3壁面辐射热流量Φ为参数,来研究TH21模型的网格无关性。分别计算了148W、212W和302W三种网格数量下的壁面3平均热流密度值Φ,结果如图10所示。其中212W网格相对于148W网格的误差为1.259%,302W网格相对于212W网格的误差为0.101%,可认为212W网格数量达到收敛状态。在本研究中,TH21模型均采用212W网格数量进行后续计算。

图10 TH21模型网格无关性验证Fig.10 Verification of grid-independence of TH21 model
2.2 安全壳内温度和压力分布特性
在TH21实验中[20],安全壳内空气在40 500 s内从初始大气压力(101 325 Pa)升高至124 000 Pa。整个实验过程分为两个阶段:压力和温度上升的升温升压阶段和压力达到稳定的准静态阶段。在升温升压阶段初期,数值模拟得到的压力值与实验值几乎相同;在升温升压阶段后期,数值模拟得到的压力值逐渐高于实验值,到达准静态阶段后,计算压力值与实验值差值趋于稳定。具体原因为,在升温升压阶段初期,气体温度较低,壁面散热产生的影响较小,随着气体温度升高,实际实验中散热量增加,使得计算得到的压力值逐渐高于实验值。数值模拟得到的准静态阶段压力值为126 000 Pa,与实验值相比,最大误差为1.61%。整个过程压力变化曲线与实验值对比如图11所示。由于实验时实验装置壁面存在热量损失,热量损失具体数值未知,因此无法在计算时对散热量作出精确设置,所以在模拟时未设置热量损失,这也是模拟得到的稳态压力值高于实验值的原因。从准静态阶段压力云图(图11)可以看出,整个容器内压力呈层状分布,上高下低,气体对安全壳上部壁面产生的压力载荷较大。
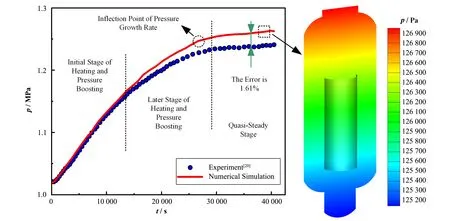
图11 压力随时间变化曲线及准静态阶段压力云图Fig.11 The pressure-time curves and the pressure contour of quasi-static stage
在TH21实验中,装置内气体的流动是由浮力驱动的,y方向上的气体密度不同是产生浮力的原因,密度不同是由壁面温度不同引起的,因此应关注TH21装置内不同半径处温度值随高度的变化。根据实验时装置内热电偶的分布选取了两条距中心线不同距离的竖直线来监测温度值分布,分别是内筒外侧和外壁面内侧的中间位置(r=1.15)和接近外壁面内侧的近壁面处(r=1.50),计算得到的这两条直线上温度值随高度变化与实验值对比曲线如图12所示。从图12可以得出,在靠近冷壁面的位置(y>6.6 m),CFD模拟计算结果与实验数据吻合较好。在冷热壁面交界高度处,由于冷热壁面温差引起工质的流动掺混,此高度处温度值产生“突变”。在靠近热壁面的位置(y=1.8~6.6 m),计算结果与实验结果温度值分布趋势类似,但在温度数值上存在误差,相对误差均在2%以下。误差的原因为实验时热电偶未对辐射效应进行标定,使得热电偶在测量有辐射作用时的温度值出现了误差。辐射效应对热电偶的影响主要表现在热壁面附近,所以在热壁面附近模拟得到的温度值与实验值存在误差。值得注意的是,在热壁面附近的环形空间内,不同半径处的温度值出现了“交叉”,结合图13速度流线图可知原因为环形空间内存在较弱的对流回路,使得回路附近不同半径处的温度值产生“交叉”。在模拟达到准静态阶段后,处理得到z平面温度云图如图12所示。从准静态阶段温度云图中可以得出,准静态阶段时TH21安全壳内温度接近于均匀状态,高温区分布在热壁面和内筒外壁面附近,低温区分布在冷壁面和安全壳最底部。

图12 不同半径处温度随高度变化曲线及准静态阶段温度云图Fig.12 Curve of temperature variation with height at different radius and temperature contour of quasi-static stage
图13为不同高度处速度随半径变化曲线以及z平面速度流线图。从速度随变化曲线可知,在不同高度处,热壁面附近流体流速均是同一高度处最高的。在h=3.5 m和4.9 m时,由于内筒壁面的辐射作用,内筒外表面的温度要高于流体温度,因此内筒外壁面附近和热壁面附近流体流速均高于环形空间内流体流速。随着h的增加,热壁面对流体的加热作用逐渐累积,空气温度也随之增高,流速也逐渐升高,因此4.9 m高度处流速高于3.5 m处流速。h=6.4 m时,由于冷热流体的交汇在交界处产生回路,因此在半径0.6~1.3 m之间,y方向流速无明显变化。从流线图可以看出,由于壁面的温差作用,在热壁面附近产生上升流动,在冷壁面附近产生下降流动。热壁面附近的上升流动和冷壁面的附近的下降流动在交界处形成回路。流场存在两个主要的对流回路,由上升流动和下降流动交汇产生。在热壁面和内筒之间的环形空间内,存在一些较弱的对流回路。在TH21模型的顶部和底部空间中,只存在较弱的流动现象,气体流动可忽略不计。
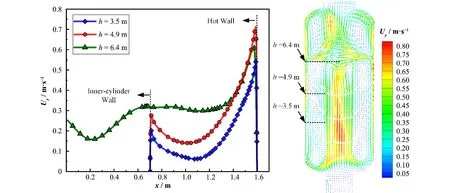
图13 不同高度处速度随半径变化曲线及准静态阶段流线图Fig.13 Curve of velocity variation with radius at different heights and stream pattern of quasi-static stage
3 结语
本文基于CFD方法对封闭空间内的自然对流换热现象以及TH21实验进行了计算分析,并与实验结果进行了对比,得到了以下主要结论:
1)对DO辐射模型的验证和对差异加热空腔模型分析证明了DO辐射模型对计算封闭空间内自然对流及换热现象的适用性。对差异加热空腔的分析中得出在模拟自然对流现象时要保证近壁面y+<2,完全解析近壁面边界层,并且在计算研究时应开启辐射模型,考虑辐射效应对流动换热的影响。
2)在TH21实验中,由于壁面热量损失数值未知而无法精确模拟,导致得到的稳态压力值高于实验值约为1.61%。对准静态阶段TH21装置内温度分析得出,在冷壁面附近区域,工质气体(干空气)的温度分布与实验数据吻合良好,在热壁面附近计算结果与实验数据存在误差,最大误差小于2%。
3)辐射效应会使内筒外壁面温度升高,使得内筒附近气体流速增加。在热壁面和内筒之间的环形空间内,存在一些较弱的对流回路,环形空间内对流回路为同一高度不同半径处温度值产生“交叉”的原因。
作者贡献声明邓豪放:仿真计算,初稿撰写;王安庆:仿真模型调试;吕续舰:课题指导,稿件修改。
