基于自适应RBF神经网络预测堆芯热工水力参数的方法研究

冀 南易金豪赵鹏程,2于 涛,2

1（南华大学核科学技术学院 衡阳 421001）

2（南华大学核燃料循环技术与装备湖南省协同创新中心 衡阳 421001）

反应堆关键热工参数（如燃料包壳表面最高温度）与核电厂的经济性和安全性密切相关。在较短时间内准确预测反应堆在各种工况下的关键热工参数及其变化趋势，有利于提高反应堆设计效率和保障运行中的安全，能够使操作员和核电厂系统在事故情况下提前作出响应，大幅度提高反应堆的安全性，有效防止核电厂事故的发生。然而，在反应堆运行过程中，关键热工参数同时受到多个物理量的影响，其变化较为复杂，传统预测方法难以在短时间内实现准确预测。因此，为提高反应堆运行的安全性，有必要发展新的反应堆关键热工参数预测方法。

神经网络（Neural Network，NN）是一种模拟动物神经元行为特征进行信息处理的数学模型。由于其具有非线性、大规模、并行处理能力强、鲁棒性、容错性及自学习能力强等特点，已经被成功在多个领域进行应用，如非线性函数逼近、数据分类、模式识别、信息处理、图像处理、控制和故障诊断、金融预测、时间序列预测等［1］。

从20世纪90年代开始，国内外许多学者开始使用各种神经网络算法进行堆芯参数的预测。黄彦平等［2］采用反向传播（Backpropagation，BP）人工神经网络对反应堆临界热流密度进行预测，与传统方法相比，该方法预测精度高，更新与使用更为方便，更易于推广；李辉等［3］基于10 MW高温气冷堆，通过人工神经网络的方法监控和分析反应堆在各种故障下，各参数的变化情况，以此来判断反应堆的故障情况；Mohamedi等［4］通过人工神经网络方法开发了一种新的自定义函数用于计算流体动力学（Computational Fluid Dynamics，CFD）模拟核反应堆燃料组件的水蒸气多相流动，结果表明：人工神经网络预测的最大绝对误差约为3%，预测精度符合要求；彭星杰等［5］提出可使用正则化径向基（Radial Basis Function，RBF）神经网络模型重构堆芯轴向功率分布，并对ACP-100模块化反应堆的功率分布开展研究，研究发现，该方法可以精确地重构出堆芯轴向功率分布，并且具有良好的鲁棒性，可以克服功率分布重构中存在的固有不适定性。现有关于堆芯参数预测的研究大多是在改进目前已被广泛使用的BP神经网络［6-7］，很少研究其他神经网络的应用。此外，目前研究大多集中于反应堆稳态参数预测和分析，瞬态工况下的研究较少，而瞬态工况是直接关系到反应堆运行安全，其变化趋势的预测更为重要。本文基于自适应的RBF神经网络对反应堆的稳态与瞬态的包壳最高温度进行预测，并与目前被广泛应用的自适应BP神经网络作对比，研究自适应RBF神经网络在堆芯关键参数预测的适应性。

本文首先采用快堆子通道分析程序Subchanflow计算产生数据样本，然后分别采用自适应RBF神经网络与自适应BP神经网络针对稳态单组件、以及瞬态反应堆堆芯数据进行训练，以燃料包壳表面最高温度为关键热工参数，比较分析了两种自适应神经网络预测模型在稳态和瞬态工况下的优劣，从而验证自适应RBF神经网络在堆芯关键参数预测上的适应性。

1 神经网络模型构建

1.1 自适应BP神经网络

BP神经网络是一种基于误差反向传播算法的前馈神经网络，它模仿人脑神经元对外部激励信号的反应过程，建立多层感知器模型，采用正向传播和误差反向传播算法（Error Backpropagation Algorithm），通过多次迭代学习能够存储大量的输入输出模式映射关系，而无需具体揭示这种映射关系的数学方程、能够成功地搭建出处理非线性信息的智能化网络模型，是目前应用最广泛的神经网络之一，其建模过程主要包括信息正向传递和误差反向传播［8］。

BP神经网络是一种具有三层或三层以上的神经网络，包括输入层（Input Layer）、隐藏层（Hidden Layer）和输出层（Output Layer），上下层之间全连接，而同一层神经元之间无连接。三层BP神经网络模型如图1所示，其输入维度为l，隐含层节点数为p，输出维度为q。

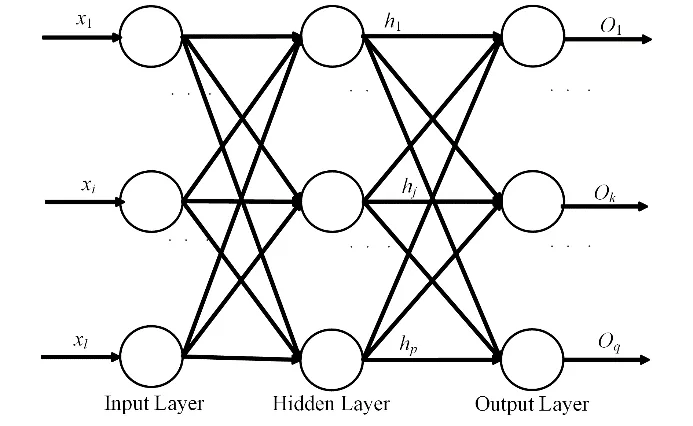
图1 三层BP神经网络结构图Fig.1 Structure diagram of 3-layer BP neural network

BP神经网络隐含层的输入、输出为：

输出层的输入、输出为：

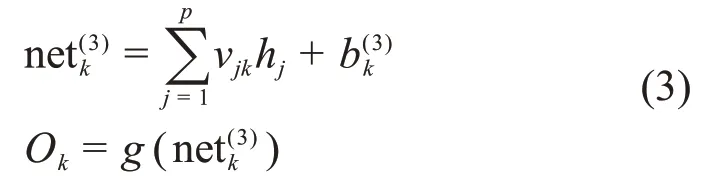
损失函数为：

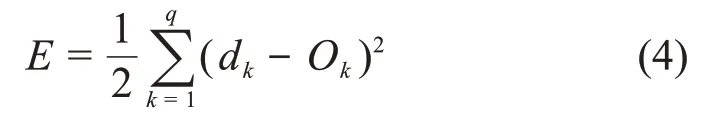
式中：wij为输入层到隐含层的连接权值；xi为输入层第i个节点的输入；b(2)j为隐含层第j个节点的偏置；net(2)j为隐含层第j个节点的输入；hj为隐含层第j个节点的输出；f(x)为隐含层的激活函数；vjk为隐含层到输出层的连接权值；b(3)k为输出层第k个节点的偏置；net(3)k为输出层第k个节点的输入；Ok为输出层第k个节点的输出；dk为隐含层的期望输出；为输出层的激活函数；E为损失函数。

BP神经网络结构相对简单，梯度下降较为稳定，理论上可以实现较高精度的非线性拟合，对于非线性函数逼近、时间序列预测等问题有一定的应用价值。但是BP神经网络由于学习率一旦确定便不再改变，使得学习过程很容易陷入局部极小值点，并且收敛速度慢，因此引入Adam自适应算法对梯度下降法［9］改进，让学习率能够自适应地根据损失函数的改变而变化，提高收敛速度。

Adam算法的参数更新方式如下：

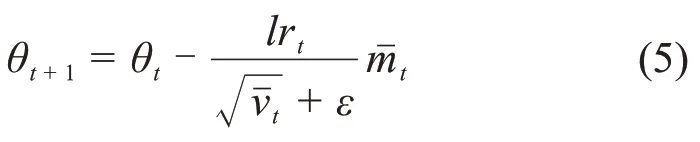
式中：θ为任意参数；lrt为学习率；ε为了保证除数不为0而设置为10-8；t为迭代次数；mˉt为过去梯度的指数衰减平均值，vˉt为过去梯度平方的指数衰减平均值。

1.2 自适应RBF神经网络模型

RBF神经元网络的产生具有很强的生物学背景，在人的大脑皮层区域中，局部调节及交叠的感受野是人脑反应的特点，基于感受野这一特性，Moody和Darken提出了一种神经网络结构，即RBF网络。

RBF神经网络是一种局部逼近的前馈神经网络，能够逼近任意的非线性函数，在处理系统内难以解析的规律性时，具有良好的泛化能力。由于RBF神经网络中间隐含层只有一层，所以与BP神经网络相比有很快的学习、收敛速度，并且隐含层用输入向量与中心向量间的欧氏距离作为自变量，用Gaussian函数作为激活函数，当输入距离激活函数中心越远时隐含层输出数值就越小，因此只有当输入与中心的欧氏距离越小时才会有真正的映射作用，所以它具有局部逼近的性质。Poggio和Girosi已经证明了广义RBF神经网络有着优越的连续函数逼进性能［10］，且抗噪能力强。目前，高斯径向基神经网络是最为常见的一种RBF神经网络，其网络结构和学习算法与BP神经网络有着很大的差别，在一定程度上克服了BP网络的容易陷入局部最优解以及收敛速度慢的缺点［11］。

图2为单个输出的RBF神经网络拓扑结构：图3给出了本文神经网络预测模型计算流程示意图。

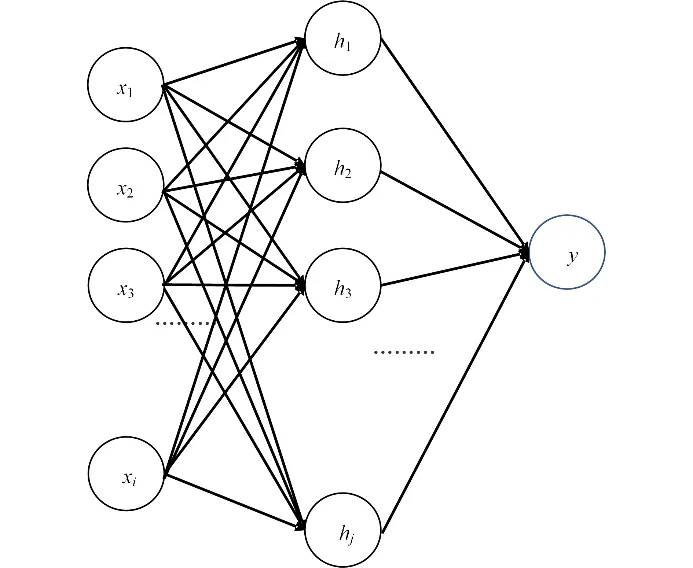
图2 单输出的RBF神经网络结构图Fig.2 Structure topological of single output RBF neural network

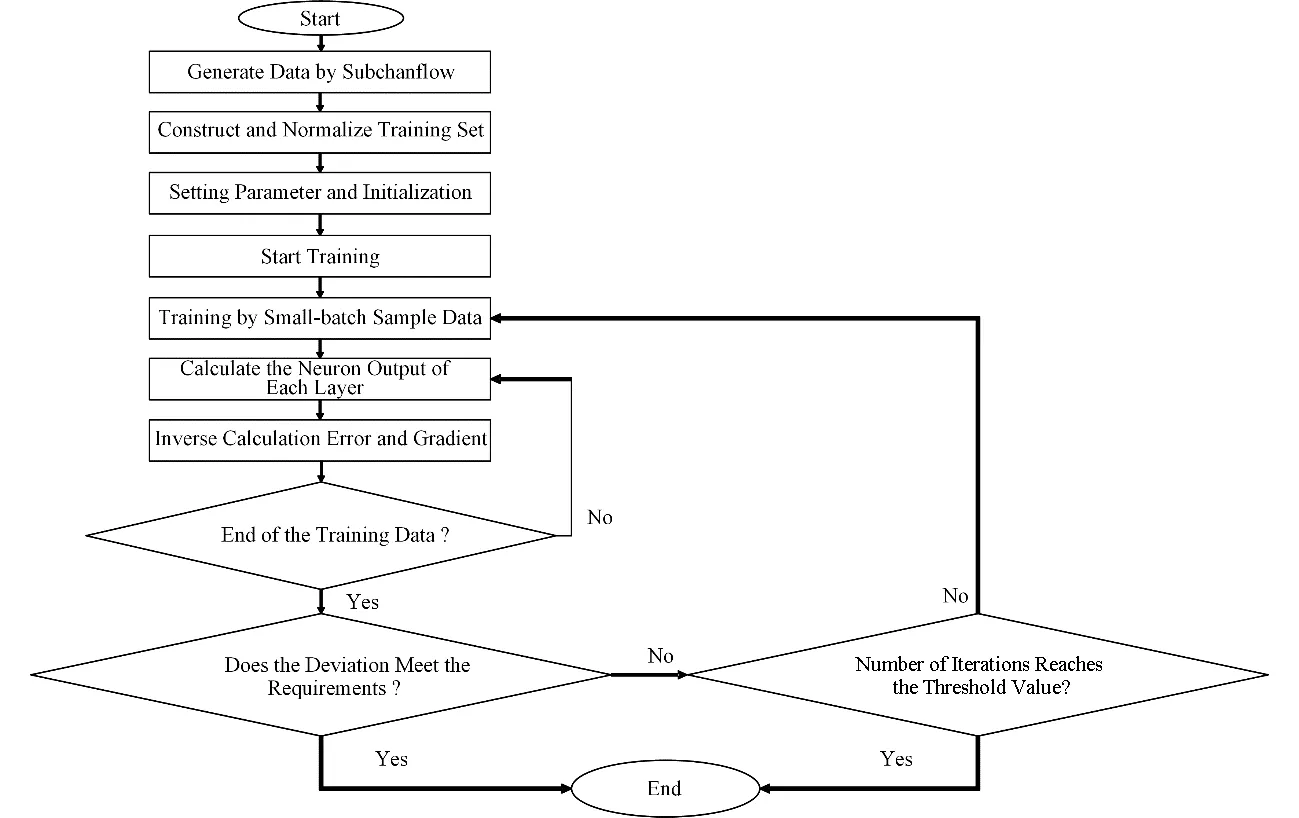
图3 神经网络预测模型流程图Fig.3 Flow chart of neural network prediction model

RBF神经网络隐含层的输入、输出为：

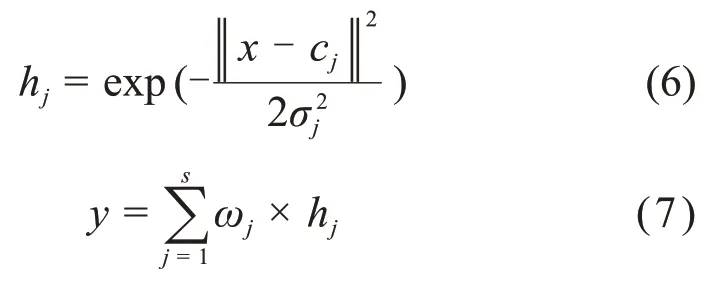
式中：cj为隐含层第j个节点的中心向量；‖x-cj‖为输入向量和中心向量间的欧几里得距离；σj为隐含层第j个节点的宽度；hj为隐含层第j个节点的输出，ωj为第j个神经元的权重；y为网络的输出。

RBF神经网络更新权值的实现步骤与BP神经网络相似。在完成单次训练后使用梯度下降法迭代每个神经元权重，达到终止条件后停止迭代并得到一组最优权值。RBF同样存在迭代过程中学习速率恒定的问题，因此本文中对广义RBF神经网络的参数选择以Adam自适应算法进行优化得到自适应RBF神经网络。

由上述分析可知，RBF相比于一般的BP算法的神经网络，泛化能力更好，学习收敛速度很快，这就使得其在非线性时间序列预测中有着更好的应用前景，针对这一点，下面分别研究了自适应BP神经网络与自适应RBF神经网络应用于堆芯关键热工参数的稳态与瞬态分析的相关性能。

2 不同神经网络模型对比分析

为对比不同神经网络模型的优劣，选用中国实验快堆（China Experimental Fast Reactor，CEFR）不同情况下的燃料包壳最高温度作为依据进行了对比。CEFR的主要热工参数如表1所示。CEFR平衡态循环时燃料组件燃料段功率及堆芯4个流量区的组件流量参考CEFR安全分析报告确定，具体数值如图4所示，其中第一行数值表示1/2全堆芯分析时子通道编号；第二行数值为燃料组件总功率，kW；第三行数值为子通道冷却剂流量，kg·s-1。

图4 堆芯分析通道编号、功率及流量分布Fig.4 Distribution of channel number,power and flow rate for core analysis

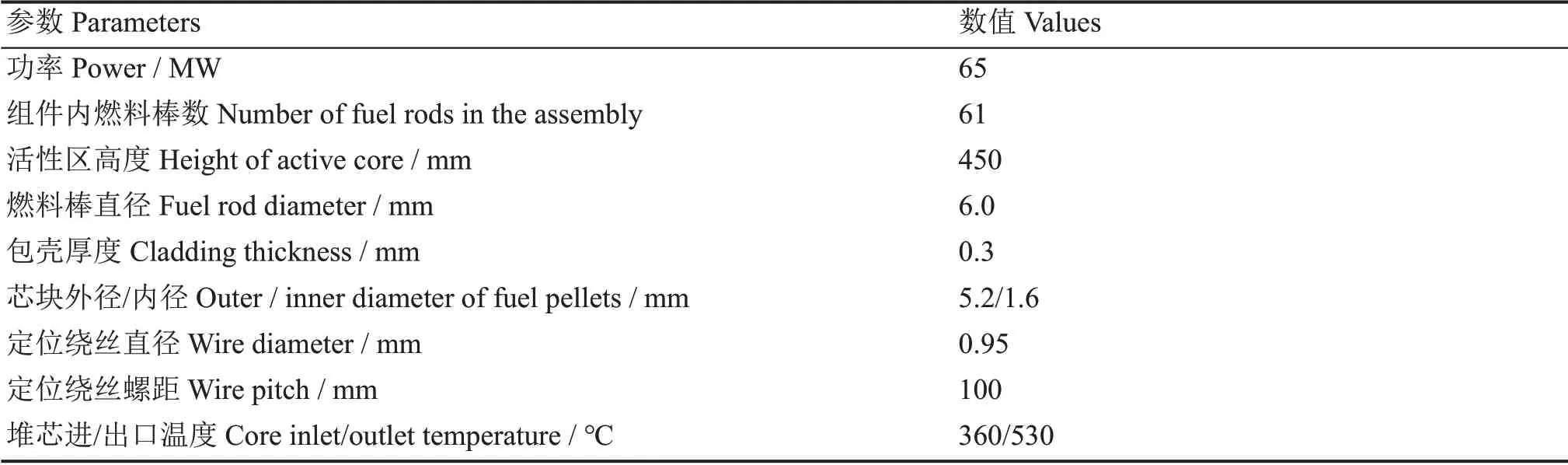
表1 CEFR的主要参数Table 1 Main parameters of CEFR

2.1 稳态单组件分析

反应堆正常运行下为稳态工况，出入口温度、流量等边界条件随时间变化不大，为简化模型可近似认为这些边界条件不变，研究稳定工况下的关键热工参数变化可进一步提高稳定工况下堆芯的安全性以及经济性。为探究两种神经网络对堆芯稳态工况下的预测性能，以CEFR堆芯为研究对象，进行稳态分析。使用神经网络进行预测分析可以分三部分：数据样本的获得、网络拓扑结构的确定和结果分析。

2.1.1 数据样本的获得

CEFR堆芯划分了4个燃料区，每盒组件内有61根燃料棒。使用Subchanflow程序［12］建立CEFR单组间模型时划分的子通道如图5所示，共划分了126个子通道。

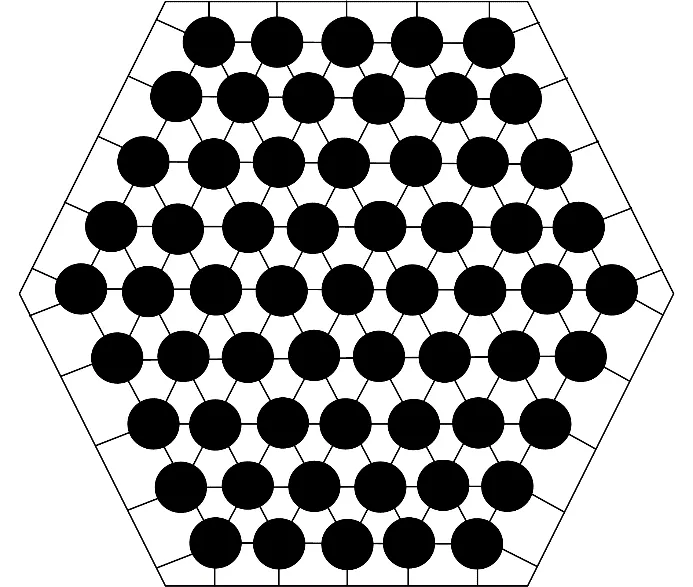
图5 冷却剂通道分布Fig.5 Layout of coolant channels

根据CEFR安全分析报告，CEFR的通道功率与流量范围为0～1 200 kW、0～6 kg·s-1，在该范围中任意选取若干组数据并结合表1中CEFR的主要参数填写Subchanflow的输入卡，通过程序计算后，最终得到1 000组有效数据样本。

自适应BP神经网络的预测泛化能力比较差，为此，可以通过增加验证集的方法来提高网络的泛化能力。将验证集增加到网络训练中，可以实时地监督预测误差的变化，当误差出现逐渐减小到增加的拐点时，可以停止网络的训练，并不再对网络权值进行更新。将数据集根据80%、20%划分为两部分［13］，训练集占80%，验证集与测试集共占20%，且样本数量相同。故从数据样本中随机选取数据样本中的800组数据作为训练集，100组作为验证集，剩余的100组数据为测试集。由于自适应RBF神经网络有良好的泛化能力与收敛速度，因此可以直接按照80%、20%的比例给出训练集和测试集合，所以在数据样本中随机抽取800组数据作为训练集，剩余的200组数据为测试集。通过测试集预测结果来构建评价模型。其中训练样本仅参与网络训练的过程，测试样本仅参与预测过程与结果分析。每次训练开始前均对训练集随机打乱顺序，从而尽量避免神经网络过多地记录局部特征。

2.1.2 网络拓扑结构的确定

在神经网络的学习中，隐含层数与隐含层节点数是其拓扑结构中非常重要的参数。过多的隐含层数会使得网络处于非稳定状态，并且随着隐含层数的增加会提高在训练过程中陷入局部最优的概率，而隐含层节点数过多会影响网络的学习时间，过少则会使得网络的学习结果很差甚至无法学习，除此之外隐含层数与隐含层节点数也与网络的泛化能力有关［14］，这些都会降低网络的整体性能。

Nielson通过理论证明过，对于只有一个隐含层层数的人工神经网络能够通过调整隐含层节点数逼近在闭区间连续的任何函数［15］，最终能够得到一个性能良好的网络。因此这里将两种不同的神经网络均确定为三层网络拓扑结构，即隐含层层数为一层，然后通过对每种神经网络不断地迭代计算来对隐含层节点数不断调试，根据网络的误差情况来确定出最终网络的最佳隐含层节点数。选取隐含层节点基本原则应该让网络的整体自由度与数据样本相当，故在［20，360］范围内每隔10个节点数选取为当前节点数，迭代5 000次，然后测试网络预测的平均相对误差，如图6所示。

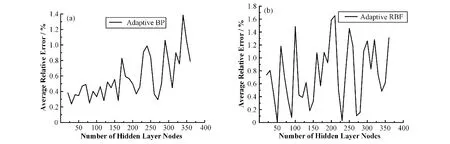
图6 隐含层节点数-平均相对误差曲线(a)自适应BP，(b)自适应RBFFig.6 Variation curve of average relative error with number of hidden layer nodes(a)adaptive BP,(b)adaptive RBF

由图6可以得到，在设定的节点数范围内，自适应BP的相对误差随着节点数目增多相对误差整体上呈上升趋势，因此选择最小平均相对误差时的节点数30；自适应RBF的平均相对误差随节点数的整体变化趋势并不明显，且节点数增加会增加网络学习时间，故选择随的隐含层节点为40。

2.1.3 结果分析

使用采用自适应梯度下降算法的BP神经网络、采用自适应梯度下降算法的RBF神经网络进行重复10次实验，统计测试集的预测结果并取平均，结果如表2所示。

表2 神经网络预测结果对比Table 2 Comparison of neural network prediction results

平均相对误差（Mean Relative Error，MRE）能反映数据样本的离散程度，MRE越小，总的预测效果越好，而最大相对误差能反映最大偏离实际值的程度，对局部数据的拟合能力。通过比较2种神经网络算法的测试集MRE与测试集最大相对误差，可以发现两种自适应神经网络的测试集MRE均小于1%，预测精度高，能出色地完成预测燃料包壳最高温度的任务，其中自适应RBF神经网络的最大相对误差小于1%，与测试集MRE十分接近，这表明其对于局部位置的拟合效果很好。

由上述结果发现，相比于自适应BP神经网络算法，自适应RBF神经网络对快堆堆芯内包壳最高温度的预测效果更好，能更出色地完成预测燃料包壳最高温度的任务。其原因是RBF神经网络模型相比于BP神经网络有更好的泛化能力，能够以更高的精度逼近任意复杂非线性函数，对于输入数据，能够获得精度较高的预测结果，具有良好的应用前景。

2.2 瞬态全堆分析

堆芯瞬态工况是由于事故或者冷却剂呈两相状态等原因导致冷却剂流量等堆芯热工参数会随时间发生较为明显的变化，进而影响堆芯的其他热工参数发生变化，其中流动不稳定性是对于瞬态下堆芯的安全性影响较大的工况之一，研究瞬态下的流动不稳定性对反应堆的安全运行有重要意义。瞬态工况下的神经网络构建方法与稳态工况相同。

2.2.1 数据样本的获得

使用Subchanflow构建1/2的CEFR堆芯全堆芯模型，为减少计算量，对堆芯子通道进行简化，假设燃料组件内各燃料棒具有相同的轴向与径向功率，将单个组件内所有的冷却剂通道合并成一个加热周长与润湿周长等效的燃料棒为中心的大通道［16］。为研究流动不稳定情况下神经网络的预测性能，向1/2的CEFR堆芯模型中输入的流量M（t）变化如图7所示，此数据由正弦信号和高斯白噪声信号叠加而成。经过计算得到堆芯燃料包壳最高温度T（t）变化如图8所示。

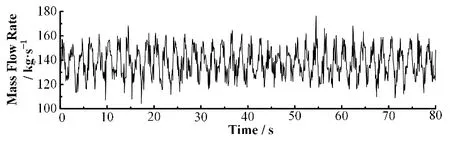
图7 堆芯入口流量变化Fig.7 Variation of core inlet flow

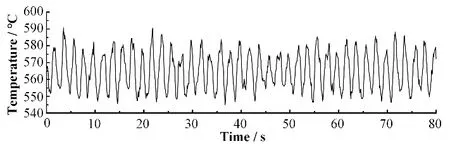
图8 包壳最高温度变化Fig.8 Variation of maximum cladding temperature

与稳态工况相比，瞬态工况下的参数预测由于冷却剂流量变化会引起其他热工参量都随时间发生变化，其数据处理会比稳态要更加复杂，为了方便预测，对流量时间序列和包壳最高温度时间序列进行相空间重构处理［17］：

其中，嵌入维度m取30，时间延迟τ取0.1。将相空间重构后的堆芯入口流量向量M（t）和包壳最高温度向量T（t）作为神经网络的输入，以两者的和作为输出，共得到771组数据，各数据集选择同稳态一致，故自适应BP神经网络训练集为541，验证集为115，测试集为115；自适应RBF神经网络训练集为617，测试集为154。随后分别使用两种神经网络进行了单步和连续预测（将预测结果依次替换输入向量进行预测），隐含层节点数的确定同稳态相同，在此不再赘述。

2.2.2 结果分析

使用自适应RBF神经网络进行单步预测和连续预测，并与测试值进行了对比，结果如图9、10所示。

由图9、10可以看出，对于堆芯入口流量的预测，当进行单步预测时，由于其本身含有较大的噪声，所以预测值的精度明显不如燃料包壳最高温度预测的精度，但是依然能够很好地反应堆芯入口流量的变化，而在连续预测中，由于预测值在下一次预测中会作为输入值进行预测，所以每次预测产生的误差会影响下一次的预测，图10中堆芯入口流量的连续预测值在前10 s内与测量值吻合得很好，在后7 s由于误差的累计，连续测量值与测量值出现了较大偏差，特别是流量振荡的波峰和波谷位置出现了偏移，可见长时间的连续预测预测精度显著降低，但是当只进行较短时间的预测时，堆芯入口流量的预测精度较高。

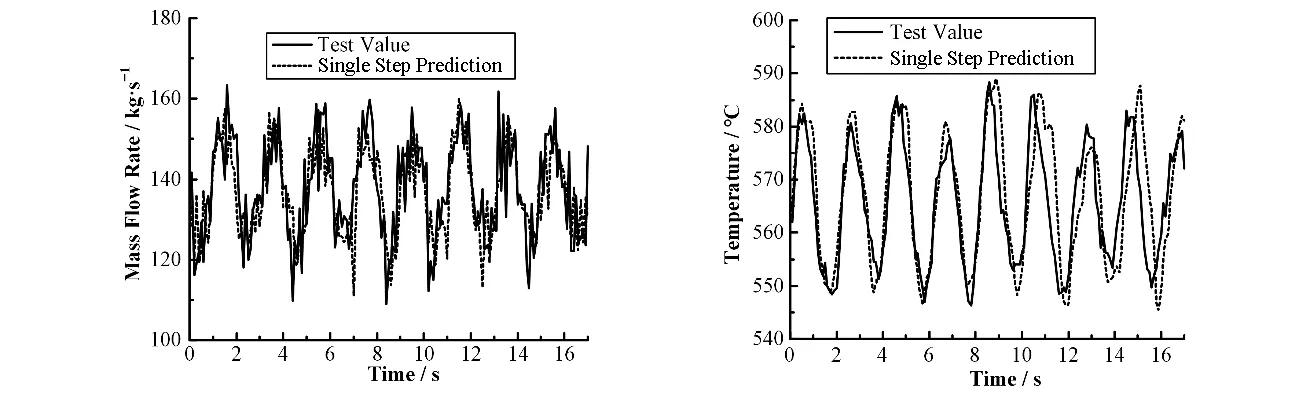
图9 测试值与单步预测值的比较Fig.9 Comparison of test and single step prediction values

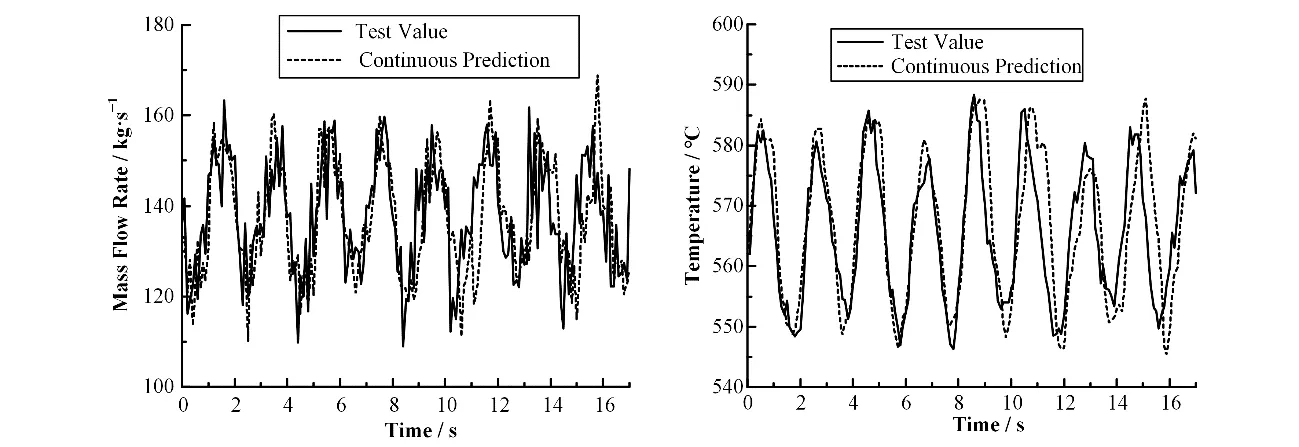
图10 测试值与连续预测值的比较Fig.10 Comparison of test and continuous prediction values

对于燃料包壳最高温度的预测，当进行单步预测时，预测值与测试值吻合很好，精度很高，而在进行多步连续预测时，前10 s的预测结果较好，而在后7 s由于堆芯入口流量的预测产生了较大偏差，影响了燃料包壳最高温度的预测，预测精度较差。

从以下结果可以看出，为了保证自适应神经网络预测结果的准确度，连续预测的时间步长需要得到限制，在较短时间的连续预测中，自适应RBF神经网络能够很好地完成燃料包壳最高温度的预测。

使用自适应BP神经网络和自适应RBF神经网络（以下简称BP神经网络和RBF神经网络）分别进行了单步预测和连续预测，预测结果列于表3。由表3可知，在相同的堆芯数据背景下，无论是BP神经网络还是RBF神经网络，单步预测的误差均小于连续预测的误差，但对于堆芯入口流量，由于其本身噪声的影响，使得单步预测平均相对误差和连续预测相比相差不大，对于包壳最高温度，单步预测误差明显小于连续预测误差。对比BP神经网络和RBF神经网络的预测精度发现，对于堆芯入口流量和燃料包壳最高温度的预测，RBF神经网络稍优于BP神经网络，其单步预测和连续预测的平均相对误差均小于BP神经网络。

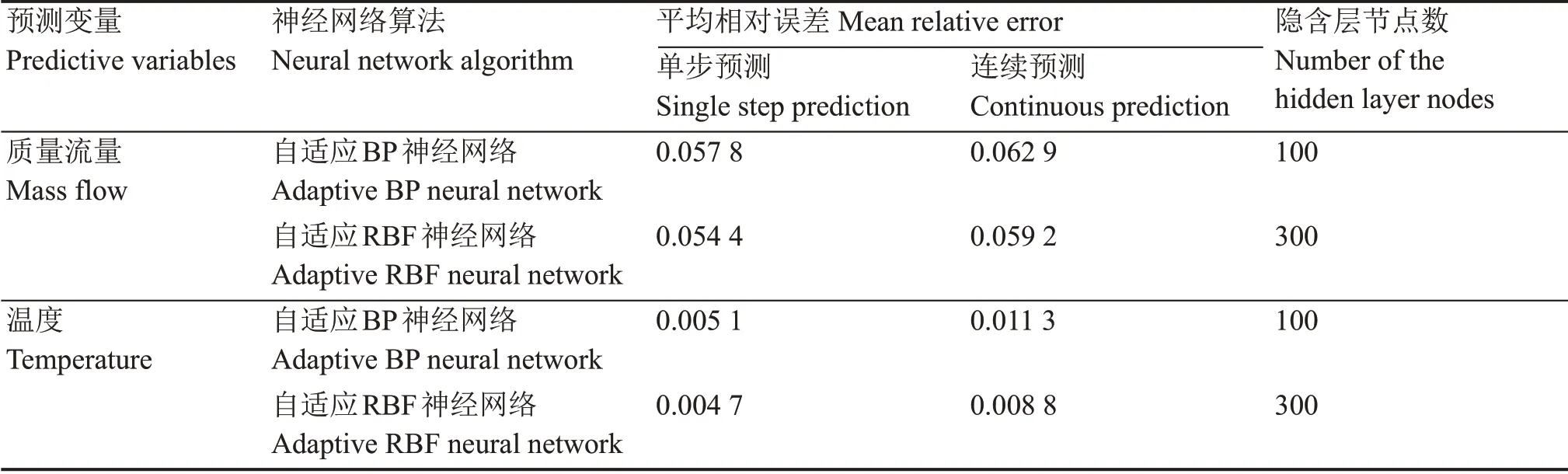
表3 神经网络预测结果对比Table 3 Comparison of neural network prediction results

3 结语

本文针对不同工况下CEFR燃料包壳最高温度以及质量流量预测问题，开展目前常用得两种自适应神经网络算法的分析对比，最终建立基于自适应RBF神经网络模型的反应堆稳态和瞬态热工参数预测方法，得到的主要结论如下：

1）选用CEFR燃料组件为研究对象，在相同的堆芯数据背景下开展反应堆稳态热工工况下燃料包壳表面最高温度预测分析，并对结果进行重复验证，结果表明，相比于自适应BP神经网络，自适应RBF神经网络具有更高的预测精度，其最大误差仅为0.5%。因此，自适应RBF神经网络算法在反应堆稳态工况下热工参数预测方面有着良好的应用前景。

2）选用1/2的CEFR堆芯为研究对象，开展反应堆瞬态热工工况下燃料包壳表面最高温度预测分析，并对结果进行重复验证，结果表明：相较于自适应BP神经网络，无论是单步预测还是连续预测，自适应RBF神经网络都有更好的预测精度，虽然由于其本身噪声的影响，存在个别局部点预测精度较差，但在总体上预测精度良好，其燃料包壳最高温度的预测平均相对误差不超过1%，而流量平均相对误差不超过6%。因此，自适应RBF神经网络能够在流动不稳定工况下提供较短时间的实时预测并保持一定的精度，这表明其在反应堆瞬态的实时预测上有较好的应用前景。

3）在堆瞬态工况的预测中，单步预测的误差精度在较长的时间内都是较高的，而连续预测的误差则只在较短时间内是可以接受的，随着时间增加，预测误差会逐渐变大，这是因为连续预测的误差相当于多次单次预测误差的叠加，要解决这个问题就需要对提高神经网络的单次预测精度做进一步地研究。

作者贡献声明冀南：神经网络算法设计，起草文章；易金豪：Subchanflow程序设计，获取CEFR堆芯的有效数据；赵鹏程：论文整体设计，数据分析，对文章作批评性审阅，研究经费支持，思想政治指导；于涛：对文章批评性审阅，研究经费支持。