路堤下混凝土桩复合地基抗桩体弯折破坏地梁效应

罗强，马宏飞，王腾飞，张良，蒋良潍

(1.西南交通大学土木工程学院，四川成都，610031；2.西南交通大学高速铁路线路工程教育部重点实验室，四川成都，610031)

随着社会经济的快速发展，高速公路和高速铁路大量兴建且建设周期不断缩短，现浇混凝土桩、钢筋混凝土桩、PHC桩[1]等刚性桩复合地基处理技术广泛用于软土地基加固。工程实践表明，刚性桩复合地基具有优良的抵抗沉降变形能力，一般能满足工后沉降控制要求，但其侧向抗弯折破坏能力较弱，在地形不利、高路堤等工程条件下的失稳事故时有发生[2]。

国内外学者开展土工离心模型试验[3−6]，发现刚性或半刚性桩复合地基路堤发生滑塌时，复合地基存在着多种破坏形式，如：受压破坏、剪切破坏、弯折破坏和倾覆破坏等；ZHENG等[7−9]的数值结果表明，路堤发生失稳时位于软土层的桩体中上部发生脆性弯曲破坏，并且桩体之间存在着渐进的破坏过程，复合地基中桩体的抗弯能力未得到完全发挥。

为增强桩体的横向抗力，NGUYEN 等[10]通过在水泥搅拌桩桩顶设置浅层承载板，使独立的桩体形成整体而提高桩体的水平抗滑力，有效地减小了软基沉降。KITAZUME 等[4]研究了在水泥搅拌桩桩顶设置约束对于提高路堤整体稳定性的影响。地梁是建筑基础的重要组成部分，通过约束桩顶的侧向变形从而增强基础的稳定性。近年来，路基工程逐渐引入纵横向正交连接的钢筋混凝土地梁作为刚性桩复合地基的横向加固措施[11]，YE等[11]通过在广东省兴汕高速公路汕尾段的某路基断面开展现场试验，研究发现地梁的设置能够大幅减小刚性桩复合地基的最大沉降、差异沉降以及侧向变形，但目前缺乏稳定性方面的分析，因此，对路堤下刚性桩−地梁复合地基整体稳定性进行系统研究，具有一定的工程实用价值。

数值分析方法可较好地考虑桩/土特性及路堤失稳的形式，近年来得到广泛的应用。在早期的研究中，NAVIN 等[12−15]利用基于Mohr-Coulomb 屈服准则的理想弹塑性模型来研究路堤下深层搅拌桩复合地基的破坏行为；YAPAGE等[16−18]利用基于Mohr-Coulomb 屈服准则的应变软化模型分析了水泥搅拌桩复合地基的渐进破坏行为。郑刚等[8]提出了1种可以表现刚性桩破坏性状的脆性拉裂模型来模拟混凝土桩的脆性拉裂行为，并给出了提高混凝土桩路堤稳定性的措施；俞建霖等[19]采用ABAQUS 软件中混凝土塑性损伤模型，研究了刚性桩复合地基中桩体的受力状态及破坏特征。

为研究路堤下混凝土桩复合地基抗弯折破坏的地梁效应，本文作者采用能有效描述混凝土材料裂缝张开和应力释放过程的Mohr-Coulomb tension crack(Mohr-T)模型，进行混凝土桩复合地基支承路堤的三维数值分析，模拟路堤下混凝土桩不均匀弯折破坏模式，分析不同桩顶约束下混凝土桩的破坏行为，讨论地梁加固措施对复合地基整体稳定性及混凝土桩受力的影响；开展参数化分析，掌握地梁材料强度和混凝土桩嵌入下卧土层深度对复合地基稳定性的影响规律。

1 Mohr-T模型

混凝土桩由于桩身强度高、延性弱等特点，桩体受弯开裂后不会形成塑性区[8]。为了描述混凝土桩拉裂缝产生及弯拉承载力削弱的过程，掌握路堤荷载下混凝土桩的弯折破坏机理，必须考虑混凝土桩脆性拉裂破坏前后的力学行为。本文采用的Mohr-T 模型可有效描述混凝土产生张拉裂缝时的力学响应。

1.1 控制方程

Mohr-T 模型是1 种与剪切流动法则不相关、与拉伸流动法则相关的Mohr-Coulomb 模型，在拉伸塑性屈服后，其抗拉强度及主应力会发生相应的变化。Mohr-T模型假设1个单元中至多同时有3条相互垂直的裂缝且均贯穿整个单元，当单元发生拉伸塑性屈服时，破坏准则满足式(1)。

式中：σ1，σ2和σ3为主应力，且σ1≥σ2≥σ3；σt为抗拉强度。Mohr-T模型需满足以下假设：

1)拉裂缝垂直于拉伸主应力σ1；

2)将垂直于裂缝方向单元的抗拉强度σt调整为0 MPa，模拟裂缝的张开和应力释放过程；

3)单元发生拉伸破坏后应力重新分布，垂直于裂缝方向的法向应力设置为0 MPa，产生拉伸塑性因子λt；

4)拉伸塑性应变εp1由λt累加而得，即Δεp1=λt。

1.2 破坏准则和流动法则

Mohr-T 模型采用考虑拉伸断裂(tension cutoff)的Mohr-Coulomb 综合破坏准则，如图1所示，破坏包络线f(σ1,σ3) =0 分为2 部分，AB段由Mohr-Coulomb 破坏准则定义，fs按式(2)计算，BC段由拉伸破坏准则定义，ft按式(3)计算。

式中：φ为内摩擦角；c为黏聚力；参数Nφ=(1+sinφ)/(1-sinφ)。

材料的抗拉强度σt不能超过(σ1,σ3)平面中直线fs=0 与直线σ1=σ3的交点，抗拉强度最大值为

势函数由剪切塑性流动函数gs和拉伸塑性流动函数gt描述。gs函数对应非关联流动法则，gt函数对应相关联流动法则，分别按式(4)和式(5)计算。

式中：ψ为膨胀角；参数Nψ=(1+sinψ)/(1-sinψ)。

1.3 计算参数确定

Mohr-T 模型中混凝土材料的抗剪强度参数黏聚力c和内摩擦角φ可由图2所示的方法确定。

1)参照既有研究及振动混凝土桩的现场测试数据，确定混凝土桩的轴心抗压强度f′c；

2)根据美国混凝土协会(ACI)的建议，混凝土材料的弯拉强度f′r可通过跟轴心抗压强度f′c的关系确定，按下式计算：

3)如图2所示，通过A点与B点可以确定服从Mohr-Coulomb 破坏准则的破坏包络线，从而定义混凝土桩体的黏聚力c和内摩擦角φ。其中A点在大的应力圆中，代表在无侧限抗压试验中测得的轴心抗压强度f′c；B点位于小应力圆之上，故拉伸破坏会早于剪切破坏发生，代表的是弯曲拉伸试验中的应力状态，其正应力σ在数值上等于弯拉强度f′r，剪应力τ为弯拉强度f′r的1/2；

4)考虑到半幅路堤模型中桩体的网络划分精度与单桩网络划分精度的差异，即：在网格密度较密的单桩模型中侧向施加均布荷载直至桩身出现拉裂破坏，再将同样的破坏荷载作用于网格较疏的复合地基计算模型桩体上，得到桩体实际的抗拉强度σt。

1.4 3点弯曲梁试验验证

为验证Mohr-T 模型描述混凝土发生弯折破坏时脆性断裂行为的可靠性，采用图3(a)所示的混凝土3点弯曲梁试验[20]进行验证，图3(b)所示为计算值和试验值的对比。为较好地反映试件裂纹的扩展过程，数值模拟采用位移控制法。3点弯曲梁试验中，试件宽度b=38.1 mm，高度d=76.2 mm，试件的弹性模量E=27 500 MPa，泊松比ν=0.2，轴心抗压强度f′c=30 MPa，抗拉强度和抗剪强度按1.3 节方法求取，得抗拉强度σt=2.9 MPa，黏聚力c=3.93 MPa，内摩擦角φ=47°。

由图3(b)可知：基于Mohr-T 模型的模拟结果表明，在位移小于0.1 mm 时，极限荷载随变形增加而增大，随后由于混凝土中形成拉裂缝而造成试件抗弯承载力急剧下降，这与Baz˘ant-Luzio的试验结果吻合[20]，可知Mohr-T 模型能合理地模拟混凝土材料裂缝的发展和发生弯折破坏后的应变软化现象。

1.5 混凝土桩复合地基模型验证

为验证Mohr-T 模型对模拟混凝土桩复合地基行为的合理性和准确性，本文基于FLAC3D软件建立三维模型，如图4(a)所示，其中混凝土桩使用Mohr-T 本构模型。对于路堤稳定性而言桩体抗弯能力是主要因素，为提高计算效率，根据抗弯刚度等效原则把圆形管桩等效为方桩。根据郑刚等[21]开展的离心模型试验中的桩体参数，数值模型[22−23]中桩体容重取27 kN/m3，弹性模量为78.7 GPa，泊松比为0.3，极限抗拉强度为10.8 MPa，综合抗剪强度为25.1 MPa[24]。采用Mohr-Coulomb 理想弹塑性模型对路堤填土及地基土进行模拟，桩土界面抗剪强度取值为相邻土体的2/3[25]，桩土相对滑移后界面强度不变，界面法、切向刚度均为10 GPa/m[25]。根据土工离心试验条件，逐级调整数值模型的重力加速度模拟离心加载过程，将数值计算模型的结果与郑刚等[21]所提方案5中的试验数据进行对比。

数值计算模型中土体的计算参数如表1所示，图4所示为路堤失稳时混凝土桩复合地基的破坏变形图及路堤监测点的竖向沉降位移曲线。

与离心模型试验结果对比可知，复合地基破坏变形大致相同(图4(b)和4(c))，路堤监测点处的离心加速度−沉降位移曲线相近(图4(d))，桩体采用Mohr-T 本构模型能够考虑弯折破坏造成的拉裂缝，与离心模型试验结果吻合度较高。因此，本文使用的Mohr-T 模型基本可以合理反映复合地基的变形特性，准确模拟混凝土桩复合地基实际工作状况。

2 三维计算模型

2.1 路堤及复合地基结构模型

为探讨地梁对复合地基支承路堤稳定性的影响，采用有限差分软件FLAC3D建立如图5所示的三维路堤模型，计算模型依据JTG B01—2014“公路工程技术标准”的规定，选用典型的双向四车道高速公路路基断面尺寸，根据对称性取路基宽度的一半进行研究。模型几何尺寸沿路基横断面方向取93.6 m，沿线路纵向取桩的布置间距，为3.0 m，垂向总高度为32 m。其中，路堤高为5 m、黏土层厚度为15 m、砂土层厚度为12 m，路基面宽为24 m，路堤边坡坡率为1.0:1.5；复合地基中的混凝土方桩截面边长为0.4 m，长为19 m，采用正方形布置，地梁截面同混凝土方桩，由于本文研究的侧重点为稳定性问题，故地梁沿混凝土桩顶横向的通长布置不考虑纵向连接，如图5所示。计算模型的两侧面约束水平方向线位移、底面约束水平和竖直方向线位移。

2.2 土体与桩梁材料模型及计算参数

路堤填土、地基软黏土和砂土均采用服从Mohr-Coulomb 屈服准则的理想弹塑性模型[22]，路堤快速填筑及加载过程中，不考虑地基土体的排水固结。混凝土桩和地梁为现浇C20混凝土，采用Mohr-T 本构模型，根据GB 50010—2010“混凝土结构设计规范”确定材料剪切强度、黏聚力c、内摩擦角φ=0°[22]及弯拉强度ft。桩土接触面单元使用Coulomb剪切强度准则的线性模型，相关参数参照1.5节验证案例。路堤及地基土体性质见表1。

表1 模型中的桩土材料计算参数Table 1 Model parameters of piles and soil mass

2.3 主要计算步骤

1)通过调整混凝土桩及地梁单元的材料参数为桩梁结构周边土体参数，模拟地基的初始应力状态，再将相应的混凝土桩梁单元变更为混凝土材料参数，模拟地梁−混凝土桩复合地基空间结构初始状态；

2)路堤分5层逐级模拟填筑，每层厚度1 m；

3)路堤模拟填筑完成后，在路基面以1 kPa为1 级逐级施加均布荷载q，分析路堤荷载增加对复合地基侧向变形及应力应变等力学响应的影响。

4)在路堤自重荷载p=γh及路基面超载q作用下，路堤坡脚水平变形大幅增加，计算不收敛时认为达到极限状态，对应的路堤超载为极限加载qu，采用强度折减法计算复合地基支承路堤的稳定安全系数。

3 复合地基地梁效应分析

3.1 对混凝土桩复合地基稳定性影响

图6所示为路堤坡脚水平位移与路堤超载的变化曲线。其中，无地梁工况下qu=56 kPa，路堤稳定安全系数FS=1.53；设地梁工况下qu=141 kPa，对应的路堤稳定安全系数FS=2.32，提升幅度高达52%。

图6中超载为0 kPa 表示路堤填筑完成时的状态，此时无地梁工况下的路堤坡脚水平位移为62 mm，而地梁工况下位移减少了约81%，即12 mm。在q<56 kPa时，路堤坡脚水平位移随荷载增加逐渐增大，且标准工况下位移增加速率比设置地梁工况下的快：q从40 kPa增至50 kPa时，无地梁工况位移增加了38.4 mm，而设置地梁工况的位移仅增大了3.4 mm。这说明在混凝土桩顶位置设置地梁，能有效降低路堤荷载作用下的复合地基水平变形。图6中，路堤超载与坡脚水平位移曲线出现突变现象，反映了混凝土桩在极限荷载作用下发生脆性断裂的特性。

图7所示为路基结构失稳时2种工况下的水平位移云图及混凝土桩拉裂破坏位置分布图，其中黑色表示混凝土单元发生开裂。当qu=56 kPa 时，无地梁工况下坡脚水平位移急剧增大，路堤下复合地基失稳滑塌，混凝土桩的中上部及软硬土层交界面位置出现多处混凝土单元拉裂破坏，甚至贯穿整个桩截面，使得桩体发生较大弯折变形，失去抗弯能力；对于设置地梁工况，只有1 号和2号混凝土桩顶与地梁连接处出现小范围拉裂，地基中不同部位设置的混凝土桩其余部分均未伤损，路堤仍处于稳定状态，地梁对混凝土桩的横向约束作用较强，直到qu=141 kPa，位于路堤中心下地梁受拉断裂，地梁与混凝土桩连接处达到抗拉强度后发生断裂，地梁失去对桩体的约束作用，导致桩体侧向位移过大，路堤随即失稳破坏。

在无地梁工况中，混凝土桩中上部的桩间土水平位移较大，混凝土桩承受较大水平推力，产生弯折断裂，复合地基易发生失稳滑塌。通过在桩体顶部架设地梁，可以减小桩体水平方向差异性变形，使得不同位置桩体能同时发挥抗弯能力。此外，设地梁工况的地基土滑动面下切深度更小，说明地梁的布设强化了桩群的整体性，增加了地基加固体整体水平刚度，显著提高了路堤下复合地基抗水平变形能力，不易出现路堤失稳现象。

3.2 混凝土桩受力特性

3.2.1 降低弯拉应力

当混凝土桩中某单元的最大拉伸主应力即拉应力达到极限抗拉强度时，混凝土单元会产生1条垂直于弯拉应力的裂缝。混凝土单元弯拉主应力减至0，意味着该桩体单元产生裂缝，且发生了弯折破坏。以位于路堤坡脚附近的最先发生弯折破坏的2号混凝土桩为例，桩体截面单元弯拉应力沿深度分布，在发生弯折破坏前后的对比如图8所示。

由图8可知：q=56 kPa 时，无地梁工况中2 号混凝土桩在软黏土和砂土交界面处开裂并发生弯折破坏，随后2号混凝土桩的截面弯拉应力重新分布，最大值从砂土层顶面位置的15 m 上升至软黏土层中8 m 深附近，达到了混凝土的极限抗拉强度，桩身产生开裂破坏；同时，相邻的1号和3号桩桩身的弯拉应力接近极限抗拉强度，分别为1.32 MPa和1.24 MPa，桩身极易开裂；随后，2号混凝土桩在软黏土层中部发生脆性断裂，导致该桩体完全丧失阻止地基滑动的能力，由2号桩中部截面断裂所释放的应力，依次引发1号桩和3～6号桩体的中部发生断裂破坏。从图6可知：路堤坡脚水平位移−超载曲线发生突变，复合地基最终发生了滑动破坏。

对于地梁工况，当q增加至56 kPa，2 号桩顶部位置的压应力有所增加，设置地梁后桩体沿深度方向分布的拉伸主应力大幅减小，除了1号桩的最大弯拉应力达到0.4 MPa外，其余各桩最大弯拉应力均为负值，即以承担竖向的压应力为主，弯拉应力远低于混凝土的抗拉强度，各桩可稳定发挥抗滑移作用，复合地基处于稳定状态。对比可知，混凝土桩顶部设置地梁能大幅减小混凝土桩承受的弯拉应力，显著提高复合地基的稳定性。

3.2.2 减小弯矩

图9所示为路堤顶面超载q=56 kPa时，布设地梁前后混凝土桩的弯矩分布曲线。对比图8可知：未设置地梁时，在路堤发生失稳破坏前，2号桩的弯拉应力8 m深附近达到极限抗拉强度，故1号和2 号桩此处对应的弯矩大幅增加，峰值分别为26 kN·m 和37 kN·m；由于1号和2号桩在软硬土层交界面处已经发生弯折破坏而使弯矩降至0 kN·m，说明混凝土桩体开裂后桩身应力发生释放，截面开裂处承担的弯矩降低；同时3号和4号桩在软硬土层交界面处的弯矩超过80 kN·m，接近桩体极限抗弯承载力；处于路堤中心下的7号混凝土桩的最大弯矩仅为0.1 kN·m，说明中间桩体主要承担竖向荷载，如图9(a)所示。

在图9(b)所示地梁工况中，所有桩体弯矩分布曲线未出现明显波动和弱化，桩身不存在拉伸损伤。1～5号混凝土桩与地梁连接处达到桩身弯矩峰值，其中2号和3号桩在连接处弯矩较大，分别达到55和54 kN·m，桩深4 m以下位置的弯矩均小于无地梁工况中对应的弯矩，设置地梁工况中每根桩体弯矩曲线分布规律和数值都非常接近，说明地梁具有减小混凝土桩体弯矩和缩小桩间弯矩差异的力学效应。

3.2.3 增大轴向压力

路堤下复合地基中不同位置处混凝土桩的弯拉应力和弯矩在空间上分布不均匀，而决定桩体中混凝土单元开裂破坏的弯拉应力受弯矩和轴力共同控制。因此，不同位置处混凝土桩的轴力分布也具有空间不均匀性，如图10所示。从图10可知：此时2种工况中路堤顶面超载均为56 kPa。轴力负值代表桩体受到拉力的作用。

由图10可知：沿路堤坡脚至路堤中心方向各桩轴力逐渐增大，位于路堤坡脚下的1号混凝土桩轴力最小，位于路堤中心下的6号混凝土桩轴力最大。在软黏土层中，由于桩体与桩间土存在相对位移，产生负摩阻力；在砂土层中，桩体相对于砂土层向下移动导致轴力随桩深增加而减小。未设置地梁时，1 号桩在0～8 m 深度范围内存在拉力作用，有上拔趋势，与文献[7]中一致；结合图9和图10可知，路堤荷载作用下2号桩由于轴力较小和中部弯矩较大，导致桩体中部的弯拉应力迅速超过抗拉强度，进而出现弯折破坏。地梁的刚度较大，可将大部分的路堤荷载均匀地分配到不同位置处的混凝土桩，显著提高了桩体承受的轴向压力，1～7号桩的轴力平均提高了174 kN，有效降低了混凝土单元的弯拉应力，改善了桩体的受力特性，对避免混凝土桩发生弯折破坏有着积极作用。

3.2.4 减小桩间土附加应力

桩间土附加应力定义为在路堤荷载作用下地基土产生的竖向应力增量，是引起地基失稳的关键因素。本文以路肩下3号桩体为研究对象，分析不同路堤顶面超载作用下桩间土附加应力的变化情况，如图11所示。从图11可知：桩间土附加应力随路堤超载增加而增大；附加应力沿地基土深度衰减，在地基表面达到峰值。对于无地梁工况，桩间土附加应力在地基土层中的传递深度与路堤荷载水平相关，路堤荷载越大附加应力的衰减程度越小，当路堤荷载增至56 kPa 时，复合地基支承路堤失稳，桩间土附加应力较上级荷载明显增加。此外，桩顶布设地梁后，地基表层桩间土的附加应力显著降低，并且在路堤顶面施加相同超载幅值后，桩间土附加应力仅有小幅增加，外部荷载的变化对附加应力影响甚微。由此可见，桩梁结构能有效减少桩间土附加应力，防止软土地基因附加应力过大而发生失稳破坏。

综上可知，在复合地基中的混凝土桩顶设置地梁，可使混凝土桩承受更多上覆路堤荷载，有效增加桩体轴向压力，减小桩间土的竖向和水平荷载，降低水平方向的桩土相互作用，减小不同位置桩体的弯矩绝对值和相对差值，从而减小桩体的弯拉应力，能充分发挥混凝土桩的抗压强度高、而抗拉强度低的力学特点。同时，布设地梁可减少桩间土附加应力，避免桩间软土发生滑动破坏，对提高路堤下混凝土桩复合地基的整体稳定性效果明显。

4 参数分析

分析混凝土桩复合地基支承路堤失稳案例[6,10]，发现桩体长度是影响复合地基稳定性的重要因素。设置地梁后的混凝土桩复合地基桩体也可能产生过大水平位移，从而导致路堤失稳。充足的桩端嵌入深度有利于增强整体稳定性。为进一步分析地梁措施对混凝土桩复合地基整体稳定性的影响，针对3种等级混凝土桩/地梁和5种桩端嵌入深度，开展混凝土强度和桩长2个因素的参数化分析。计算方案及结果见表2和图12，其中，Le为嵌入地基砂土层深度，L0为地基软黏土层厚度。

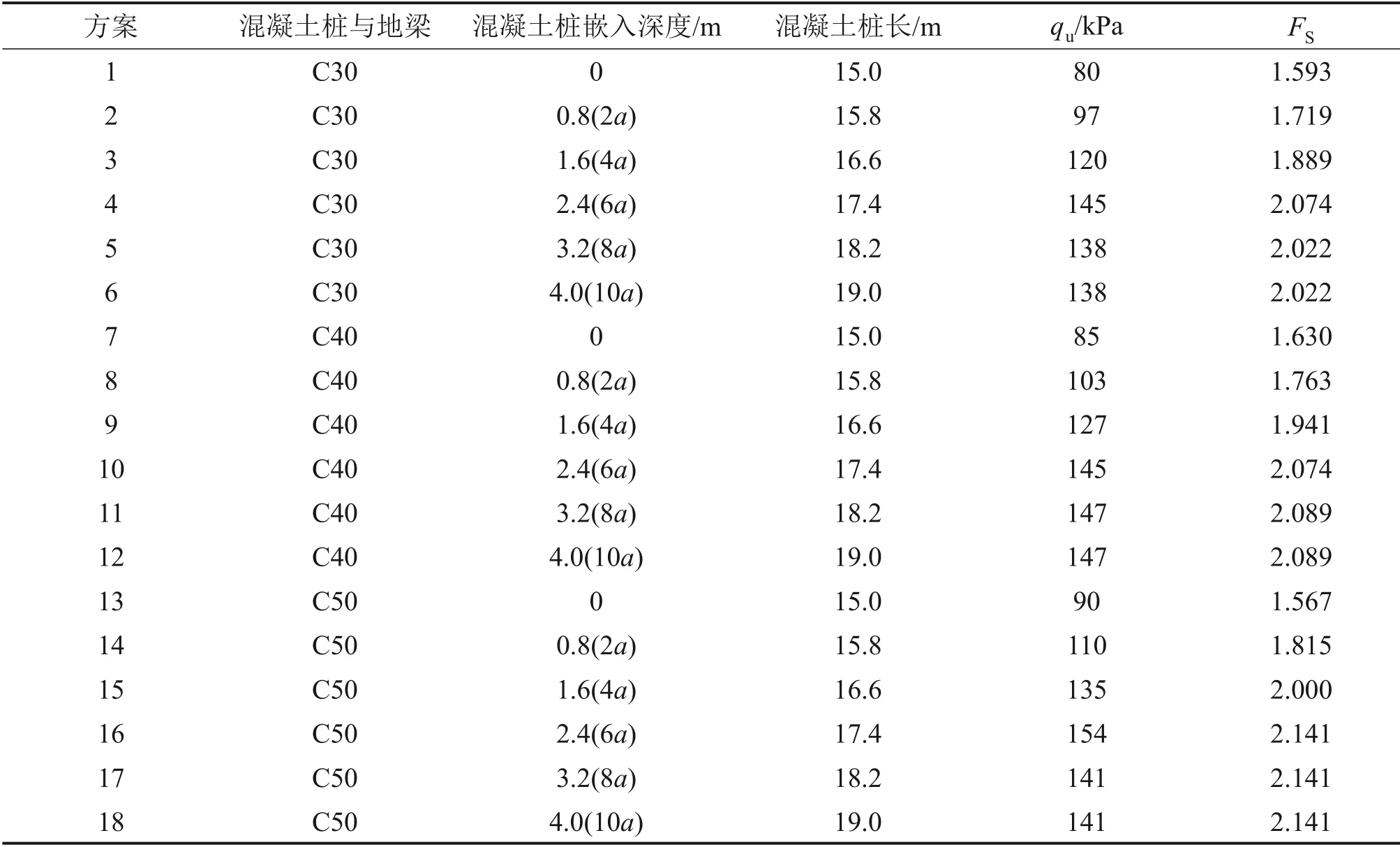
表2 计算方案及结果Table 2 Simulation scenarios with results

由图12可知：采用高强混凝土和增大桩长，均能不同程度地提高复合地基的抗滑稳定性。需要注意的是，将混凝土桩及地梁的强度等级分别从C30提高至C40及由C40提升到C50，复合地基的稳定安全系数仅提高约2.33%和2.27%，效果并不显著。这是因为同时提高桩和地梁混凝土等级时，相当于提高了地梁极限抗弯能力Mu，而地梁的抗弯刚度也相应增加，混凝土地梁弯矩增大，导致地梁弯拉应力增大，更易发生弯折破坏，不能有效增强地梁对桩体的约束作用，从而提高复合地基的整体稳定性。

当嵌入深度Le从0 m 增至2.4 m 时，复合地基支承路堤的稳定安全系数随嵌固深度增加近似呈线性增长，稳定安全系数约提高30%，加固效果显著；当Le超过2.4 m后，稳定安全系数基本保持稳定，表明混凝土桩嵌入下卧土层的深度存在1个临界值。当嵌入深度从0 m 增加至2.4 m 时，持力层对桩体的桩端约束逐渐加强直至接近刚性约束，使得桩体不会绕桩底作刚体转动；而嵌入深度大于临界值后，持力层不能继续增强对桩端的约束作用。故过大的嵌入深度既不能有效提高地基的稳定性，也会增加施工难度，造成浪费。

综上，使用混凝土桩−地梁复合地基支承较高路堤时，宜选择较强混凝土材料并适当配筋，保证地梁强度的同时也能增强地梁与混凝土桩连接部位的抗弯能力；混凝土桩需确定合理的嵌入下卧较硬土层锚固深度，在增加复合地基稳定性的同时保证良好的经济性。

5 结论

1)Mohr-T 模型能够表征混凝土桩体的脆性弯折破坏模式，模拟混凝土桩断裂后应力转移和桩土应力重分布的过程，真实地反映混凝土桩复合地基支承路堤失稳破坏的特点。数值结果与3点弯曲梁试验及离心模型试验结果吻合，验证了模拟方法的可靠性。

2)混凝土桩复合地基的破坏具有不均匀性和渐进性；位于路堤坡脚下的桩体承受较小轴力和较大弯矩，易率先发生弯折破坏，桩体截面断裂释放应力导致相邻桩体弯矩增大，随着路堤荷载增大，由坡脚往路堤中心方向发生连续弯折破坏，最后形成塑性滑面导致整体失稳；桩体中部的弯折破坏为控制路堤稳定性的关键。

3)布设地梁有利于发挥混凝土桩材料特性，有效约束桩顶水平变形，使不同位置处桩体峰值弯矩降低约40%，减小不同位置桩体弯矩的差异，充分发挥路堤中心下桩体的抗弯能力；使桩体轴力增大约170 kN，桩身弯拉应力水平低于抗拉强度，较好发挥桩体的抗滑功能；此外，地梁结构可大幅减小桩间土附加应力，避免地基软土因变形过大而破坏。

4)混凝土强度和桩端嵌入深度与复合地基的稳定安全系数近似呈正相关，但桩端嵌入深度的提升效果更显著；桩端嵌入深度存在临界值，若嵌入深度超过该临界值时，复合地基的整体稳定安全系数并无明显提升，故嵌入深度取2～3 m时能为桩体提供充足的桩端约束以抵抗土体水平滑动。