波浪作用下软黏土海床动力响应离心模型试验
2022-09-21吴雷晔万佳怡孔德琼朱斌陈仁朋陈云敏
吴雷晔,万佳怡,孔德琼,朱斌,陈仁朋,陈云敏
(1.浙江大学软弱土与环境土工教育部重点实验室,浙江杭州,310058;2.浙江大学岩土工程研究所,浙江杭州,310058;3.浙江大学超重力研究中心,浙江杭州,310058)
波浪是海洋中常见的物理现象,也是海工结构物设计中需考虑的重要因素之一。在水深较浅的近海区域,波浪除直接作用于海工结构物外,其在海床表面形成的循环波压力会导致海床内部超静孔隙水压力上升和有效应力降低,进而影响海床周围海工结构物如单桩、管道等的承载力及稳定性。
目前,对于波浪作用下海床动力响应的研究主要集中于无黏性土。在理论方面,早期主要基于Biot 固结理论和多孔弹性模型对海床内部土体在波浪作用下的瞬时响应进行研究[1−3]。而对于波浪作用下海床内部的超静孔隙水压力累积,通常采用2种方法进行评估:一是在控制方程中引入反映超静孔隙水压力增长的源项[4−5];二是基于弹塑性土体本构模型,计算相应的土体塑性变形及孔压累积[6−7]。在试验方面,常重力下的水槽造波试验是常用的手段,例如PAN 等[8−9]利用造波水槽研究了粉质、砂质海床在波浪作用下的响应及其对海底管道的影响;SASSA 等[10]采用搭载于土工离心机的摇板式造波实验装置对松散砂质海床在波浪作用下的液化和重固结现象进行了离心模型试验研究,为涉及波浪荷载的土工物理模拟试验提供了新思路。
相较于无黏性土,人们对波浪作用下软黏土海床动力响应的研究较少。一些学者通过室内单元体试验模拟土体在波浪作用下的应力路径[11−13]。DE WIT等[14−15]采用室内造波水槽对软黏土海床在波浪作用下的动力响应进行了试验研究,观测到了明显的孔压累积和表层海床运动现象;闫澍旺等[16]通过控制水压的方式在离心机中模拟了软黏土对波浪荷载的响应,发现波浪作用会导致软黏土海床强度降低。软黏土广泛分布于我国沿海地区,许多重要的海洋工程都建设在软黏土地基上[17]。这些软黏土具有孔隙比大、强度低、压缩性高、渗透性低、灵敏度高等特点,在波浪作用下,会发生超静孔隙水压力累积,从而导致承载力大幅降低的现象。在此过程中,海床表层原本呈现固态性质的“土”将转换为流态化的“泥”,而其中的规律尚未被充分研究。此外,针对软黏土海床的模型试验研究大多采用常重力下的水槽造波方式,虽然能够较好地模拟波浪作用下模型海床土体响应的时空分布规律,但由于模型尺度较小、试验历时较短,对现场典型波浪工况下海床响应的模拟尚存不足。
造波离心模型试验具有缩尺缩时效应以及弗劳德数无条件相似的特点,通过模型试验可以再现现场时空尺度下波浪对海床的作用过程,近年来受到研究者们的广泛关注[18−20]。本文采用浙江大学自行研制的机载波浪模拟实验装置开展离心模型试验,对波浪作用下软黏土海床动力响应进行研究,分析波浪加载−重固结过程中海床内部孔隙水压力的时空响应、海床表面位移以及海床强度变化。
1 机载波浪模拟实验装置
1.1 总体介绍
基于浙江大学已建装置[21]对机载波浪模拟试验装置进行改进,其实物图如图1(a)所示。其中,模型箱内侧长×宽×高为1.3 m×0.4 m×1.0 m,在模型箱前侧装有透明有机玻璃,以便观测试验过程。在机载波浪模拟试验装置中,将伺服电机从模型箱端部改装至中部,以缩短传动距离,将曲柄连杆传动机构改造为导轨−滑块传动机构,以增加其运行过程中的稳定性,如图1(b)所示,连接于导轨−滑块传动机构的摇板式造波板,设置在造波模型箱另一端、用于减少模型箱侧壁的反射波对试验影响的可移动格栅式吸波板,模型箱内中部用于放置模型海床的凹槽保持不变。

图1 机载波浪模拟试验装置Fig.1 Wave-loading system used in centrifuge test
1.2 造波模块
在机载波浪模拟试验装置中,造波模块主要依据HUGHES[22]推导的实验室造波理论设计,通过伺服电机经由传动机构带动造波板前后摆动推动水体,从而模拟规律正弦波浪。造波模块示意图如图2所示。图2中,h为水深,H为波浪高度,s为造波板划水距离,L为波长,l为造波板下端铰接点距泥面高程的垂直距离(本装置中设为0.03 m)。

图2 造波模块示意图Fig.2 Schematic diagram of wave maker
当水深h和造波频率f确定后,波浪高度H与造波板划水距离s(造波板在静水位处摆动幅值的2倍)的关系可由下式确定[22]:
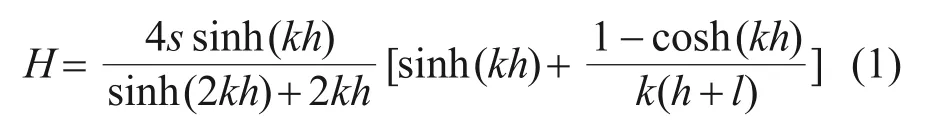
式中:k为波数,k=2π/L。
由线性弥散方程可得

式中:g为重力加速度;N为比例系数;ω为波浪圆频率,ω=2π/T,T为波浪周期(T=1/f)。
根据线性波理论,波浪在泥面处产生的压力幅值p0为
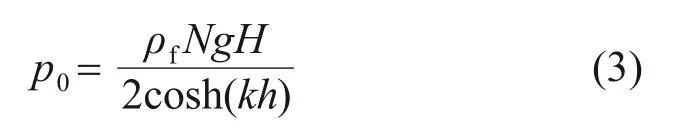
式中:ρf为水的密度。
以重力加速度20g,连接轮盘直径0.12 m 为例,不同水深和频率下泥面处的波压力幅值p0如图3所示。其中,划水距离s可根据造波板铰接点距连接轮盘高程距离(0.48 m)以及连接轮盘直径和水深换算得到。

图3 不同水深和频率下泥面处波压力幅值Fig.3 Amplitude of wave pressure at mudline under different depths and frequencies
1.3 吸波模块
在试验过程中,由于模型箱长度有限,当波浪触及到另一侧模型箱侧壁时会发生反射,反射波与入射波叠加导致实际波浪与目标波浪特性不同,因此,需要采取合适的吸波措施以减少反射波的影响。本装置采用设置在模型箱一侧的格栅板进行被动吸波,如图1(b)所示。当波浪流经格栅时,将在格栅板边沿发生衍射并形成衍射波,衍射波相互干扰导致能量衰减,从而达到减小反射波的目的。需要指出的是,吸波板自身对入射波也有一定反射作用,但相对较小,并且在后续波浪反射率的计算中可一并考虑。
吸波措施的吸波效果可由反射率KR评估[23]。需要指出的是,文献[23]中,反射率的评估基于试验波高,而本研究中由于模型箱空间限制未安装浪高仪对波高进行测量,因此,需基于海床表面实测波压力对反射率进行间接估算[18−20]。经检验,本文试验工况下,采用线性波理论与Stokes二阶波理论得到的波高与实测波压力反算得到的波高相对误差在3.4%以内,说明波高与波压力间的线性程度较好,采用波压力评估反射率与直接采用波高进行评估相比无显著误差,可以采用压力波间接估算反射率。
在泥面处,入射波和反射波的波压力方程分别为:

式中:uI和uR分别为入射波和反射波在泥面处的波压力;aR和aI分别为反射波和入射波在泥面处的波压力幅值;εI和εR分别为入射波和反射波的相位角;t为时间。
在相距Δl的两点x1和x2处(x2=x1+Δl),叠加波的波压力方程可通过傅里叶变换分别表示为:

式中:A1,B1,A2和B2为傅里叶系数,可根据实测的波压力时程曲线u1(t)和u2(t)得到。
联立式(4)~(7)可得入射波和反射波的波压力幅值分别为[23]:


从而可以根据KR=aR/aI得到反射率KR。
在正式试验前,通过离心模型预试验对吸波模块的吸波效果进行检验,试验具体参数如下:离心加速度为10g,模型水深为0.08 m,造波频率分别为1.0,2.0和2.5 Hz,由式(2)可以得到对应的模型波长分别为2.78,1.37和1.08 m。反射率KR与吸波距离(吸波板与较近一侧模型箱壁的距离)的关系如图4所示。从图4可以发现,当造波频率为2.5 Hz 时,吸波效果较好,且在吸波距离为0.20~0.25 m时,KR的最小值达到0.15。根据图中吸波距离及各频率对应的波长计算可知:当吸波距离与试验波长之比为0.18~0.23 时,KR较小,吸波效果较好。CHANEY 等[18]在相似的试验中也发现,在吸波距离与试验波浪波长之比为0.23 时KR达到最小,与本文预试验结果相似。而当造波频率为1.0 Hz时,其理论最佳吸波距离约为0.64 m,由于造波模型箱的尺寸限制,吸波距离无法达到最佳值,因此,吸波效果较差。这表明,在实际试验中,需依据波浪参数严格选择合适吸波距离,使得吸波距离与试验波长之比处于合理范围内(0.18~0.23),从而减小反射波对试验的影响。
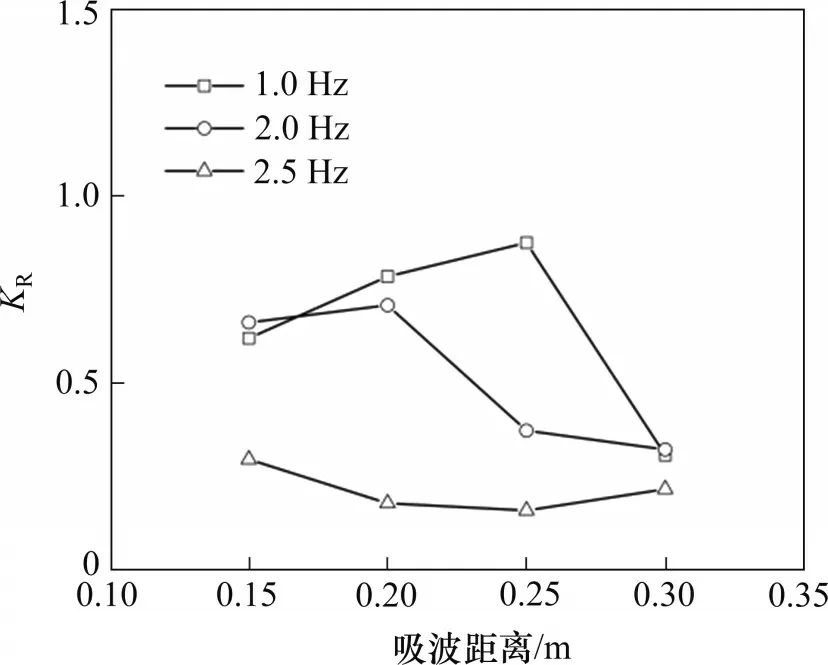
图4 吸波距离对反射率的影响Fig.4 Influence of distance between absorbing partition and side wall on reflection coefficient
2 造波离心模型试验
将改进后的机载装置搭载于浙江大学土工离心机ZJU-400上进行造波离心模型试验,该离心机有效旋转半径为4.5 m,最大离心加速度为150g。本试验采用的离心加速度为20g。
离心模型试验布置如图5所示,其中:孔压计1~6分别距泥面27,55,70,110,190和300 mm。模型海床长×宽×高为0.55 m×0.28 m×0.45 m,在制备软黏土模型海床前,将4根塑料排水管呈放射状布置在模型箱底部,然后在模型箱底铺设0.03 m厚的粗砂垫层,并在粗砂层上直接铺设一层土工布防止软黏土与粗砂层直接接触;通过模型箱底部的2个阀门缓慢地注入无气水,直至水面高于粗砂层表面以确保粗砂层饱和,饱和后将底部阀门关闭。采用马来西亚高岭土模型海床,其基本物理力学参数[24]为:相对密度Gs=2.60,液限wL=80%,塑限wP=35%,泊松比ν=0.33,渗透系数ks=2.0×10−8m/s,内摩擦角φ=23°,等向固结压缩系数λ=0.244,回弹系数κ=0.053,临界状态应力比M=0.9,临界孔隙比ecs=2.221。在制模过程中,首先,将马来西亚高岭土粉末与水以质量比1:1.6(2倍液限)混合,并通过负压搅拌4 h形成泥浆,然后,将泥浆轻柔地放入模型箱内,在转移过程中保持泥浆始终位于模型箱中水位以下,以保证最终模型海床的饱和度;再将装有泥浆的模型箱吊入离心机,在20g下固结40 h,得到试验模型海床。制得模型海床后,向模型箱内加水,使得水位高出泥面0.25 m,转机至20g后,在第一次波浪加载前保持转机2 h以上使海床内部超静孔压趋于平稳,此时,根据孔压计算得到海床固结度约为90%,根据制模完成后的质量和体积计算得到其饱和密度为1 594 kg/m³。
在海床表面及不同深度处埋置孔压计,并固定于特制支架上以免在试验过程中发生位移,记录波浪作用下海床内部孔压响应规律,孔压计布置见图5,以泥面为z轴原点O,向上为正。需要指出的是,为使得离心加速度为Ng条件下波浪作用及土体固结的时间相似率一致,在无黏性土造波离心模型试验中一般采用高黏度的硅油作为试验过程中的流体[10]。而对于软黏土,一方面,若孔隙流体采用硅油会改变软黏土颗粒与水之间的化学作用,无法反映饱和软黏土的真实特性;另一方面,软黏土渗透性较低,在短时间动力荷载作用下可认为海床地基内固结作用不明显[25]。因此,本试验采用水作为软黏土内部孔隙流体及外部流体,在波浪加载时,波浪作用为主导因素,模型时间为原型时间的1/N,而在间歇期内,土体固结占据主导,模型时间为原型时间的1/N2[16]。
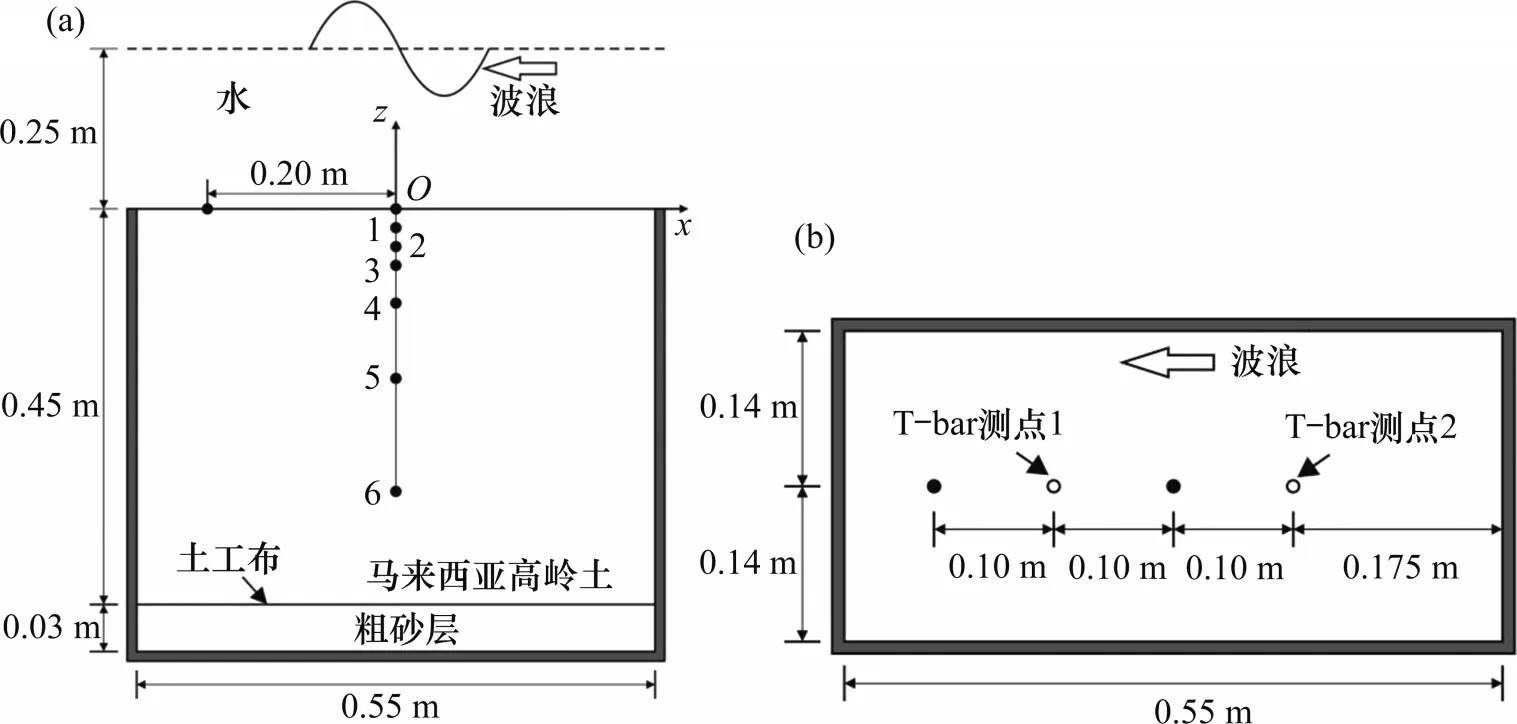
图5 离心模型试验布置Fig.5 Layout of centrifuge test
为了模拟水深5 m,周期分别为6 s 和5 s 的原型波浪,试验中设水深为0.25 m,造波频率分别为3.3 Hz和4.0 Hz,处于我国近海典型波浪周期范围内[26]。根据典型热带气旋所造成风浪的相应时间范围确定波浪持续时间和间隔时间[27],试验中一共进行3次波浪加载,其中,第一次和第二次加载过程为:3.3 Hz 波浪加载600 s(原型波浪加载200 min),停止造波,保持间歇期3 240 s(原型波浪间歇15 d)以使海床重固结;第三次加载过程为:4.0 Hz 波浪加载600 s,停止造波,保持间歇期3 240 s。观测波浪作用下软黏土海床内多次孔压上升和消散全过程。
3 试验结果
3.1 典型孔压时程曲线
图6所示为典型深度处孔压时程曲线。本试验中,连接轮盘直径为0.12 m,水深为0.25 m,由此可得划水距离为62 mm,结合式(1)~(3)计算得频率为3.3 Hz 和4.0 Hz 的波浪波长分别为1.90 m 和1.52 m,在泥面处形成的波压力幅值p0分别为2.14 kPa 和2.32 kPa,这与图6(a)中的实测值2.19 kPa 和2.31 kPa 基本一致。根据实测波压力幅值,由式(2)计算3.3 Hz 和4.0 Hz 的波浪波高为30.4 mm 和37.4 mm。需要说明的是,试验中所造波浪可能不是严格的线性波,因此,上述计算所得的波高与波长可能存在误差,但考虑到2种波浪工况的非线性程度较小,误差处于可接受范围内。根据2 种波浪工况的波长选定吸波距离为0.35 m,经计算反射率KR分别为0.19 和0.17,表明试验中吸波效果良好。从波压力波形的放大图可以进一步发现波浪为完整、稳定的正弦波。结果表明,所采用的机载波浪模拟实验装置具备良好、可控的造波和吸波能力,这为后续的试验提供了基础。
图6(b)~(d)所示为波浪作用下海床内部深度为27,55和70 mm处的孔压时程曲线。从图6(b)~(d)可以发现:在波浪作用下,海床内部超静孔隙水压力均有不同程度上升。许多研究将初始竖向有效应力作为超静孔隙水压力上升的极限值[10],因此,图中同时标出了相应深度处土体的初始竖向有效应力,其值由土体重度沿深度积分得到,土体重度沿深度的分布则根据马来西亚高岭土的临界状态孔隙比、压缩系数和回弹系数采用迭代方法确定[28]。需要指出的是,在第一次造波开始前,海床内部仍然存在较低超静孔隙水压力,因此,图中孔压时程曲线的起点并不为0。初始残余孔压的存在一定程度上影响了波浪加载初期海床响应,并加快了流态化现象的发生,但对海床流态化行为特性和流态化发生后的响应影响较小,同时,试验中初始残余孔压相对较小。初始超静孔压为孔压实际值与静水压力理论值之差,不同深度处的静水压力ps可根据下式计算:

图6 典型深度处孔压时程曲线Fig.6 Pore pressure and time curves at typical depths
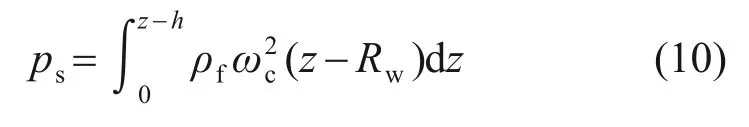
式中:ωc为离心机的角速度,设为6.94 rad/s;Rw为离心机转轴与水面距离,为3.67 m。
波浪引起的海床内部超静孔压ue通常可分解为残余孔压ures和振荡孔压uosc[10],前者主要由海床土体在循环剪切作用下的体变效应形成,例如当土体发生剪缩而由于渗透性较低,孔隙水无法在短时间内排出时,会引起残余孔压上升;而后者则反映了波浪荷载固有的周期特性。为了更好地对波浪作用下海床内部超静孔压的发展和消散规律进行研究,利用信号分析方法提取了孔压时程曲线中不同频率部分,从而将其分解为残余孔压和振荡孔压。图7所示为对70 mm深处第一次造波期间的孔压时程曲线进行分解得到的残余孔压和振荡孔压时程曲线。从图7可以发现:残余孔压不断累积,而振荡孔压部分则围绕着0 kPa 呈周期振荡。

图7 通过信号分析得到的残余孔压和振荡孔压Fig.7 Residual and oscillatory pore pressure obtained through signal analysis
3.2 残余孔压发展规律
后,残余孔压存在较大回升。该现象与TZANG等[29−31]的水槽造波试验结果类似。需要说明的是,实测孔压时程曲线(图6)中未发现上述现象,而残余孔压(图8)是基于实测孔压通过信号分析分离得到,这一处理过程中包含了人为假定误差,例如,假设振荡孔压分量围绕残余孔压呈对称分布。此外,通过观测试验录像也可发现残余孔压的发展与海床的流态化振荡现象有关,即孔压发展至接近有效应力水平后的突降时刻与海床流态化发生时刻高度吻合。这可能是因为[14,29]:1) 超静孔压

图8 海床不同深度残余孔压时程曲线Fig.8 Residual pore pressure and time curves of seabed at different depths
图8所示为海床不同深度处残余孔压时程曲线。从图8(a)可见,在第一次波浪作用开始之后,浅层海床内残余孔压迅速累积,在接近各自深度处相应的竖向有效应力时下降;在波浪加载停止的累积使得土体联结结构破坏,原本稳定的海床在受到波浪激励发生流态化运动的过程中存在向上部水体扩散的趋势,导致孔隙体积增大,孔压下降;2)表层海床在波浪作用下发生侵蚀,部分土颗粒悬扬至上部水体,因此降低了孔压计测点处上覆土质量,导致该处的最大孔压降低。当停止造波时,与残余孔压下降对应,流态化的海床停止运动,处于运动状态的海床土体重新开始沉积,此时,土体自重完全由孔隙水压力承担,因此,残余孔压突增;而波浪作用过程中悬扬至水体中的黏土颗粒由于沉降较慢,不是引起孔压回升的主要原因。
在后续的波浪加载中,残余孔压的响应与初次造波期间的类似,但残余孔压的最大值均有小幅下降,该现象可能是由于经过之前的波浪加载和重固结过程,土体颗粒重新排列变得更为密实,这一预剪作用一方面使海床在经受后续循环波浪荷载时超静孔压更难累积,另一方面导致海床发生沉降,由于各深度处的孔压计固定于支架,因此相当于减小了各孔压计的有效埋深,从而减小了相应位置的竖向有效应力。
从图8(b)可见:深度0.11,0.19 和0.30 m 处的残余孔压未达到相应的竖向有效应力,因此,未发生流态化运动的现象,其残余孔压发展在波浪加载期表现出与浅部海床不同的特性,即残余孔压将上升至极限值后进入平台段。而在后续波浪加载期间,与浅部海床类似,由于之前波浪荷载的预剪作用和重固结,残余孔压所达到的最大值较之前波浪加载期内小。
在间歇期内,海床内部超静孔隙水压力将逐渐消散。在本次试验中,在原型波浪的间歇期15 d内,由于黏性土渗透系数较小,累积残余孔压无法完成消散,例如深度0.07 m 处(对应原型波浪1.4 m深度)的残余孔压在经过第一次间歇期15 d后仍有5.3 kPa,达到初始竖向有效应力的78%,这将对该处海床的强度产生较大影响,且持续时间较长,这一现象需在实际工程中予以考虑。
3.3 振荡孔压发展规律
图9所示为波浪加载期间海床不同深度处振荡孔压时程曲线。从图9可以发现,浅部海床(深度70 mm 以内)的振荡孔压幅值变化较大,例如,深度为27 mm 处,振荡孔压幅值从第一次波浪加载50 s时的0.95p0发展为500 s时的0.40p0,呈现急剧衰减的规律,在后2次波浪加载中,其幅值虽较稳定,但仍然在0.70p0以下;而深度0.07 m 处,振荡孔压幅值从波浪加载50 s时的0.64p0发展为500 s时的1.07p0,在第2 次波浪加载期间,甚至超过了1.20p0。上述流态化海床内部振荡孔压幅值的显著变化在已有研究中也有涉及[32−33],并被认为是判断海床发生流态化的依据之一。相较而言,深部海床的振荡孔压幅值变化较小,且符合以往研究中沿深度逐渐衰减的规律。
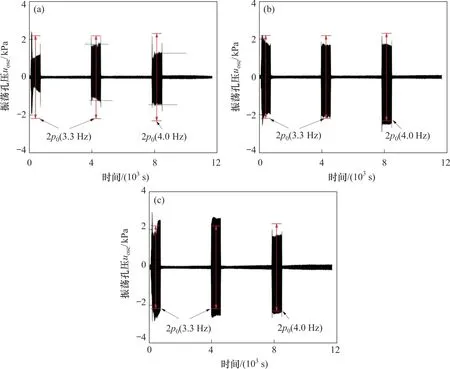
图9 海床不同深度处振荡孔压时程曲线Fig.9 Oscillatory pore pressure and time curves of of seabed at different depths
TZANG 等[29]指出,波浪作用下海床的动力响应与海床表层的边界层厚度δ相关,在边界层内,孔压幅值急剧衰减,δ的表达式为
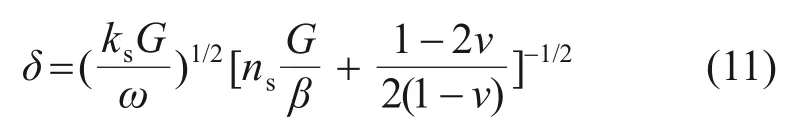
式中:G为土体剪切模量;ns为土体孔隙率;β为流体的体积模量。
取G=1×106Pa,ns=0.67,β=2×109Pa,则频率3.3 Hz 和4.0 Hz 的波浪对应边界层厚度分别为62 mm 和56 mm,这在一定程度上解释了深度27 mm 处孔压幅值的衰减情况。另外,在深度70 mm 处,孔压幅值超过了泥面处波压力幅值p0。SASSA 等[10]针对砂土海床的离心造波模型试验以及FODA 等[30]针对粉土海床的常重力水槽造波试验中也有类似现象。因此,可以认为海床一定深度处孔压幅值的放大效应与波浪作用下海床的液化或流态化密切相关。FODA等[30]认为,上述现象由波浪作用下土体内部渗流通道形成,从而使得海床内部存在独立的波浪模式,引发了海床内部的共振效应,使得振荡孔压幅值增大,这一解释需要在试验过程中对海床内部微观结构进行进一步观测加以验证。
3.4 海床位移情况
试验中通过视频录像的方式观测到波浪加载期间海床内部超静孔压达到或接近初始竖向有效应力时,海床表层呈现流态化特性,随波浪发生振荡运动。在3次波浪加载期间,海床表面振荡幅值均为3 mm 左右(对应原型波浪振荡幅值为60 mm)。SASSA 等[34]采用双层流体运动理论,将海水和流态化海床考虑为不同密度的理想流体,给出了波浪作用下海床表面振荡幅值a0的计算表达式:

式中:ρf为海水密度,取1 000 kg/m3;ρs为流态化海床密度,取海床土体饱和密度1 594 kg/m3;zL为流态化海床底部高程坐标,根据孔压和试验录像取为−70 mm;kL为双层流体的波数,其计算方法可参考文献[34]。
由式(12)可得频率为3.3 Hz 和4.0 Hz 的波浪作用下a0分别为2.3 mm和2.7 mm,与试验观测值(约3 mm)较为吻合。需要指出的是,式(12)的推导过程中存在诸如理想流体的简化且基于一维分析,但是对比文献[34]与离心模型试验结果可知,该式可以在一定程度上预测海床表面的振荡幅值,且所需参数较易确定,因此,本文采用该式计算振荡幅值a0。
图10所示为试验过程中海床表面沉降变化。从图10可以发现:在波浪加载期之后海床沉降较为明显,表明海床内部软黏土在循环波浪作用下剪缩效应占据主导,这也是海床内部超静孔压累积的主要原因。而在间歇期,海床内部的孔隙水不断排出,超静孔压逐渐消散,海床也因此发生一定程度的沉降,但相较于波浪加载期沉降量较小。试验结束时,海床表面最终沉降约13 mm。

图10 海床表面沉降Fig.10 Settlement of seabed surface
3.5 海床强度变化
在试验开始前和结束后对模型海床进行了3次T-bar 贯入试验以获取其不排水抗剪强度沿深度的分布,其中初始值测试点为测点1,试验结束后的测试点包含测点1 和测点2(如图5所示),T-bar 测试的结果如图11所示,其中,在T-bar贯入阻力与土体不排水抗剪强度换算过程中,承载力系数取10.5,试验后不排水抗剪强度结果是在所有造波试验完成之后,经过约20 min 的装置准备时间,通过T-bar 贯入试验测得,此时,波致超静孔压已大幅消散(如图8所示)。由图11可以发现:在试验开始前,海床内深度为0.04~0.10 m的土体强度较低,而经历多次波浪循环加载−重固结过程后,该处土体形成了一层强度突增的“夹层”,这一夹层范围与波浪加载过程中海床发生流态化运动的区域十分吻合,这可能是由于该处土体联结结构破坏及重排列更为彻底,在重固结过程中所形成的土体结构更为紧密,因此强度更高,海床表面观测到的沉降(如图10所示)也支持了上述致密化的推断。而较深海床处并未达到流态化,波浪预剪和重固结作用虽然也使得其发生了一定的致密化,强度有所提升,但幅度较小。上述波浪作用−重固结循环后海床发生致密化现象与MIYAMOTO等[35]在针对砂土海床的离心造波模型试验中和WANG 等[36]对波浪作用下黄河三角洲区域海床地基的原位观测中所观测到的现象吻合。

图11 T-bar测试结果Fig.11 Results of T-bar test
需要指出的是:由于臂式离心机吊篮尺寸限制,本文试验中模型箱长度小于试验波长,因此,本文与以往臂式离心机中开展的造波试验有类似的局限性[10]。在试验波长与模型箱尺寸控制方面,鼓式离心机[19−20]和常重力水槽[8−9]中开展的造波试验有一定优势。但总体而言,本试验中海床表面波压力幅值较大,波形较好,且呈现周期性振荡的基本规律,所观测到的海床响应规律与模型箱尺寸超过波长的造波试验结果[29−31]相比一致性较好,因此试验结果仍具有一定普适性。今后,需进行更大尺度造波模型箱和更高性能造波实验装置的研制。此外,试验中较难观测的海床应力应变响应等规律亦依赖可靠的数值模型加以刻画[32−33]。
4 结论
1)通过海床表面波压力数据验证了离心机机载造波实验装置模拟海洋波浪作用的有效性,该装置为研究现场尺度波浪作用下海床及结构物动力响应问题提供了有效支撑。
2)当波浪作用导致海床内超静孔压累积至接近土体初始竖向有效应力时,海床发生流态化现象,其流态化深度可达1.4 m。超静孔压在原型波浪15 d 的间歇期内无法完成消散,表明其将对海床产生长期影响。
3)呈现流态化的海床内部振荡孔压幅值变化十分剧烈,在边界层内孔压振荡幅值衰减明显,而在接近流态化区域底部,孔压幅值可能超过海床表面处波压力幅值。
4)多次波浪荷载和间歇期内的孔压累积−消散循环将导致海床发生致密化,显著提升海床抵抗波致超静孔压累积的能力;由于海床浅部致密化效应最为显著,可能导致强度突增夹层的产生。
