新型螺旋槽干气密封流固耦合分析*

2022-09-21张伟政赵吉军张献中张琦璇

润滑与密封 2022年9期

张伟政赵吉军张献中张琦璇

(兰州理工大学石油化工学院甘肃兰州 730050)

干气密封作为密封装置的典型代表被应用在诸多领域，其具有泄漏量低、损耗小、可靠性高等优点[1]。与传统机械密封相比，干气密封动、静环之间非接触，且根据实际需要在动环上雕刻出不同形状的沟槽或织构用以增强其动压效应，常见的槽型有螺旋槽、T形槽和圆形槽等。干气密封在运行过程中，动环跟随轴体转动，且其上面的微米级浅槽分布具有一定的规律性和周期性。当密封气体进入密封间隙后，因其黏度较小而压力较大，使两密封端面分开，同时会在密封端面间形成微米级气膜，实现非接触式密封[1]；另外气膜有效地防止了密封介质的泄漏，同时又在隔热与润滑方面起到了重要的作用。近年来，随着社会的发展与科技的进步，工业生产对密封技术的要求不断提高，国内外学者也对此进行了更为深入的研究[2]。针对螺旋槽干气密封的研究，多采用有限元数值模拟[2]与实验的方法。通过对其流场与流固耦合的分析，可以研究固体形变与流体之间的相互作用影响，从而指导干气密封槽型的设计与优化。随着ANSYS软件的不断发展与完善，流固耦合的计算与研究也取得了很大的进步，并且流固耦合在工程领域的应用也逐渐广泛起来。流固耦合的研究计算不但能节约大量的时间，还能够更加贴近真实工况。早在20世纪80年代，ETSION[3-4]就对机械密封展开研究，为后续干气密封的研究做好了充足的准备；SEDY[5]首次陈述了提升干气密封性能的方法；BONNEAU等[6]对槽型气体推力轴承及槽型气体密封进行了有限元分析；TOUMERIE等[7]探究了螺旋槽几何机构对其密封性能的影响；文献[8-10]对螺旋槽干气密封的流场进行了分析。2010年，丁雪兴课题组利用Fluent流体计算软件，针对不同膜厚的螺旋槽干气密封流场进行模拟计算，得到流场压力分布情况，并对螺旋槽干气密封的槽深与螺旋角2个几何参数提出了优化方案[11-14]。邓成香[15]基于ANSYS Workbench软件对螺旋槽干气密封流固耦合进行了计算研究。2017年，陈洋洋等[16-17]利用ANSYS软件，对螺旋槽干气密封进行了双向流固耦合计算，并讨论了在不同结构参数下螺旋槽干气密封在双向流固耦合下的密封环应力应变情况。2018年，陈文奇等[18]对双螺旋角槽干气密封的槽型进行了优化设计。2020年，左松奇等[19]对一种新型组合槽型的密封特性进行了研究。

通过对传统螺旋槽的流场进行数值模拟可知，在其背风口处有一处明显的低压区，这是由于在螺旋槽的背面产生了一定程度上的气体分离，为提高传统螺旋槽的密封性能，本文作者提出一种新型螺旋槽结构,利用ANSYS等相关软件建立了新型螺旋槽与传统螺旋槽的密封环模型，在相同工况条件下对其进行了受力分析及选材后对两槽型密封端面进行流固耦合计算，比较分析了2种槽型密封环的应力、变形差异。

1 新型螺旋槽密封端面结构

为提高传统螺旋槽的密封性能，对其结构进行了优化。在传统螺旋槽的背风口处，并列了一个相对较短螺旋槽，且2个并列螺旋槽的槽深相等，使其成为一个长螺旋槽，两槽的槽深均为微米级别。建立的新型螺旋槽的结构如图1所示。

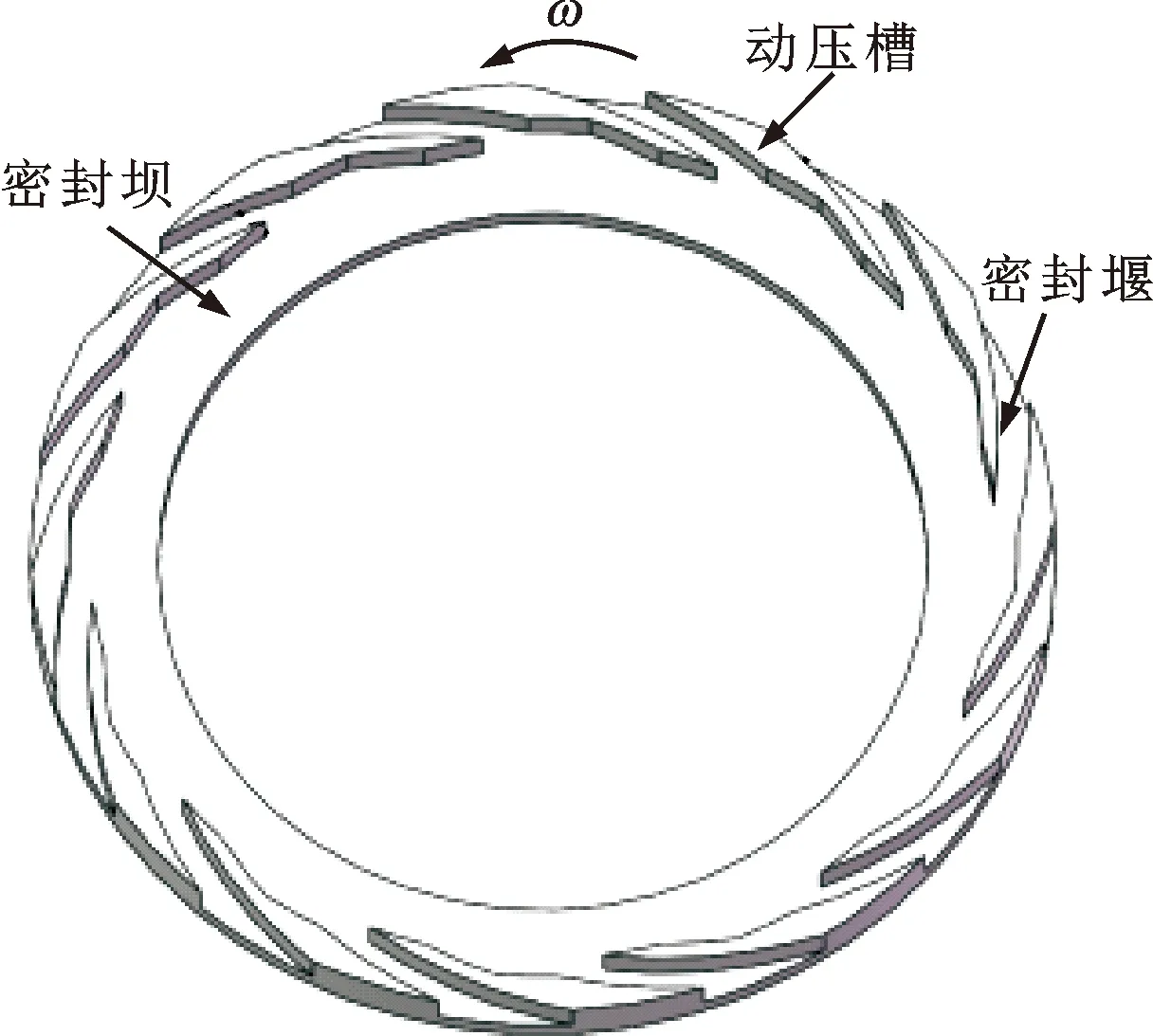
图1 新型螺旋槽干气密封动环结构

2 流固耦合基本方程

2.1 流体控制方程

流体在流场中的流动遵循基本的物理学定义(质量守恒定律、能量守恒定律、动量守恒定律)。

(1)连续性方程

质量守恒方程就是连续性方程，所有流体在流场中流动均要遵循质量守恒定律，该方程的微分形式为

(1)

式中:ux、uy、uz分别表示在坐标轴3个方向上的分量，m/s;t为时间;ρ为密度。

引入哈密顿算子：

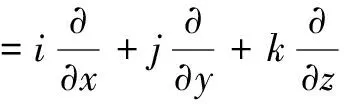
(2)

则可将式(1)表示为

(3)

连续性方程在圆柱坐标系中可表示为

(4)

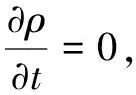
(5)

当流体为不可压缩流体时，有：

(6)

在圆柱坐标下的表示形式为

(7)

(2)动量守恒方程

动量守恒方程遵循牛顿第二定律，根据牛顿第二定律，可得x、y、z方向上的动量方程为

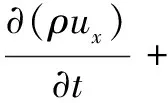
(8)

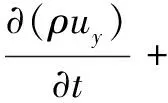
(9)

(10)

式中：p为流体中微团体上的压力，Pa；τxx、τxy、τxz指分子在黏性的作用下在微单元表面上产生的应力τ的分量，Pa；fx、fy、fz分别表示x、y、z方向上的质量力，m/s2。

(3)能量守恒方程

根据能量守恒定律，进入微单元热流量与质量力和表面力对其所作的功等于微单元内能量的增加量。表达式为

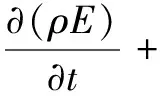
(11)

式中:E为微单元的总能量，J/kg，总能量包括内能、动能以及势能，表示为

(12)

h为焓，J/kg；hj为组分j的焓，J/kg；keff表示其有效热的传导系数，W/(m·K)；Jj为组分j的扩散通量；Sh表示了化学反应中的热。

2.2 固体控制方程

由于流场的作用引起固体的振动或位移，即固体的控制方程为

(13)

式中:Ms为质量矩阵；Cs为阻尼矩阵；Ks为刚度矩阵；ds为固体的位移，mm;τs为固体所受应力，MPa。

2.3 耦合控制方程

在分析计算流固耦合问题时，耦合交界面的固体与流体同样需满足相关的物理学守恒定律：

τf·nf=τs·ns

(14)

df=ds

(15)

式中：τf与τs分别对应的是流体应力和固体应力，MPa；df与ds分别对应的是流体位移与固体位移，mm。

3 密封环模型建立及网格划分

3.1 密封环模型的建立

密封环在不同的操作环境(压力、转速)下运行，由于流场的作用，导致密封环在运行过程中，其端面会有不同程度的形变，这将对干气密封的性能以及寿命产生极大影响。由于干气密封的密封环具有自我调节和恢复功能，只要作用力达到平衡，它就可以恢复到一个新的平衡操作间隙。由此可见，密封环之间的平行对于减少环之间的接触非常重要。

如图2所示，文中利用SolidWorks建模软件针对干气密封密封动环建立几何模型。

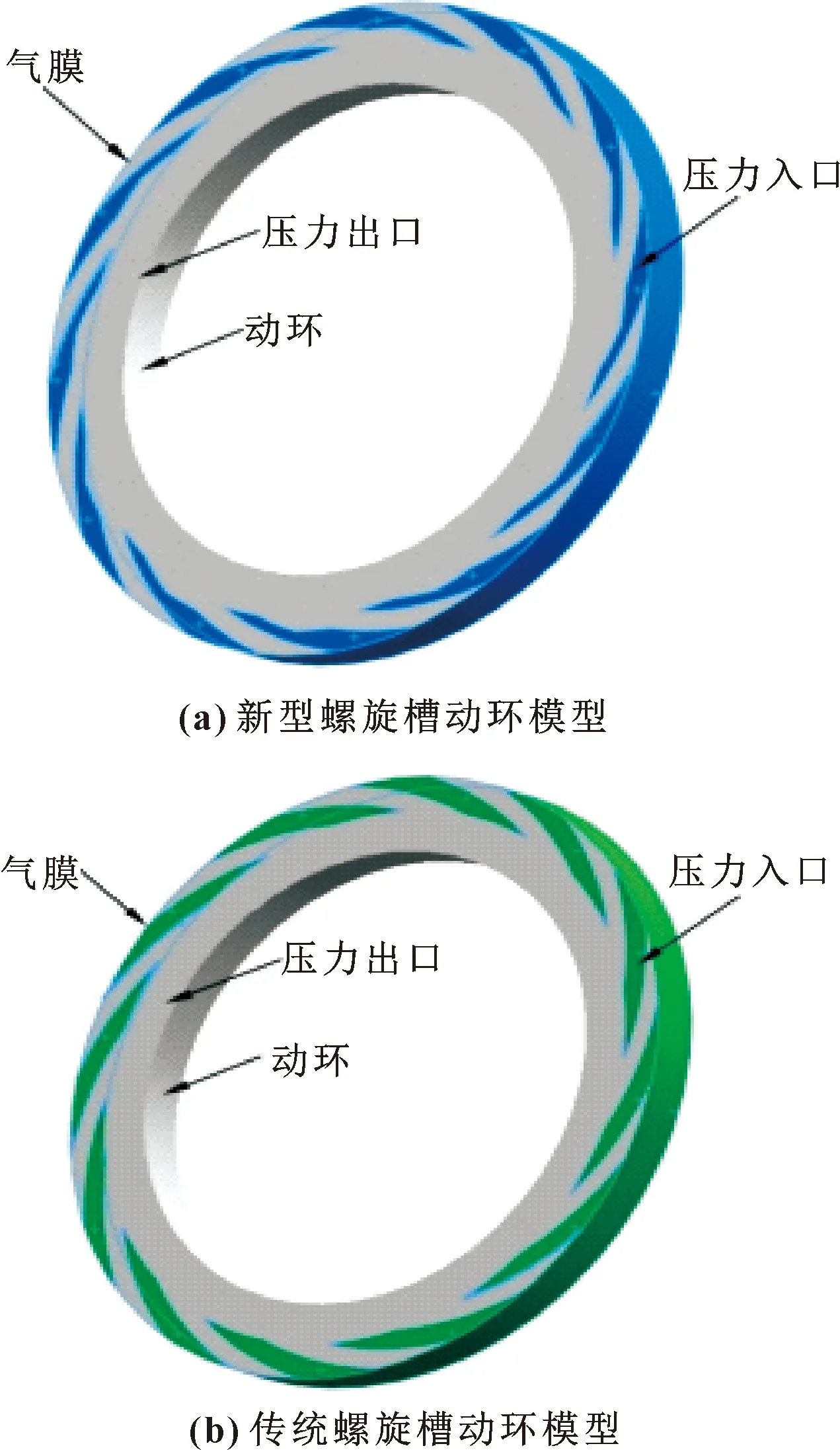
图2 2种槽型动环模型

3.2 密封环的网格划分

通常情况下，干气密封的密封槽是刻在动环上的，利用SolidWorks建模软件对新型螺旋槽干气密封建立三维模型。因为干气密封气膜成圆周形分布，且结构是中心对称结构，为了减少计算机的计算量，故而取整个气膜模型的1/Ng作为计算区域(Ng为密封端面新型螺旋槽的个数)。图3所示为所建立的新型螺旋槽气膜模型。螺旋槽气膜均是微米级的，文中为了方便观察，将其轴向放大1 000倍。

图3 新型螺旋槽1/12端面结构

将SolidWorks建模软件建好的模型导入ICEM中进行网格划分，干气密封端面气膜半径尺寸为毫米级别，而其气膜厚度与开槽深度均为微米级别，两者存在数量级差异。在网格划分过程中，这种跨尺度的网格划分是数值模拟中的一个难点。在ICEM中对干气密封气膜沿轴向放大1 000倍后进行网格划分，在导入Fluent软件进行计算时，用Scale模块再将划分好的网格沿轴向缩小1 000倍即可解决跨尺度划分网格的问题。

采用增加网格密度与沿厚度方向网格的方法来验证网格独立性。网格数量设置的合理对于模拟计算的精度及计算速度至关重要。以螺旋槽干气密封气膜厚度3 μm、槽深5 μm、槽数12、螺旋角15°、内径58.42 mm、外径77.78 mm、槽根半径9 mm、转速10 000 r/min、入口压力1 MPa、出口压力0.1 MPa为例，选取网格数量为5万～30万进行计算。网格数量对开启力变化的影响如图4所示，当网格数量达到135 640的时候，其开启力数值趋于稳定。据此认为：当网格数量达到135 640的时候满足网格无关性。新型螺旋槽的网格无关性检验与此相同。

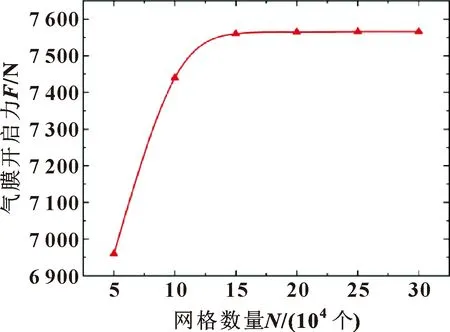
图4 网格无关性验证

3.3 边界条件的设置

新型螺旋槽1/Ng气膜边界条件的设置如图5所示。由于干气密封的流场结构是中心对称的，每个计算区域的流动具有相同性，则压力周期性边界条件为：p(θ+2π/12)=p(θ)，在ICEM中对计算区域进行划分并定义part和设置周期性边界条件，其中A1、A2、B1、B2为圆周的周期性边界。Top surface 为新型螺旋槽的旋转壁面，Bottom surface为新型螺旋槽的静止壁面，Pressure-inlet为新型螺旋槽的压力入口，Pressure-outlet为其压力出口。采用单旋转实现干气密封的动、静环之间的相对运动。且动、静环采用温降边界条件，其旋转速度为10 000～30 000 r/min，密封介质采用空气。

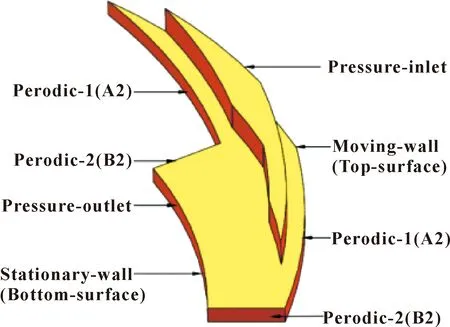
图5 新型螺旋槽边界条件示意

3.4 求解方法

将ICEM中划分好网格的模型导入Fluent中进行流体域求解，选择Laminar(层流模型)，并调用能量方程，算法采用SIMPLEC，密封介质为空气，选用理想气体模型。对扩散项采用中心差分法进行离散，对压力插值采用二阶迎风格式。将迭代精度设为1×10-5。将能量方程的迭代精度设为1×10-6。

4 密封环的受力分析与材料选择

4.1 流体进入干气密封环模型

在计算干气密封流固耦合流场时，流体分别按照速度与压力2种方式流入流场。按速度方式进入：表示为在动环的流体入口处设置关于速度的边界条件；按压力进入：是在动环的流体入口处设置关于压力的边界条件。如图6所示，为流体进入螺旋槽干气密封动环时压力边界条件与动静环的结构示意图。

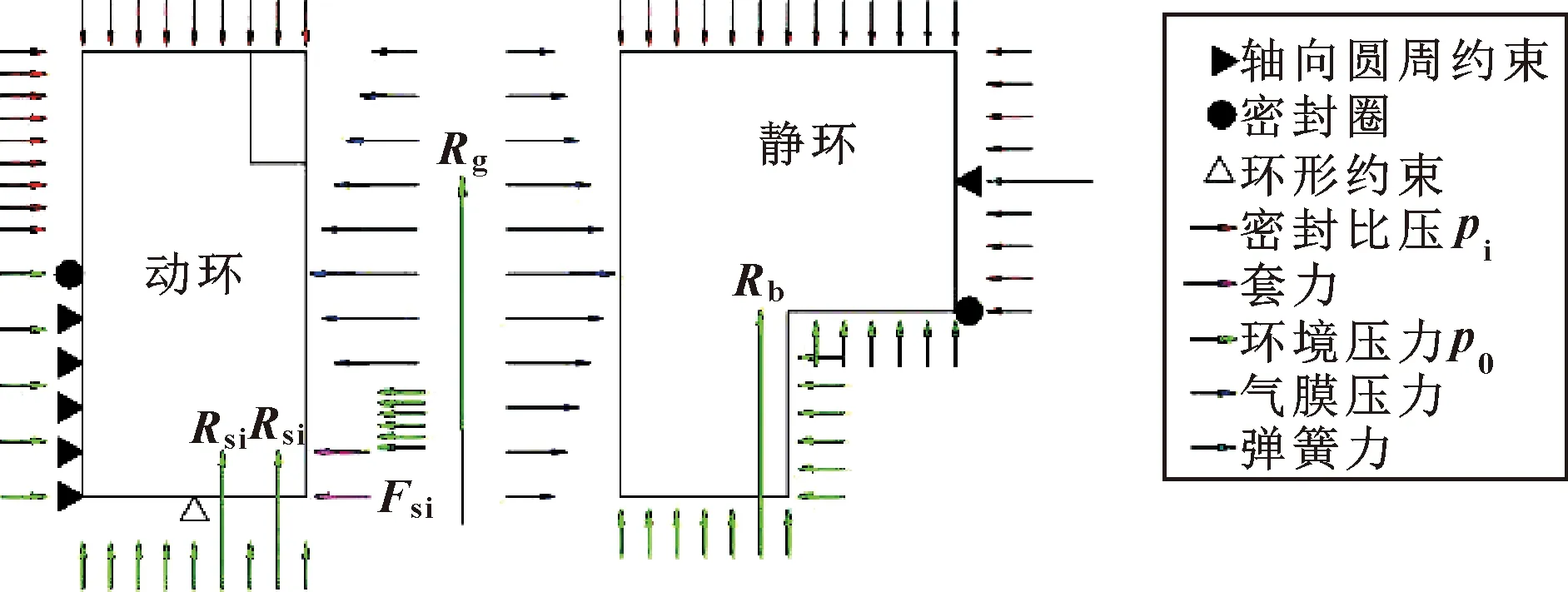
图6 流体进入螺旋槽动静环示意

4.2 干气密封密封环的受力分布

当干气密封启动且达到稳定时，动静环之间的受力需达到平衡。密封环之间的受力平衡是干气密封稳定运行的重要前提与保证。如图7所示，为干气密封密封环的受力模型。

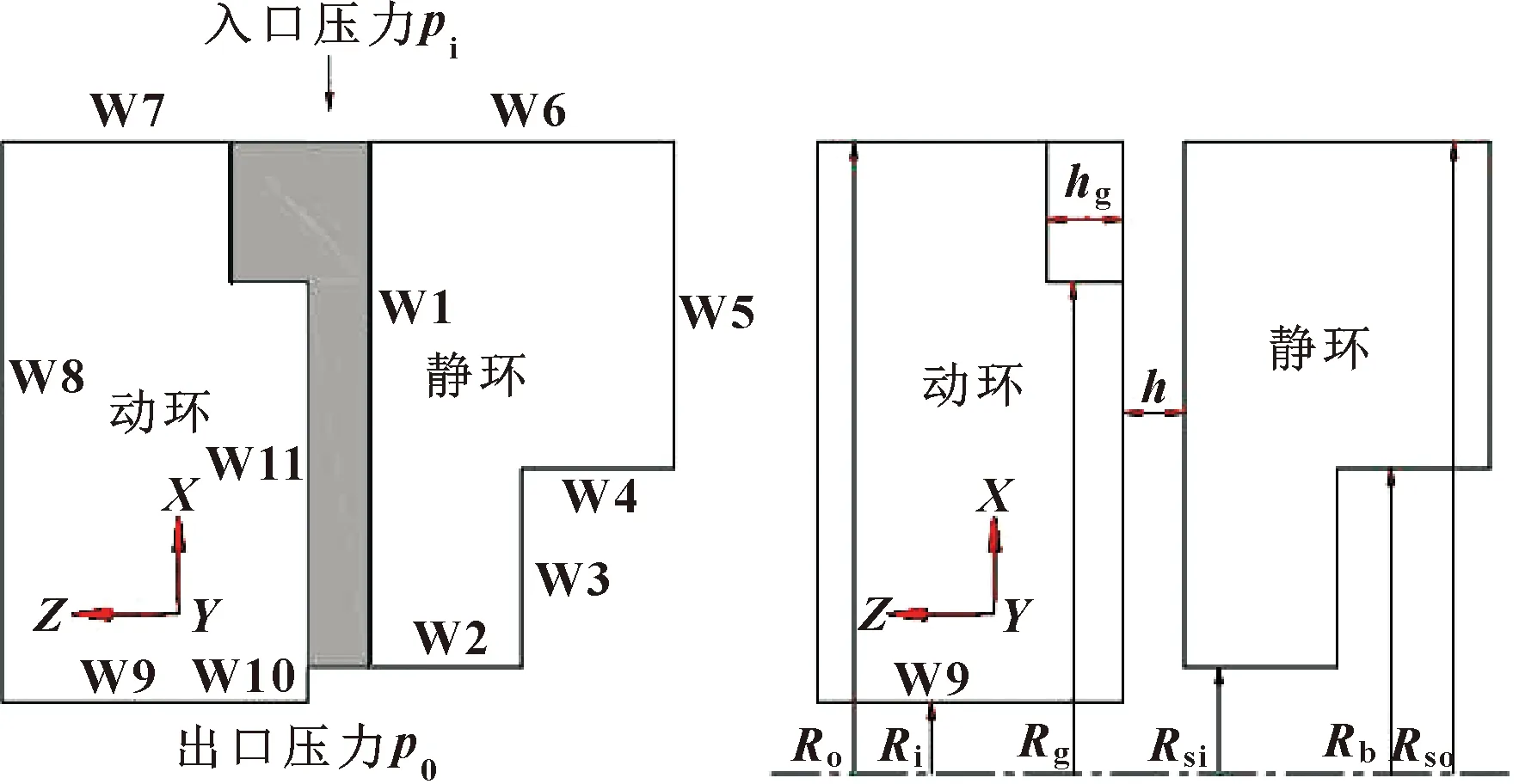
图7 动静环受力示意

4.3 密封环材料选择与受力后可能发生形变的位置

当干气密封在极端的工况下运行时，密封环由于摩擦碰撞或者受力不均等原因会发生不同程度上的变形，密封环发生形变的程度与其材料的选择和各个地方受到的载荷均有关系。文中选用碳化钨(WC)作为干气密封动静环的材料来研究螺旋槽干气密封与新型螺旋槽干气密封的密封环在工作中的应力应变情况。图8与图9所示分别为干气密封动、静环可能发生形变的位置。

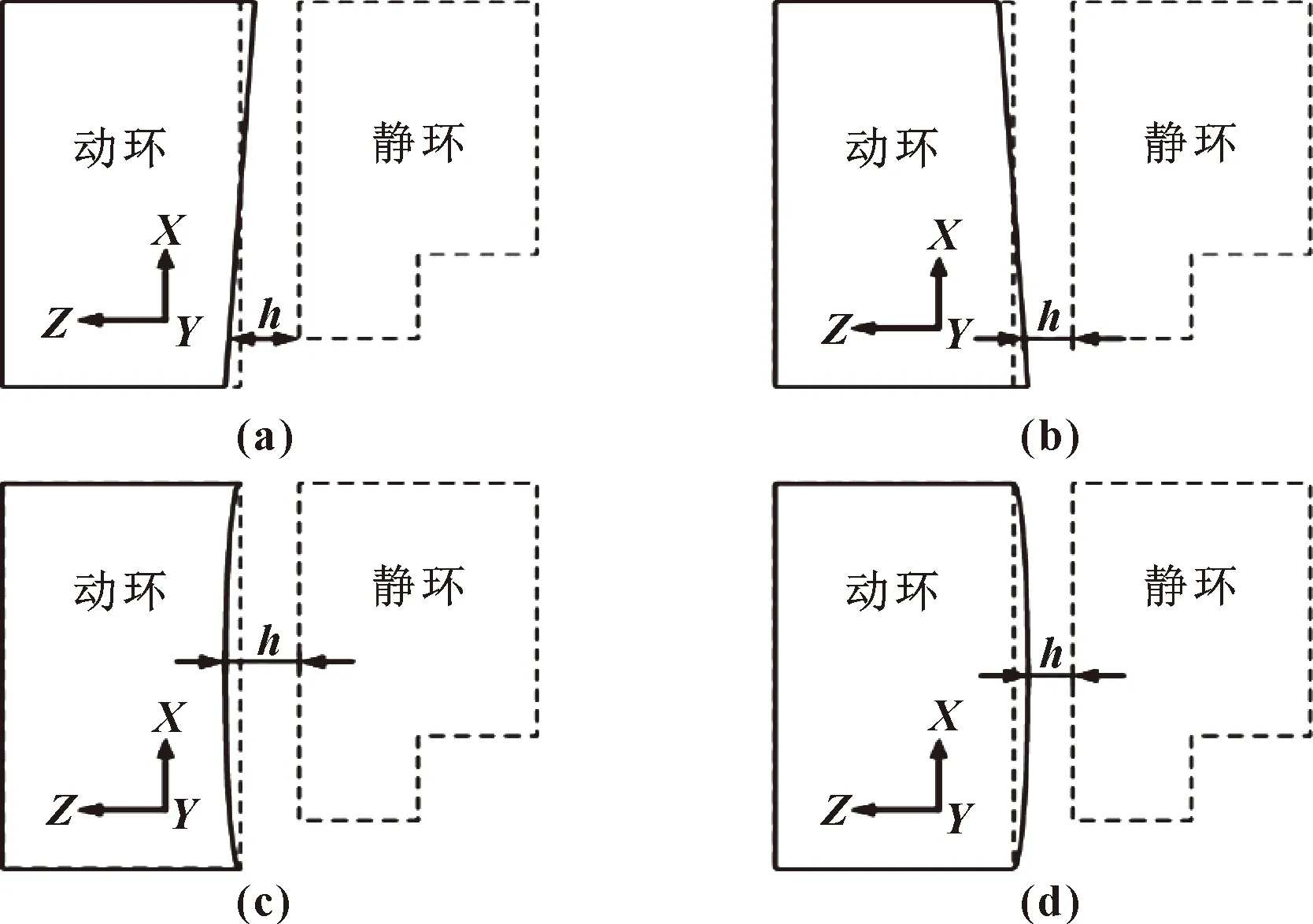
图8 动环发生形变的4种位置

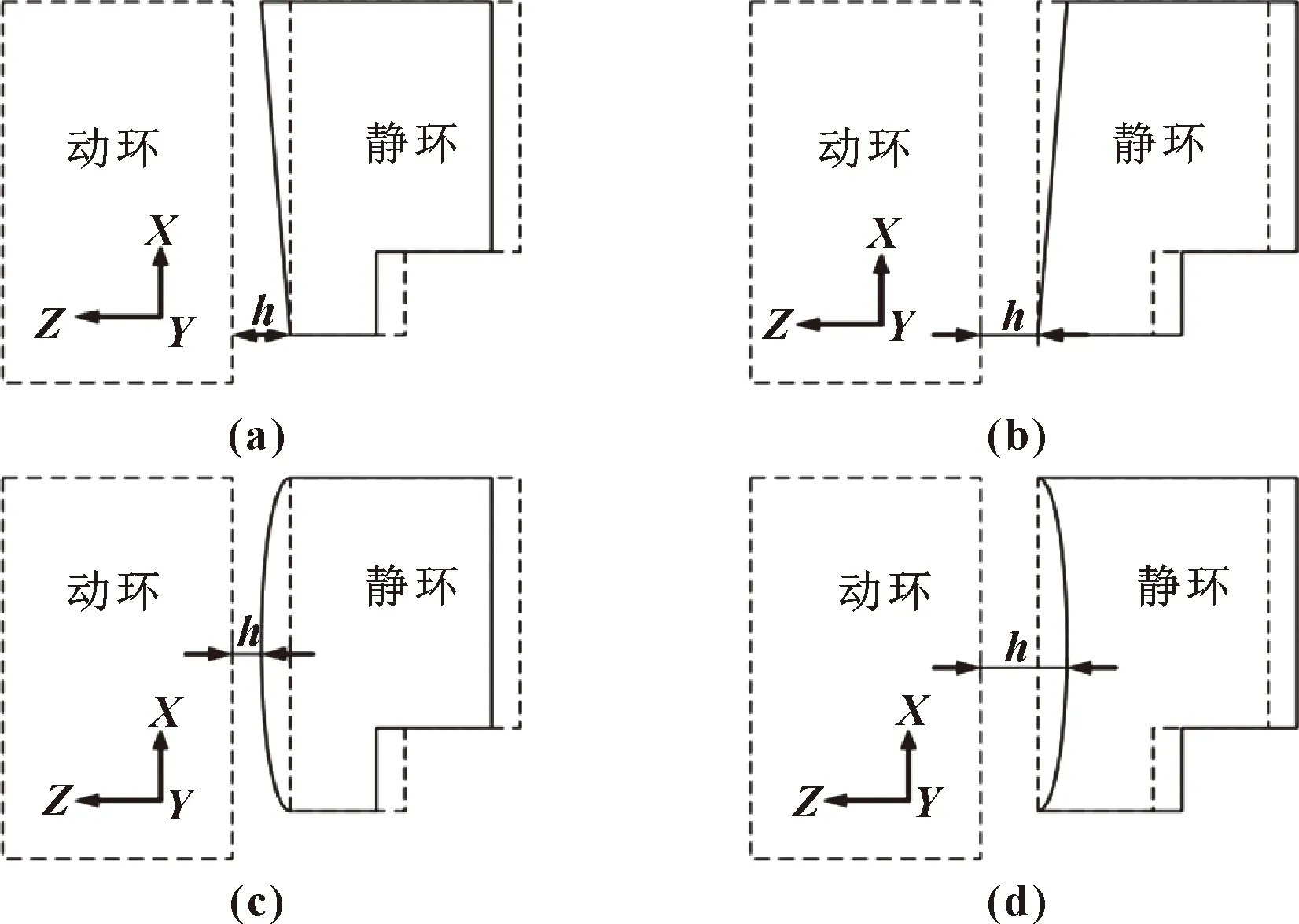
图9 静环可能发生形变的4种位置

在极端工况下干气密封运转时，密封环材料选择“硬碰硬”的密封模式会使其具有更良好的稳定性。故选取干气密封动静环材料均为碳化钨(WC)，其材料的物理参数如表1所示。

表1 2种干气密封槽型密封环材料参数

5 干气密封流固耦合过程

由于干气密封的结构相对简单，使用单向流固耦合计算足以对密封环在运转过程中发生的形变进行计算。文中在Workbench平台对其进行计算分析时，首先调入Fluid flow(Fluent)流场分析计算模块与Static-Structural结构场分析计算模块。并在Fluid flow(Fluent)模块中导入之前计算好的date & case(流场计算数据)文件。之后将流场模块与结构场模块进行耦合。将Fluid flow模块中的Solution选项拖动至Static-Structural模块中的set up选项当中。以上操作就完成了干气密封单向流固耦合的信息传导。然后将干气密封密封环模型保存为X-T格式并导入至Static-Structural模块中的Geometry当中，并在model中对干气密封的动静环进行网格划分。并按照实际工况对干气密封的动静环施加相应的约束条件与载荷。之后再在Solve中对其进行求解计算。图10与图11分别表示为干气密封流固耦合信息传导过程与干气密封密封环流场压力加载示意图。

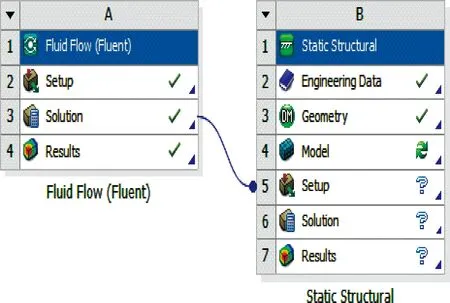
图10 流固耦合信息传导过程示意

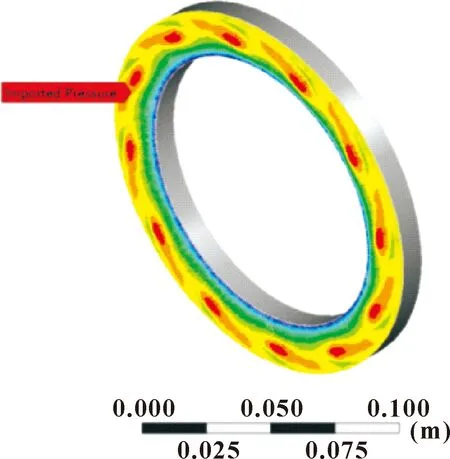
图11 密封环流场压力加载示意

5.1 流固耦合下密封环应力分析

在流场的计算中，取入口压力为1 MPa、出口压力为0.1 MPa、转速为10 000 r/min、入口温度为303.15 K、气膜厚度为3 μm、槽数为12、螺旋角为15°的螺旋槽干气密封所形成的气膜压力对密封环的影响进行计算。

5.1.1 干气密封动环流固耦合应力分析

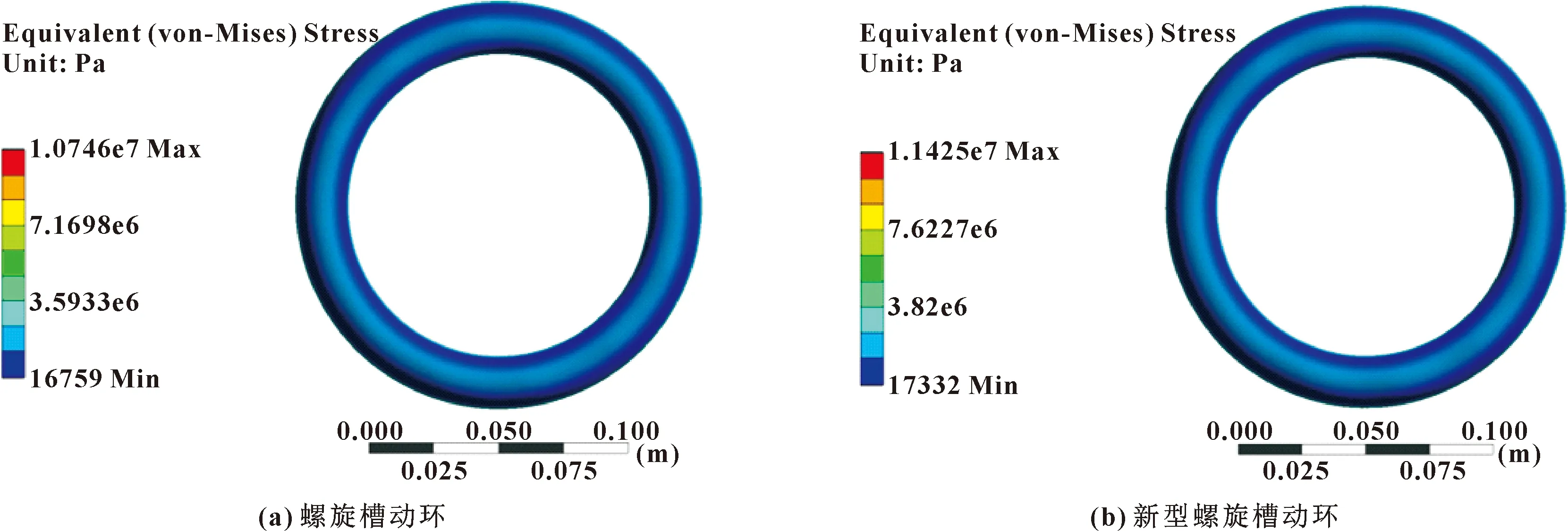
图12 2种槽型动环应力分布

5.1.2 干气密封静环流固耦合应力分析

在干气密封运行过程中，静环是始终保持静止不动的。在分析其流固耦合的过程中，静环不会因为旋转而产生更多的应力，静环只受流场耦合时对其产生的作用与影响。如图13所示。

由图13可知，当2种槽型的材料与工况相同时，新型螺旋槽的整体静环应力值要大于传统螺旋槽静环的应力值；传统螺旋槽干气密封的静环轴向气膜所产生的最大应力约为1.18 MPa,新型螺旋槽干气密封静环轴向气膜所产生的最大应力约为1.28 MPa。这是因为新型螺旋槽的气膜所产生的气膜力在静环表面上分布相比传统螺旋槽较大，使得在单位面积内静环所受到的压力也较大，故导致新型螺旋槽静环应力比传统螺旋槽静环应力大。

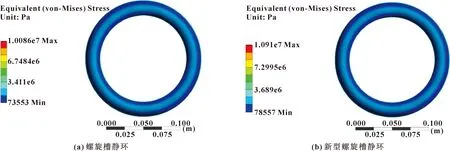
图13 2种槽型静环应力分布

5.1.3 转速对干气密封环流固耦合应力的影响

图14所示为在不同转速下新型螺旋槽与传统螺旋槽的动静环应力分布。

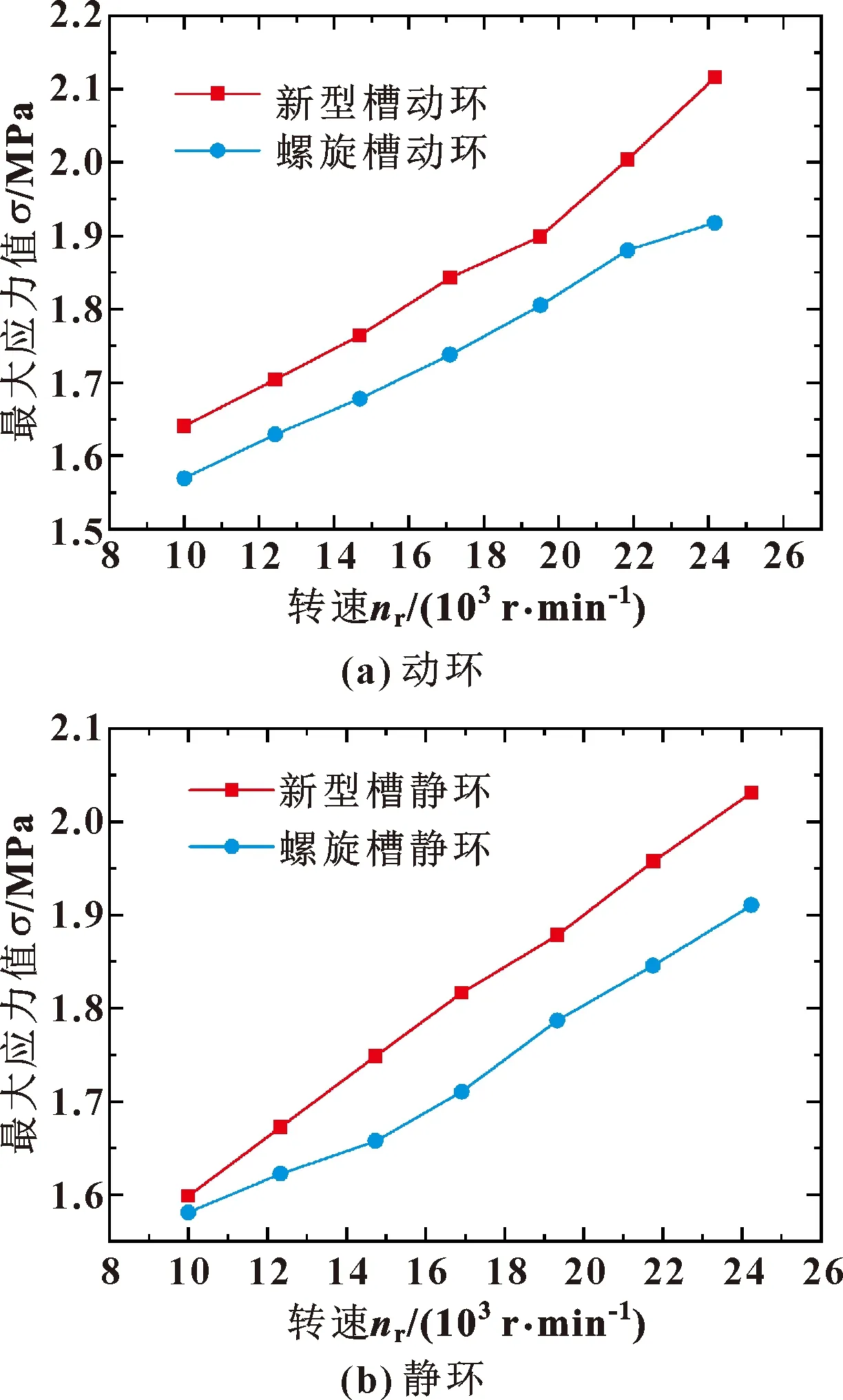
图14 转速对2种槽型动静环最大应力的影响

由图14可知，干气密封动、静环所产生的应力值随着转速的增大而增大，且新型螺旋槽的动静环应力值始终大于传统螺旋槽动静环应力值。随着转速的不断增加，两槽型压力差值也在不断变化，当转速在10 000 r/min时，两者动环应力差为0.07 MPa，当转速达到25 000 r/min时，两者动环应力差值为0.2 MPa；导致两者存在差异的原因可能有：(1)随着转速的增加，干气密封的涡动与离心效应得到了增强；(2)由于新型螺旋槽槽型的原因，使得其应力集中现象更加明显，导致新型螺旋槽的应力始终大于传统螺旋槽。新型螺旋槽的静环虽然为静止不动的部件，但是由于动环旋转所产生的气膜压力，最大气膜压力与最大应力呈拟线性关系，故使得新型螺旋槽静环表面的应力也始终大于传统螺旋槽静环。

5.1.4 入口压力对干气密封环流固耦合应力的影响

图15所示为在不同入口压力下新型螺旋槽与传统螺旋槽的动静环应力分布。可知，随着入口压力的增大，2种槽型的动、静环应力值均增大。当入口压力为1.25 MPa,出口压力为0.1 MPa时，传统螺旋槽动环的表面应力为1.45 MPa，静环的表面应力为1.39 MPa;新型螺旋槽动环的表面应力为1.54 MPa，静环的表面应力为1.5 MPa。当出口压力保持不变，入口压力增大至2.75 MPa时，传统螺旋槽动环表面应力为2.85 MPa，静环表面应力为2.61 MPa;新型螺旋槽动环的表面应力为3 MPa，静环的表面应力为2.74 MPa。与转速影响趋势相似，随着入口压力的增加，2种槽型的动、静环表面应力均增大，且新型螺旋槽的应力始终大于传统螺旋槽，并且动环上的应力始终大于静环，这是由于干气密封在运转时，动环高速旋转，产生了更多的盈余应力。

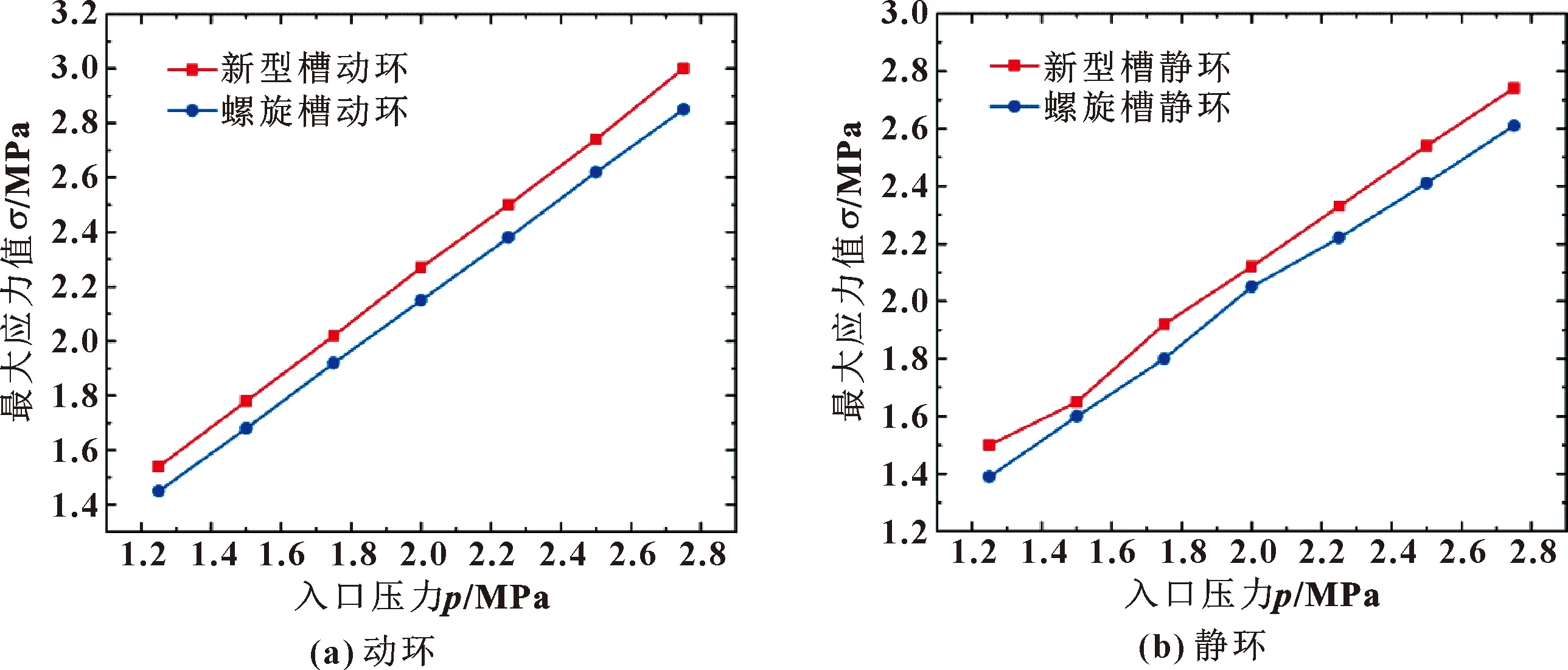
图15 入口压力对2种槽型动静环最大应力的影响

5.2 流固耦合下干气密封变形分析

在干气密封的流场分析中，仍取入口压力为1 MPa，出口压力为0.1 MPa，转速设为10 000 r/min，入口温度为303.15 K，螺旋槽槽数为12，螺旋角为15°，气膜厚度为3 μm，槽深为5 μm，来探究流固耦合下干气密封环变形情况。

5.2.1 干气密封动环流固耦合变形分析

图16所示为干气密封动环流固耦合变形分布。

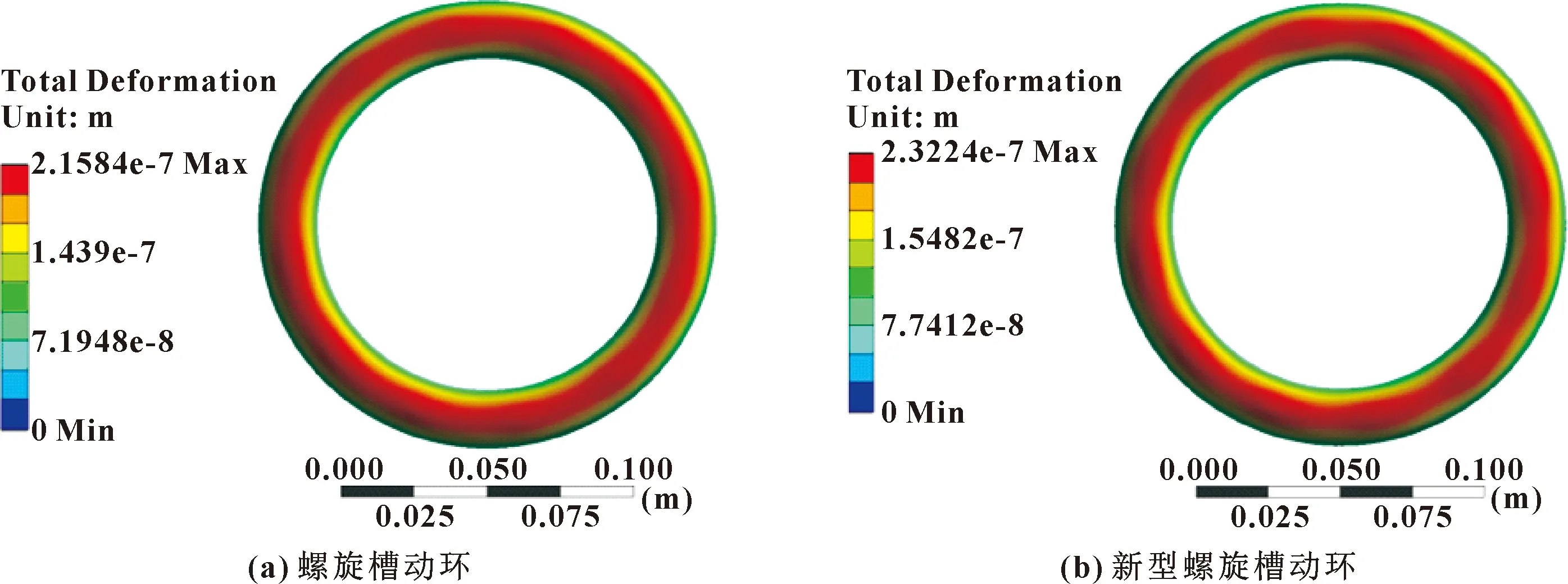
图16 2种槽型动环最大变形分布

由图16可知，新型螺旋槽动环的变形量大于传统螺旋槽动环的变形量,并且2种槽型发生变形最大的部位均在槽根处。这是因为干气密封在运行过程中，槽根部所形成的气膜压力最大，应力集中现象明显。传统螺旋槽动环的最大变形量约为0.216 μm，新型螺旋槽动环的最大变形量约为0.232 μm。这是由于新型螺旋槽槽根部相比传统螺旋槽具有较好的动压效应，产生了更大的气膜力，故使得新型螺旋槽动环的变形量大于传统螺旋槽。但总体来看，2种槽型的动环变形量不大，均在允许变形范围内。

5.2.2 干气密封静环流固耦合变形分析

图17所示为2种槽型干气密封静环的流固耦合变形云图。

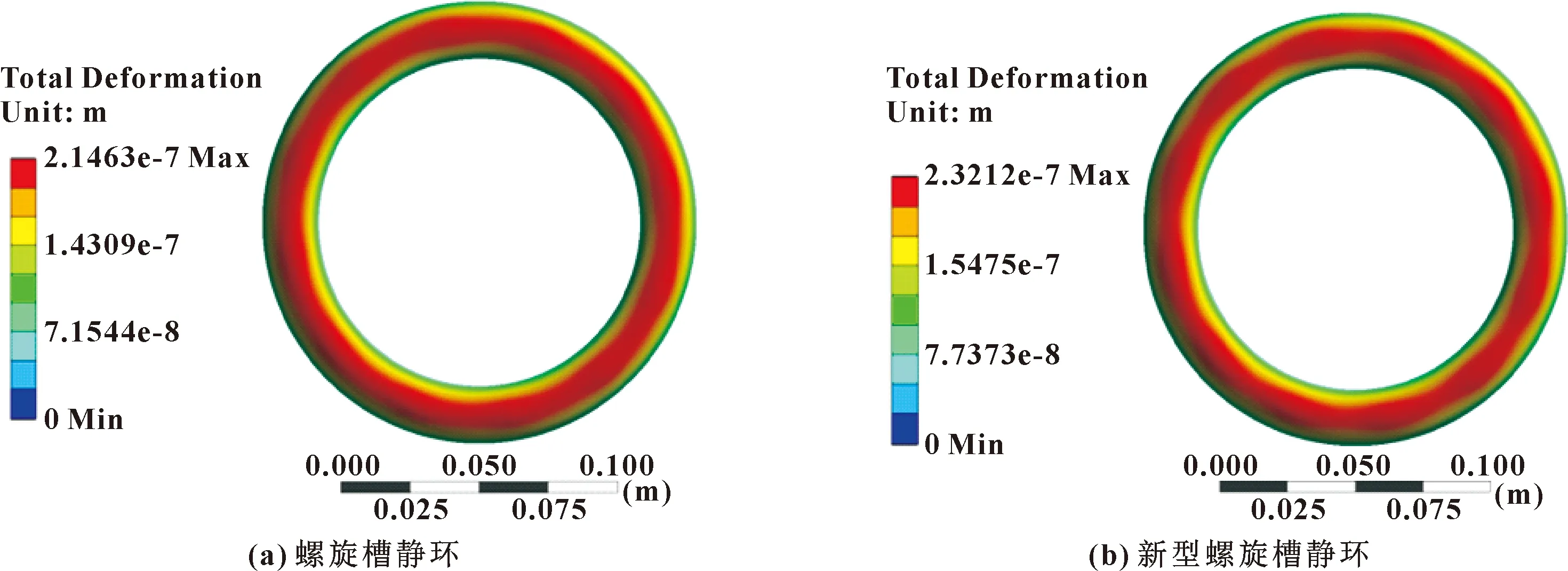
图17 2种槽型静环最大变形分布

由图17可知，传统螺旋槽静环的变形量约为0.214 μm，新型螺旋槽静环的变形量约为0.231 μm，相比图16所示的动环变形量，在该工况下，传统螺旋槽与新型螺旋槽的动静环变形量差别甚微，动环变形略大于静环变形。这是由于在干气密封运转过程中，静环保持不变，动环旋转产生更大的气膜力使其发生变形。

5.2.3 转速对干气密封环流固耦合变形的影响

图18所示为不同转速下对干气密封动、静环变形的影响。

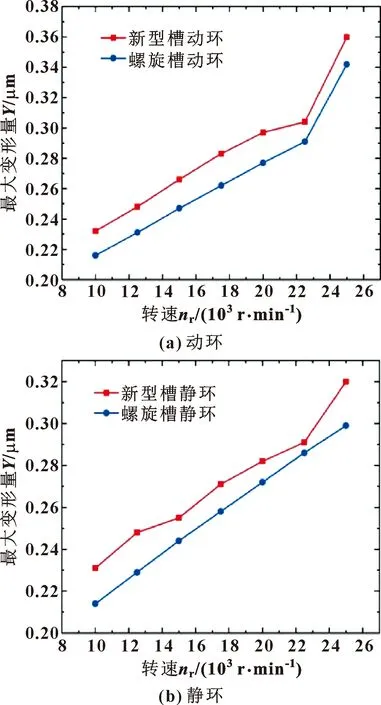
图18 不同转速对2种槽型动静环最大变形的影响

由图18可知，无论是哪种槽型，随着转速的增加，动、静环的变形量均增大。当转速为10 000 r/min时，传统螺旋槽静环变形量约为0.214 μm，动环变形量约为0.216 μm;新型螺旋槽静环变形量约为0.231 μm，动环变形量约为0.232 μm。当转速升高至25 000 r/min时，传统螺旋槽静环变形量约为0.3 μm，动环变形量约为0.34 μm;而新型螺旋槽静环变形量约为0.32 μm，动环变形量约为0.36 μm。在23 000 r/min后，两槽的动环变形量急剧增大，说明密封环的变形对于高转速较为敏感。而2种槽型的动、静环的变形量均随着转速的增加而增大，这也同时印证了应力随着转速的增加而增加的趋势,从而说明了干气密封动静环的变形也是由于流场中的应力所致。综合分析得知，新型螺旋槽的动静环变形量始终大于传统螺旋槽,这是由于新型螺旋槽槽根部具有较强的动压效应。随着转速的增加，无论是传统螺旋槽还是新型螺旋槽，动环的变形量始终大于静环的变形量。

5.2.4 入口压力对干气密封环流固耦合变形的影响

图19所示为2种干气密封槽型动、静环变形随着入口压力的变化曲线。可知，2种槽型的动、静环的变形量均随着入口压力的增加而增大，并且变化趋势与应力随着入口压力的变化趋势相似。当入口压力为1.25 MPa时，传统螺旋槽的动环变形量约为0.255 μm，静环变形量约为0.253 μm;新型螺旋槽动环变形量约为0.275 μm，静环变形量约为0.272 μm。当入口压力增大至2.75 MPa时，传统螺旋槽动环变形量约为0.5 μm，静环变形量约为0.48 μm;新型螺旋槽的动环变形量约为0.55 μm，静环形变量约为0.49 μm。