混合润滑下粗糙表面的接触刚度研究*
2022-09-21马欢景卉
马 欢 景 卉
(1.西安交通大学航天航空学院 陕西西安 710048;2.兰州大学管理学院 甘肃兰州 730000)
机械结合面是机械装备中各零部件之间的接触表面,对于各种高精密设备,结合面的接触刚度对设备的精度和性能有着重要影响。通常情况下,为了减少磨损,提高设备使用寿命,结合面往往都处于润滑状态[1]。机械结合面一般可以等效为2个粗糙表面之间的接触,因此,润滑状态下的粗糙表面间接触刚度的研究意义重大。
自经典赫兹接触[2]被提出以来,国内外学者对粗糙表面之间的接触进行了广泛研究[3-10]。其中以GREENWOOD-WILLIAMSON(G-W)模型[3]为代表的统计学接触模型和Persson接触理论[5]为代表的分形接触模型被广泛认可。在G-W模型中,两个粗糙面之间的接触往往等效为一个刚性平面和一个弹性粗糙表面之间的接触,粗糙面由曲率相同的球面组成,且其高度服从高斯分布。但由于粗糙表面的多尺度特征,统计学模型会受仪器分辨率的影响。为了更好地表征粗糙表面的多尺度特征,PERSSON[5]通过引入放大率概念,发展了一种基于压力扩散方法的随机粗糙表面接触理论。然而,上述模型仅仅考虑了干接触条件下的粗糙表面接触,没有考虑润滑对接触特性的影响。
在实际工业应用中,各种齿轮、轴承等机械系统以混合润滑接触方式工作,以减少摩擦或磨损。超声反射法是实验测量界面接触刚度的主要手段。GONZALEZ-VALADEZ等[11]利用超声技术测量了润滑界面接触刚度。然而,基于超声反射法测得的润滑粗糙界面的接触刚度远大于实际值[12]。因此,研究一种理论模型预测混合润滑状态下的接触刚度是非常必要的。
本文作者提出了一个混合润滑状态下粗糙表面的接触刚度等效薄层模型,研究了不同实际接触面积下,表面形貌和润滑剂对法向接触刚度的影响,为研究混合润滑状态下粗糙界面的接触特性提供了理论基础。
1 混合润滑状态下的接触刚度模型
1.1 模型描述
润滑状态下的粗糙接触界面由粗糙峰和周围的润滑剂组成,如图1所示。对于混合润滑粗糙界面,界面刚度由固体刚度和润滑剂刚度2部分组成,且其刚度关系符合弹簧并联准则,即
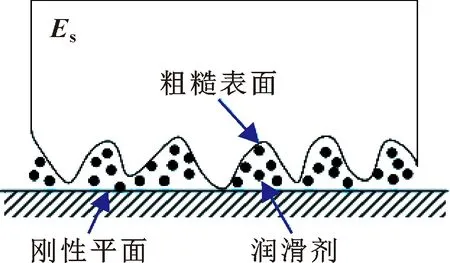
图1 混合润滑状态下的粗糙界面
Kn=Ks+Kl
(1)
式中:Kn为润滑状态下粗糙界面总接触刚度;Ks为固体刚度;Kl为润滑剂刚度。
对于弹性润滑界面,假设等效薄层与接触固体和平坦刚性表面刚性连接,如图2所示。因此,单位标称接触面积的法向接触刚度[12]可以表示为

图2 混合润滑接触等效薄层示意
(2)
式中:H0为等效薄层厚度,基于粗糙统计理论,H0一般取值为3倍的均方根粗糙度[13];E0为等效弹性模量,可表示为
E0=φ1Es+φ2Bl
(3)
式中:Es为固体的弹性模量;Bl为润滑剂的体积模量;φ1、φ2分别为等效弹性模量中固体和润滑剂的贡献比例,并满足
φ1+φ2=1
(4)
因此,固体刚度和润滑剂刚度可分别表示为
(5)
(6)
1.2 润滑接触刚度表达式
文中推导润滑接触状态下界面接触刚度的表达式。首先,基于WANG等[8]提出的干接触时粗糙表面增量接触模型推导得到单位标称面积固体接触刚度表达式为
(7)
式中:A0为标称接触面积;A(z)和N(z)分别为当粗糙界面分离为z时,粗糙表面的实际接触面积和等效圆斑数量。
将式(7)代入式(5)可得固体部分的贡献比例φ1为
(8)
将式(8)代入式(4)可得润滑剂部分的贡献比例φ2为
(9)
将式(8)和式(9)代入式(3)可得润滑接触等效弹性模量E0为
(10)
将式(10)代入式(2)可得润滑接触界面法向刚度Kn为
(11)
将式(9)代入式(6)可得润滑剂刚度Kl为
(12)
尽管固体的弹性模量远远大于润滑剂的体积模量,润滑剂对刚度的贡献也不可忽略,因为在粗糙峰初始接触时,固体的贡献比例接近于0,而润滑剂贡献比例接近于1。
2 结果和讨论
2.1 混合润滑状态下接触刚度
根据1.2节中润滑接触状态下界面接触刚度模型,只需粗糙表面的高度节点信息,便可预测混合润滑状态下接触刚度的演化。首先,通过PSD法在MATLAB中生成一个100 μm×100 μm的随机粗糙表面,其节点高度信息如图3所示。粗糙表面的具体参数为:σ=3 μm,Es=115.4 GPa,Bl=1.45 GPa,H=0.8,ν=0.3,其中H为赫斯特指数,ν为泊松比。基于以上信息,利用等效薄层模型数值求解混合润滑状态下接触刚度。如图4所示,随着实际接触面积的增大,接触刚度近似线性增加,与G-W模型[3]和Persson接触理论[5]所得到的线性关系一致。对于相同的实际接触面积,有润滑剂界面的接触刚度大于无润滑剂界面的接触刚度。固体和润滑剂分别对总接触刚度的贡献比例随着实际接触面积增大的变化规律如图5所示。初始接触时φ2>φ1,润滑剂作用占主导地位,但随着实际接触面积的增大,固体接触刚度逐渐超过润滑剂接触刚度占据主导地位。这说明在小载荷下,润滑剂的接触刚度对于总接触刚度具有重要意义。

图3 粗糙表面形貌

图4 有无润滑剂条件下接触刚度与面积比的关系

图5 固体和润滑剂的贡献比例与面积比的关系
2.2 润滑剂类型对混合润滑接触刚度的影响
为了研究润滑剂类型对混合润滑接触刚度的影响,文中比较了2种不同类型的润滑剂对接触刚度的影响。润滑剂在环境压力下的体积模量为
Bl=Bl0e-βkT
(13)
式中:Bl0为环境压力下温度为0 K时的体积模量;βk为泰特-杜利特尔常数;T为绝对温度。
表1列出了分析中使用的2种润滑剂的相关参数[14]。

表1 环境压力下润滑剂的参数[14]
图6(a)和图6(b)示出了在分别使用T9油和甘油2种润滑剂下,总接触刚度、固体接触刚度和润滑剂接触刚度随实际接触面积的变化规律。可知,总接触刚度、固体接触刚度随着实际接触面积的增大而增大,且总接触刚度总是大于固体接触刚度,而润滑剂接触刚度基本保持不变,并且在小载荷下润滑剂接触刚度大于固体接触刚度。通过对比2种不同的润滑剂,可以发现润滑剂的体积模量越大,混合润滑接触刚度增大越明显,润滑剂接触刚度占主导地位的范围也越大,这与实际情况是一致的。
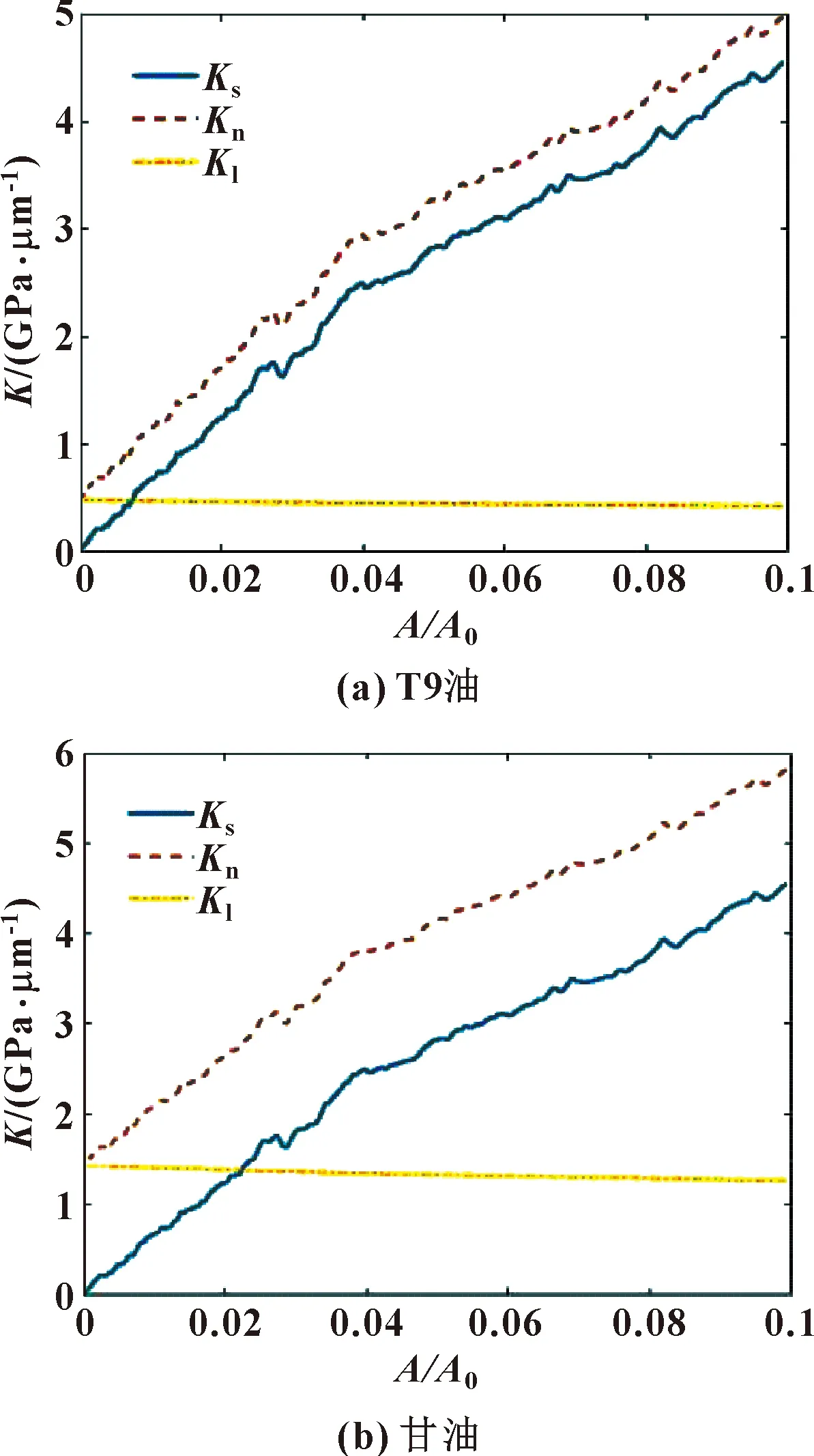
图6 不同润滑剂下法向接触刚度与面积比的关系
2.3 表面形貌对混合润滑接触刚度的影响
为了探究表面形貌对混合润滑接触刚度的影响,通过PSD法生成了3种不同粗糙度的随机粗糙表面,具体参数见表2。表面形貌对T9油润滑界面接触刚度的影响如图7所示,不同粗糙度的润滑界面的法向刚度均随着实际接触面积的增大而增大。在实际接触面积相同的情况下,更光滑的表面会产生更大的接触刚度。

表2 不同表面形貌的具体参数

图7 表面形貌对混合润滑接触刚度的影响
3 模型对比
为了验证文中提出的接触刚度模型的准确性,将文中模型与文献[13]的模型进行了比较。选用的参数为σ=2.04 μm,Es=115.4 GPa,Bl=1.45 GPa,H=0.7,ν=0.3。如图8所示,当实际接触面积相同时,文中模型的预测结果与文献[13]的模型的计算结果具有良好的一致性,证明了文中提出的混合润滑状态下粗糙界面的法向接触刚度模型的合理性与有效性。与现有模型相比,文中模型的创新之处在于只需要提供粗糙表面的高度信息,便可以简单准确地预测干接触和润滑接触时接触刚度随实际接触面积的演化。
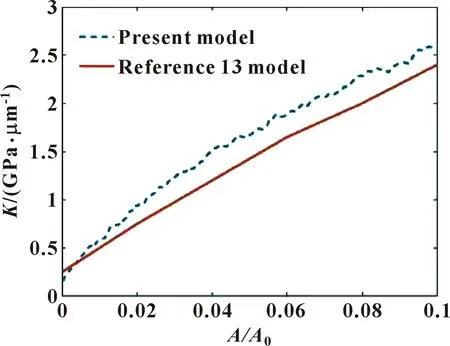
图8 不同模型法向接触刚度与面积比的关系
4 结论
通过提出一种等效薄层模型解决混合润滑状态下粗糙界面接触刚度的预测问题,将接触界面的总刚度等效为固体接触刚度和润滑剂接触刚度之和,从理论上估算了混合润滑法向接触刚度与实际接触面积的关系。主要研究结果如下:
(1)粗糙界面的法向接触刚度随法向载荷的增加而增加,且混合润滑状态下的接触刚度大于干接触条件下的接触刚度。
(2)在初始接触时,粗糙界面的法向刚度主要受润滑剂性能影响,随着实际接触面积的增大,固体刚度逐渐占据主导地位,表面形貌对法向接触刚度的影响变得更加明显,润滑剂的影响越来越小。
(3)建立的模型的预测结果与经典模型计算结果具有良好的一致性,验证了建立的模型的正确性。
