牙膏灌装机构设计及流动特性分析

徐锦华，黎光辉，孟爽，张炜

牙膏灌装机构设计及流动特性分析

徐锦华1，黎光辉2，孟爽2，张炜3

（1.陕西开放大学，西安 710119；2.哈尔滨商业大学 轻工学院，哈尔滨 150028；3.浙大宁波理工学院，浙江 宁波 315100）

通过设计双头平推柱塞式灌装机构，进一步提升牙膏等黏稠膏体的灌装生产效率，同时研究牙膏流变特性对灌装推力的影响，以解决当前牙膏等粘稠膏体灌装速度、精度低等问题。首先选取市场占有率较高的品牌牙膏进行流变试验，然后采用经典非牛顿流体本构方程拟合获得流变曲线，最后采用数值模拟物料灌装挤出过程，获得所需要的最大灌装推力。研究表明，牙膏属于非牛顿流体且具有剪切稀化的流变特性，与幂律流变模型（Powder Law黏度模型）拟合相关性为0.999 2。在最大灌装容量为200 mL、最大灌装速度为0.337 m/s时，所需推力为1 681 N。可为非牛顿流体的灌装机构设计提供理论指导。

牙膏；柱塞；灌装；流变性；流速；压力

牙膏灌装机构是牙膏灌装封尾机中的核心部件，其灌装速度、灌装精度对设备的整体性能有着重要影响。像牙膏等黏稠膏体在自然状态下的流动性比较差，对牙膏灌装输送必须依靠外力才能实现其更好的流动，因此在实际生产中对其进行灌装输送具有一定的难度[1]。柱塞式灌装机构因其具有良好的定量灌装以及输送特性，被广泛地应用于牙膏等黏稠物料的灌装[2-5]。柱塞式灌装机构的类型一般有3种类型，分别为竖直式、平推式和斜推式，三者主要的区别在于柱塞缸的放置形式不同，而工作原理基本一致。为了能够实现牙膏的精确灌装和高速生产，文中设计出新型平推式牙膏灌装机构，并对灌装牙膏的流动状态进行受力仿真分析，以此对灌装机构进行有效的改善，并保证设备的正常运行。

牙膏是由多种物质组成的一种复杂混合膏状流体，在灌装流动过程中具有较复杂的流变性，大多数学者都是利用黏度计的不同转速来检测牙膏的黏度值，以此对牙膏的流动特性进行研究分析。李劲峰等[6]利用美国BROOKFIELD，型号为DV3TRV流变仪来探究牙膏的流变特性，但只是以8组不同转速依次对牙膏进行黏度测试，发现牙膏体现出非牛顿流体的假塑性。徐钢等[7-9]为了探索测量牙膏黏度的方法，利用布氏黏度计（Brookfield)测量牙膏或其成分在不同转速下的黏度变化，发现在转速变大时牙膏的黏度会相应变小。李江平[10]为了探究牙膏的流变特性，利用了流变仪对3种不同配方的牙膏进行了流变性能的测试，结果表明牙膏在剪切速率增加时都有黏度下降的变化趋势。Ahuja等[11]为了预测牙膏泵送和挤压压力的流变学测量，建立了从流变学数据计算牙膏生产过程的泵送压力和挤压压力的精确方法。基于笔者的前期研究，为了简化牙膏的灌装流动分析，经过试验验证，若把牙膏黏度的测量以及灌装流动仿真当作牛顿流体进行仿真计算模拟时，按照一个灌装头每分钟生产80支牙膏，灌装容量为200 mL进行参数设置，牙膏生产需要非常大的灌装推力，这显然与实际工程应用是不相符的。

文中将基于牙膏柱塞式灌装机构的设计，利用旋转流变仪对牙膏进行流变试验，根据试验结果对牙膏试验数据进行非牛顿流体曲线拟合，再根据拟合得到的流变参数对牙膏进行柱塞式灌装流动仿真分析。依据仿真结果深入分析牙膏非牛顿流体灌装流动过程中内流场的特性变化规律，并计算出柱塞式灌装机构在不同灌装速度下对牙膏灌装需要施加的推力大小，以此为牙膏灌装机构的设计提供更加合理的科学依据和运行方案。

1 转阀柱塞式灌装机构的设计

1.1 灌装机构工作原理

牙膏柱塞式灌装机主要由柱塞缸、活塞、料筒、灌装阀外体、三通转阀、灌装嘴以及堵嘴杆等零部件组成。文中设计的柱塞式灌装机构采用平推式的结构类型，双头灌装，最大灌装速度为160支/min，最大灌装量可达200 mL。牙膏灌装机构的三维结构图见图1a，其驱动方式为通过伺服电机带动滚珠丝杠的上下运动，从而使灌装活塞在柱塞缸内往复运动，实现黏稠物料的定量灌装。活塞向左运动为黏稠物料的吸料过程，此时三通转阀的固定流道口与膏体入口相通；活塞向右运动为黏稠物料的排料灌装过程，此时三通转阀的固定流道口与灌装出口的流道相通。三通转阀的主要作用是实现灌装流道口的切断与导通，从而实现灌装膏体的吸料与排料过程。三通转阀的转动是通过主轴的伺服电机传入，然后再通过摆杆凸轮机构实现三通转阀的运动控制。对于黏稠物料的灌装，灌装完成后容易在灌装嘴出口处发生膏体滴漏或者产生拉丝的情况，因此在灌装嘴流道中需要有灌装堵杆机构。灌装堵杆为中心导通的空管件，能够防止膏体的滴漏，而且堵杆中心的导空管道通过外接导管连接气泵，在每完成一件产品的灌装时，通过在灌装嘴口处吹气，能够防止黏稠膏体产生拉丝的现象。灌装机构的流道剖视结构见图1b。

1.料筒；2.柱塞缸；3.三角摆臂；4.滚珠丝杠；5.伺服电机；6.摆杆；7.摆杆凸轮；8.气缸；9.转阀拨杆；10.灌装头；11.软管提升机构；12.牙膏入口；13.灌装推杆；14.活塞；15.转阀；16.气缸；17.堵杆；18灌装嘴。

1.2 灌装机构工作循环图

灌装机对牙膏进行定量灌装需要多个机构协同动作，柱塞缸容腔内吸满牙膏，三通灌装阀开启，软管提升到位，灌装堵杆提升开启灌装嘴口，对牙膏进行灌装。基于前面灌装机的工作原理以及结构特点，完成牙膏灌装机的工作循环图设计，见图2。灌装机构采用伺服电机驱动，通过滚珠丝杠、连杆等机构的传动，实现牙膏的吸料与排料。摆杆凸轮机构可控制三通转阀的导通与闭合，以此进行牙膏流道口的切断，从而实现牙膏的精确定量灌装。软管提升机构采用伺服电机与同步带传动相组合，实现牙膏软管边灌装边下降，以防止灌装牙膏在管内产生空段。灌装嘴杆堵漏机构采用短行程小气缸与摆杆机构实现，防止灌装牙膏后产生滴漏或拉丝。

图2 牙膏灌装机工作循环图

1.3 流体域模型

基于前面灌装机构的设计，利用Inventor软件创建出牙膏灌装管道的流体域三维模型（见图3），流体域模型创建过程中需要对流体域三维结构的连接处进行平滑等处理，以保证仿真计算的收敛性，其中流体域在柱塞缸内的直径为55 mm、倾斜流道直径为15 mm、灌装嘴口径为11 mm。由此可知，在整个流体域中，柱塞缸流道截面积最大，灌装嘴口处的截面积最小，其次较小的为斜管流道的截面。

图3 流体域三维模型

2 牙膏流变性的研究与分析

牙膏的黏度与稠度存在一定的正比关系，一般情况下牙膏的稠度越高，其黏度就越大[12]。自1995年，国家标准中取消了牙膏黏度指标，描述指标改为稠度，但现阶段对牙膏进行流变特性研究和仿真模拟流动等试验仍以黏度为描述对象。基于文中前期采用NDJ–1型旋转式黏度计和CAP 2000+锥板黏度计测量牙膏黏度，发现如直接采用某一转速测量得到的黏度，并以牛顿流体模型进行模拟计算得到的灌装推力非常大，这显然是不对的。结合前期试验以及多位学者的研究可知，牙膏属于非牛顿流体中的假塑性流体，若以旋转黏度计以不同转速测量得到的不同黏度来拟合牙膏的流变曲线，得到的曲线不够平滑，黏度值波动较大，拟合得到的流变方程必定存在较大的误差。为了准确探究牙膏的流变性，文中选择市场上占有率较大的牙膏A做流变试验，采用赛默飞Mars40旋转流变仪对其进行流变试验，并经实验测得牙膏的密度为1 231 kg/m3。

2.1 流变试验

试验采用赛默飞Mars40旋转流变仪测量牙膏的流变曲线。在试验过程中，不同的剪切速率对应不同膏体的流动过程，通过旋转流变仪可以得到所测量膏体的剪切黏度随着剪切速率变化的曲线，根据实验结果得到的数值点以及流变曲线可以拟合出每种膏体对应的本构方程。牙膏流变试验的流程步骤见图4。

通过赛默飞Mars40旋转流变仪分别测量得到某品牌牙膏的流变曲线，见图5。流变试验温度控制为室温（25 ℃），选择直径为25 mm的平行板，旋转模式，剪切速率对数变化范围为0.01～1 000 s−1。

从图5c中可以看到，牙膏的黏度是随着切剪速率的增大而呈现逐渐变小的趋势，由此可以得到牙膏属于非牛顿流体中的剪切稀化流体。

2.2 牙膏流变方程拟合

为了能够准确地拟合出适合描述牙膏的流变方程，文中尝试根据流变试验得到的数据拟合非牛顿流体中的剪切稀化流变方程。文中采用了幂律流变模型（Powder Law黏度模型）[13]、赫谢尔–巴尔克利（Herschel–Bulkley）流变模型[14]、Cross黏度模型[15]、Ellis黏度流变模型[16]以及Carreau黏度模型[17]对牙膏试验数据进行了流变曲线的拟合。在曲线拟合过程中发现采用Cross黏度模型、Ellis黏度流变模型以及Carreau黏度模型进行拟合时存在拟合失败或者无法拟合的现象，因此文中主要分析采用Powder Law黏度模型与Herschel–Bulkley流变模型拟合得到的流变方程。

其中Power Law流变模型中黏度与剪切速率的流变方程为：

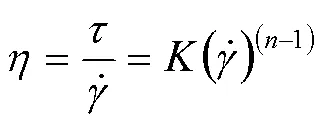
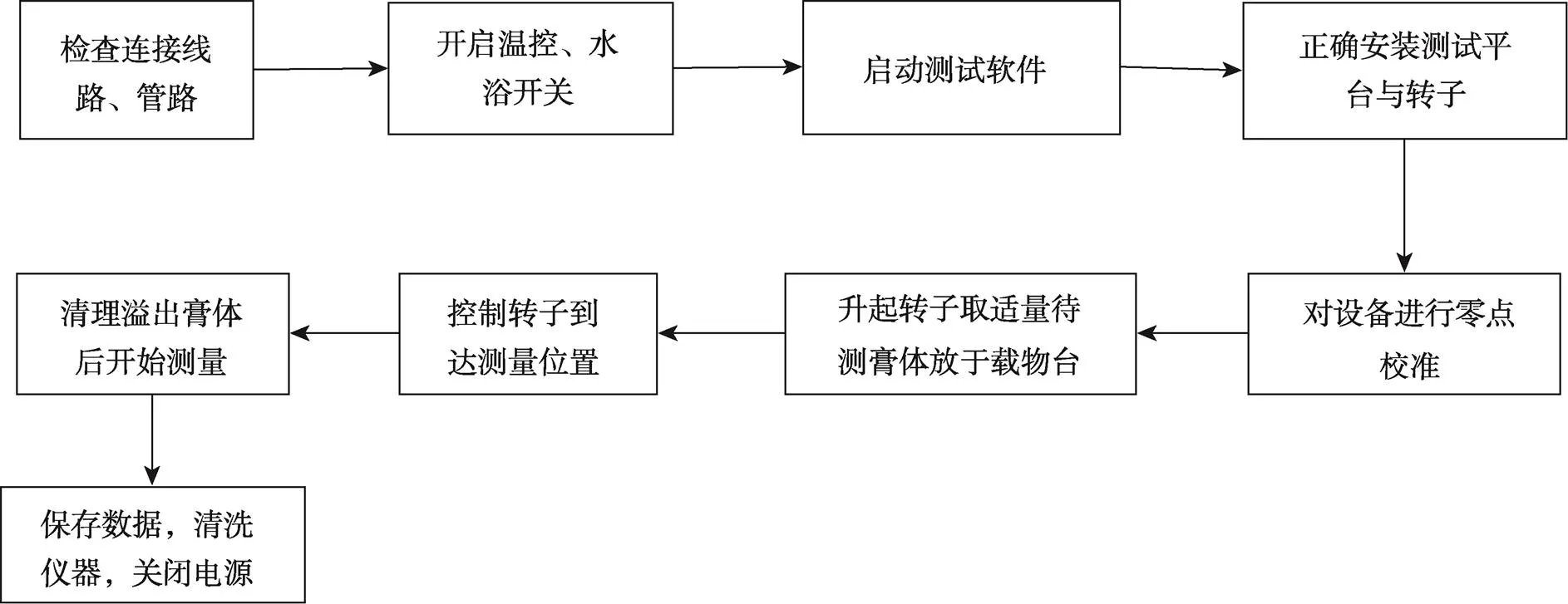
图4 牙膏流变实验步骤

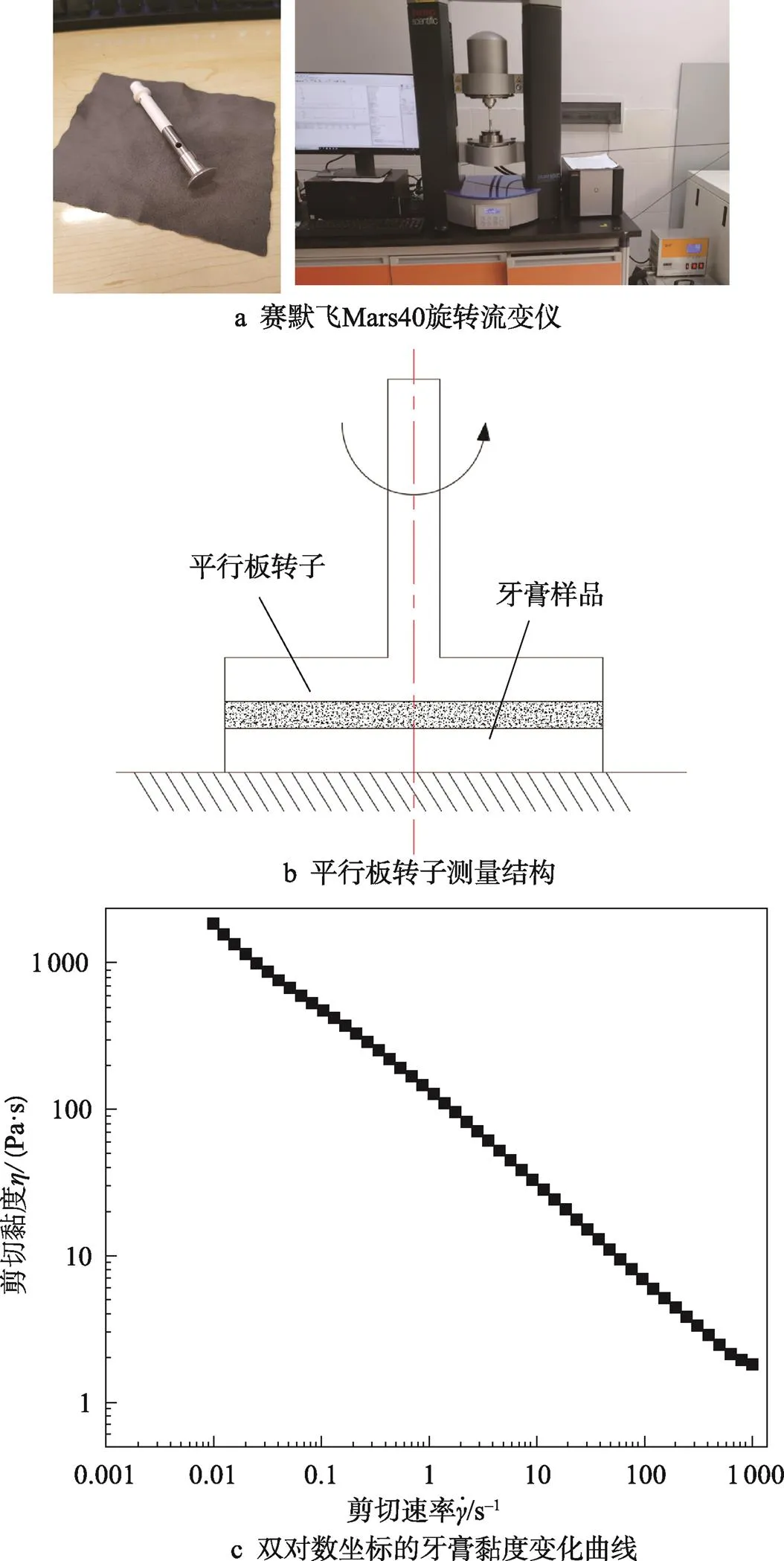
图5 牙膏流变试验仪器与流变曲线

Herschel–Bulkle流变方程为：

采用Powder Law黏度模型与Herschel–Bulkley黏度模型对牙膏流变方程的拟合效果见图6。

从牙膏流变方程曲线拟合来看， Powder Law黏度模型与Herschel–Bulkley流变模型的拟合效果都很好，在剪切速率为0.01～1 s−1时，Powder Law黏度模型与Herschel–Bulkley黏度模型的曲线拟合效果相差不大，而在剪切速率在1～1 000 s−1时，Powder Law黏度模型的拟合效果相对更好一些，并且在膏体灌装过程中牙膏的剪切速率基本上都大于1 s−1。从整体的拟合效果来看，Powder Law黏度模型的拟合相关性（2）为0.999 2，Herschel– Bulkley黏度模型的拟合相关性（2）为0.999 02。根据式（2）可拟合得到牙膏的Powder Law黏度流变方程为：

根据式（4）可拟合得到牙膏的Herschel–Bulkley黏度流变方程为：

从式（5）—（6）的拟合效果可以看出，Powder Law黏度模型对牙膏的拟合效果比Herschel–Bulkley黏度模型的拟合要好，因此文中主要采用非牛顿流体中的Powder Law黏度模型对牙膏灌装流动进行仿真模拟分析。

图6 牙膏流变方程拟合

3 力学分析与流变特性分析

运用Fluent软件对牙膏进行灌装流动的仿真与计算分析，同时以牙膏A为灌装仿真的研究对象，并根据实验测量出牙膏的物性参数来定义灌装流体的相关属性，通过仿真分析牙膏在柱塞式灌装机构中的流速分布以及压力场的变化情况。

3.1 计算域与网格划分

在对牙膏灌装流体域进行流场分析时，考虑到流体计算域的三维模型较为复杂，为了网格划分方便，设置流体域划分的网格类型为非结构化网格中的Tetra/Mixed[18]。针对牙膏灌装流体域模型划分的网格数分别为187 816、263 960、506 748、1 175 377，计算迭代步数为200步，仿真模拟得到的最大压力以及最高流速见表1。

由表1可知，当划分的网格数量从187 816增加到1 175 377时，流场中的最大压力从0.697 MPa增加到0.718 MPa，增幅为3.01%；最大流速从11.2 m/s增加到11.3 m/s，增幅为0.89%。从网格对比验证分析可知，在该网格数量的变化范围内，流场的最大压力以及最大流速的变化都很小。当网格数量为263 960及以上时，仿真模拟得到的最大压力以及最大流速更加趋于稳定，考虑到仿真模拟计算需要的时间、计算结果的稳定性和工作量等因素，文中用于仿真模拟的网格数量为263 960。

表1 网格划分无关性验证的参数对比

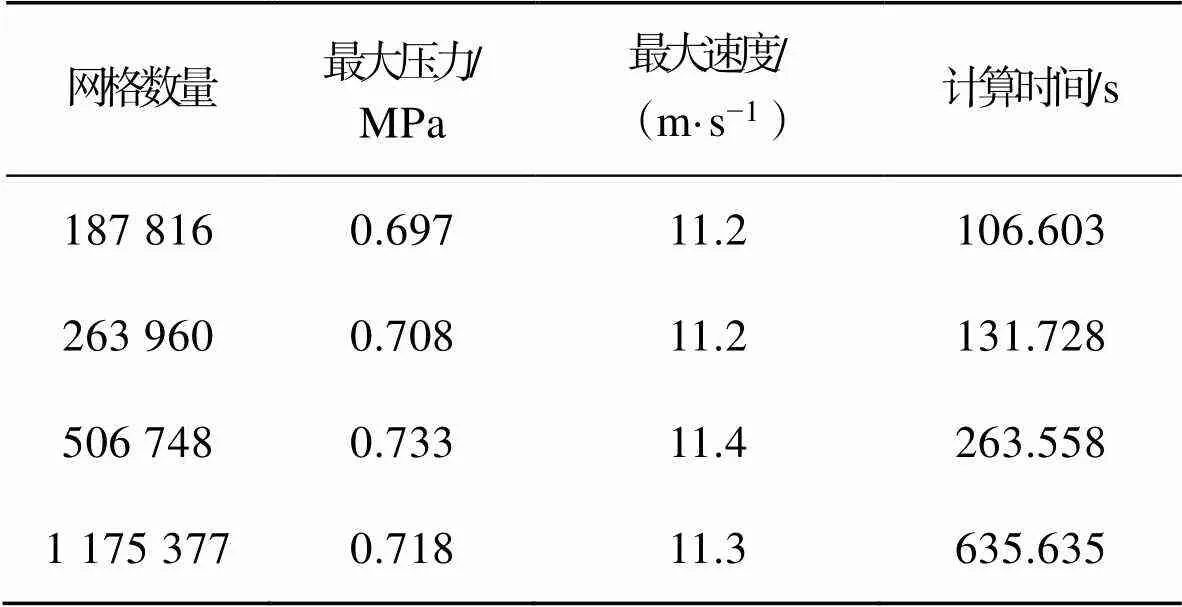
Tab.1 Comparison of parameters for grid division-independent validation

3.2 边界条件与参数设置

考虑到牙膏黏度较大以及灌装流速不高，文中采用层流模型（Laminar）对牙膏灌装流场进行模拟计算分析。设置牙膏密度为1 231 kg/m3，黏度选择非牛顿流体的Non–Newtonian Power Law模型，黏度系数以及幂指数根据流变方程拟合得到，最大、最小剪切黏度值根据流变试验测量得到。相关流变参数输入见图7，其中稠度系数为124.018，幂律指数为0.427，最大、最小剪切黏度值分别为1 830、1.823。边界条件的入口流速依次设定为0.337、0.294、0.253、0.210、0.168 m/s，近壁面处的速度为0，出口压力设置为大气压101.325 kPa。

图7 牙膏流变参数输入

3.3 仿真模拟结果分析

3.3.1 速度流场分布

根据前面设计的牙膏灌装机构为双头灌装，最大灌装容量为200 mL，最大速度为160支/min，并结合各动作机构的工作循环图，得到一个灌装嘴的最大灌装生产速度为0.337 m/s。牙膏灌装的流场分布可以直观地反映出速度流场结构，在最大灌装容量为200 mL、最大灌装生产速度为0.337 m/s的条件下，牙膏罐装速度流场分布见图8。其中柱塞缸端面处为进口速度，牙膏经过柱塞缸流向斜管流道，然后经过垂直流道往下流，垂直流道中心处有一灌装堵杆，最后牙膏从灌装嘴流出实现灌装。

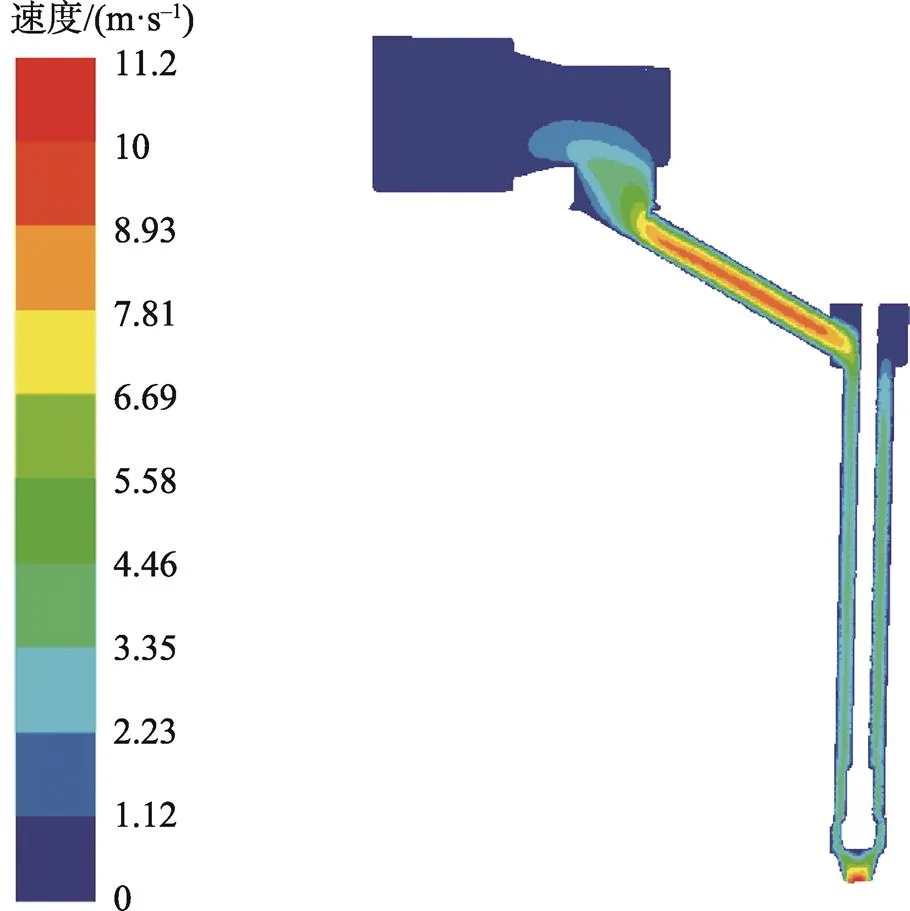
图8 牙膏灌装速度流场云图

从图8中可以发现，在整个流体域中牙膏的流速随着截面积的减小而呈现增大的趋势。柱塞缸内的流道截面积为最大，牙膏的流速基本上为最小的；牙膏从柱塞缸内流出到斜管流道内时流道的截面积发生较大的变化，牙膏灌装流速随着流道的变小而变大；从斜管流出的牙膏基本向垂直管道下方流动，最后从灌装嘴口处流出，而灌装嘴口处的截面积为整个流体域中最小的面积，因此灌装嘴口中心处的流速基本为最大流速。

3.3.2 速度流动特性

牙膏灌装过程中的流场速度矢量图见图9。从图9中可以发现，在整个流体域中，牙膏在一些边角区域基本不流动，甚至会产生微小的类似于旋转漩涡的流动现象。牙膏在同一截面的流动过程中，流道中心处的流速最大，近壁面的流速基本上接近于0，这与前面分析的牙膏属于非牛顿流体的剪切稀化特性基本吻合。牙膏在灌装流动过程中，近壁面的牙膏受到的剪切速率很小，因而具有较大的黏度，流动速度也就很缓慢。

图9 牙膏灌装速度流场矢量图

3.3.3 压力分布特性

如图10所示为灌装入口速度为0.337 m/s时整个流体域的压力云图。从压力云图中可知，牙膏从灌装入口到出口的压力呈现逐渐变小的趋势，在柱塞缸内的灌装压力最大为0.708 MPa。为了保证灌装机构设计的合理性，文中还对5种不同的灌装速度进行了流场压力模拟。当牙膏灌装生产速度分别为80、100、120、140、160支/min时的最大压力曲线变化见图11，其灌装入口对应的速度为0.168、0.210、0.253、0.294、0.337 m/s。从压力曲线图可知，灌装的生产速度越大，需要的灌装压力就越大。当灌装速度最大为0.337 m/s时，需要的最大灌装压力为0.708 MPa，由此可以计算出牙膏灌装需要的最大推力为：

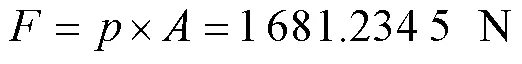
根据对牙膏最大灌装推力的计算模拟结果，能够为牙膏灌装机构的电机选型和结构优化设计提供很好的理论数据。

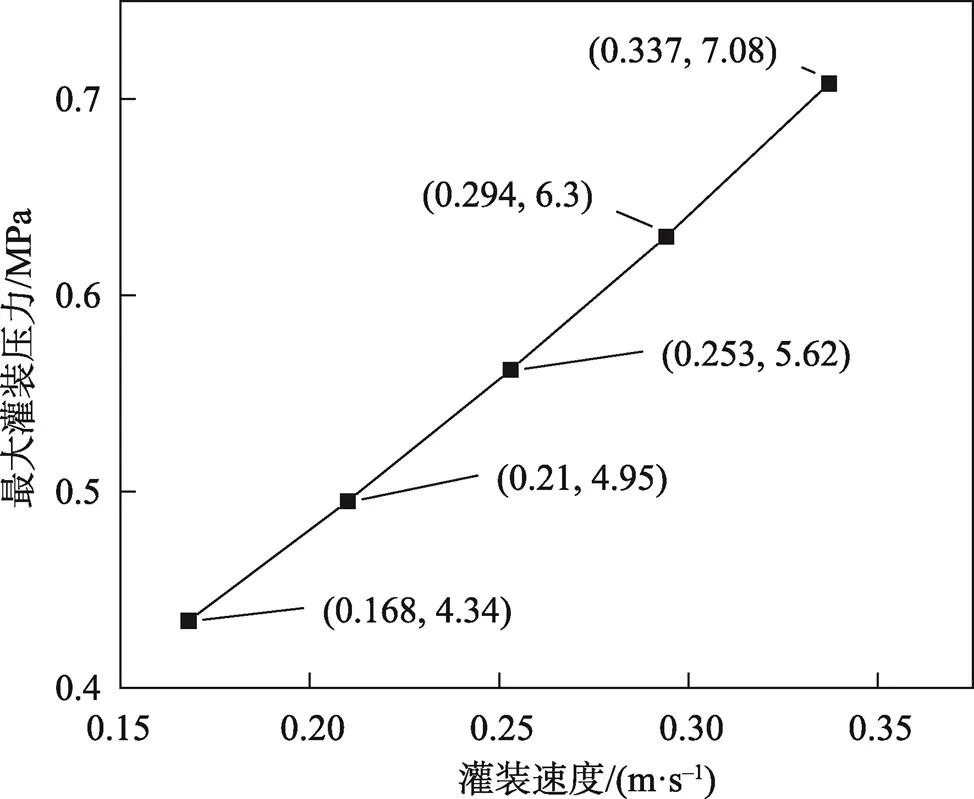
图11 灌装速度与最大压力关系曲线

4 结语

文中基于牙膏灌装的工作原理和工作循环图设计出新型双头牙膏灌装机构，同时为了设计的灌装机构能够满足工程应用，通过流变试验分析了牙膏的流变特性，并从流变实验结果中拟合出适合描述牙膏灌装流动特性的非牛顿流体的流变方程，再根据流变方程的相关流变参数对牙膏的灌装流动进行了流场模拟仿真分析，得到结论如下。

1）结构上，文中设计了新型双头平推柱塞式牙膏灌装机构，其中柱塞缸内径为55 mm，最小灌装嘴口直径为11 mm，能够满足牙膏A等黏稠膏体的灌装，灌装容量可达200 mL，灌装速度可达160支/min。

2）牙膏的流变特性对其灌装流动有着较大的影响，随着剪切速率的增大，牙膏的黏度呈现逐渐变小的趋势。从牙膏的流变试验以及流变方程拟合过程中发现，牙膏的流变性质与非牛顿流体中的幂律流变方程的拟合效果很好，具备剪切稀化的流变特性。通过流变试验对牙膏A进行幂律流变方程拟合，得到牙膏的稠度系数为124.018，流变幂指数为0.427。

3）在对牙膏进行灌装流动仿真模拟中发现，牙膏A的灌装生产速度从80支/min增加到160支/min时，产生的最大灌装压力从0.432 MPa增加到0.708 MPa，灌装推力从1 030.587 N增加到1 681.235 N，该数据能够为牙膏灌装机构的电机选型以及结构优化提供参考。

[1] LAREO C, FRYER P J, BARIGOU M. The Fluid Mechanics of Two-Phase Solid-Liquid Food Flows: A Review[J]. Food and Bioproducts Processing: Transactions of the Institution of of Chemical Engineers, Part C, 1997, 75(2): 79-105.

[2] 孟爽, 黎光辉, 刘松昀, 等. 塑料软管灌装封尾机的工艺分析及关键技术[J]. 包装工程, 2022(1): 42-51.

MENG Shuang, LI Guang-hui, LIU Song-yun, et al. Process Analysis and Key Technology of Plastic Hose Filling and Sealing Machine[J]. Packaging Engineering, 2022(1): 42-51.

[3] [杨福馨, 王生泽. 充填管口孔形对黏稠流体断流效果的影响研究[J]. 包装工程, 2010(17): 94-96.

YANG Fu-xin, WANG Sheng-ze. Influence Research of the Filling Orifice Shape on the Flow Break Effect of Viscous Fluid[J]. Packaging Engineering, 2010(17): 94-96.

[4] 吕帅, 张裕中. 高黏稠物料在灌装阀体内的流动状态分析[J]. 包装工程, 2012, 33(15): 10-15.

LYU Shuai, ZHANG Yu-zhong. CFD Analysis of High Viscous Material in Filling Piston[J]. Packaging Engineering, 2012, 33(15): 10-15.

[5] 王洪申, 张家振, 陈杰. 柱塞式调节阀壁面粗糙度对流量系数影响的数值模拟研究[J]. 流体机械, 2020, 48(9): 29-34.

WANG Hong-shen, ZHANG Jia-zhen, CHEN Jie. Numerical Simulation of Influence of Wall Roughness on Flow Coefficient of Plunger Regulating Valve[J]. Fluid Machinery, 2020, 48(9): 29-34.

[6] 李劲峰, 高鹰, 宁科功, 等. 透过流变学研究3种胶体对牙膏的影响[J]. 口腔护理用品工业, 2016, 26(3): 31-34.

Li Jin-feng, Gao Ying, Ning Ke-gong, et al. Study on the Effect of Three Colloids on Toothpaste by Rheology[J]. Toothpaste Industry, 2016, 26(3): 31-34.

[7] 徐钢. 利用布氏粘度计测量牙膏粘度方法的探索[J]. 口腔护理用品工业, 2013, 23(3): 29-30.

XU Gang. Exploration on the Method of Measuring Toothpaste Viscosity by Brinell Viscometer[J]. Toothpaste Industry, 2013, 23(3): 29-30.

[8] 孙志勇, 沈兆雷, 龙秀茹. 牙膏中常用胶体的分析[J]. 口腔护理用品工业, 2016, 26(1): 9-12.

SUN Zhi-yong, SHEN Zhao-lei, LONG Xiu-ru. Analysis of Colloids Commonly Used in Toothpaste[J]. Oral Care Industry, 2016, 26(1): 9-12.

[9] 袁发贵, 章金宇. 不同取代度羧甲基纤维素钠对牙膏性能的影响[J]. 口腔护理用品工业, 2020, 30(3): 14-17.

YUAN Fa-gui, ZHANG Jin-yu. Effect of Sodium Carboxymethyl Cellulose with Different Substitution Degree on Toothpaste Performance[J]. Toothpaste Industry, 2020, 30(3): 14-17.

[10] 李江平. 全山梨醇配方在牙膏中应用的研究[J]. 牙膏工业, 2006(2): 12-13.

LI Jiang-ping. Study on the Application of Total Sorbitol Formula in Toothpaste[J]. Toothpaste Industry, 2006(2): 12-13.

[11] AHUJA A, LUISI G, POTANIN A. Rheological Measurements for Prediction of Pumping and Squeezing Pressures of Toothpaste[J]. Journal of Non-Newtonian Fluid Mechanics, 2018, 258: 1-9.

[12] 马萱, 汪发文. 牙膏国家标准新旧版本对比及与国际标准的对比[J]. 牙膏工业, 2003(1): 19-26.

MA Xuan, WANG Fa-wen. Comparison between New and Old Versions of National Toothpaste Standards and International Standards[J]. Toothpaste Industry, 2003(1): 19-26.

[13] 李亚飞, 周懿, 胡钺, 等. 基于COMSOL的非牛顿流体在管道中的流动特性研究[J]. 科技与创新, 2020(5): 21-25.

LI Ya-fei, ZHOU Yi, HU Yue, et al. Study on Flow Characteristics of Non-Newtonian Fluid in Pipeline Based on COMSOL[J]. Science and Technology & Innovation, 2020(5): 21-25.

[14] ESTELLÉ P, LANOS C, PERROT A. Processing the Couette Viscometry Data Using a Bingham Approximation in Shear Rate Calculation[J]. Journal of Non-Newtonian Fluid Mechanics, 2008, 154(1): 31-38.

[15] CROSS M M. Rheology of Non-Newtonian Fluids: A New Flow Equation for Pseudoplastic Systems[J]. Journal of Colloid Science, 1965, 20(5): 417-437.

[16] MATSUHISA S, BIRD R B. Analytical and Numerical Solutions for Laminar Flow of the Non-Newtonian Ellis Fluid[J]. AIChE Journal, 1965, 11(4): 588-595.

[17] SCOTT B, PHILIPPE V, PUNIT K, et al. Comment on ''History, Origins and Prediction of Elastohydrodynamic Friction'' by Spikes and Jie[J]. Tribology Letters, 2015, 58(1): 1-25.

[18] 张浩, 陈为花, 包晓琳, 等. 螺旋管内幂律流体流动换热数值模拟[J]. 山东建筑大学学报, 2021, 36(3): 1-8.

ZHANG Hao, CHEN Wei-hua, BAO Xiao-lin, et al. Numerical Simulation of Heat Transfer Characteristics of Power-Law Fluid Flow in Spiral Tube[J]. Journal of Shandong Jianzhu University, 2021, 36(3): 1-8.

Design and Flow Characteristics Analysis of Toothpaste Filling Mechanism

XU Jin-hua1, LI Guang-hui2, MENG Shuang2, ZHANG Wei3

(1. The Open University of Shaanxi, Xi’an 710119, China; 2. School of Light Industry, Harbin University of Commerce, Harbin 150028, China; 3. Ningbo Tech University, Zhejiang Ningbo 315100, China)

The work aims to design a double-head flat-push plunger filling mechanism to improve the filling and production efficiency of the viscous pastes, such as toothpaste and study the effect of the rheological characteristics of toothpaste on filling thrust at the same time, so as to solve the current problems of low filling speed and accuracy of toothpaste and other viscous pastes. Firstly, the toothpaste with high market share was selected for the rheological test, and then the rheological curve was fitted by the classical non-Newtonian fluid constitutive equation. Finally, the filling and extrusion process of material was simulated to obtain the maximum filling thrust required. According to the study results, toothpaste was a non-Newtonian fluid and had rheological properties of shear thinning. The correlation coefficient between the toothpaste and the power-law rheological model (Powder law viscosity model) was 0.999 2. At the maximum filling capacity of 200 mL and the maximum filling speed of 0.337 m/s, the required thrust was 1 681 N. The conclusion can provide theoretical guidance for the filling mechanism design of non-Newtonian fluid.

toothpaste; plunger; filling; rheological; flow rate; pressure

TB486；TB487

A

1001-3563(2022)17-0157-08

10.19554/j.cnki.1001-3563.2022.17.020

2022–01–15

宁波市公益类科技基金（202002N3082）

徐锦华（1966—），女，本科，副教授，主要研究方向为机械设计、焊接材料及加工工程。

责任编辑：曾钰婵