球体斜碰撞下包装材料能量传递及转换的试验研究
2022-09-21王庆朋李威王恒王振锋李德峰徐广印
王庆朋,李威,王恒,王振锋,李德峰,徐广印
球体斜碰撞下包装材料能量传递及转换的试验研究
王庆朋1,2,李威1,王恒1,王振锋1,2,李德峰1,徐广印1,2
(1.河南农业大学 机电工程学院,郑州 450002;2.农产品冷链物流信息与装备技术河南省工程实验室,郑州 450002)
针对在球体斜碰撞过程中,包装材料界面能量变化及其量化表征的问题,基于碰撞接触面的几何特征,提出外加能量吸收率、传递率和转换率的计算模型。首先,分析球体斜碰撞接触面的几何特征,利用基圆和滑移面面积建立能量吸收率、传递率,以及不同方向能量比率的数学表达式。然后,通过搭建球体自由跌落斜碰撞测试平台,分析冲击角、衬垫厚度、跌落高度、球体直径和材料密度对能量参量的影响。通过碰撞接触面积计算能量吸收率和转换率,遵循了能量守恒定律,具有可行性;能量吸收率在75%以上,并随着跌落高度、球体直径和密度增加而变大,而冲击角对能量吸收率的影响较小;法向能量比率随着冲击角增加、球体直径减小而下降,切向能量比率与此相反,跌落高度和密度对能量比率无明显影响;在给定工况下,衬垫的最佳吸能厚度为4 mm。文中的分析有助于包装材料碰撞界面处能量变化以及接触特性的研究。
包装材料;斜碰撞;接触面积;能量吸收;传递与转换
为了避免产品在流通过程中因受到振动和冲击等外加载荷作用而产生破损,合理的缓冲包装是必不可少的,这对整个系统的动态响应、接触表面摩擦和磨损等都有着重要影响[1-3]。
目前,针对碰撞界面问题已经有很多研究,主要研究方法有连续碰撞力和冲量动量等。在连续碰撞力方法中,经典的完全弹性接触模型不考虑能量消耗,是该类分析的基础[4]。在实际碰撞过程中,接触材料并不是完全弹性变形,而存在黏弹性、塑性等,耗散了一定能量。为了分析接触过程中能量变化,常将卸载视为弹性过程,加载和卸载曲线所围面积即为能量耗散[5-6]。球体接触状态从完全弹性变形发展为弹性–塑性→弹性–混合弹塑性–塑性→弹性–混合弹塑性→混合弹塑性,已有文献主要分析了冲击角、材料硬度和硬化指数等对能量耗散的影响[5-6]。上述研究方法的不足之处是不能较好地表达界面应力分布和变化过程,因此,数值方法在该研究领域得到广泛的应用。Messaadi等[7]利用有限元方法对球体在与重力方向呈30°、45°和60°夹角下进行斜碰撞分析,随着角度增加,球体接触时间减少,而接触面积和接触压力变大,等效剪切应力在夹角为45°时达到最大值,相应的磨损体积较大。Nishida等[8]对铝合金球体进行了超高速斜碰撞分析,当冲击角较小时,碰撞界面近似为圆形;而当冲击角大于40°时,则为类椭圆。类似地,Stropek等[3]、谢若泽等[9]和Key等[10]对梨、合金钢和复合材料等碰撞过程中能量耗散、损伤特性等进行分析。
基于动量冲量方法,主要考虑碰撞前后运动状态变化,应用比较广泛的模型有Walton、Maw和Stronge等。在碰撞界面不仅存在回弹作用,还存在黏着、滑动和滚动等[2,11-13],运动状态的变化由法向回弹系数和摩擦因数等表达,而黏着的程度由表面能等表达,进而分析系统的能量变化规律。Doménech-carbó等[2,13]采用独立摩擦回弹的建模方法,假定球体材料回弹和摩擦独立存在,能够同时考虑界面特征参量的变化。韩维等[14]基于瞬态摩擦和切向恢复系数,采用步进冲量方法求解斜碰撞问题。在试验方面,Dong等[15]通过钢球自由跌落斜碰撞前后运动状态,分析在不同冲击角下回弹系数和回弹角等变化,当冲击角大于20°时,界面状态从黏着发展为滑动。类似地,Cross等[16]、冯斌等[17]和Ireland等[18]对钢球、马铃薯和橡胶球等碰撞过程中回弹系数和能量耗散等进行了测试分析。
目前,关于球体与包装材料在外加载荷作用下的碰撞问题,研究者往往重视碰撞前后运动状态变化,而忽视界面处能量吸收、传递和转换过程;再者,斜碰撞界面存在滑移状态,Dong等指出[15],如何量化表征界面参量变化还存在问题。鉴于此,基于球体斜碰撞接触面的几何特征,提出外加能量在界面处的吸收率、传递率,以及不同方向上能量比率的数学表达式,通过搭建球体自由跌落碰撞测试平台,分析冲击角、衬垫厚度、跌落高度、球体直径和密度对能量参量的影响,为碰撞过程中包装材料界面能量变化和接触特性分析提供基础。
两组治疗有效率比较,实践组采取复方丹参滴丸与曲美他嗪联合应用治疗,实践组治疗有效率明显高于对照组,两组对比,差异有统计学意义(P<0.05)。见表1。
1 球体斜碰撞界面能量变化分析与表征
1.1 碰撞界面能量变化分析
具有一定能量的球体以冲击角与平板发生斜碰撞,如图1a所示,在接触界面处,一部分能量在法向转换为材料应变能,另一部分则在切向转换为应变能和摩擦耗能。当材料发生黏性、塑性变形和内部微观结构变化时,消耗相应的能量,在形式上表现为0
1.2 碰撞界面能量变化表征
为了分析球体斜碰撞过程中包装材料界面处能量吸收、传递和转换关系,通过接触面积进行表征计算。由于法向压缩和切向滑移,接触面形状既不是规则圆形,也不是椭圆,而是这两者的结合。实际接触面包括基圆和滑移面2部分,如图1b所示,基圆与2倍的滑移面面积之和为椭圆面积。通过采用分层材料的测试方案,即含有和去掉包装材料的2种形式,分别获得顶层和底层碰撞界面接触信息,进而计算相应的能量参量。在包装材料的顶层和底层界面处基圆面积分别为:

图1 球体斜碰撞及其界面特征

式中:b_u、b_d分别为顶层和底层接触面基圆直径。
球体在斜碰撞界面处产生一定滑移,相应的虚拟椭圆面积为:
翻浆冒泥病害治理的工程设计、预算与施工,要求提供比较准确的翻浆冒泥病害范围的数据,尤其是翻浆冒泥病害底界里程和深度的数据。翻浆冒泥病害区域的描述如图1所示。

式中:e_u、e_u和e_d、e_d分别为顶层和底层接触面对应椭圆的长轴和短轴尺寸。
滑移面积为椭圆与基圆面积之差的一半,即:

在自行设计的测试平台进行球体自由跌落斜碰撞,如图2所示,利用轴承、支撑块和悬置细线调节平板的倾斜角度以及球体的跌落高度,分别通过钢尺(得力工具有限公司,型号DL8100,精度为1 mm)和角度仪(韦度电子有限公司,测量范围0°~90°,精度为0.02°)进行测量。通过可调电压直流电源(Wanptek,型号KPS605DF,0~60 V,0~5 A)供电,电路中设置开关控制电磁吸铁(伊莱克电气有限公司,型号ELE–P25/20,DC24 V-8 kg),当开关断开,电磁吸铁磁力消失,球体自由跌落,与钢板发生碰撞。在钢板上铺设一张打印纸(210 mm× 150 mm×0.096 mm),并且在其上边覆盖一张薄型复写纸(127 mm×90 mm×0.028 mm),通过千分尺(韦度电子有限公司,0~25 mm,精度为0.001 mm)测量接触面长轴c和短轴c,存在c=b/2+e/2和c=b=e,利用式(1)、(2)和(4)分别计算得到基圆、椭圆和接触面面积,进而获得能量吸收率和转换率。

根据式(4)可得传递到底层的能量比率为:

为了分析球体斜碰撞过程中包装材料(如瓦楞纸板、珍珠棉板、泡沫网袋、气泡膜和橡胶衬垫等)界面处能量参量的变化规律,将直径为30 mm的钢球从高度400 mm处自由跌落到倾斜30°的钢板上,获得不同材料对应的接触形状,见表1。从测试结果来看,由于这些材料内部结构不连续、不一致,如瓦楞的顶端和空隙部分、珍珠棉板的大变形、网袋的连接部位、气泡的破裂等,将导致接触形状及其边缘不规则,从而使测量结果存在很大的不确定性。相比之下,橡胶衬垫能够获得较规则的接触形状。

顶层材料吸收能量后,法向和切向的转换率分别为:


将式(7)和式(8)求和得:

将式(4)带入式(9)可得:

从式(6)和式(10)可以看出,当顶层材料吸收外加能量后,一部分转换为法向压缩和切向运动,另一部分则传递到基底材料,该过程遵循能量守恒定律。
为了分析球体斜碰撞界面能量转换问题,利用接触面积计算外加能量的吸收率和法向、切向上的转换率,通过不同碰撞工况研究能量参量的变化规律。
2 界面能量变化测试方法和试验平台
森林资源作为自然赋予人类重要的资源、作为我国重要的资源之一,是人们赖以生存的天然氧吧,不但能够调节环境气候,而且还蕴含着重要的经济价值,与人们的生产生活密切相关。近些年来,由于人们不合理的开发森林资源、滥砍滥伐现象较为严重,在一定程度上加剧了森林资源的短缺局势,降低了森林的环保功能。基于此情况下,相关部门要加强对森林资源的培育与管护,合理的开发利用森林资源,坚持走可持续发展的战略,守候着人们的天然氧吧。
南川地处重庆南部,辖3个街道、31个乡镇,面积2 602平方公里,人口66.1万人,其中农业人口55.4万人。2011年出栏生猪 61.73万头,禽兔 502万只,肉牛 2.88万头,肉羊 2.72万只,中蜂6.22万群。近年来,南川区畜牧兽医部门强化“免疫、检疫、监测、监管”综合管理措施,确保了无重大动物疫病发生、无肉食品安全事故发生,保障了以生猪为支柱,以南川鸡、金佛山中华蜜蜂、涪陵水牛为特色的南川畜牧产业持续快速发展。南川区连续多年被上级评为兽医工作先进单位,许多创新的管理模式,一直处于全市乃至全国同行业领先水平,并多次代表重庆市接受了农业部领导工作调研和检查。
Gray clustering evaluation of university engineering survey laboratory safety management based on COWA
2.1 球体斜碰撞测试方法
球体碰撞测试方法主要有自由跌落和钟摆试验等,由于球体碰撞后存在回弹运动,为了减小外界因素的影响,文中采用球体自由跌落的方法。将球体悬置于一定高度,常采用手动操作、气动吸盘和电磁吸铁等控制球体释放。手动操作很容易导致球体发生旋转,带来人为误差;气动吸盘需要专门的气源和气路,较为复杂;电磁吸铁具有操作简单、响应速度快等优点,并且测试结果的一致性较好,因此,文中采用直流电磁吸铁进行控制。
关于界面处接触面积的获取方法,目前,主要通过薄膜压力传感器或者材料损伤压痕获得。薄膜传感器很大程度上会改变碰撞接触状态,不适合界面问题的研究;直接测量材料压痕的前提是界面能够产生损伤,而多数斜碰撞不会产生明显压痕或损伤。文中采用在碰撞界面放置一张薄型复写纸的简单方法,既能减少对碰撞材料的影响,又可以获得明显的压痕。
11月22日,京东物流配送机器人智能配送站启用仪式在湖南长沙举行。随着载有用户包裹的配送机器人编队依次发出,全球首个由机器人完成配送任务的智能配送站正式投入使用。首个京东配送机器人智能配送站位于长沙市科技新城,占地面积600平方米,设有自动化分拣区、配送机器人停靠区、充电区、装载区等多个区域,可同时容纳20台配送机器人。当包裹从物流仓储中心运输至配送站后,站内装载人员按照地址将包裹装入配送机器人,再由机器人配送至消费者手中。从配送能力来看,配送站最高设置每天2000个包裹的配送量,能够为周边5公里居民提供物流配送服务。截至目前,京东配送机器人已在全国20余个城市实现落地。
较多的本地流动摊贩选择在游客量较多时在固定的摆摊点做生意而且一般平时生意收入并不太可观,一些店商家在旅客高峰期生意会有所好转,另一些靠近该小镇的学校依靠学生为长期客源生意情况平时才不至于亏损。
2.2 试验测试平台
球体碰撞界面处接触面积为:

图2 球体斜碰撞试验测试装置
3 结果与分析
其余能量则被顶层材料吸收,即:
表1 球体与包装材料斜碰撞接触形状

Tab.1 Contact surface of oblique impact between sphere and packing materials
利用Thornton等[12]提出球体法向碰撞弹性和塑性接触模型,如式(11)所示,分析接触力与接触面积的变化关系。

式中:ic为实测接触力;为有效弹性模量;y、c_y和y分别为屈服状态下对应的接触力、接触半径和接触应力。
IEET工程教育认证不设置任何量化的指标[7-8],主要以学生毕业生具备专业核心能力,并评估毕业后3-5年的专业知识及技能、实务执行与领导统御之基本能力、从事研究之基本能力、培养服务社会之能力。进而进行专业调制和改进,达成具有自己的特色教育目标。其目的让参与认证的专业依照各个专业的定位、行业标准、特色、学生背景及相关环境做出自己专业的学生应该具备的核心能力。并考核学生之学习成果,评量学系、研究所学程是否达到其自设的教育目标[9],及其毕业生是否拥有进入职场应具备之基础专业核心能力。其主要目的是为促进其建立并落实持续改善机制,不断提高工程教育质量。
为了研究球体斜碰撞过程中能量参量的变化规律,以橡胶衬垫为研究对象(500 mm×250 mm,衬垫厚度用表示),使用邵氏硬度计(韦度电子有限公司,型号LXD–A,范围为0~100HA,精度为0.5HA)测量橡胶衬垫的硬度为70HA。对冲击角、衬垫厚度、跌落高度、球体直径及其材料密度等因素进行测试,每种工况重复进行10次,取其平均值进行计算分析。

图3 球体法向碰撞接触模型与测试结果对比
3.1 冲击角的影响
将直径为30 mm的钢球从高度400 mm处自由跌落到不同倾斜角的钢板上,并且在上边分别铺设不同厚度(1、2、3、4、5 mm)的橡胶衬垫,其中,厚度为4 mm衬垫上不同冲击角碰撞产生的接触面及其尺寸见表2。钢球与钢板斜碰撞接触面积、能量吸收率,以及能量比率与冲击角间的变化曲线见图4。
利用加速度传感器(上海澄科,型号CT1002L,最大量程为250)和测试系统(NI,型号USB–6002 DAQ)进行测量,采用直径为20 mm钢球与钢板法向碰撞,其他条件与前文的一致,计算过程中,=210 GPa,y=285 MPa。弹性和塑性模型的计算结果以及测试结果见图3。由于打印纸和复写纸的影响,实测面积比计算结果要大,将弹性、塑性模型的结果分别乘以72和42,实际的碰撞应该是混合弹塑性状态,从测试后钢板上留下的凹痕也可得到这样的结论。因为采用的是同样的基准,所以实际的混合弹塑性状态并不影响能量参量的计算。
图4a为球体斜碰撞接触面基圆、滑移面面积与冲击角间的变化曲线。当冲击角较小时,冲击力的法向分量大于切向分量,滑移面面积远小于基圆面积,滑移特征表现得不明显,文献[2,13,15,16]将该状态定义为黏着。从文中测试结果来看,将该状态定义为黏着并不严谨,滑移面存在,只不过是面积较小而已。随着冲击角增加,冲击力的法向分量逐渐变小,基圆面积减小;而切向分量增加,球体更容易运动,使得滑移面积增加。
图4b为球体碰撞能量吸收率的变化曲线。若钢球与钢板直接碰撞,则界面处的材料将外加能量全部吸收;若在钢板上铺设橡胶衬垫,外加能量一部分被衬垫吸收,另一部分被传递到基底,这与式(6)是一致的,该过程符合能量守恒定律。冲击角对能量吸收率的影响很小,能量吸收率基本恒定。厚度为1 mm的衬垫吸收约78%的能量,吸收率随着厚度增加而变大,4 mm衬垫的吸收率达到最大值,约为88%。衬垫厚度从2 mm增加到4 mm,对应能量吸收的增加率分别为8.29%、2.63%和1.73%,随后出现下降。可见,衬垫厚度存在一个最佳值。
(3)币龄累积。币龄累积是针对初期PoS共识机制的常见攻击方式,不存在于PoW。因为持币时间越长,获得记账权的概率越大。在攻击者拥有足够代币之后,可以通过累积时间来达到控制网络新生成块的目的。在代币足够的情况下,攻击者甚至可以将自身代币分散于多个节点,这一攻击方式可以帮助攻击者多次生成有利块,比如回滚以进行双花攻击。占有代币1%的攻击者可以通过2个月不进行交易来进行攻击。基于同样的理由,PoS可能出现冷启动的问题。
庐山西海的旅游景点众多但是开发较少,许多景点设置重复性高,布局也不太合理。许多旅游景点主要以观光为主,养生旅游开发得较少,许多景区的代表性、感染力、参与度等都比较差。还处于低层次的发展阶段,这样就对庐山西海的旅游资源造成极大浪费。
在碰撞界面处,材料吸收外加能量后,法向和切向方向上能量比率的变化曲线见图4c。当冲击角较小时,能量比率变化很小,主要表现为材料的应变能;随着冲击角增加,法向能量比率下降,而切向的增加,从式(9)可看出,两者之和为碰撞总能量,呈现为此消彼长的关系。对于不同厚度衬垫的法向能量比率,曲线存在一个急剧下降点,衬垫厚度越大,转折点对应的冲击角越小,衬垫厚度为1 mm时,对应的冲击角为60°;衬垫厚度为2 mm和3 mm时,对应的冲击角为50°;衬垫厚度为4 mm和5 mm时,对应的冲击角为40°。换言之,材料越软,界面处出现滑移对应的冲击角越小,这主要是由于较软材料吸收能量是有限的,当碰撞材料法向出现能量饱和时,则转向切向方向发展。
表2 不同冲击角下球体碰撞接触面

Tab.2 Contact surface of sphere at different impact angles
3.2 跌落高度的影响
将直径30 mm钢球从不同高度自由跌落到倾斜角30°的钢板上,为了更清楚地表达界面面积的变化,仅描述无衬垫和衬垫厚度为2、4 mm的结果。由于法向和切向的总能量守恒,所以仅描述切向方向能量比率的变化,见图5。
图5a为碰撞界面基圆和滑移面面积的变化曲线,跌落高度从100 mm升至600 mm,面积基本为线性增加,这与弹性、塑性接触理论是吻合的,无衬垫的基圆面积从6.00 mm2增至9.30 mm2,增加率为55.00%;衬垫厚度为2和4 mm的基圆面积分别增加77.81%和99.14%。虽然滑移面积也增加,但是变化特征没有基圆的明显,并且曲线存在一些波动。

图4 不同冲击角下斜碰撞接触面积和能量参量

图5 不同跌落高度下斜碰撞接触面积和能量参量
图5b为界面处能量吸收率的变化曲线,可以看出,能量吸收率随着跌落高度的增加而略微变大。衬垫厚度为1 mm的吸收率从74.36%增至78.27%;衬垫厚度为4 mm的吸收率从85.85%增至88.96%,存在最大的吸收率。可见,跌落高度对界面能量吸收率的影响并不明显。图5c为切向能量比率的变化曲线,与3.1节的结果相比,跌落高度对切向能量比率影响较小。不同衬垫厚度的能量比率的计算结果基本在1%~8%变化,除了无衬垫和衬垫厚度为3 mm的结果存在较大波动,其他工况的结果随着高度的增加变化均很小。无衬垫和不同衬垫厚度切向能量比率的均值分别为4.97%、2.77%、3.36%、3.86%、5.06%和3.86%,这主要是由于球体碰撞接触面的基圆和滑移面面积是同步变化的。
3.3 球体直径的影响
将不同直径的钢球从高度400 mm处自由跌落到倾斜角为30°的钢板上,接触面积、能量参量的表达方式与3.2节的类似,结果见图6。
图6a为不同直径球体斜碰撞界面处基圆和滑移面面积的变化曲线,其变化规律与跌落高度的类似。当球体直径从20 mm增至45 mm时,衬垫厚度4 mm的变化最为明显,基圆面积从31.10 mm2增至154.10 mm2,增加率为395.50%,而相应的滑移面面积增加率较小。与跌落高度的结果相比,球体直径有着更明显的影响,进行简单对比:以衬垫厚度4 mm为例,当跌落高度从200 mm增至400 mm时,基圆面积增加了30.72%;当球体直径从20 mm增至40 mm时,基圆面积增加了305.47%。从能量角度来看,球体的重力势能h==(π3/6)(、和分别为球体的质量、密度和直径,为跌落高度,为重力加速度),由于能量变化与直径是3次方关系,而与高度是线性关系,所以,对于同等比例的变化,直径比高度的影响更大。
图6b为能量吸收率的变化,随着球体直径的加,吸收率略微变大。不同衬垫厚度的变化规律与前文的分析类似。图6c为切向能量比率的变化,切向能量比率均小于8.5%,并随着球体直径增大而减小。从变化比较明显的无衬垫和衬垫厚度为4 mm的结果来看,球体直径从20 mm增至45 mm时,切向能量比率分别从7.73%减少到4.82%和从8.35%减少到2.17%。可见,随着球体直径增加,碰撞过程中界面材料的应变能增多,而摩擦耗能减少。
3.4 球体材料的影响
将钢、铜和铝等不同材料的球体(直径为20 mm)从高度400 mm处自由跌落到铺设有厚度为2 mm衬垫的钢板上,不同冲击角工况下的结果见图7。
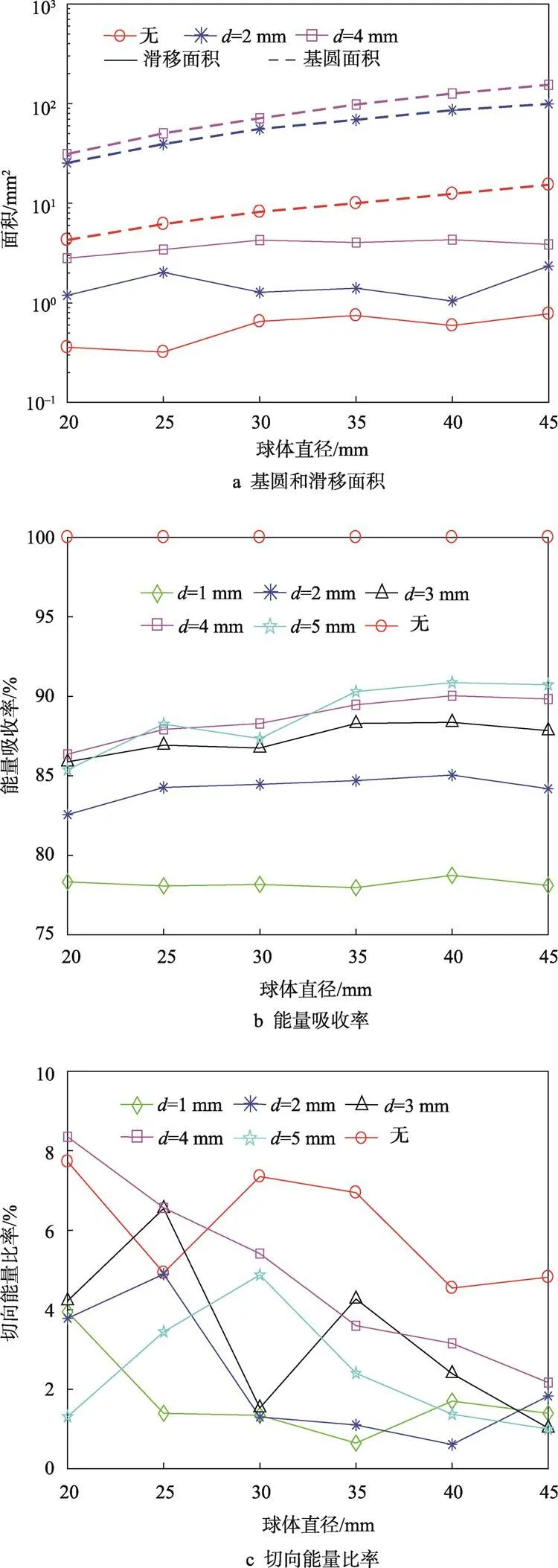
图6 不同球体直径下斜碰撞接触面积和能量参量

图7 不同球体材料下斜碰撞接触面积和能量参量
不同材料球体碰撞接触面基圆和滑移面面积的变化,如图7a所示,与3.1节的分析结果类似。当冲击角小于40°时,对应的基圆面积变化均较小,铜球比钢球的略微大些,而这两者的基圆面积变化明显大于铝球的。这主要是由于材料密度的影响,铜和钢的密度分别为8.96 g/cm³和7.93 g/cm³,大于铝的密度2.70 g/cm³,同等体积,质量较大的球将产生更大的接触面积。当冲击角从40°增至80°时,基圆面积明显下降,铜、钢和铝球基圆面积的下降率分别为64.29%、64.52%和71.38%。铝球的下降率最大,这是因为铝球的密度较小,运动状态更容易改变。滑移面面积的变化与基圆面积的正好相反。
绿色经济发展是一个动态的过程,其效应需要一定的时间才能反映出来。因此,指标的选择要充分考虑到动态变化特点,选取多年数据进行动态分析。
为了便于对比,在图7b和图7c中描述无衬垫碰撞结果。能量吸收率的变化见图7b,铜球和钢球的数值比较接近,在80%~84%内变化,而铝球的要小些,在74%左右变化。切向能量比率的变化见图7c,当冲击角小于60°时,能量比率缓慢增加,3种材料均在8.2%以下,无明显区别。当冲击角大于60°时,切向能量比率急剧增加。当冲击角为80°时,钢、铜和铝球在衬垫厚度2 mm的比率分别为43.32%、40.26%和38.34%,相比之下,同等体积,质量较小的球体的切向能量比率较小。
4 结语
文中基于球体斜碰撞接触面积研究界面处能量吸收率、传递率和转换率,分析了不同因素对这些参量的影响。常见的包装材料结构形式比橡胶的复杂,文中的分析可为其他材料的研究奠定基础,主要结论如下。
1)利用接触面积计算能量吸收率、传递率和转换率,遵循能量守恒定律,具有可行性。
2)随着跌落高度、球体直径和密度增加,接触面积和能量吸收率变大,这与接触理论的分析结果是一致的;衬垫存在最佳吸能厚度,而冲击角对能量吸收率的影响很小。
3)随着冲击角增加、球体直径减小,法向能量比率下降,而切向的比率增加;能量转换曲线存在一个急剧下降点,衬垫厚度越大,转折点对应的冲击角越小;跌落高度和材料密度对能量比率并无明显的影响。
[1] 潘迪, 韩勇, 张坤伦, 等. 液晶电视包装件跌落仿真及结构优化[J]. 包装工程, 2019, 40(11): 94-99.
PAN Di, HAN Yong, ZHANG Kun-lun, et al. Drop Simulation and Structure Optimization of LCD TV Package[J]. Packaging Engineering, 2019, 40(11): 94-99.
[2] DOMÉNECH-CARBÓ A, DOMÉNECH-CASASÚS C. Analysis of Microsphere Oblique Impact with Planar Surfaces Based on the Independent Friction-Restitution Approach[J]. Journal of Aerosol Science, 2020, 140: 1-3.
[3] STROPEK Z, GOACKI K. Bruise Susceptibility and Energy Dissipation Analysis in Pears under Impact Loading Conditions[J]. Postharvest Biology and Technology, 2020, 163: 1-7.
[4] STRONGE W J. Impact Mechanics[M]. Cambridge: Cambridge University Press, 2000: 86-145.
[5] BRAKE M R. An Analytical Elastic Plastic Contact Model with Strain Hardening and Frictional Effects for Normal and Oblique Impacts[J]. International Journal of Solids and Structures, 2015, 62(1): 104-123.
[6] 王庆朋, 张力, 唐志刚, 等. 粗糙结合面法向接触的能量耗散与阻尼特性研究[J]. 振动与冲击, 2017, 36(2): 129-133.
WANG Qing-peng, ZHANG Li, TANG Zhi-gang, et al. Energy Dissipation and Damping Characteristics Analysis on the Normal Contacts of Rough Joint Surfaces[J]. Journal of Vibration and Shock, 2017, 36(2): 129-133.
[7] MESSAADI M, KERMOUCHE G, KAPSA P. Numerical and Experimental Analysis of Dynamic Oblique Impact: Effect of Impact Angle[J]. Wear, 2015, 332-333: 1028-1034.
[8] NISHIDA M, HAYASHI K, TOYA K. Influence of Impact Angle on Size Distribution of Fragments in Hypervelocity Impacts[J]. International Journal of Impact Engineering, 2019, 128: 86-93.
[9] 谢若泽, 钟卫洲, 黄西成, 等. 吸能包装模型结构的冲击响应[J]. 爆炸与冲击, 2019, 39(10): 42-50.
XIE Ruo-ze, ZHONG Wei-zhou, HUANG Xi-cheng, et al. Impact Response of Scaled Models of an Energy-Absorbing Container[J]. Explosion and Shock Waves, 2019, 39(10): 42-50.
[10] KEY C T, ALEXANDER C S. Numerical and Experimental Evaluations of a Glass-Epoxy Composite Material under High Velocity Oblique Impacts[J]. International Journal of Impact Engineering, 2020, 137: 1-10.
[11] MAW N, BARBER J R, FAWCETT J N. The Rebound of Elastic Bodies in Oblique Impact[J]. Mechanics Research Communications, 1977, 4(1): 17-22.
[12] THORNTON C, NING Ze-min. A Theoretical Model for the Stick/Bounce Behaviour of Adhesive, Elastic- Plastic Spheres[J]. Powder Technology, 1998, 99(2): 154-162.
[13] DOMÉNECH-CARBÓ A. Analysis of Rolling Friction Effects on Oblique Rebound by Redefining Tangential Restitution and Friction[J]. Physics of Fluids, 2019, 31(4): 1-9.
[14] 韩维, 胡海岩, 金栋平. 两自由度振动系统的斜碰撞分析[J]. 力学学报, 2003, 35(6): 723-729.
HAN Wei, HU Hai-yan, JIN Dong-ping. Analysis of Oblique Impact of a Vibrating System of Two Degrees of Freedom[J]. Acta Mechanica Sinica, 2003, 35(6): 723-729.
[15] DONG H, MOYS M H. Experimental Study of Oblique Impacts with Initial Spin[J]. Powder Technology, 2006, 161(1): 22-31.
[16] CROSS R. Oblique Impact of a Steel Ball[J]. Powder Technology, 2019, 351: 282-290.
[17] 冯斌, 孙伟, 石林榕, 等. 收获期马铃薯块茎碰撞恢复系数测定与影响因素分析[J]. 农业工程学报, 2017, 33(13): 50-57.
FENG Bin, SUN Wei, SHI Lin-rong, et al. Determination of Restitution Coefficient of Potato Tubers Collision in Harvest and Analysis of Its Influence Factors[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(13): 50-57.
[18] IRELAND P M. Impact Tribocharging of Soft Elastic Spheres[J]. Powder Technology, 2019, 348: 70-79.
Experimental Study on Energy Transfer and Conversion during Sphere Oblique Impact of Packing Materials
WANG Qing-peng1,2, LI Wei1, WANG Heng1, WANG Zhen-feng1,2, LI De-feng1, XU Guang-yin1,2
(1. School of Mechanical and Electrical Engineering, Henan Agricultural University, Zhengzhou 450002, China; 2. Henan Provincial Cold Chain Information and Equipment Laboratory for Logistics of Agricultural Products, Zhengzhou 450002, China)
The work aims to propose a calculation model of energy rate of absorption, transfer and conversion based on the geometrical characteristics of impact contact surface to solve the problems of energy changes of packing materials at interface and their quantitative characterization during sphere oblique impact. Firstly, the geometrical characteristics of contact surface of sphere oblique impact was analyzed, and the computation formula of the absorption rate, transfer rate and energy ratios at different directions was proposed through the areas of base circle and slip surface. Subsequently, the test device of oblique impact of sphere free falling was built. Then, the effects of the impact angle, cushion thickness, drop height, sphere diameter and material density on the energy parameters were analyzed. It was feasible to calculate the energy absorption rate and conversion rate by impact contact area, following the law of conservation of energy. The energy absorption rate was nearly above 75%, becoming greater with increasing drop height, sphere diameter and material density, while the effect of impact angle was slight. The normal rate of energy conversion decreased with the increasing impact angle and the decreasing sphere diameter, but the tangential energy ratio was opposite, and the falling height and density had no obvious effect on the energy ratio. Under given working conditions, the optimum energy absorption thickness of the cushion was 4 mm. This analysis can be conducive to studying the energy change and contact characteristics at the interface of packing materials.
packing materials; oblique impact; contact area; energy absorption; transfer and conversion
O313.4
A
1001-3563(2022)17-0093-09
10.19554/j.cnki.1001-3563.2022.17.012
2021–11–18
中国博士后基金项目(204225);河南省级科技攻关项目(202102110127);河南省高等学校重点科研项目(20B210010);河南农业大学科研启动项目(30500461)
王庆朋(1987—),男,博士,讲师、硕导,主要研究方向为农产品物流测试技术。
责任编辑:曾钰婵
