基于改进模糊控制算法的分数阶控制器设计
2022-09-21李莉陈晓静徐智超
李莉,陈晓静,徐智超
(大连科技学院电气工程学院,辽宁大连116052)
0 前言
在控制领域中,线性最佳控制的分数阶控制器在各个行业应用广泛,其设计可按照被控制对象模型展开,操作简捷,实用性强。目前,分数阶控制器种类繁多,如余艳伟和徐鹏飞设计的基于内模控制的分数阶控制器,该控制器参数按照最高灵敏度数值设定,选择参数具有盲目性,其控制准确度较差;魏立新等设计了基于粒子群算法的液压APC系统分数阶PID控制器,该控制器主要应用在高冷液压系统,应用范围小,并且使用粒子群算法,迭代次数多,运算用时长,导致控制效果较差。针对目前控制器存在的一系列问题,本文作者基于改进模糊控制算法设计分数阶控制器,采用区间二型模糊逻辑系统结构与改进的径向基函数(Radial Basis Function,RBF)模糊神经网络算法实现控制。区间二型模糊逻辑系统可对数据集合解模糊化,实现降阶处理。改进的RBF模糊神经网络算法可将前件网络由三层增加至四层,具有减少模糊规则层节点数量、降低冗余模糊规则、提升学习速度等优势。使用区间二型模糊逻辑系统结构与改进的RBF模糊神经网络算法,可实现控制器多方面需求,实际应用意义较大。
1 改进模糊控制算法的分数阶控制器设计
1.1 区间二型模糊逻辑系统结构
与一型模糊逻辑系统相比,二型模糊逻辑系统具备降阶流程,可将二型模糊集合转化为一型模糊集合,对该集合实施解模糊化,实现二型模糊逻辑系统的降阶。图1所示为二型模糊逻辑系统结构。

图1 二型模糊逻辑系统结构
根据图1所示的二型模糊逻辑系统结构,利用KM(Krasnoselskii-Mann)降阶算法对区间二型模糊集合进行降阶处理。假设实数区间[,],则、端点可由以下公式表示:
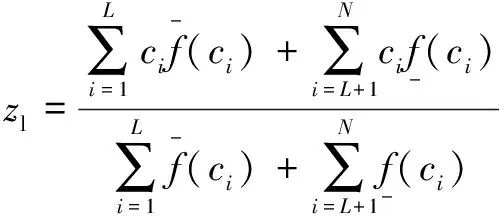
(1)

(2)
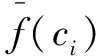
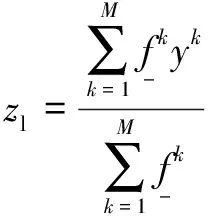
(3)
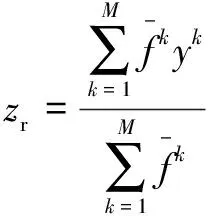
(4)
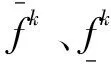
降阶后的区间二型模糊集合为
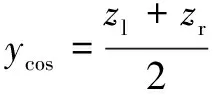
(5)
1.2 分数阶区间二型模糊逻辑系统
根据公式(5)得到的降阶后的区间二型模糊集合,利用分数阶算子构建分数阶区间二型模糊逻辑系统。Riemann-Liouville可定义分数阶微积分,由公式(6)表示:
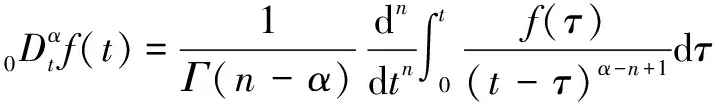
(6)
其中:(·)为伽马函数;为整数,≥>-1。
用Grunwald-Letnikov定义分数阶微积分流程如下:

(7)
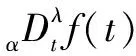
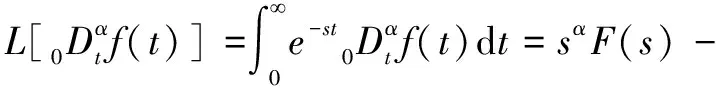

(8)
其中:-为收敛因子。
设置初值为0,则有:
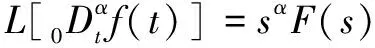
(9)
分数阶PID控制器时域可由公式(10)计算:

(10)
其中:()为时域函数输出量;()为时域函数输入量;为比例增益;为积分增益;为微分增益;分数阶PID的传递函数经过拉普拉斯转换可由公式(11)表示:
()=++
(11)
其中:>0,>0。
1.3 改进的RBF模糊神经网络结构与算法
在设计区间二型模糊逻辑系统的基础上,为避免模糊规则层节点数量较多导致其控制精度和控制灵敏度较低的问题,使用改进的RBF模糊神经网络算法对其进行优化设计。具体过程:将RBF模糊神经网络的前件网络由三层变更为四层,后件网络中使用权值的二阶学习,以减少模糊规则层节点数量,提升权值作用。改进后的RBF模糊神经网结构如图2所示。

图2 改进后的RBF模糊神经网结构
根据图2所示的改进后的RBF模糊神经网络结构,分别从前件网络、后件网络、修正参数3个方面优化分数阶控制器。
1.3.1 前件网络
(1)输入层。用连接输入层每个结点之间和输入向量的分量,可传输输入值=[,,…,]至下一层,输入变量数量即为结点数量=。

(12)
其中:=1,2,…,。
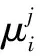
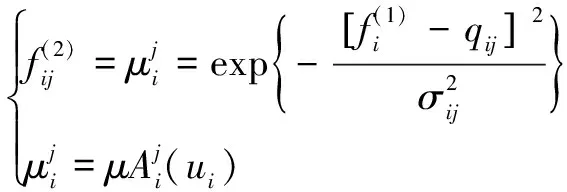
(13)

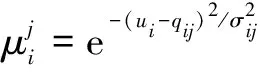
(14)
其中:表示隶属函数中心;表示隶属函数宽度,其结点总数为

(15)
(3)模糊推理层可计算各个规则的适合度,一个模糊规则表示一个结点,可用该规则匹配模糊规则前件,其公式如下:
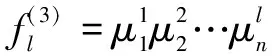
(16)
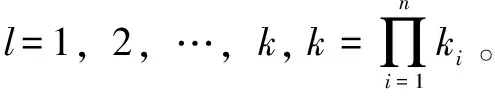
1.3.2 后件网络
(1)输入层可将输入变量传输至第二层,其公式为
=
(17)
(2)中间层通过计算任一规则后件,在个结点中,每条规则都由一个结点表示,则有:
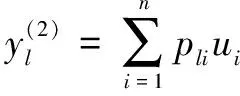
(18)
其中:=1,2,…,。
(3)输出层可计算二型模糊逻辑系统的输出,其公式为

(19)
1.3.3 修正参数
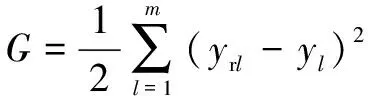
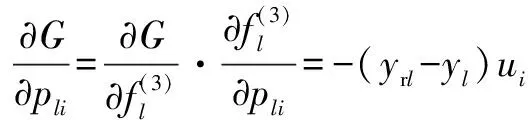
(20)
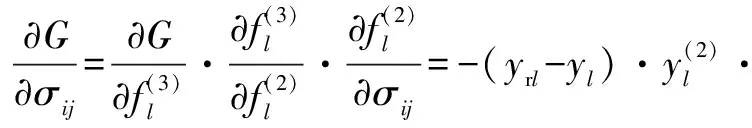
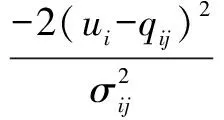
(21)
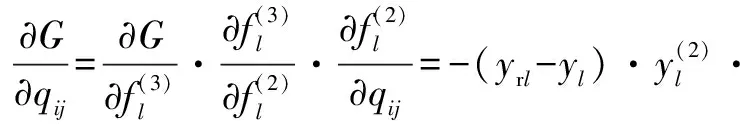
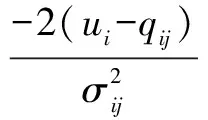
(22)

(23)

(24)
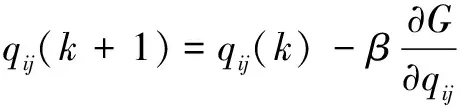
(25)
其中:=1,2,…,;=1,2,…,;=1,2,…,;表示学习率,>0。
为进一步提升控制器的灵敏度,将权值的平方运用于后件网络多项式运算中,则:

(26)
其中:=1,2,…,。
那么修正后的如下:
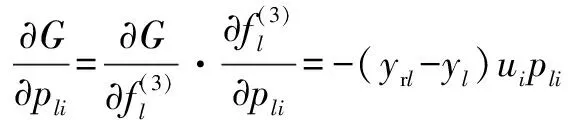
(27)
至此,实现基于改进RBF模糊神经网络算法的分数阶控制器设计。
2 实验分析
为验证所设计的控制器的控制效果,选取文献[4]设计的基于内模控制的分数阶控制器、文献[5]设计的基于粒子群算法的液压APC系统分数阶PID控制器为对比控制器,利用MATLAB软件分别建立3种控制器的仿真环境,并设置温度为26 ℃,控制误差±0.5 ℃。分别使用3种控制器对温度进行控制,其阶跃响应曲线如图3所示。
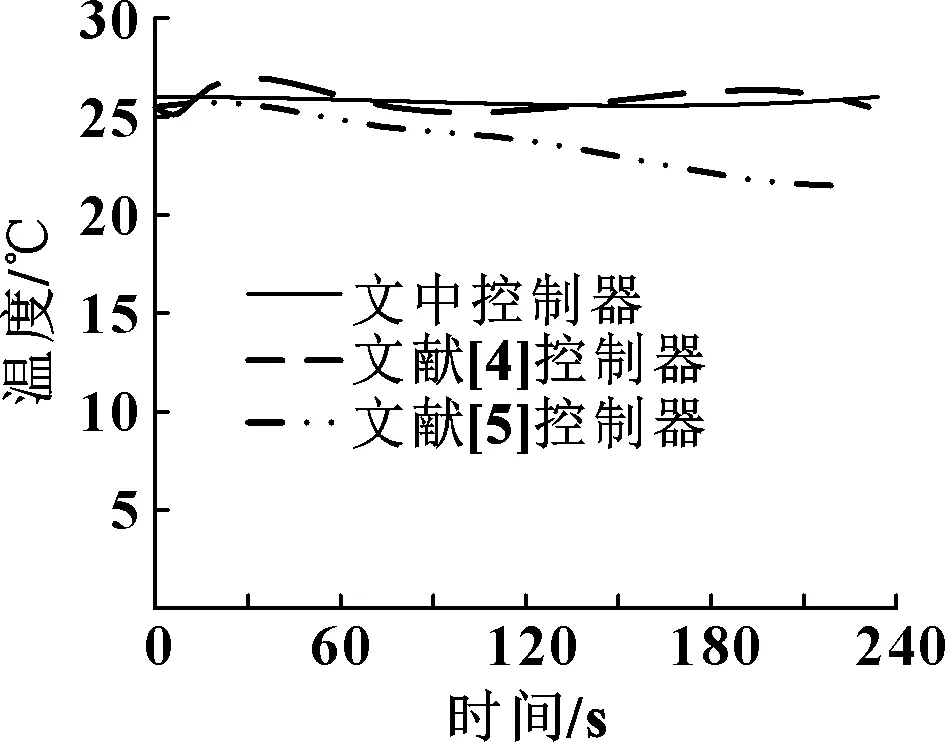
图3 3种控制器阶跃响应曲线
由图3可知:文中控制器阶跃响应曲线较平滑,可稳定控制温度在26.01 ℃左右,与所控温度目标相差仅为0.01 ℃,原因是本文作者在设计控制器过程中选择恰当的切换点数值作为左右两端端点值,利用简化降阶算法减少寻找切换点迭代次数,提高了控制的稳定性;而文献[4]控制器曲线为波浪状,控制温度时高时低,控制稳定性较差;文献[5]控制曲线呈现下降趋势,在=30 s时,温度较准确,当时间超过30 s后,温度明显低于设置温度,温度控制不稳定。
控制器性能的优良可由其控制指标呈现,其指标包括超调量、余差、调节时间等。对比3种控制器控制指标,结果如表1所示。
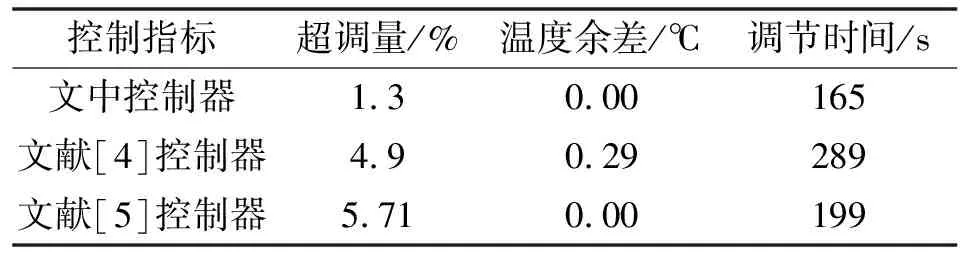
表1 控制指标对比
由表1可知:文中控制器超调量最小,为1.3%,其温度余差与文献[5]的余差都为0,但文中控制器超调量与调节时间都较小。由此可知,文中控制器用时短、偏差小、控制能力强。
对比3种控制器不同时间的温度控制相对偏差情况,结果由图4所示。可知:当=0~3.8 s时,文中控制器控制的温度偏差高于文献[4]与文献[5]控制器的温度偏差;当>3.8 s后,文中控制器控制的温度偏差小于文献[4]与文献[5]控制器所控制的温度偏差,文中控制器温度偏差为-0.1~0.4 ℃,文献[4]控制器温度偏差为-0.17~0.82 ℃,文献[5]控制器温度偏差为-0.18~0.78 ℃,可见文中控制器控制温度偏差较小,控制器响应性高。
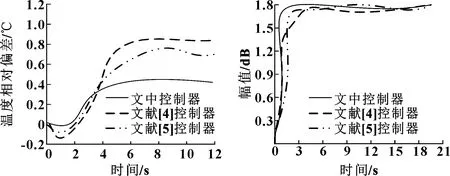
图4 温度控制相对偏差曲线 图5 3种控制器鲁棒性能曲线
为验证所设计的控制器鲁棒性,统计3个控制器控制下不同时间的幅值,结果如图5所示。可知:随着时间的增加,3种控制器幅值主要呈上升趋势,但文中控制器幅值上升速度最快,且达到最高幅值后始终处于稳定状态,文献[4]、文献[5]控制器幅值上升速度小于文中控制器,且波动显著。由此可知,文中控制器控制稳定性好、鲁棒性强。
控制器灵敏度与互补灵敏度影响该控制器整体性能,3种控制器灵敏度与互补灵敏度曲线由图6所示。

图6 3种控制器灵敏度与互补灵敏度曲线
由图6可知:控制器的灵敏度随着频率的增加而增加;当频率为1×10~1 rad/s时,3种控制器灵敏度均明显上升,文中控制器灵敏度上升幅度明显高于文献[4]与文献[5]控制器;当频率为1~1×10rad/s时,文中控制器灵敏度保持0不变,而文献[4]与文献[5]控制器灵敏度均低于文中控制器灵敏度;控制器的互补灵敏度随着频率的增加而降低;当频率为1×10~1 rad/s时,文中控制器互补灵敏度保持0不变,并且高于文献[4]与文献[5]控制器互补灵敏度;当频率为1~1×10rad/s时,3种控制器互补灵敏度呈下降趋势。因此,文中控制器灵敏度高于对比系统灵敏度,实际使用性能较强。
为进一步验证所设计的控制器的实际使用性能,分别对比3种控制器的时域响应情况,结果如图7所示。
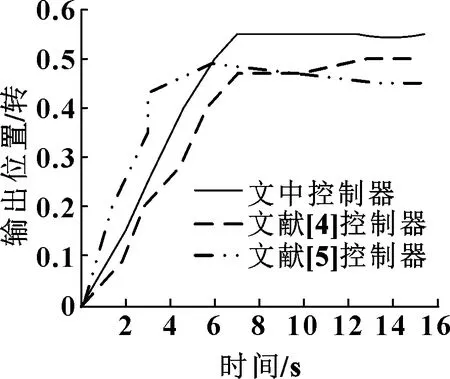
图7 3种控制器时域响应曲线
由图7可知:控制器输出位置随着时间的增加而增加,当到达一定时间后,输出位置上下浮动较小;文献[5]控制器时域响应曲线在=4.7 s之前,输出位置高于文中系统与文献[4]控制器,当>4.7 s后,其时域响应曲线呈下降趋势,可见其时域响应性能差,参数跟踪能力低;文献[4]控制器整体输出位置均低于文中控制器与文献[5]控制器,时域响应能力低;而文中控制器时域曲线上升速度快,当时间约大于6.3 s时,其输出位置远高于文献[4]与文献[5]控制器,时域响应与参数跟踪能力较好。
3 结论
本文作者采用分数阶区间二型模糊逻辑系统和改进的RBF模糊神经网络算法设计分数阶控制器。经过实验验证,该控制器控制温度精确度较高,可达到设定控制需求;较对比控制器,其灵敏度与互补灵敏度高、鲁棒性能强、响应速率高。该控制器在实际应用中具有较高的控制效果,可进一步改进,以达到更好的控制效果。
