具有符号式位置正解的2T1R并联机构的运动学分析与尺度综合

2022-09-21陈亚彭红梅刘艳梨吴洪涛

机床与液压 2022年17期

陈亚,彭红梅,刘艳梨,吴洪涛

(1.江苏安全技术职业学院机械工程系，江苏徐州 221011；2.南京航空航天大学机电学院,江苏南京 210016)

0 前言

少自由度并联机构因具有结构、控制简单,制造成本低,精度高等优点而备受学者关注。其中研究较多的是三维纯平移和三维纯转动并联机构，对二维移动一维转动(2T1R)空间并联机构的研究较少。2T1R空间并联机构可通过调整姿态角快速地完成拾取物品操作，具有很好的运动灵活性。2T1R空间并联机构在医疗器械、物料分拣等应用领域具有较好的应用前景。

关于2T1R并联机构的研究，吉昊等人提出一种可应用于脚踝按摩仪领域的2T1R并联机构，根据计算得到的方位特征集、自由度、耦合度验证运动特性，通过序单开链的运动学建模方法计算得到位置正解和逆解的解析式，仿真分析其工作空间和转动能力、奇异性等特性。沈惠平等针对并联机构误差分析、动力学分析、运动轨迹规划分析复杂的问题，提出2种具有解析式位置正解且运动解耦的2T1R并联机构，分别对这2种机构建模进行运动学和性能分析，对比分析优选出最佳性能的机型。张彦斌等设计了一种弱耦合空间三自由度并联机构,采用方位特征集分析机构的运动特性，同时建立机构的正逆解方程，在此基础上分析机构的奇异性，并分类分析研究。邓嘉鸣等基于方位特征方程的并联机构设计理论与方法，提出一种无寄生运动非对称空间2T1R并联机构，对机构的拓扑特性进行了分析，基于序单开链法的运动学原理得到机构正逆解，同时研究了机构的工作空间、奇异位形、转动能力等工作性能。黄勇刚和黄茂林根据螺旋理论与集合论原理,基于动平台所受约束与支链约束之间的关系,分析平面机构无过约束构型条件，综合出一批无过约束平面2T1R并联机构。张彦斌等设计一种完全各向同性的三自由度空间并联机构，通过调整支链的排列关系，演化出另外2种新型整周旋转(360)的2T1R并联机构，最后根据螺旋理论完成自由度分析以及求解出机构的运动学正逆解。刘伟和刘宏昭基于位移流形理论，综合出具有2T1R与2R1T2种运动模式的并联机构，通过螺旋理论研究不同运动模式下的自由度特征。邹建星等设计一种两平移一转动(2TIR)并联机构，对机构的拓扑性能进行分析，证明机构的运动性质，建立运动学方程推导得到位置逆解解析式，分析工作空间和转动能力等性能指标。

本文作者利用方位特征方程(Position and Orientation Characteristics，POC)的并联机构设计理论与方法，提出一种具有解析式位置正解且部分运动解耦的2T1R并联机构。分析机构的主要拓扑特性,由于耦合度为零，推导出运动位置正解与逆解的解析式；研究了机构的工作空间形状和大小及奇异性存在条件；以给定的工作空间指标作为优化目标函数的约束条件，建立工作空间最小化的优化目标函数，优化得到一组最佳参数解，为后期的轨迹规划、动力学分析奠定理论基础。

1 并联机构设计与拓扑结构分析

1.1 机构设计及坐标系的建立

如图1所示为2T1R机构结构简图,支链1由1个平面五杆闭回路和1个转动副串联而成，、、轴线相互平行且垂直于，移动副、的移动方向一致，轴线与平行。支链2由一个平行四边形机构和一个副、转动副构成，其中，副与副互相平行。副的移动方向和移动副一致。图2所示为2T1R并联机构三维模型。

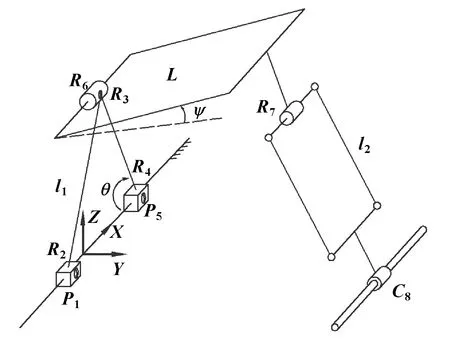
图1 2T1R并联机构结构简图

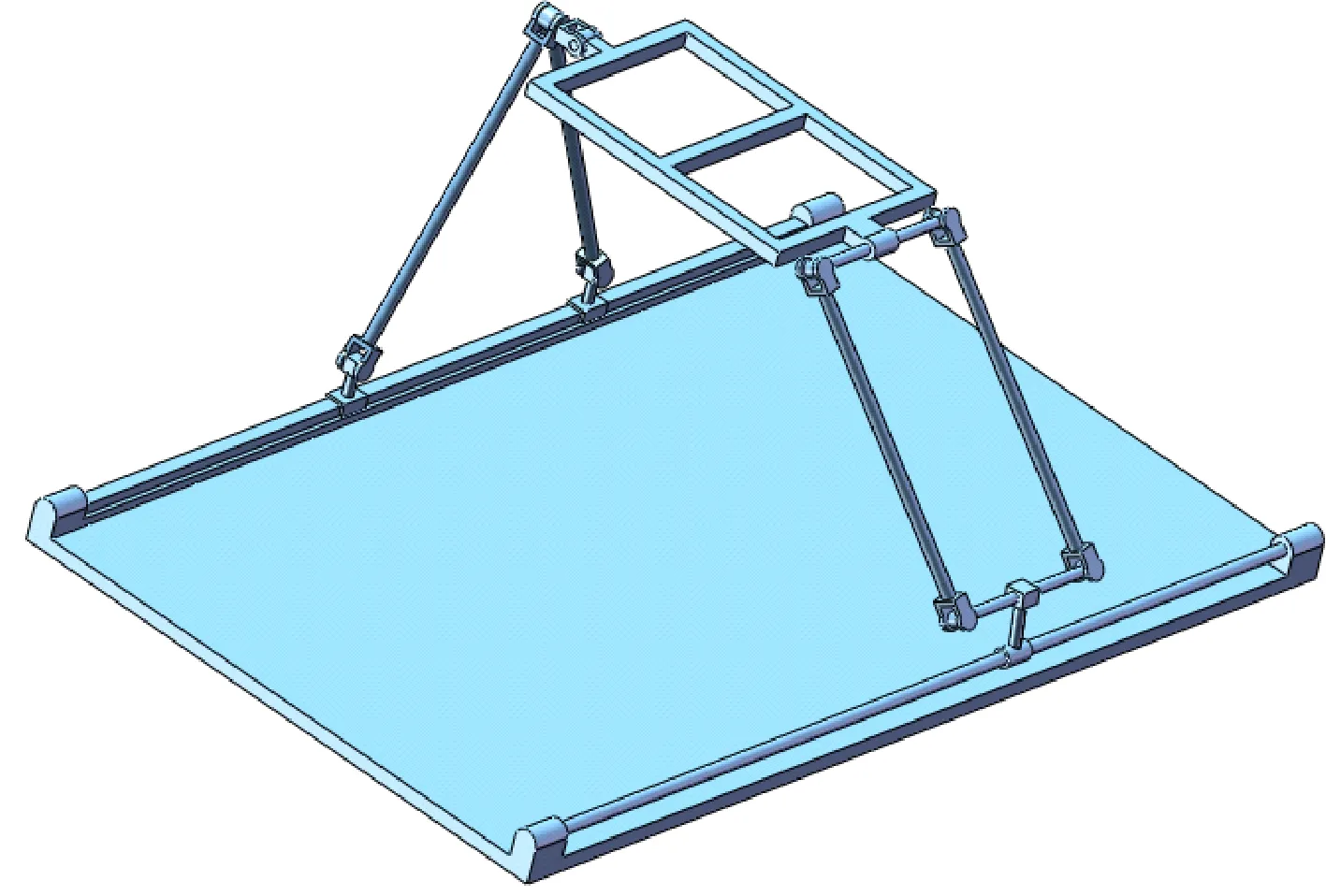
图2 2T1R并联机构三维模型

在静平台上建立坐标系{-}，其中轴与移动副所安装的边平行，与移动方向垂直。轴垂直于静平台，该机构以主动移动副的位置作为独立的输入参数，用(,,)表示，输出参数为(,,)，即动平台的位姿，具体参数如表1所示。

表1 参数描述

1.2 机构动平台POC分析

并联机构拓扑结构特性分析方法见文献[13]，具体计算过程如下：

(1)首先选定动平台上任意一点，作为动平台上基准点。

(2)其次，需要得到每条支路的POC集，其中机构存在3条支路，第一条支路的POC集为

(1)

其中:，且移动副，移动方向与转动副垂直。因此，

(2)

同理，第2条支路的POC集为

(3)

第3条支路的POC集为

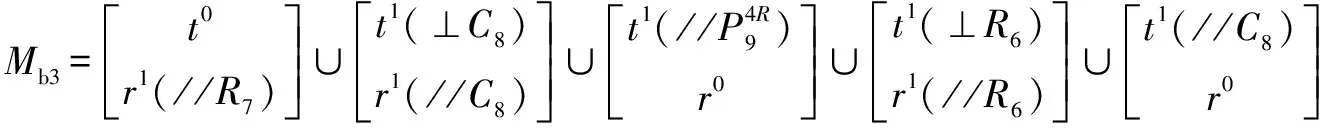
(4)

其中，副可以衍生成副和副，因此，

(5)

(3)建立方位特征方程可得：

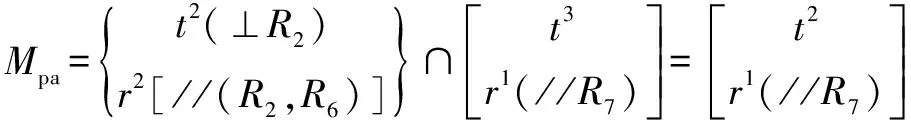
(6)

(4)需要得到每一条回路独立位移方程数，该机构存在2条回路，确定第一个独立回路的独立位移方程数,由下式可得：

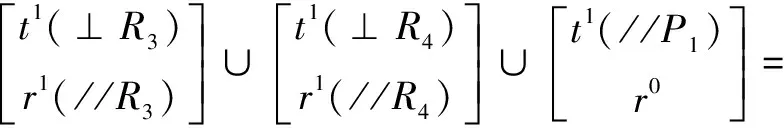
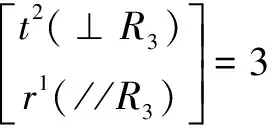
(7)

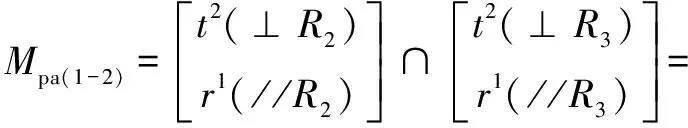
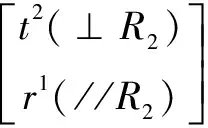
(8)

(5)确定第2个独立回路的独立位移方程数。

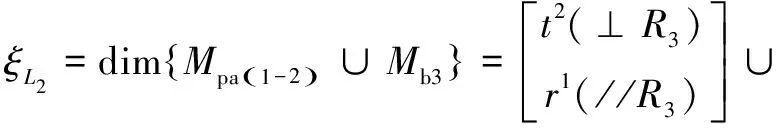
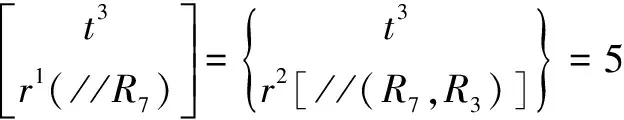
(9)

(6)确定机构的方位特征集。

(10)

(7)计算自由度，过程如下：

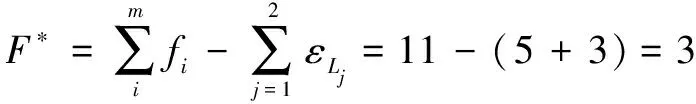
(11)

(8)根据上面的分析过程，=3，=5，计算约束度可得：

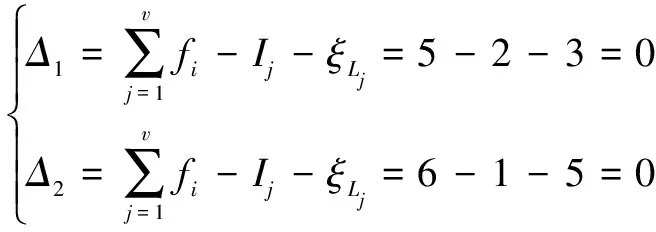
(12)

(9)基本运动链的耦合度计算如下：

(13)

综上所述，计算得到运动链的耦合度为0，说明机构的运动学比较简单，且机构的正解存在解析式，运动学与动力学可单独求解，有利于机构的控制轨迹规划。

2 机构的位置分析

2.1 机构位置正解分析

机构位置正解是指已知输入位移(,,),得到机构动平台的位置姿态(,,)。设置作为动平台参考点，由于△为等腰三角形，根据结构参数和运动副分布，可得以下特征参数方程：

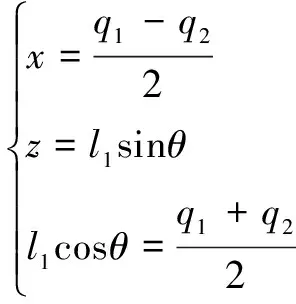
(14)

式(14)联立得到的表达式：

(15)

根据坐标可得到在轴上的坐标：

=+sin

(16)

由于平行四边行机构的杆长不变，存在以下等式关系：

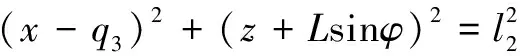
(17)

因此，分离变量可得到参数的表达式

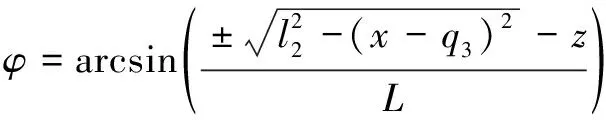
(18)

根据式(15)、式(18)即可解出姿态角参数和各2个,机构正解表达式简单，机构的正解有4组。

2.2 机构位置逆解分析

位置逆解分析是指已知机构的结构参数和末端执行器的位姿，求解主动关节的位置，即已知(,,)，求解(,,)。根据上述正解分析过程等式(14)，可以得到机构的、逆解表达式：

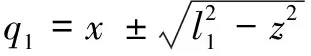
(19)

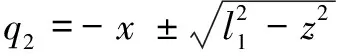
(20)

通过等式(17)可推导出机构主动关节位置的表达式：

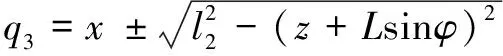
(21)

以上主动移动副机构存在4组位置逆解。

2.3 正逆解验证

给定一组机构参数验证运动学位置分析的准确性，选择参数=0.5 m、=1 m、=1.5 m,根据MATLAB计算得到位置正解数值(见表2);根据公式(19)—式(21)，随机代入数值得到机构位置逆解数值,结果如表3所示。

表2 机构的位置正解数值

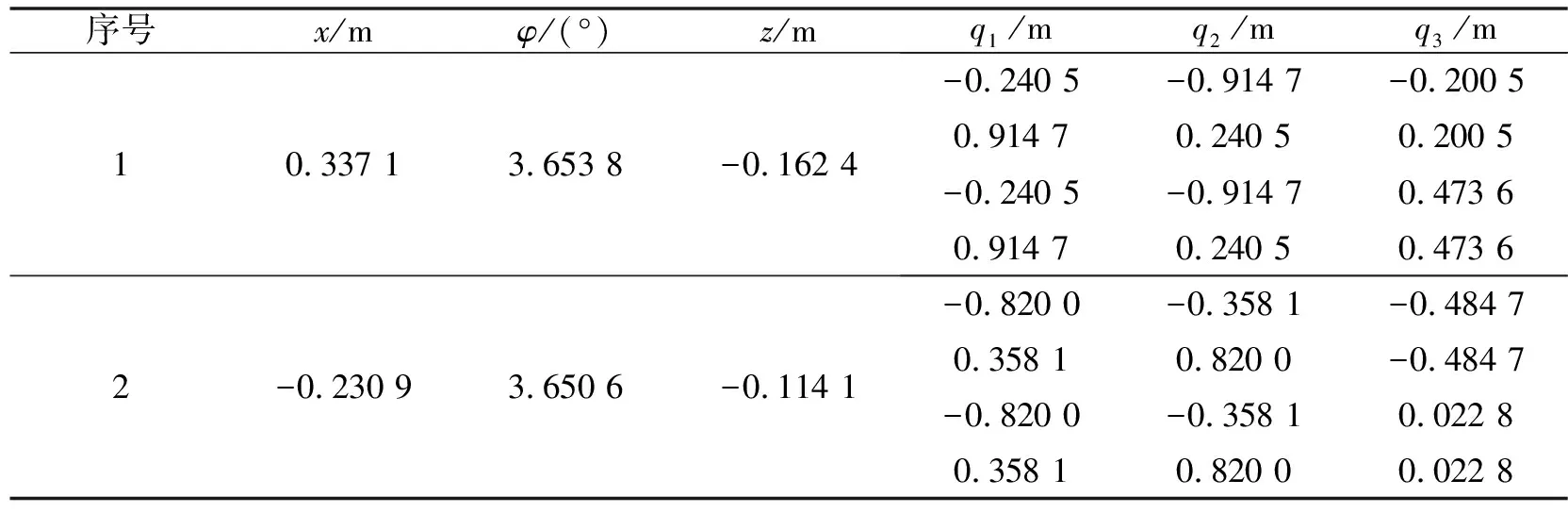
表3 机构的位置逆解数值

根据表2、表3中的数值解可以发现：位置正逆解能够相互对应，验证了分析得到的位置正逆解的可靠性。

3 奇异分析

3.1 机构雅克比矩阵

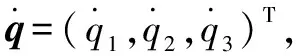
(22)

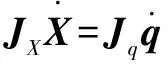
(23)

其中:为逆雅克比矩阵;为正雅克比矩阵。

若非奇异，则

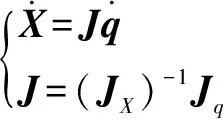
(24)

若非奇异，则

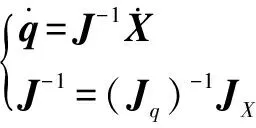
(25)

3.2 逆解奇异性分析

机构逆解奇异存在条件为det()=0且det()≠0，整理可得：det()=2(+)(-)，使得det()=0的条件是=-或=。

因此，存在以下2种情况：

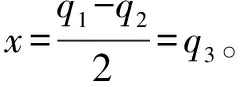
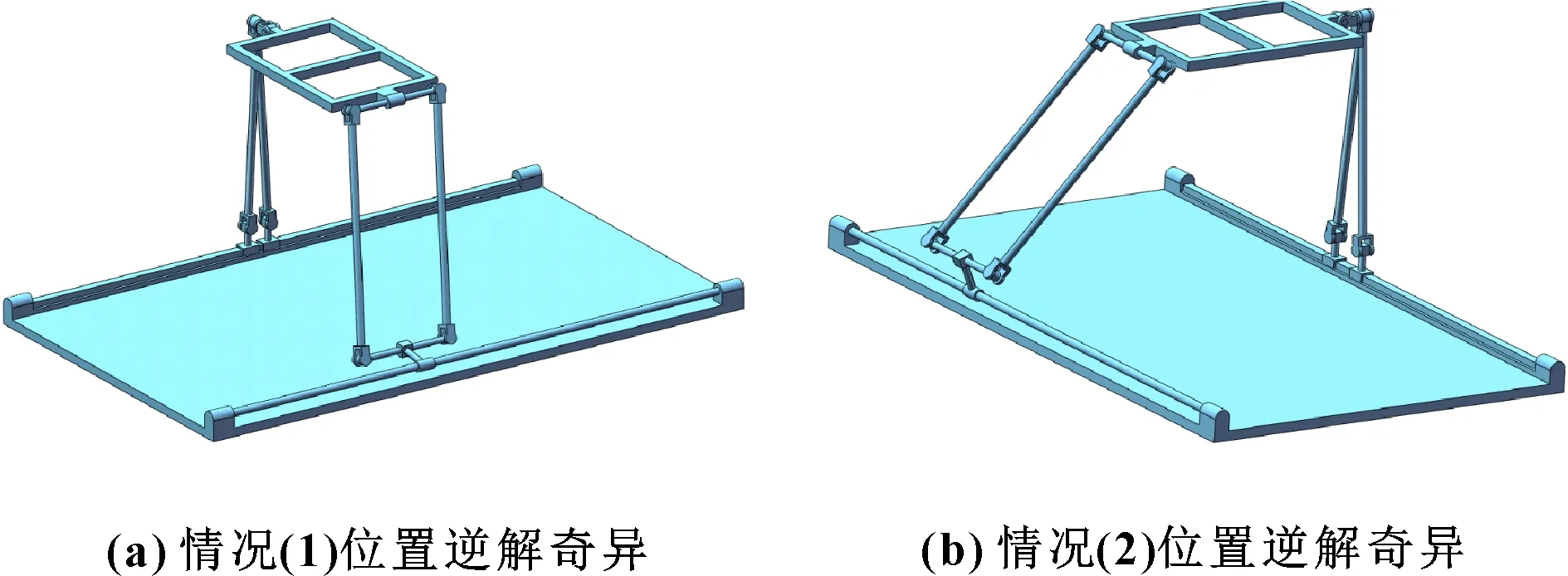
图3 位置逆解奇异

3.3 正解奇异性分析

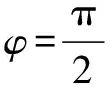
正解奇异情况具体如下：

图4 位置正解奇异

4 机构的工作空间分析

并联机构的工作空间是指动平台参考点所能够达到的位置集合。针对工作空间采用极坐标搜索法实现工作空间图形化分析。判断是否是工作空间内点的条件是所有输入位移(,,)是否满足取值范围要求，是则为工作空间内的点。以下图形化分析均根据表4中的尺寸参数进行求解。

表4 机构的尺寸参数

由图5可知：搜索得到的工作空间图形状为对称的规则形状，呈现对称腰状图，工作空间边界光滑饱满、无空洞情况。

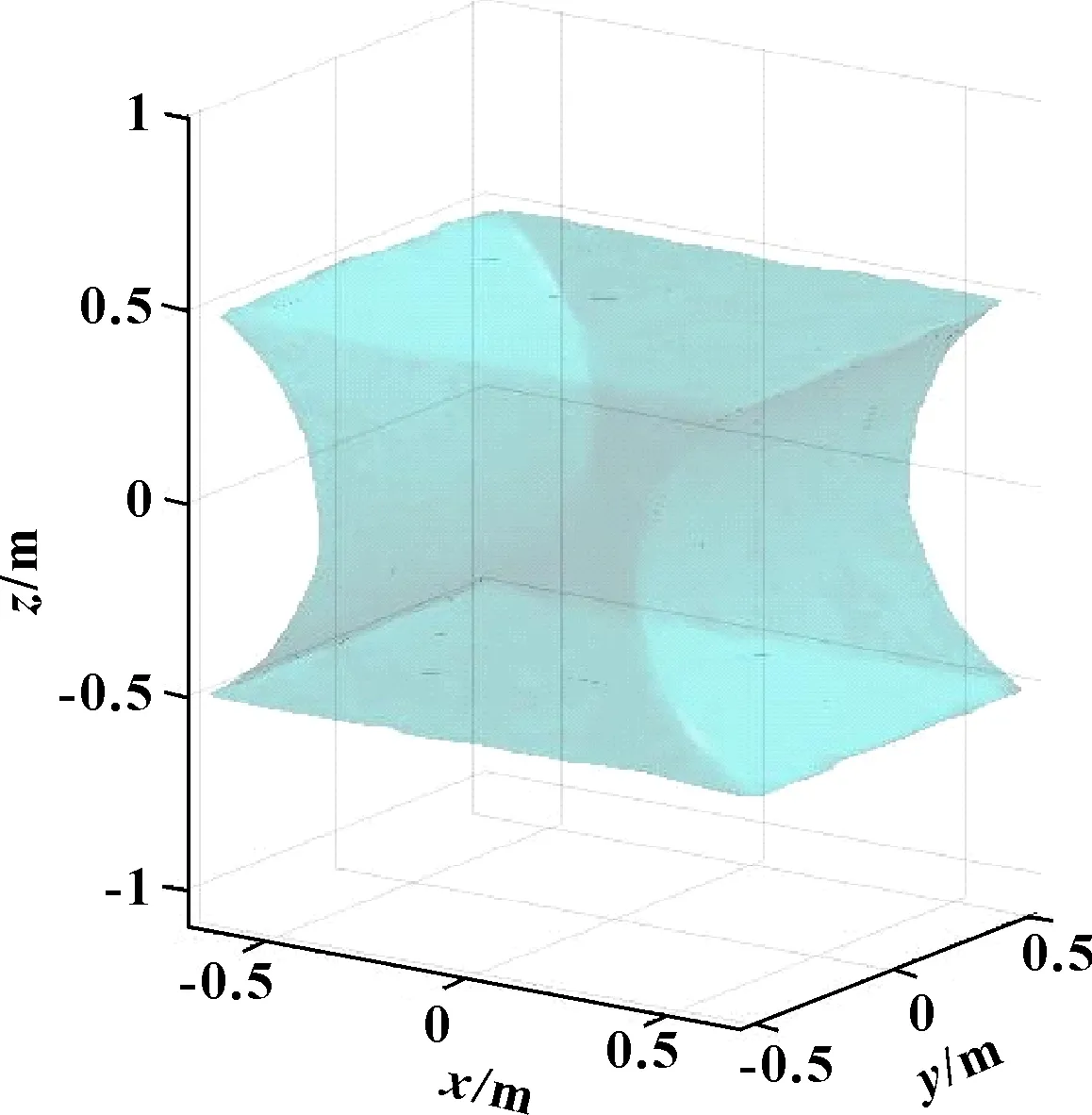
图5 2T1R并联机构工作空间

5 结构参数对工作空间的影响

参数大小选择会直接影响到工作空间的大小。作为并联机构重要性能指标，研究结构参数和工作空间大小的影响关系可用于指导并联机构的应用设计。、、、对工作空间大小的影响关系如图6所示。

图6 参数对工作空间大小的影响关系

分析图6可知：各参数对并联机构工作空间的大小影响显著，其中结构参数对工作空间影响呈线性相关，随着的增加工作空间反而减少；参数对工作空间影响呈先增加后减小的趋势，当∈[0.4,0.6]m，越大，工作空间体积越大，当∈[0.6,1]m，越大，工作空间越小；参数对工作空间大小的影响趋势和参数基本一致，∈[0.5,0.8]m，越大，工作空间体积越大，∈[0.8,1.1]m，越大，工作空间体积越小；而参数增加有利于提高工作空间体积，随着参数增加，工作空间体积越大。

6 机构给定工作空间优化

在某种工况下需要满足特定的工作空间，即给定工作空间区域，尺寸参数越大，越有利于工作空间的增加，但是并非越大越好，因此，需要优化得到的是并联机构工作空间且能包含给定工作空间的同时所对应的并联机构的最优尺寸参数值最小。

6.1 优化模型的建立

给定一个工作空间形状的操作区域，以原点为中心，给定正方体边长为1 m，优化目标为所求工作空间体积最小，约束条件为工作空间包含此正方体。建立此优化目标的目标函数，是要找到合适的约束条件，在约束条件下，采用优化算法获得最小的优化结果。

优化目标为包含此正方体，且可达工作空间体积最小。假定从原点出发，均匀发射出射线，射线集合为{},穿过的给定正方体集合为{}，在某一组参数下，工作空间的边界和射线的交点集合为{}，当≥时，则为满足包含要求。在满足此约束的条件下，目标函数值等于根据蒙特卡罗法计算出这组参数的工作空间体积，若不满足则取一个较大的数作为该组参数的目标函数值。

(26)

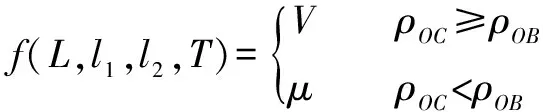
(27)

其中：为一较大的正数，设定为比目标函数值最大值大得多的数，取=100。

6.2 优化算法的选择与优化结果

参数优化算法有很多，选择天牛群优化(Beetle Swarm Optimization，BSO)算法进行目标函数的优化。天牛群优化算法是2017年发表的天牛须搜索算法的改进算法，是一种生物启发式算法。表5列出了相应的算法参数。

表5 天牛群算法参数

经过迭代计算优化得到BSO算法最优参数值如表6所示，目标函数优化过程如图7和图8所示,优化在约80步时完成了迭代过程。

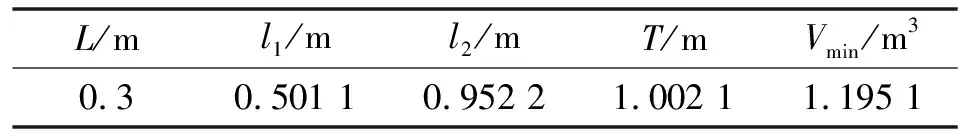
表6 天牛群优化算法结果

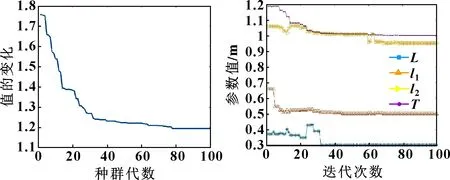
图7 天牛群算法优化过程图8 变量随代数变化影响曲线

图9是相对应的优化工作空间图，绿色为给定工作空间，红色为优化参数下的可达工作空间(呈现为左右凹型的对称空间)。由图9可知:=±0.5 m的平面，=±0.5 m平面和给定工作空间完全重合，而可达工作空间在=±0.5 m和给定工作空间相切，故而目标优化完成，给定工作空间全部包含于可达工作空间，且呈现6个面全部重合的结果，得到了满足给定的工作空间且使并联机构的结构尺寸最小的最优解。