基于改进鸽群算法与领航跟随法的无人车编队方法

支奕琛，谷玉海，龙伊娜，徐小力

(1.北京信息科技大学现代测控技术教育部重点实验室，北京 100192；2.北京信息科技大学机电工程学院，北京 100192)

0 前言

由于单个无人车在自主建图、自主导航等方面的能力有限，很难独自完成如协作运输、集群勘探等工作任务，所以近年来多无人车系统协同工作成为行业研究的热点。无人技术范畴中多无人车协同编队发挥的作用非常关键，如协同反恐、侦查和联合搜救等，因此多无人车系统编队成为关键的课题。对于多无人车系统编队来说，无人车在执行任务的过程中需要实现自主协同并形成编队队形，同时保持队形向目标点行进。结合任务具体要求，队形可以是直线、正方形或者三角形等多种。

路径规划是指在有障碍物的环境下向机器人提供从起点到终点途中的道路信息并规划出一条较优路径。对于移动机器人，规划出一条良好的路径与在路径上成功避障十分重要，不合适的路径可能会导致与其他物体碰撞致使机器人损坏或浪费大量时间。Voronoi图法、遗传算法、蚁群算法、粒子群算法等都是应用较为广泛的路径规划算法，具有很强的代表性。康冰等人设计禁忌栅格，对蚂蚁的线路进行引导、控制，并结合时空数据及时更新调整，获得了全新的蚁群算法。

结合当前文献资料，控制多无人车编队是以虚拟结构法(Virtual-Structure)、基于行为的方法(Behavior-based)、领航-跟随型法、基于路径跟踪的方法、人工势场法、图论法等为主。领航-跟随型编队控制方法的优势在于分析难度小，并且更加精准，在多无人车编队控制中适用性较强。领航-跟随型编队控制法中，通常领航者可以是一个，也可以是多个，除此以外都属于跟随者。在编队的过程中，领航者负责选择最优路径向目标点前进，并在前进过程实时避障，而跟随者利用领航者当前的信息调整各自的状态，实现与领航者保持一定的距离和角度，从而达到编队效果。

文中编队是利用改进鸽群算法与领航跟随法融合实现的。对鸽群算法进行改进，在鸽群算法的前期设置初始解使其初始化，能够提升算法的效率。另外，在算法的地磁算子中加入相应的权重指标，提升算法在整体路径中的规划效率。通过MATLAB进行仿真，结果表明：与PSO算法、量子粒子群优化(Quantum Particle Swarm Optimization,QPSO)算法相比，改进的鸽群算法规划的路径及算法运行时间比其他算法更短，验证了改进鸽群算法的优越性。路径规划完成后，通过领航跟随方法控制无人车编队，以领航者无人车位置与编队队形为依据，完成所有虚拟机器人位置信息的计算；控制所有跟随者无人车向虚拟机器人运动，使队形得以实现。

1 鸽群算法

1.1 鸽群行为说明

鸽子是一种十分常见的鸟，世界各地都在广泛饲养。古时候在没有手机等智能通信设备的情况下，人们都采用鸽子进行远程书信交流，鸽子的记忆能力可见一斑。此外，它还是一种依赖习惯的动物，很多鸽子都可以利用一些建筑物或者标记点进行飞行，甚至还可以结合磁场信息、太阳的运动等，以顺利达到指定位置。

1.2 鸽群算法

在飞行过程中，鸽群具备非常突出的导航能力以及辨识方向的能力。研究者在对它们进行长时间的研究后，受到启发，创建了相应的鸽群算法(Pigeon-Inspired Optimization，PIO)。PIO算法重点根据两个方面形成，即地磁算子、地标算子。不断地对二者进行迭代处理，可以快速运算得到其中代表性粒子的速度数据，从而明确种群的最优数据。

引进相应的地磁算子。地磁算子迭代更新的方法：以和表示第只鸽子所在的位置和速度。在每轮迭代中，鸽群中的个体都可以用公式(1)(2)计算并更新个体的速度和位置。

()=(-1)e-+[-(-1)]

(1)

()=(-1)+()

(2)

式中：表示地磁算子；表示随机数；表示当前全局最优位置。

引进相应的地标算子，鸽群按照其当前的分布情况，评估目前的坐标与目的地是否相同。若方位相似或者相同，鸽群继续前进，直奔最终地点；若相反，则令群体的中心位置为目标，调整自身的行为。在不断迭代后，种群的规模会下降。以第次迭代为例，地标算子的更新方法如下：

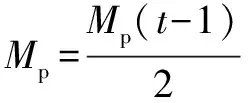
(3)

(4)

()=(-1)+[()-(-1)]

(5)

式中：为第次迭代时种群的数量；()为第次迭代后第只鸽子的位置；[()]为()位置的适应度。

结合地标算子的运算及分析，可以更高效率地确定目标位置，使鸽群更直接、稳定地到达目的地。

2 改进鸽群算法

(1)改进鸽群算法

鸽群算法的不足之处是收敛速率偏低，且局部最优出现率偏高。本文作者在原算法的前提下，在前期设置一个初始解，在进行初步处理后，能够简化算法，减少计算时间，从而能够提高计算效率。同时，在算法的地磁算子中加入相应的权重指标，提升算法在整体路径中的规划效率。权重指标的公式为

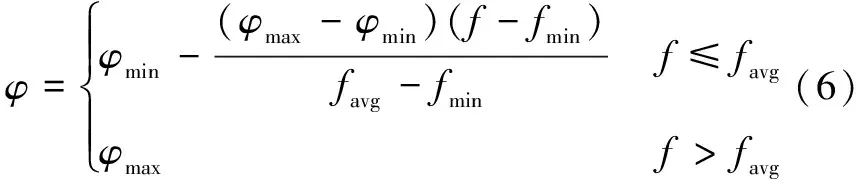
式中:、分别表示惯性权重系数的最小值和最大值；和分别表示当前鸽群内部适应度的最小值和平均值。

(2)改进鸽群算法路径规划流程

改进鸽群算法路径规划流程如图1所示。

图1 改进鸽群算法路径规划流程

3 领航跟随法编队控制

多无人车编队与单无人车进行比较，其优势主要表现为鲁棒性更好、扩展能力更强且更加灵活。以行为为基础的方法、虚拟结构法和领航跟随法是多无人车编队控制法中应用最为广泛的几种。其中，领航跟随法控制方法难度更小且效果更精准、稳定性更强，在多无人车编队控制中适用性较好。

该控制方法原理：编队内全部无人车除了领航者都是跟随者。领航者以地图信息为依据对最优路径进行确定并完成避障，将控制指令发送给领航者进而对编队整体进行控制，跟随者时刻与领航者保持相应的角度与间距，使队形得到保证。多无人车编队完成后，所有无人车都要避障，并且不能与编队内其他无人车出现碰撞现象。横纵队形和三角队形是目前最常见的编队，具体如图2所示。

图2 常见的多无人车编队队形

领航跟随法有-控制和-控制2种控制模式。-控制方式即每个跟随者无人车以一定的距离和角度跟随领航者无人车，从而实现编队队形。-控制方式即每个跟随者无人车以固定的距离跟随2个领航者无人车。现采用-控制方式，其实现步骤如下：

步骤1，领航者根据地图信息使用改进鸽群算法进行路径规划，规划出供无人车行驶的最优路径；

步骤2，领航者无人车沿着最优路径行驶，并利用避障算法进行避障，同时领航者无人车实时检测自身的位姿信息，根据使用的队形用-控制方式生成虚拟机器人的轨迹发送给跟随者无人车；

步骤3，跟随者无人车不断地接收领航者机器人发送的运动控制指令和轨迹，调整自身的速度和运动方向，沿着虚拟机器人的轨迹运动。跟随者无人车实时探测周围的环境信息，当遇到障碍物时，在原地等待一段时间，当领航者无人车通过后，跟随者无人车会行驶至领航者无人车上一时刻的位置，避开障碍物以后，跟随者恢复原本轨迹，编队队形得以恢复。

结合改进鸽群算法和领航跟随法的编队方法流程如图3所示。

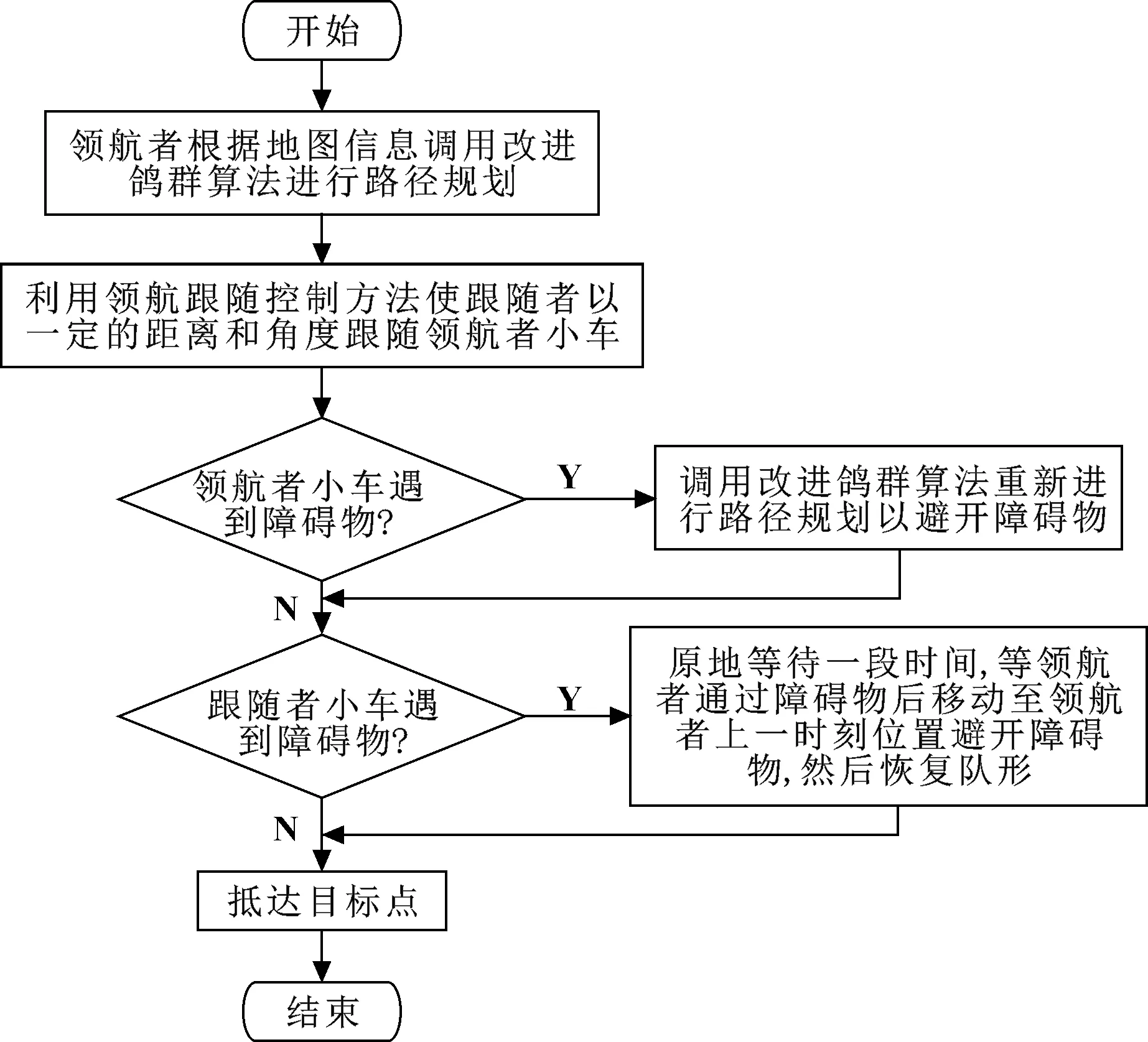
图3 编队方法流程

4 仿真实验与结果分析

4.1 路径规划仿真

为进一步验证算法的实际效果，通过MATLAB进行仿真。分析过程中，栅格尺寸确定为20×20。对相应算法进行初始化处理，借助算法获得整体最优路线。为分析算法的效果，利用PSO算法、QPSO算法进行比较分析。结果如图4所示。3种算法的收敛结果如图5所示，数据对比如表1所示。

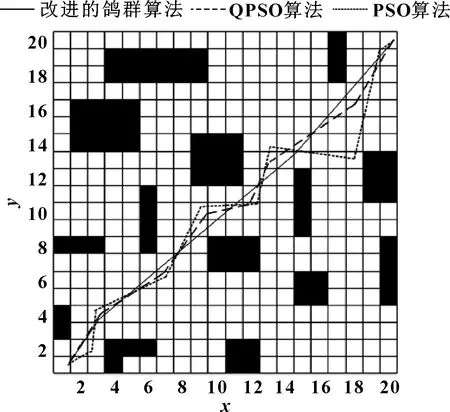
图4 3种算法的全局路径规划

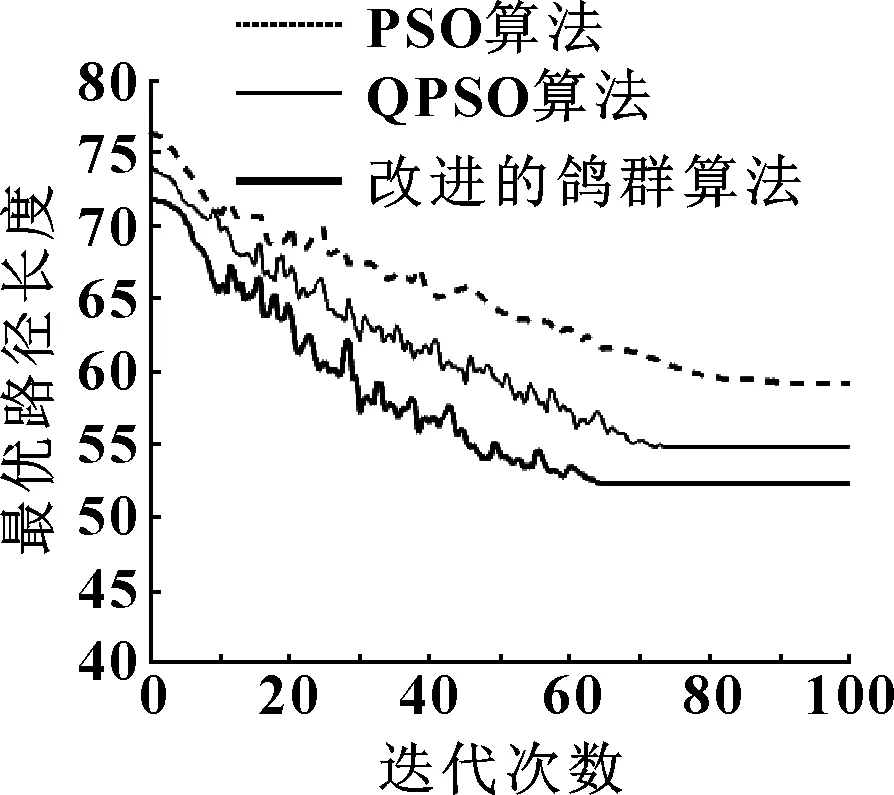
图5 3种算法的收敛比较

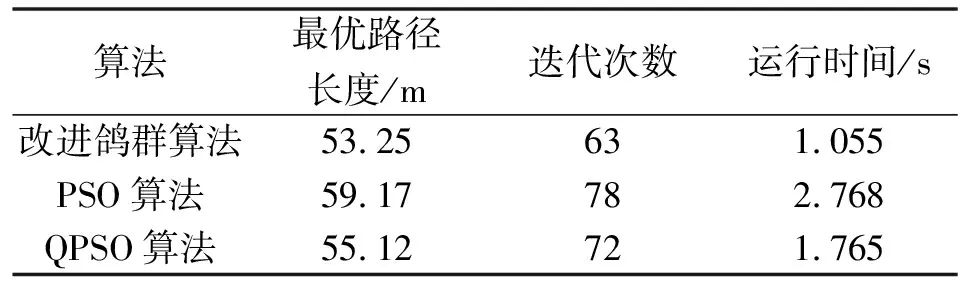
表1 3种算法的数据比较

由图4、图5、表1可以看出：PSO算法和QPSO算法虽然都可以规划出一条路径，但是从算法的运行时间、收敛性、路径长度分析，改进的鸽群算法更具有优越性。

4.2 多无人车编队仿真

以3个无人车组成三角形队形为例进行仿真验证。设定领航者、跟随者起始位置和目标点位置，领航者与跟随者在行驶途中没有遇到障碍物，无人车沿直线从起点行驶至目标点，所有无人车全程保持三角队形，行驶轨迹如图6所示。

图6 无障碍环境下无人车轨迹

在起点与终点的连线上增加一个障碍物，这时领航者无人车遇到障碍物但跟随者无人车没有遇到障碍物，当领航者无人车行驶至障碍物前时会避开障碍物行驶至一条新的路径到达终点，且跟随者无人车会与领航者无人车保持三角队形绕开障碍物并运动到目标点，如图7所示。

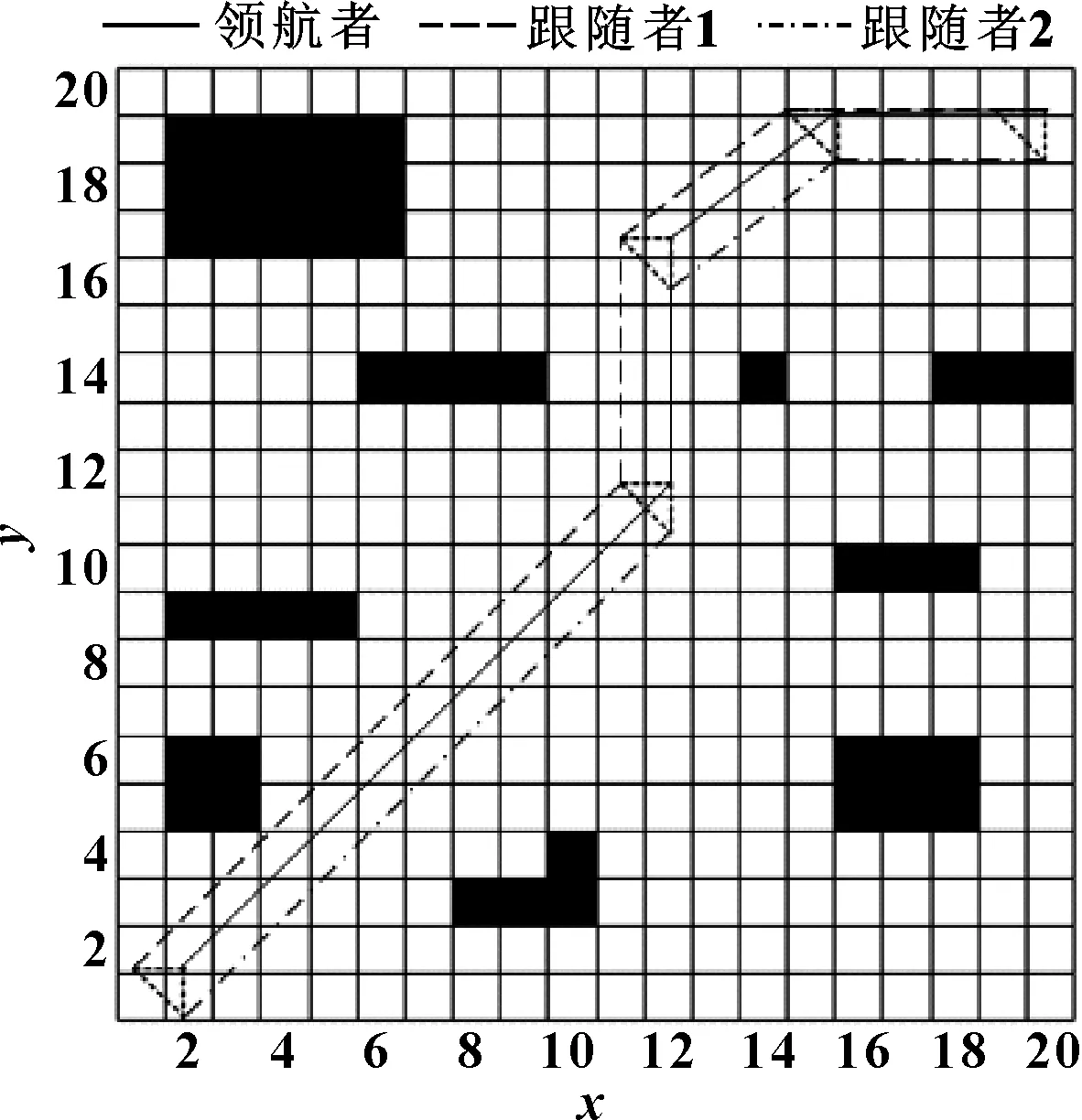
图7 领航者遇到障碍物下的无人车轨迹

当领航者无人车行驶的路线上没有障碍物但跟随者无人车行驶路线上出现障碍物，编队会进行短暂的队形变换，跟随者无人车会在障碍物前原地等待一段时间，领航者通过障碍物以后，跟随者会重复领航者行迹以实现避障，绕过障碍物后跟随者无人车会返回原虚拟无人车的轨迹上，恢复三角队形，如图8所示。

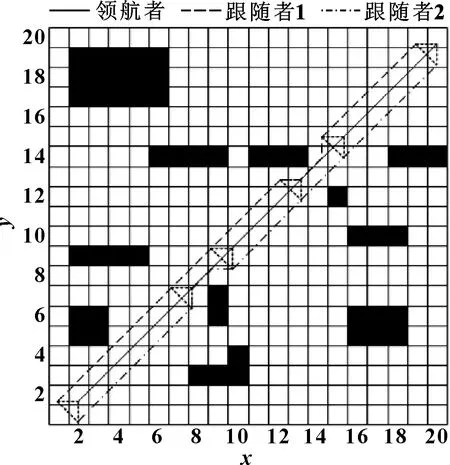
图8 跟随者遇到障碍物下的无人车轨迹

当道路只能通过一个无人车时，跟随者无人车会在障碍物前等待一段时间，当领航者无人车通过狭窄的通道后，跟随者无人车会轮流运动到领航者的位置，呈纵行队依次通过狭窄的道路，当所有的无人车通过狭窄的通道后，再恢复至设定的队形，如图9所示。

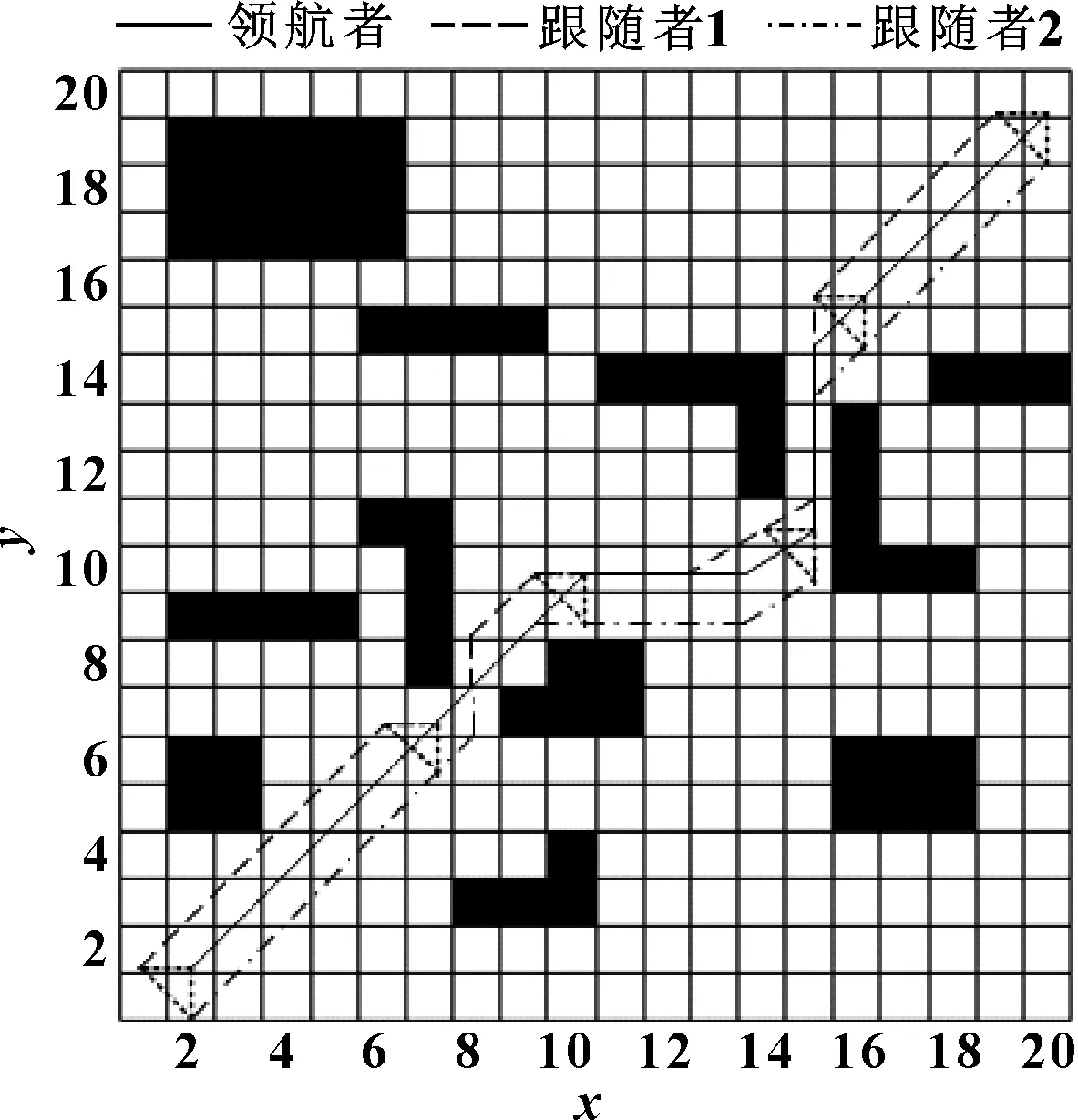
图9 狭窄环境下无人车路径轨迹

5 算法实际应用

为进一步验证该编队算法的有效性，将其运用到真实的无人车上，实现无人车的编队控制。

如图10所示，障碍物位于3台小车周围，领航者无人车使用改进鸽群算法规划出一条直线路径向前行驶，运用领航跟随法进行编队控制使后面两辆跟随者无人车以一定的距离和角度跟随领航者无人车以三角队形从起点运动到终点。

图10 无障碍环境下的编队过程

如图11(a)所示，在路径的起点和终点设置一个障碍物，领航者遇到障碍物，而跟随者未遇到，领航者小车会重新规划出一条路径绕开障碍物，此时跟随者小车依旧会与领航者小车保持队形绕开障碍物，并到达终点，过程如图11(b)—(e)所示。

图11 领航者遇到障碍物时的编队过程

如图12(a)所示，领航者无人车行驶路径上没有出现障碍物，但是跟随者无人车行驶的路径上出现障碍物，此时会进行短暂的编队队形变换，跟随者无人车在障碍物前等待一段时间，等待领航者无人车通过障碍物后，跟随者小车运动到领航者小车上一时刻的位置从而绕过障碍物，跟随者小车绕过障碍物后，恢复三角队形到达终点，过程如图12(b)—(h)所示。

图12 跟随者遇到障碍物时的编队过程

如图13(a)所示，当无人车编队通过狭窄道路环境只能通过一辆无人车时，跟随者无人车会在障碍物前等待一段时间，等待领航者无人车通过狭窄通道，跟随者小车依次运动到领航者位置，呈一字形队形或纵行队形通过狭窄通道，全部无人车都顺利从狭窄的通道通过以后，队形恢复并向终点行进，具体如图13(b)—(e)所示。

图13 存在狭窄环境下的编队过程

6 结语

本文作者将鸽群算法和领航跟随者算法相结合，通过引进相应的权重系数对鸽群算法进行改进。在仿真中，改进的鸽群算法规划的路径和运行时间比其他算法更短，验证了改进鸽群算法的优越性。领航跟随者算法在队形保持、队形变换方面都十分出色，多无人车编队在并未遇到障碍物的情况下，能够以最初编队队形一直向目标点行进，如果中途有障碍物存在或者路径过于狭窄，编队队形会适当变化以顺利通过或者避开障碍物，当所有的无人车通过狭窄环境或避开障碍物时，多无人车编队又会恢复设定的队形继续运动到终点。结果表明：所提编队方法可以控制多无人车以一定的队形有效地从起点行驶至目标点，并可以成功地避开障碍物和通过狭窄环境，该编队方法可靠、有效。研究结果为多无人车编队提供了参考。