离心力对旋转机械过盈连接的影响分析

袁玮玮，杨小强，袁龙健，刘释杰，申迎峰

(中国船舶集团有限公司第七一一研究所，上海 200072)

1 引言

文献[1]、[2]给出了光滑圆柱面在弹性范围内过盈连接计算公式，根据此公式，可对静止状态下轴与轮毂过盈连接进行设计计算。但对于旋转机械，特别是高转速轴系，如透平膨胀机、离心压缩机等叶轮转速动辄在几万转甚至十多万转，离心力使轴与轮毂各自产生变形，进而导致连接面过盈量发生变化，对连接可靠性造成了严重影响。因此，本文针对旋转轴系的过盈连接进行研究，推导了离心力作用下过盈连接的计算方法，并与静止状态下的计算结果进行对比，直观地分析离心力对过盈连接的影响。同时对旋转机械轴和轮毂的结构参数进行分析，总结出相应的趋势变化规律，从而为旋转机械过盈连接设计提供参考。

过盈连接通过轴和轮毂相互贴合产生的静摩擦力始终大于切向力来保证连接可靠，由工况参数可得到切向力，进而可知轴和轮毂所需的最小结合压强，根据以上条件，可对过盈量进行计算。下面分别对静止状态下和旋转状态下轴和轮毂的过盈量计算进行推导。

2 静止状态下的过盈连接计算

对静止状态下的过盈连接进行研究，参考材料力学厚壁圆筒相关理论[3]，假设材料处于线弹性变形阶段，不失一般性，取圆柱体截面如图1所示。

图1 静止状态下过盈连接分析模型

圆柱体截面受到的外部载荷为内压强p1和外压强p2，在截面上，以半径为ρ和ρ+dρ的2个相邻圆柱面和夹角为dφ的2个相邻径向面，从平面上取一微元abcd，变形后为a′b′c′d′，则其周向应变εφ与径向应变ερ分别为

以上应变分别对应周向应力σφ和径向应力σρ，则微元上静力平衡方程为

在线弹性的情况下，由广义胡克定律得到应力、应变之间的关系

式中E——弹性模量

v——泊松比

联立以上各式，得

则上述静力平衡方程可化为由位移u表示的平衡方程

解上述齐次微分方程，计算得到u的通解为

式中A、B——积分常数

由边界条件

ρ=r1,σρ=-p1

ρ=r2,σρ=-p2

则可得

则截面上任一点的径向位移u为

2.1 静止状态下轴过盈量计算

对轴进行计算，已知边界条件

p1=0，p2=pf

式中pf——过盈连接所需的最小结合压强

则轴截面上任一点的径向位移u的计算公式为

式中 下标s——轴(下同)

轴的结合面为外径，即当ρ=r2时，径向位移us为

此径向位移us即为轴的过盈分量。

2.2 静止状态下轮毂过盈量计算

对轮盘进行计算，已知边界条件

p1=pf，p2=0

则轮毂截面上任一点的径向位移u的计算公式为

式中w——表示轮盘(下同)。轮毂的结合面为内径，即当ρ=r1时，径向位移uw为

此径向位移uw即为轮毂的过盈分量。

则静止状态下轴和轮毂结合面过盈量δstatic为

δstatic=uw-us

3 旋转状态下的过盈连接计算

对旋转状态下的过盈连接进行研究，参考材料力学旋转圆盘相关理论[3]，分析模型与图1一致，额外增加一项由旋转导致的离心力，如图2所示。

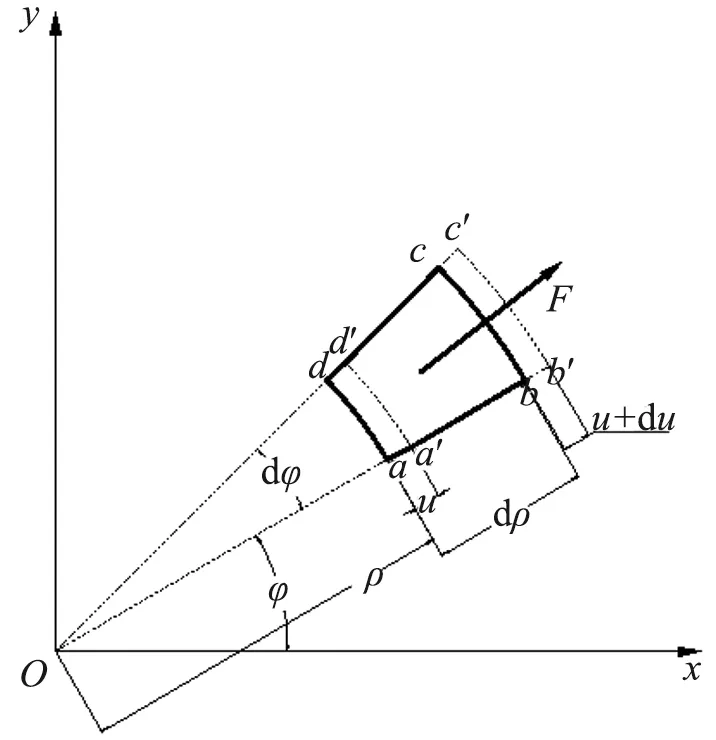
图2 旋转状态下过盈连接分析模型

若角速度为ω，材料密度为ρ0，则单位体积上的惯性力F为

F=ρ0ω2ρ

根据达朗贝尔原理，建立平衡方程

整理后，得

解上述非齐次微分方程，得到通解u

则应力为

3.1 旋转状态下轴过盈量计算

对轴进行计算，边界条件为

ρ=r1,σρ=0

ρ=r2,σρ=-pf

得到方程组

解得

则轴截面上任一点的径向位移u为

3.2 旋转状态下轮毂过盈量计算

对轮毂进行计算，边界条件为

ρ=r1,σρ=-pf

ρ=r2,σρ=0

则得到方程组

解得

则轮盘截面上任一点的径向位移u为

则旋转状态下轴和轮毂结合面过盈量δrotate为

4 参数分析

给定初步输入参数，如表1所示。分别对转速n、结合面半径rs2(rw1)、轴内半径rs2、轮毂外半径rw2等参数进行分析，模型参数示意图如图3所示。

图3 模型参数示意图

4.1 转速n

根据表1输入参数，计算不同转速下所需的最小过盈量，计算结果如图4所示，图中红色实线表示随转速变化所需的最小过盈量；为更清晰地体现转速对过盈量的影响，作出辅助线(蓝色虚线)，表示静止状态下(即不考虑转速影响)所需的最小过盈量。

图4 转速对过盈量的影响

表1 输入参数

由图可知，转速较低时，离心力对过盈量的影响较小；随着转速升高，离心力对过盈量的影响越来越明显；高转速时，离心力对过盈量的影响成为过盈连接设计计算中一个重要的组成部分。

4.2 结合面半径rs2(rw1)

保持表1中其他输入参数不变，改变结合面半径rs2(rw1)，计算结果如图5所示。

图5 结合面半径对过盈量的影响

由图可知，转速较低时，结合面半径rs2(rw1)越小，所需的最小过盈量越大；随着转速升高，曲线均出现上升，但rs2(rw1)值越大，曲线上升速度越快；达到某一临界点时，曲线出现交点，此时，所需的最小过盈量相等；转速继续升高，rs2(rw1)值越大，所需的最小过盈量越大。可以看出，结合面半径rs2(rw1)越大，曲线越陡，即转速对所需最小过盈量的影响越明显。

4.3 轴内半径rs1

保持表1其他参数不变，改变轴内半径rs1，计算结果如图6所示。

图6 轴内半径对过盈量的影响

可以看到，轴内半径rs1值增大，所有转速下所需的最小过盈量均会增加；相邻曲线的间距表明，随着rs1逐渐逼近rs2(即轴的壁厚逐渐减小)，所需最小过盈量增加速度越来越快。

4.4 轮毂外半径rw2

保持表1其他参数不变，改变轮毂外半径rw2，计算结果如图7所示。

图7 轮毂外半径对过盈量的影响

可以看出，改变轮毂外半径rw2，转速较低时，所需最小过盈量几乎不受影响；转速较高时，rw2值越大，所需最小过盈量越大，并且rw2对所需最小过盈量的影响愈加显著。

5 结论

针对旋转机械过盈连接设计，本文分别推导了静止状态下与旋转状态下过盈连接的计算方法，并对两者计算结果进行对比，结果表明：转速较低时，离心力对过盈量的影响较小；随着转速升高，离心力对过盈量的影响越来越明显；高转速时，离心力成为过盈连接设计计算中的重要因素之一。同时，对旋转机械轴和轮毂的结构参数对过盈量的影响进行分析，总结出相应的趋势变化规律，从而为旋转机械过盈连接设计提供参考。