融合活塞杆轴心位置特征的往复压缩机多源信号故障诊断模型

冯泽江，骆敏珠，邓 翔，梁永龙，徐建平

(中国石油西南油气田分公司川中油气矿，四川 遂宁 629000)

1 引言

往复压缩机运动部件多、结构复杂，在往复惯性力、气体力、摩擦力作用下活塞、活塞杆、连杆等部件故障率较高。炼油、化工、天然气等领域的机组活塞力较大，通常为数十吨，甚至上百吨，连杆轴承磨损、活塞杆断裂频发，是困扰企业往复压缩机安全、可靠运行的难题。

已有研究学者采用各类信号分析方法开展往复压缩机故障监测诊断技术研究，区别于离心压缩机、机泵等旋转设备，受机组运动特性与故障机理影响，往复压缩机采用常规的振动信号频率分析手段进行故障诊断难度大。刘江等[1]基于气阀阀盖温度运行规律建立了气阀故障智能预警模型；韩亚洲等[2]采用参数优化主成分分析(upport vector machines，SVM)处理振动信号，对压缩机气阀故障取得了良好诊断效果；唐友福等[3]建立了基于神经网络的往复压缩机气阀故障诊断，处理压缩机动态压力信号；陶红新等[4]基于活塞杆载荷分析完成了压缩机典型故障诊断；李晓博[5]等研究了往复压缩机活塞杆的自激频率特征提取方法，通过小波降噪有效提取了活塞杆的自激振动频率。然而，上述均采用单一源数据的诊断，已愈加不满足当前具有复杂结构压缩机的诊断需求。

结合压缩机故障在多种特征上的综合映射关系，已有学者开展了基于多源数据融合的诊断方法研究。舒悦等[6]通过建模仿真获得气阀泄漏理论数据，融合压力、温度等参数特征建立有效的气阀泄漏故障诊断方法；彭琦等[7]使用概率神经网络处理振动、温度、位移数据，对往复压缩机多故障诊断取得了良好效果；赵雨薇等[8]构造融合多源数据的多维特征矩阵，利用核主元分析方法对多维特征矩阵进行降维，构建状态子空间并进行典型故障预警；唐松林等[9]提出了一种基于主成分分析(Principal Component Analysis，PCA)与主成分分析(support vector machines，SVM)的典型故障诊断方法，对振动、位移数据进行处理；Farzaneh-Gord等[10]基于曲柄转角的零维数值计算方法，运用多测点振动数据，分析往复式天然气压缩机阀门故障；Pichler[11]等基于多类振动数据，分析压缩机变工况下阀门故障的特征变化特性；Wang等[12]人运用多测点声发射信号，分析阀门内部的信号随开关的变化，作为阀门故障的参考。然而，由于缺乏案例，活塞杆数据作为典型压缩机典型信号之一被长期忽视，上述文献缺乏活塞杆数据与故障的关联性的研究。

近年来，随着往复压缩机状态监测系统的应用，越来越多的机组同时安装了活塞杆竖直、水平位移传感器，两个方向位移信号可实现对活塞杆运行状态的有效监测[13]，对活塞杆、活塞组件故障，如拉缸、支承环磨损、活塞杆断裂等故障的预警诊断具有重要作用[14]。王庆锋[15]47-52等基于在线监测系统数据提取了活塞杆轴心动态能量指数，评价活塞杆实际运行状态；活塞杆轴心位置特征提取与故障诊断方面，江志农等[16]提出了基于谐波小波的活塞杆轴心轨迹特征提取方法，可诊断典型的活塞杆断裂、活塞组件磨损等故障；周超等[17]针对变负荷工况下往复压缩机活塞杆轴心轨迹特征提取方法开展研究，采用信息熵提取活塞杆轴心位置点包络特征并通过流形学习进行特征降维，实现了压缩机运行负荷的自动识别；张旭东等[18]利用改进的离散点轮廓包络方法提取活塞杆轴心轨迹特征，建立了基于BP神经网络(Back Propagation，BP)的故障诊断模型。上述对于活塞杆信号特征提取的研究已较为深入，但仍有可提升空间。

笔者基于已有研究成果，开展多源信号融合的故障诊断模型研究。针对现有轴心位置离散点轮廓特征提取方法较为复杂，对计算机性能要求较高的问题，提出了一种基于坐标转换的活塞杆轴心位置离散点轮廓特征快速提取方法，将二维空间坐标系中的离散点转化到极坐标系，通过坐标转换采用三次Hermite多项式插值法提取包络特征；进一步，建立了一种多源数据特征融合的故障诊断模型，将自编码器网络[19]数据特征与故障机理信号特征进行融合并降维，应用多种故障案例数据进行测试验证，取得了良好效果，显著提升了对往复压缩机常见故障的诊断准确率。

2 活塞杆轴心位置离散点轮廓

活塞杆轴心位置示意图如图1表示。

图1 活塞杆轴心位置示意图

其中Y——竖直坐标轴，μm

X——水平坐标轴，μm

R——活塞杆半径，μm

RX——水平传感器采集到的活塞杆位置相对变化量，μm

RY——竖直传感器采集到的活塞杆位置相对变化量，μm

O0——初始时刻，活塞杆轴心的坐标，μm

在初始时刻，活塞杆轴心的坐标为O0(0，0)；伴随机组运行，活塞杆位置改变，运动到图1中的虚线圆圈位置，轴心的坐标改变为O1(x1，y1)。因电涡流传感器采集电压信号为负，可知当活塞杆距离传感器距离变远时，RX与RY为负，反之为正。

由图1进一步可知

(R+RX+x)2+y2=R2

(1)

同理可得

x2+(R+RY-y)2=R2

(2)

令A=R+RX，B=R+RY将公式(1)、(2)联立，得

(3)

求得x，y存在两组解，根据活塞杆实体结构可排除一组无效解，从而获得活塞杆轴心位置解。

一组典型的活塞杆沉降与偏摆波形数据如图2所示。

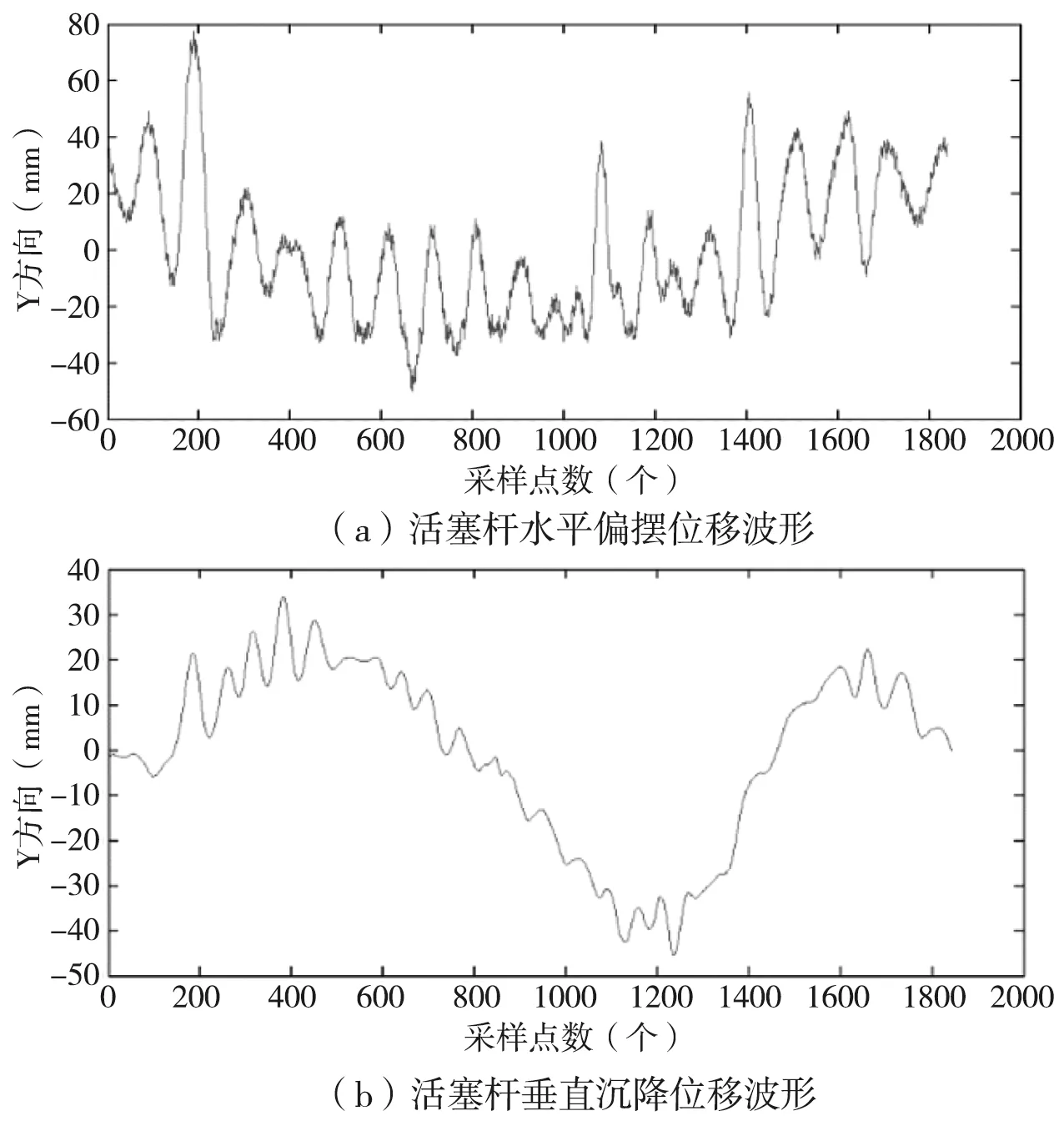
图2 活塞杆沉降与偏摆波形数据

根据活塞杆结构，由公式(3)计算获得活塞杆轴心位置点分布。

活塞杆轴心位置点分布及坐标系构建图如图3所示。

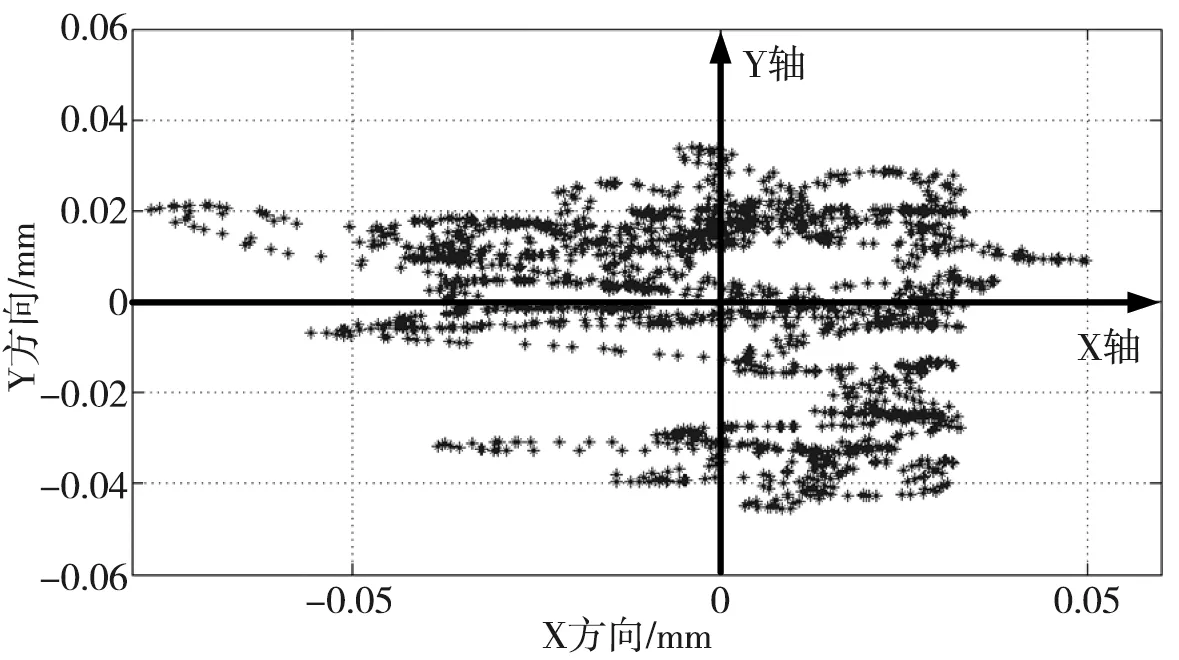
图3 活塞杆轴心位置点分布及坐标系构建图

采用公式(4)计算轴心位置离散点的分布中心O2(x2，y2)，过中心点建立极坐标系，以竖直方向为极轴，如下式所示。

(4)

(5)

式中N——轴心位置点的总数

Li——轴心到中心点的距离，mm

θi——轴心到中心点的距离Li及与极轴之间的相对夹角

进一步，定义各离散点极径为Y′轴、极角为X′轴，将轴心位置点投影二维分布转换到新的X′-Y′坐标系中。

X′-Y′坐标系内的轴心位置点分布图如图4所示。

图4 X′-Y′坐标系内的轴心位置点分布图

可见，将平面坐标系中的离散点转化为类似时域振动波形的形式是可行的。从而，笔者采用成熟的振动波形轮廓包络方法提取坐标系转化后的离散点上包络线。

提取过程采用基于基函数的分段3次Hermite多项式插值法提取X′-Y′坐标系中离散点的上包络线，具体过程如下式所示。

H3(x)=h0(x)y0+h1(x)y1+g0(x)m0+g1(x)m1

(6)

(7)

(8)

式中x、y——X′-Y′坐标系中的坐标值，μm

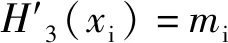
h0(x)、h1(x)、g0(x)、g1(x)——基于x、y的插值基函数

经过处理后，X′-Y′坐标系内的轴心位置点上包络线提取结果如图5所示。

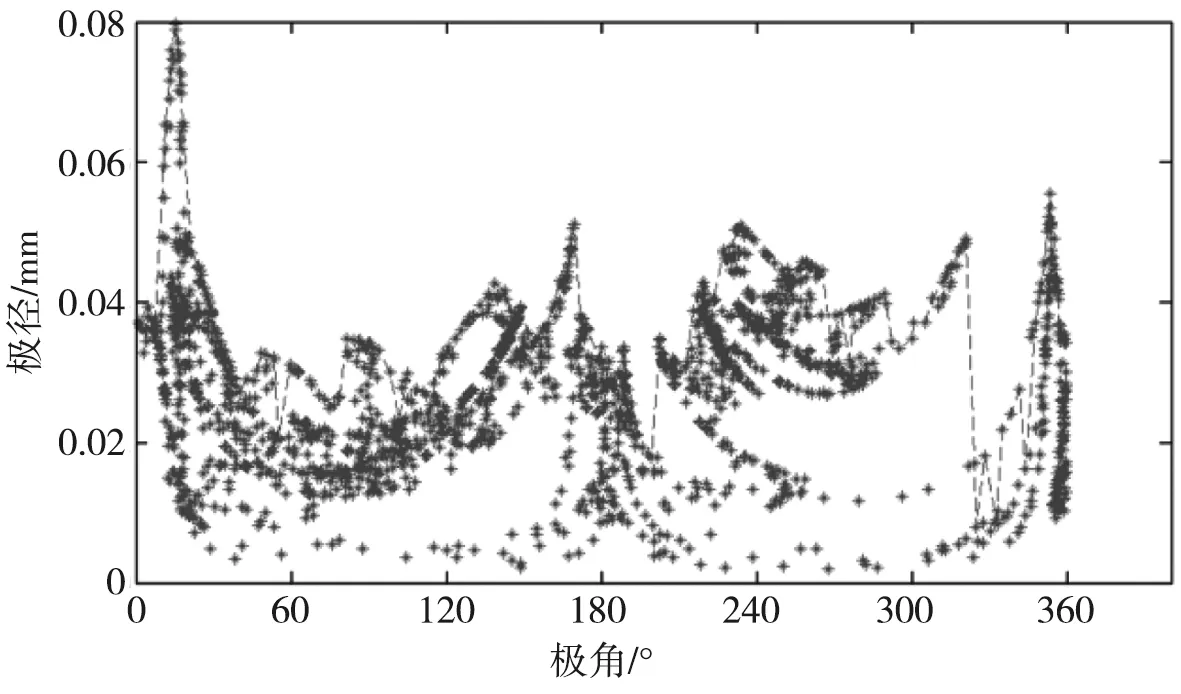
图5 X′-Y′坐标系内的轴心位置点上包络线提取结果

上述结果进行坐标逆变换后即可得到原有轴心位置点投影二维分布的外包络线，所提方法获得的轴心位置点的外包络线如图6所示。

由图6可看出，除小部分点外轮廓提取效果稍差外，大部分点提取效果良好，可表征轴心位置离散点的分布特征。

图6 所提方法获得的轴心位置点的外包络线

3 仿真与实际数据应用验证

上述过程通过一系列坐标系变换和包络线提取可得到轴心位置离散点的外围轮廓，笔者为了验证所提方法的有效性，分别采用仿真数据与真实机组活塞杆轴心位置点数据进行测试验证。

实际应用中，由于不同压缩机监测系统数据采集采样率、采样点等设置不同，不利于方法统一标准下的验证。因此采用计算机仿真数据集进行测试验证。

仿真数据采用以下设置：

(1)0～1之间的随机点数1000个，模拟常规数据采样率下整周期点数；

(2)随机选择其中600个点做X-Y坐标位置偏移，模拟实际轴心位置非对称分布。

选择文献[15]中的轴心位置离散点精确包络提取方法进行对比，结合极限点包络、常规凸包络，及笔者提出新方法的具体效果，获取包络结果。

仿真数据离散点分布与包络特征提取结果如图7所示。

图7 仿真数据离散点分布与包络特征提取结果

仿真位置点轮廓提取方法计算时间对比如表1所示。

对比不同方法的计算处理时间，由表1可知，提出的新方法在保证了较好轮廓特征提取的基础上，时间相对参考文献精确处理方法下降了64.4%。

表1 仿真位置点轮廓提取方法计算时间对比

进一步，笔者以图2所示的真实往复压缩机活塞杆轴心位置点数据进行测试应用。该机组工作转速333 r/min，数据采样率为10240 Hz。

真实机组活塞杆轴心位置点轮廓提取结果如图8所示。

活塞杆轴心位置点轮廓提取方法计算时间对比如表2所示。

对比图8、图6、表2可知：三种对比方法获得的，针对实际活塞杆轴心位置离散点数据，提出的活塞杆轴心位置离散点外围轮廓提取方法同样达到了较好的处理效果，计算时间相对参考文献精确处理方法下降了33%。因此，可进一步应用于在线监测诊断系统与故障分析诊断中。

表2 活塞杆轴心位置点轮廓提取方法计算时间对比

图8 真实机组活塞杆轴心位置点轮廓提取结果

4 基于轴心位置点包络特征的故障诊断模型

基于上述研究成果，笔者在获得活塞杆轴心位置点轮廓的基础上，提出诊断模型。

融合活塞杆轴心轮廓特征的故障诊断模型如图9所示。

图9 融合活塞杆轴心轮廓特征的故障诊断模型

特征综述如下：该模型首先提取活塞杆轴心位置点轮廓面积、极轴长度、信息熵、7个Hu不变矩[20]，定义为轴心轮廓特征，简写为a类特征。基于自编码器自适应获取压缩机振动、位移、轴心轨迹特征，定义为自适应特征，简写为b类特征。再次，融合现有在线监测诊断系统机体振动、活塞杆位移、温度数据构建监测特征库，包括峭度、有效值、峰峰值、波形指标、脉冲指标、K 因子、峰值因子、偏度、重心频率、均方频率、温度值等，定义为附加特征，简写为c类特征。

轴心轮廓特征(a类)与附加特征(c类)获取过程依靠在文献[19]133-136中与已有的特征计算数学公式。自适应特征(b类)提取过程如下：首先，对水平、垂直位移源数据(二维，一个工作周期含1845个采样点，数据形式为[1845，2]，映射至角域)，运用数据预处理结构展开为一维数据并批量归一化作为自编码器的输入。

数据预处理结构如表3所示。

表3 数据预处理

其次，建立自编码器。

自编码器结构如表4所示。

表4 自编码器结构

自编码器参数与结构均在表中给出，采用优化算法为自适应运动估计算法(Adaptive Momentum Estimation，ADAM)；学习率为0.001；训练步数为200；损失函数为均方误差(Mean squared error，MSE)；自编码器Dense层采取sigmoid激活函数，以自适应获取水平、垂直位移数据的特征。

最后，笔者采用流形学习(t-distributed stochastic neighbor embedding，TSNE)方法进行数据降维，在活塞杆断裂故障下，以类内/类间距最小，获得不同故障的敏感特征库。

敏感特征获取模型如表5所示。

表5 敏感特征获取模型

基于故障模拟实验台进行典型故障模拟及历史案例数据，共获取了活塞杆断裂、气阀泄漏、活塞组件磨损、撞缸故障各600组样本(正常300组，故障300组)，一组样本包含一组轴心轨迹数据，一组振动数据，一组位移数据。对于每一类故障运用上述振动模型进行诊断，其中随机抽取300组样本(正常150组，故障150组)用于训练，其余300组用于测试。最终得出典型的活塞杆断裂、气阀泄漏、活塞组件磨损、撞缸故障的测试组敏感特征集可视化提取结果。

活塞杆断裂故障敏感特征集可视化提取结果如图10所示；

气阀泄漏故障敏感特征集可视化提取结果如图11所示；

图10 活塞杆断裂故障敏感特征集归一化并可视化提取结果

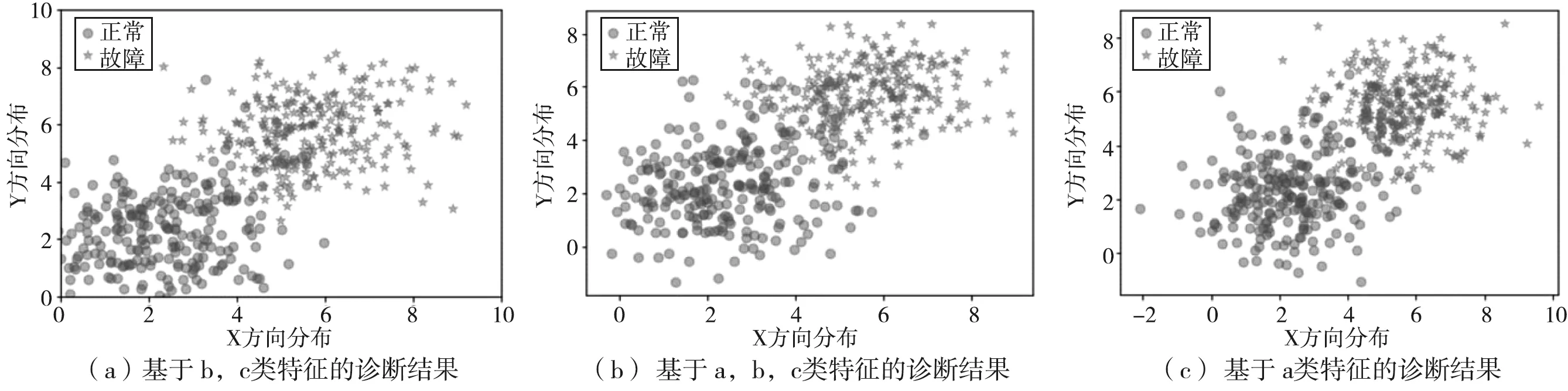
图11 气阀泄漏故障敏感特征集归一化并可视化提取结果

活塞组件磨损故障敏感特征集可视化提取结果如图12所示；

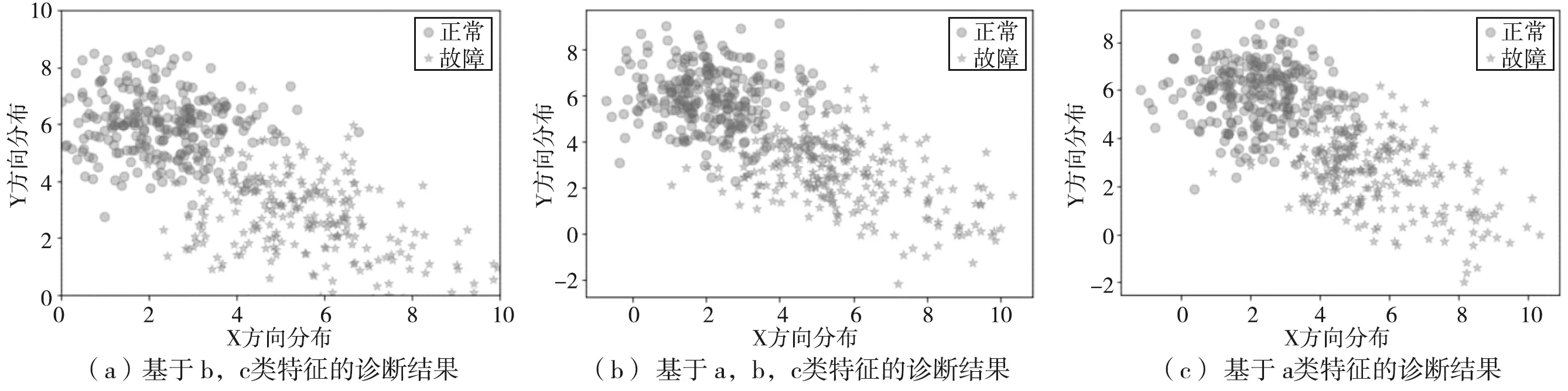
图12 活塞组件磨损故障敏感特征集归一化并可视化提取结果

撞缸故障敏感特征集可视化提取结果如图13所示。

图13 撞缸故障敏感特征集归一化并可视化提取结果

从上述图10能够看出，a类特征对活塞杆断裂故障较为敏感。

从上述图11能够看出，a类特征对气阀泄漏故障敏感性差。

从上述图12能够看出，a类特征对活塞杆磨损故障敏感性一般。

从上述图13能够看出，a类特征对撞缸故障敏感性差。

综上，当含有轴心位置离散点轮廓特征时，活塞杆断裂故障区分程度最大，活塞组件磨损故障次之，证明了活塞杆轴心位置离散点轮廓特征对活塞、活塞杆故障的高敏感性。

笔者进一步利用径向基(Radial Basis Function，RBF)神经网络建立故障分类模型，对历史故障案例数据进行测试应用，取得了较好的效果。

往复压缩机典型故障案例数据验证结果如表6所示。

表6 往复压缩机典型故障案例数据验证结果

由表6结果可知，对气阀泄漏、撞缸故障，由于故障对活塞杆位移信号影响较小，因此故障诊断模型对轴心位置轮廓特征不敏感；而对活塞杆断裂故障、活塞组件磨损故障，则影响较大，说明活塞杆轴心位置离散点轮廓特征对故障诊断诊断影响较大，是故障的敏感特征。

5 结语

往复压缩机结构复杂、故障易损件多，常用的基于单一源数据的故障诊断方法难以适应压缩机故障诊断需求。笔者针对上述问题，提出了一种融合活塞杆轴心位置特征的多源信号故障诊断模型，实现了对振动特征、温度特征、位移特征及活塞杆轴心位置特征的集成应用。

具体的研究结论如下：

(1)本研究提出了一种基于坐标转换的活塞杆轴心位置点轮廓特征提取方法，显著提升了计算效率，可应用于往复压缩机、活塞发动机的活塞杆位移在线监测及其特征提取。

(2)建立了多源信号融合的故障诊断模型，采用压缩机常见故障案例数据进行了测试验证，新的故障敏感特征集与诊断模型对活塞杆及活塞组件故障诊断效果良好。

后续将继续开展多源信号融合的往复压缩机故障诊断方法研究，一方面，在模型中进一步融入动态压力特征、多类热工参数特征等，以提升特征挖掘的全面性和故障覆盖能力；另一方面，开展特征融合方法研究，提升模型计算效率。最终，将故障智能诊断方法集成到在线监测诊断系统中，进行推广应用。