防自转机构间隙对涡旋压缩机切向泄漏影响分析

赵 嫚，李 通，安雄雄，杨 洋

(兰州理工大学 石油化工学院，甘肃 兰州 730050 )

1 引言

涡旋压缩机作为一种容积式流体机械，因其具有结构简单、体积小、效率高、可靠性高和易于操作的特性，被越来越多的应用于工业、农业、医疗、交通运输等领域[1]。压缩机运行时，为实现气体的吸气、压缩和排气，动涡盘需做公转平动，但压缩腔中气体力会引起动涡盘自转，故压缩机结构上设有防自转机构。常见的防自转机构有：十字滑环、圆柱销、滚珠轴承、球型连轴器、小曲拐和零齿差防自转机构等。防自转机构摩擦副处的加工误差、运行磨损等因素导致的动涡盘自转，使动、静涡旋齿不能精确啮合，影响压缩机性能。对此许多学者开展相关问题研究，E.Morishita等分析了涡旋压缩机的动力学特性，建立了动涡盘以及十字滑环的受力模型[2]。李超等对十字滑环防自转和带有径向随变机构的涡旋压缩机进行了研究，建立了径向随变机构运动简图，并对其进行了动力学研究分析[3]。李超等根据曲柄销防自转压缩机的结构，分析了机构尺寸误差引起的动涡盘自转误差模型，通过算例对曲轴回转一周密封间隙的变化对压缩机气密性、稳定性、安全性的影响进行了讨论[4]。刘兴旺等利用有限元软件分析了实时接触状态和摩擦力分布情况，并计算出十字滑环的摩擦损失功率[5]。朱伟等通过并对十字滑环凸键处应力进行有限元分析，分析了十字滑环的失效原因[6]。郑尚书等针对滚珠防自转机构的动力特性问题，对滚珠的疲劳强度和寿命进行了分析讨论[7]。Siyu Zheng等对CO2涡旋压缩机进行了数值研究，得到了切向泄漏流的发展特性[8]。李正等利用计算流体力学方法研究切向泄漏对涡旋压缩机工作腔流场分布影响[9]。樊灵提出了涡旋压缩机自转误差灵敏度的定义，并且提出了计算动态啮合间隙的方法[10]。其中针对十字滑环防自转机构的研究主要集中在其动力特性和摩擦磨损方面，对其摩擦副间隙与切向泄漏的关系没有提及。

本文以某十字滑环防自转机构涡旋压缩机为研究对象，建立了压缩机构件的简化模型，结合动涡盘以及十字滑环的动力特性，推导了动涡盘自转角的理论计算式。通过自转后切向泄漏间隙示意图建立了动涡盘自转角对切向泄漏通道变化量影响的关系式，并结合算例进行了分析讨论，得到十字滑环防自转机构摩擦副间隙对压缩机切向泄漏间隙及切向泄漏量的影响规律。

2 机构模型

2.1 压缩机构件

图1为十字滑环防自转机构与动涡盘、支架体的装配示意图。动涡盘在曲轴的带动下旋转，十字滑环在动涡盘的带动下沿支架体滑槽做往复直线运动。支架体限制了十字滑环的自转，也就限制了动涡盘只能在与十字滑环连接的凸键滑动方向做运动，动涡盘实现公转平动。运动特性决定了十字滑环与支架体和动涡盘的滑槽之间均存在间隙，本文只研究十字滑环凸键与动涡盘背面滑槽之间的摩擦副间隙对切向泄漏间隙的影响。

图1 十字滑环与动涡盘和支架体的装配

2.2 十字滑环及动涡盘运动分析

依据涡旋压缩机工作原理，建立图2所示表示十字滑环，动涡盘以及主轴运动关系的机构模型。

图2 压缩机构件简化机构模型

图中O1为动涡盘中心，O2为十字滑环中心，O3为主轴中心(即静涡盘中心)。直线O1O3的距离为偏心曲轴的回转半径Ror。随着主轴的转动，十字滑环上的一对凸键A和B在x方向上沿着动涡盘上相应的滑槽相对其作往复直线运动，另一对凸键C和D在y方向上沿着机架上相应的滑槽做往复直线运动。对于动涡盘来说，其运动可以看为十字滑环相对于机架的运动和动涡盘相对于十字滑环的运动的合成。

由图可知：

十字滑环相对于机架体中心的位移

SO2=-Rorsinθ

(1)

动涡盘相对于十字滑环中心的位移

SO1=Rorcosθ

(2)

受到十字滑环的作用限制，动涡盘相对于静涡盘做公转平动，其运动轨迹是以其中心O3为圆心，回转半径Ror为半径的圆，运动方程为

(3)

即动涡盘上任意一点的运动轨迹是以回转半径为中心的圆，所以动涡盘只能相对于静涡盘公转，不能自转，从而实现了公转平动。

3 摩擦副间隙与切向泄漏间隙数学模型

3.1 切向气体力及自转力矩

沿偏心轴切线方向施加在动涡盘上的气体作用力，称为切向气体力Ft。圆渐开线为涡齿的动涡盘上受到的切向气体力为

(4)

式中ps——吸气压力

P——涡旋体节距

h——涡旋体高度

N——压缩腔对数

εi——压力比

切向气体力作用于动、静涡盘基圆中心连线O1O3的中心上，如图3所示。对动涡盘产生了使其绕其中心O1顺着曲轴旋转方向自转的力矩Mr，则

图3 切向气体力作用示意图

(5)

3.2 动涡盘自转角

自转力矩作用下，动涡盘产生的自转角θro与十字滑环摩擦副间隙Xg有关，如图4所示。

图4 自转角示意图

动涡盘中心相对十字滑环中心的位移

L=Rorcosθ

(6)

由几何关系可知

(7)

即

(8)

动涡盘自转角θro为

(9)

3.3 自转角对切向泄漏间隙的关系式

理想工作状态下，动涡盘外壁面和静涡盘内壁面在啮合点处是无间隙存在的。动涡盘自转方向与偏心轴转动方向一致，当偏心轴顺时针转动时，动涡盘发生顺时针自转，切向泄漏间隙示意图如图5所示，取理想状态下，动盘外壁面型线区域一点M，其法向角为φ。当动盘发生自转后，假设过M点的理想型线的法线交自转后实际动盘型线于M′点，其法向角为φ′。其中O1为动涡盘基圆中心。O3为静涡盘基圆中心。

图5 自转后切向泄漏间隙示意图

(10)

即：

lMM′=lO1M′-lO1M

(11)

在理想工作状态下动涡盘外型线方程为

(12)

Rt(φ)——动盘外型线切向分量

φ——啮合点法向方向角

发生自转时，动涡盘产生的自转角θro，在实际工作状态下动盘外型线方程为

lO1M′=lO1M(φ′+θro)exp[j(-θro)]

(13)

基于涡旋压缩机性能要求，动涡盘自转角应尽可能小。将(13)代入(11)式，当θro很小时，φ≈φ′，整理得

lMM′=Rn(φ′+θro)-Rn(φ)

(14)

对于型线为基圆渐开线时

Rn(φ)=c10+c11(φ+c12)

(15)

将(14)和(15)联立可得

lMM′=c11(φ′+θro-φ)≈aθro

(16)

由分析过程可知，动、静涡盘切向泄漏间隙变化量与动涡盘自转角、涡旋压缩机型线方程和啮合点法向角有关。对于圆渐开线，联立(9)和(16)式可得切向泄漏间隙变化量为

(17)

式中a——基圆半径

4 算例

4.1 切向泄漏间隙变化量计算

以圆渐开线型线涡旋压缩机为例，取十字滑环与动涡盘滑槽摩擦副间隙值分别为：Xg=0.02 mm、0.04 mm、0.06 mm、0.08 mm，对切向泄漏间隙变化量δ进行了计算，结果如图6所示。

图6可看出，一定防自转机构间隙下，切向泄漏间隙在曲轴转角0°～360°范围内是变化的；变化突变发生在90°和270°，这是因为动、静涡盘的工作腔是成对出现的，动静涡旋齿一侧出现间隙，另一侧必定出现齿面的硬接触。动涡盘相对支架体运动方向改变导致转化点在90°和270°处。

4.2 自转后切向泄漏量计算

由图6可得曲轴转角为90°和270°时，切向泄漏间隙变化量最大。以两相邻压缩腔间的切向泄漏为研究对象，相关参数如下：曲轴转角θ=90°时，第二压缩腔压力p2=0.26 MPa，第三压缩腔压力p3=0.12 MPa，涡旋尺高h=40 mm，压缩介质为空气。自转后的切向泄漏模型如图7所示。

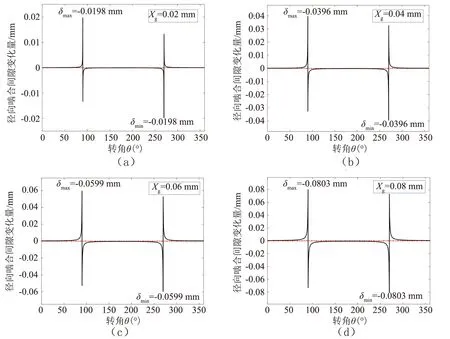
图6 动、静涡盘切向泄漏间隙变化量

图7 自转后切向泄漏模型

切向泄漏质量流量[16]

(18)

式中ψ——流量系数

A——切向泄漏面积

ph——高压腔压力

pl——低压腔压力

ρh——高压腔密度

κ——绝热指数

其中，自转后切向泄漏面积

A=δ·h

(19)

式中δ——自转后切向泄漏间隙

h——涡旋齿高度

代入压缩机相关参数，可得十字滑环与动涡盘滑槽摩擦副间隙对切向泄漏量的影响如图8所示。

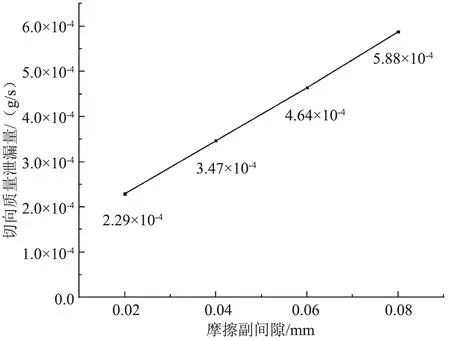
图8 切向泄漏量-摩擦副间隙

5 结语

(1)一定防自转机构间隙下，切向泄漏间隙在曲轴转角0°～360°范围内是变化的，且为周期性变化；摩擦副间隙越大切向泄漏间隙极值及泄漏量越大，切向泄漏量与摩擦副间隙近似成正比。

(2)切向泄漏间隙极值发生在曲轴转角90°和270°，且切向泄漏间隙变化量反向变化。啮合区一侧由切向泄漏间隙转变为动、静涡齿壁间的摩擦接触，另一侧则由动、静涡齿壁间的摩擦接触转变为切向泄漏间隙。