混合时滞复值神经网络的事件触发状态估计*

刘飞扬， 李 兵

（重庆交通大学 数学与统计学院，重庆 400074）

引 言

复值神经网络(CVNNs)是实值神经网络的一种扩展形式.其基于复值变量和复数算法进行设计，可以用来处理更复杂的信息，近年来已在风预测、复杂现象分类、彩色人脸识别等领域得到了深入应用[1-3].考虑到网络中放大器开关速度的限制，神经元的信息接收和传输不可避免地存在延迟，因而考虑时滞神经网络更符合实际情况.近年来，时滞复值神经网络的稳定性、同步性以及滤波问题等相关研究结果也不断涌现[4-8].

在实际应用中，由于外部环境的复杂性和测量设备的限制，往往无法完全获知神经网络的状态信息.因此，人们往往需要利用可测量的输出信息来估计神经元的状态，然后再利用估计状态来进行反馈控制[2,9-11].到目前为止，时滞实数神经网络的状态估计问题已得到了较为深入的研究，相关成果也比较丰富[12-15].例如，文献[15]针对一类实值时滞神经网络的状态估计问题进行了研究，给出了有效的估计器设计方法.近几年来，复值神经网络的状态估计问题也逐渐引起了学者们的关注.比如，文献[16]研究了延迟复值神经网络的鲁棒状态估计问题，分析了时滞和参数变化对估计器的影响.文献[17]利用采样数据设计了随机复值神经网络的鲁棒状态估计器.

另一方面，在网络传输环境下，传感器能量和网络带宽资源总是有限的.在确保系统性能的前提下，有效节省网络资源非常重要.传统的时间触发机制总是按固定周期传输信息，从而在系统性能较好时造成不必要的网络资源消耗[18-20].事件触发机制(ET)通过预先设计特定触发条件，仅在必要的时间点才执行传输任务.研究表明，事件触发机制既能有效节约网络资源又能确保系统性能.近年来，事件触发机制已被广泛用于镇定控制、状态估计、同步分析以及分布式优化[21-23].然而就笔者所知，对于事件触发机制下复值神经网络的状态估计问题，尚未得到足够的重视，相关的研究成果还非常少.

鉴于上述情况，本文研究了一类具有混合时滞的复值神经网络基于事件触发机制的状态估计问题.通过引入等待时间，并结合测量输出误差，设计了一类新的事件触发机制，有效降低了估计器更新频率，同时避免了Zeno现象发生.构造合适的Lyapunov-Krasovskii泛函，利用模型分解技巧，得到了确保误差系统全局渐近稳定的一些充分条件，并给出了基于线性矩阵不等式(LMI)形式的控制器求解方法，最后通过数值算例验证了所获得理论成果的有效性.本文的主要贡献在于：① 首次针对混合时滞复值神经网络，考虑了基于事件触发机制的状态估计问题；② 将等待时间和相对误差结合，设计了新型触发机制，既有效避免了Zeno现象，又确保了误差系统的全局渐近稳定.

1 模型描述和预备知识

为了方便表达，本文使用以下记号：

Rn表示n维 欧氏空间， Rn×n和Cn×n分别表示 n×n的 实矩阵和 n×n的 复数矩阵的集合.C ([c,d], Cn)表示 [c,d]到 Cn上的全体连续函数.对于 A∈Rn×n, AT和A-1分别表示矩阵A的转置和逆， sym(A)表示A+ AT.A＞0(或A＜ 0)表示A是正定矩阵(或负定矩阵)，表示对角复数矩阵diag(l1,l2,···,ln)的实部(虚部)，∗表示对称矩阵中的对称元素， col(·)表示一个列向量.

本文考虑具有n个神经元的混合时滞复值神经网络：

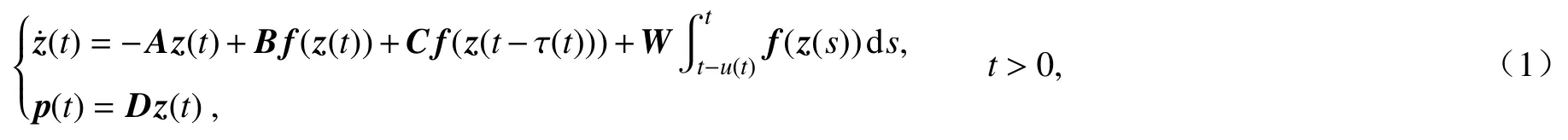
其中z(t) = col(z1(t),z2(t),···,zn(t))∈Cn表示神经元状态向量， p(t) = col(p1(t),p2(t),···,pn(t))∈Cn表示网络测量输出向量；A =diag(a1,a2,···,an)∈Rn×n＞0表示神经元放大器参数，B = (bij)n×n∈Cn×n，C = (cij)n×n∈Cn×n，W = (wij)n×n∈ Cn×n，D∈Cn×n分别表示神经元连接权矩阵、时变时滞连接权矩阵、有界分布时滞连接权矩阵和表示网络的输出矩阵； f(z) = col(f1(z1), f2(z2),···, fn(zn))表示神经元的向量值激活函数； τ(t)表示有界时变时滞，满足0≤ τ(t)≤τM，且˙(t)≤a＜1； u (t)表示有界分布时滞，且满足 0＜u(t)≤uM.本文假设模型(1)的初始条件为z(t) = φ(t),t∈[-t0,0]，其中 t0= max{τM,uM}.

为了方便表述，我们记复值信号 z(t) = x(t)+iy(t)，其中 x(t)， y(t)分别表示 z(t)的实部和虚部，i为虚数单位，并且i=

对于网络激活函数，我们给出如下一般性假设.

假设1f(z(t))可以分成实部和虚部：

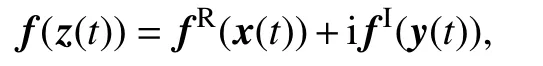
其中

假设2 对于任意的 i∈{1,2,···,n}， x1,x2∈R且 x1≠x2.存在正定实数矩阵= diag满足

当x1= x2= 0时，激活函数满足

注1 模型(1)同时考虑了有界离散时滞和分布时滞，是对已有文献所研究模型的推广[24-25].例如，当有界分布时滞未被考虑时，模型(1)退化为文献[24]中所研究的神经网络模型.当网络时滞仅含有界分布时滞，则可以得到文献[25]所考虑的模型.

为了提高网络输出和状态估计器之间的传输效率，我们基于连续观测的输出信号设计了一个具有等待时间的事件触发传输机制.具体而言，令 {tk}表示触发时间序列，且满足 0 = t0＜t1＜t2＜···， limk→∞tk=∞.触发时刻序列按如下方式确定：

其中ϵ≥0， hk＞0是给定的常数， Ω1,Ω2表示触发阈值函数的权重实数矩阵； pR(t)， pI(t)分别表示输出信号 p(t)的实部和虚部.需要指出的是，对于任意的自然数k ，两个连续触发时刻之间的时间间隔一定满足 tk+1-tk≥hk，即令d(t) = t-tk，有 hk≤d(t)，其中t表示当前时刻.因此本文设计的事件触发机制可以避免Zeno现象的发生.在事件触发机制的影响下，状态估计器所接收到的最终输入信号可以表示为

考虑事件触发机制(2)的影响，我们构造如下形式的状态估计器：

其中

注2 由于传统的周期采样可能导致资源浪费，非周期采样引起了人们的关注.事件触发是非周期采用的 一种主要方式[11,26].上述文献研究了连续时间系统的事件触发控制问题.值得注意的是，这两篇文献所采用的触发条件，都仅与相对误差演化有关，因而触发频率较快.本文设计了一种新的事件触发机制，通过引入等待时间来延长两次相邻触发之间的时间间隔.具体来说，事件触发机制(2)将两个连续触发事件之间的时间间隔 [tk, tk+1)分为两部分，即 [tk, tk+hk)和 [tk+hk, tk+1).测量值 pR(tk)， pI(tk)更新之后，需要等待秒.从开始，传感器开始持续监测触发条件(2)，直至下一触发时刻到来.与传统触发机制相比，本文设计的触发策略具有固定的等待时间，能有效避免高频触发现象.如果考虑到传感器故障，本文的触发条件更灵活，更适用于现实系统.

结合假设1，估计误差系统(3)可以等价表示为如下形式：

引理1若常数矩阵 R∈Rn×n， ζ(s) : [a,b]→Rn是一个向量函数， a＜b ，其相关的积分满足下列不等式：

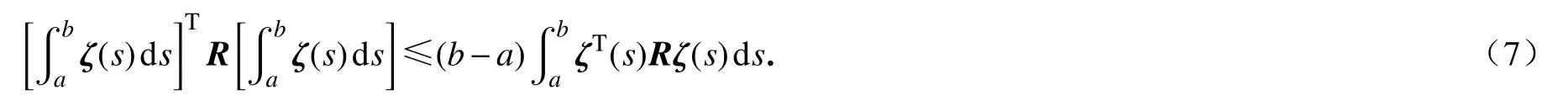
2 主 要 结 果

本节将结合系统的当前状态信息和时滞信息，建立误差系统状态全局渐近稳定的充分性判据，并给出估计器增益矩阵的求解方法.

定理1 在h， ϵ，σ为正数的条件下，若存在实数对称正定矩阵 P, Q, U, V, R1, Q1, R2, Q2，正定对角矩阵Λi(i= 1,2,···,4)，以及实数矩阵 Ω1， Ω2，Y2，Y3，T1，T2， M1， M2， P2， SR，SI和正实数 hk∈(0,h]，使得

则误差系统(6)是全局渐近稳定的，且估计器增益矩K可以设计为

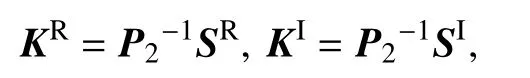
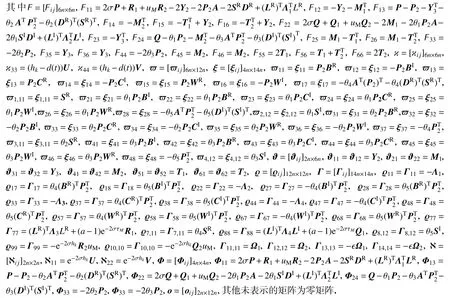
证明构造Lyapunov-Krasovskii泛函如下：

其中

由引理1，不等式(18)中积分项可变化为

由不等式(19)类似可得

其中

由假设2，存在对角矩阵Λi＞0(i = 1,2,3,4)，我们可以得到

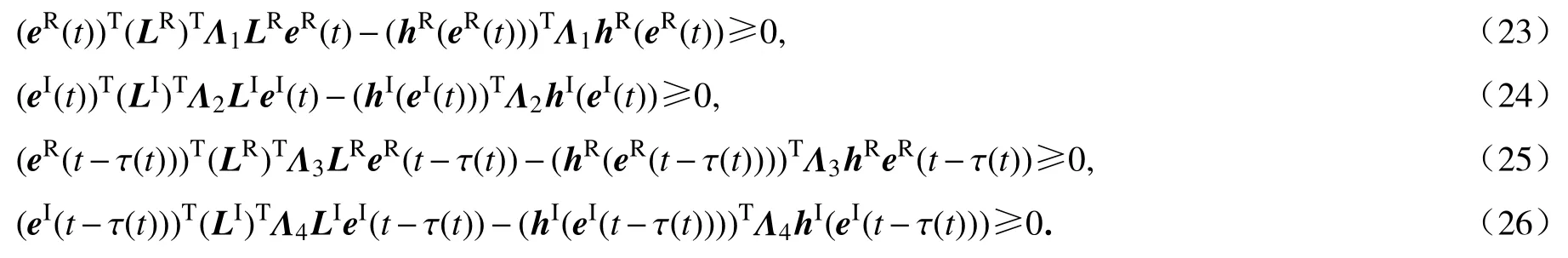
当t∈[tk, tk+hk)时，对任意的矩阵我们可以得到

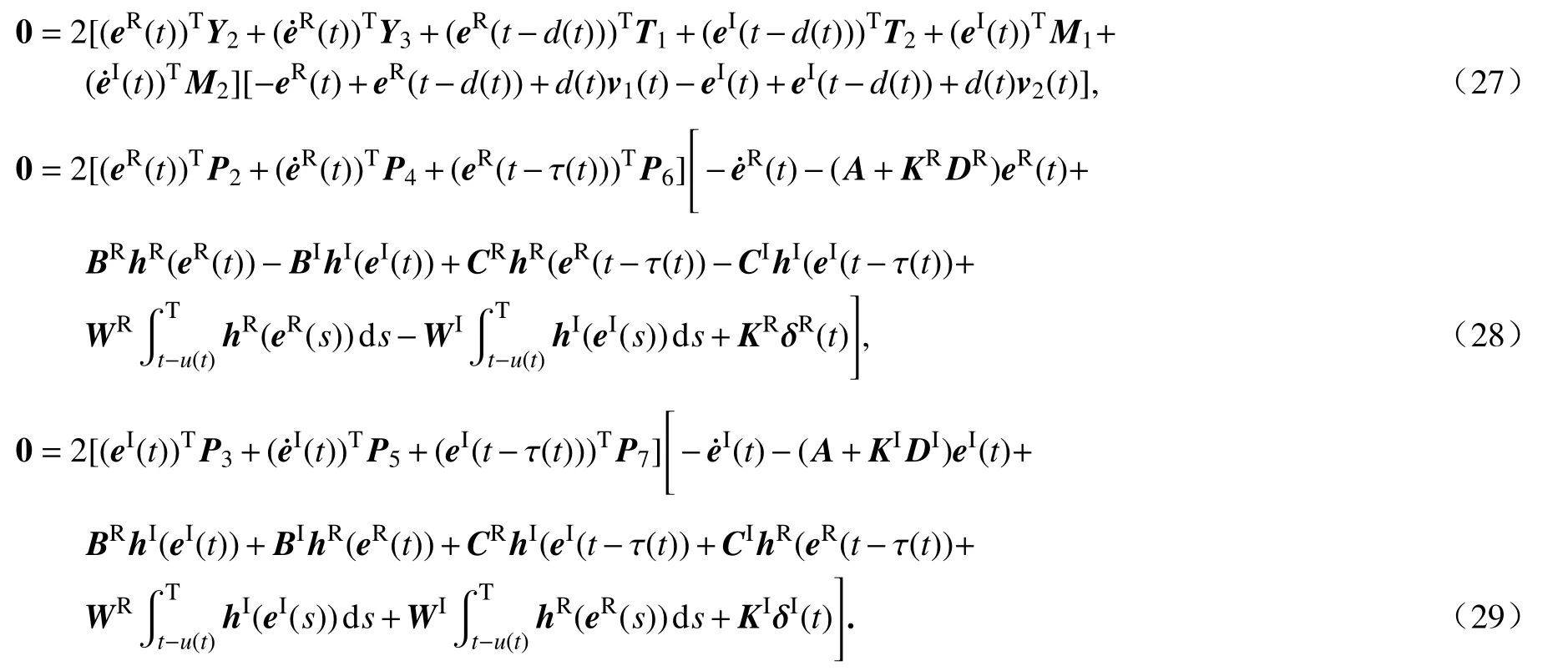
令Pk+2=θkP2(k = 1,2,···,5)，则存在实数矩阵 SR和 SI，使得成立.由式(16)、(17)及式(21)~(29)，我们可以得到

其中

令

根据不等式(8)和(9)，可以得到如下关系：

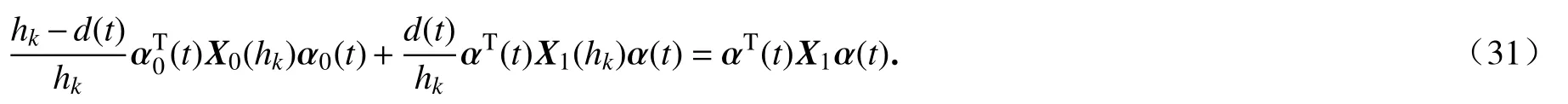
由此可知，当 X0(hk)＜0和 X1(hk)＜0时，有 V˙(t)+2σV(t)≤αT(t)X1α(t)＜0.

当t∈[tk+hk, tk+1)时，对t 进行阈值函数(2)的判断：

结合式(16)、(17)、(21)及式(23)~(29)和(32)，有

其中

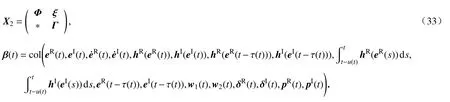
由条件(10)可得

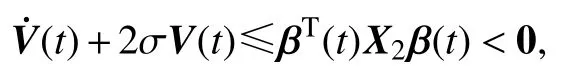
下面我们来讨论 V(t)在点tk和点 tk+hk上是否连续.显然，对于 Vi(t)(i = 1,2,3)在tk和tk+hk上均连续.对于V4(t)，由于

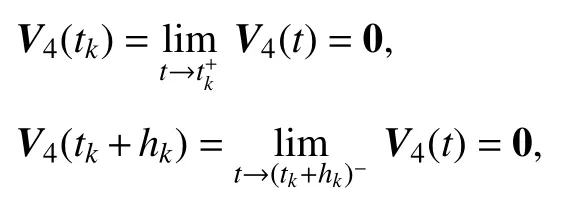
从而可以得到

因此， V(t)在tk和 tk+hk上连续，从而有 V(t)在区间 [tk, tk+hk)和 [tk+hk, tk+1)上连续.

对于 t∈[tk, tk+hk)，由上述推证过程可知 V(t)＞0且 V(t)在区间 [tk, tk+hk)上单调递减.现在对V˙(t)+ 2σV(t)≤0进行 tk→t 的积分和放缩有

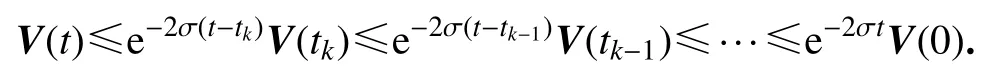
当t∈[tk+hk, tk+1)时，我们也可以得到 V(t)≤e-2σtV(0).

综上所得

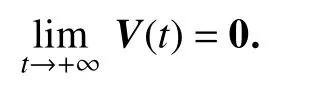
因此，误差系统是全局渐近稳定，其中 KR= P2-1SR， KI= P2-1SI.定理得证.

注3 与文献[9,12-15]中的实值状态估计结果相比，定理1针对连续时间复值信号给出了基于事件触发机制的状态估计器，并建立了误差系统渐近稳定性判据.与文献[16-17]相比，本文引入等待时间和相对误差建立的事件触发机制能有效降低更新频率，节约通讯资源，同时确保估计性能.

3 例子与仿真

本节提供了一个数值例子来说明我们的方法的有效性.考虑具有两个神经元的混合时滞神经网络，网络参数如下：

选取激活函数为 f(z(t)) = tanh(x(t))+i·tanh(y(t)).显然，假设2成立且可选取

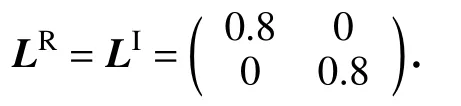
令 τM= 0.04， uM= 0.01， a =σ= 0.1， θ1=θ4=θ5= 0.04， θ2=θ3= 0.05，根据定理1，我们设计事件触发参数 ϵ= 0.1， hk= 0.05.利用MATLAB工具箱求解不等式(8)~(10)，我们可得到事件触发的矩阵和估计器增益矩阵为

从而实现了估计误差系统的全局渐近稳定.

图1~4给出了例子的数值模拟结果.为了便于计算机仿真，我们选择了步长为 0.01.令 ϵ= 0.1， hk= 0.05，a =σ= 0.1，给定时滞 τM= 0.04， uM= 0.01，初始状态向量 z(t) = [3-3i,-0.9+5i]T和观测器系统初始状态zˆ = [0,0]T.神经网络状态如图1所示；图2描述了估计系统状态轨迹；图3刻画了 ϵ= 0.1， hk= 0.05的情况下的事件触发时刻；图4描述了估计误差状态收敛的速度趋近于零.

图 1 神经网络状态Fig. 1 The state of the neural network

图 2 估计器状态Fig. 2 The state of the estimator

图 3 事件触发时刻Fig. 3 The event trigger time

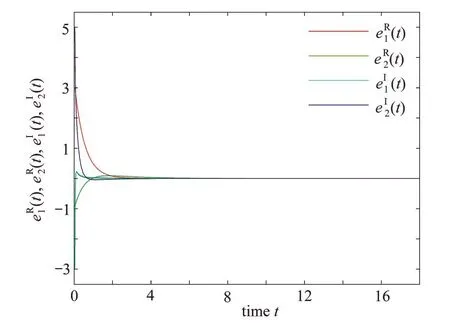
图 4 误差系统状态Fig. 4 The state of the error system

4 总 结

本文研究了一类具有混合时滞的复值神经网络状态估计问题.我们采用事件触发策略来确定何时更新估计器的误差信息，利用Lyapunov函数和比较原理进行了误差系统的全局渐近稳定性分析.最后，通过一个数值例子验证了理论结果的有效性.在未来的工作中，我们将继续研究复值神经网络在自触发情况下的 H∞状态估计以及网络诱导复杂性(如量化、错序、协议等)对复值神经网络状态估计的影响.

致谢本文作者衷心感谢重庆交通大学院级研究生科研创新基金(2021ST001)对本文的资助.