考虑记忆效应及尺寸效应窄长薄板的磁-热弹性耦合动态响应*

马永斌， 李东升

（兰州理工大学 理学院，兰州 730050）

引 言

在现代工程技术中，尽管分数阶微积分已被广泛地应用于广义热弹性领域，但目前分数阶参数并无明确的物理意义[1-3].通过改进分数阶理论，Wang和Li[4]提出了记忆依赖微分（MDD）.与传统的分数阶热弹性耦合理论相比，引入记忆依赖微分修正热弹性耦合理论有众多的优势[5-6].

虽然引入记忆依赖微分能很真实地描述材料“瞬时变化率受过去情形影响”这一现象，但经典热弹性耦合理论是基于Fourier定律建立的，这类理论描述温度的传播速度是无限大的[7].表明受到热作用的瞬间，在该材料上距离作用点无限远处可观测到热作用，这与实验结果相悖[8-9]，因此热作用后极短时间内Fourier热传导定律不再适用[10-11].为解决这一难题，学者们通过修正Fourier热传导方程提出了非Fourier热传导理论模型[12-13]，如C-V热波模型、双曲型两步模型、单相滞后模型、双相滞后模型（DPL）等.

上述对广义热弹性理论的修正均为对热方程的改进，而弹性方程仍采用经典模式，虽然可以很好地描述较大尺寸的结构，但对于微尺度结构不能满足计算精度.基于微尺度结构的理论有应变梯度理论、偶应力理论及非局部理论等[14-16].其中，Eringen提出的非局部理论更为成熟，应用也更加广泛.Eringen非局部理论认为材料中一点处应力不仅和该点处应变有关，还与材料其他点处应变有关[17].目前看来，非局部领域的研究多为基于非局部理论研究材料受热作用的力学行为[18-21].同时考虑记忆依赖效应和非局部效应的双相滞后热弹性理论尚未建立，基于该理论对多场耦合问题的研究尚未发现.

本文引入了记忆依赖效应和非局部效应修正了双相滞后广义热弹性理论，基于改进后的理论研究了受磁-热-弹耦合作用下薄板的动态响应.为微尺度薄板的设计提供了理论指导，并为分析其他材质微尺度弹性体的多场耦合提供了方法.

1 理 论 公 式

函数f 的一阶记忆依赖微分算子可表示为[4]

式中ω为时间延迟因子（ω ＞0）， K(t-ξ)为核函数，根据工程应用的需要，二者可自由选择来表征不同情况下记忆效应对材料力学行为的影响； f (t)为函数f 的时间项，ξ为积分变量；Dω为记忆依赖微分算子符号，当核函数取1时 Dω满足如下数学关系[20]：

式中x和 t 均为函数 f (x,t)的自变量.

El-Karamany和Ezzat等[21]给出了记忆依赖热传导方程形式如下：

式中k 为导热系数，q 为热流，θ为温度，∇为Hamilton算子.当记忆依赖算子中核函数 K(t-ξ) = 1，且时间延迟因子 ω→0时，该理论将退化为Biot经典热弹性理论(DCT)[22].

Tzou[23]提出了双相滞后模型，该理论下导热定律为

式中x为 坐标变量，τq为温度梯度迟滞因子，τθ为热流矢量迟滞因子.

Biot[22]的能量方程形式如下：

式中ρ为密度， CE为比热，T0为参考温度，θ为温度，e 为应变，Q 为单位质量的热源， γ= (3λ+2µ)αT，αT为热膨胀系数.

对方程（6）的两边同时求散度，并将方程（5）代入其中，化简后得

方程（7）即为考虑记忆依赖效应的双相滞后热方程.

根据Eringen提出的非局部理论，材料中一点r 处应力-应变关系可表示为[17]

按照Eringen非局部理论的微分形式，一维情况下本构方程为[17]

式中 σij(r)为非局部应力分量，为经典应力分量，为经典应变分量，为经典体积应变， e0a 为非局部参数，λ，µ为Lamé常数，δij为Kronecker符号.

2 基 本 方 程

不考虑体力和内热源，处于磁场中导体的运动方程为

式中ρ为密度，ui为位移分量，t 为时间， σij为应力分量，Fi为Lorentz力分量.

Lorentz力分量 Fi为

式中 µ0为磁导率，J 为电流密度矢量，H 为施加的磁场强度矢量.

本构方程为

几何方程为

则给出Maxwell方程组形式为

式中ε0为电导率，为磁导率，为Hamilton算子，为感应磁场，E为感应电场.

联立方程（9）和方程（12），即将非局部因子引入到本构方程中，得出考虑非局部效应的本构方程表达式：

3 模型的控制方程

如图1所示，考虑一个长为 L0的直尺状窄长薄板，材质为均匀各向同性的热弹性固体.整个材料置于初始磁场 H0中，在 x = 0的边界面处受到热作用，热作用大小随时间而变化.

图 1 板受磁场和热作用示意图Fig. 1 A plate in a magnetic field under thermal shock

本算例可以看作一维问题，所有变量都依赖于空间变量x和 时间变量t ，位移分量的形式如下：

从Maxwell方程组（14）~ （17）可得感应电场E和感应磁场h为

由方程（20）、（21）和（14），可得出电流密度：

由方程（21）、（22）和（11），得Lorentz力 Fi为

在一维情况下，方程（10）、（13）、（18）的形式如下：

把方程（1）代入方程（7）并将所得方程化为一维形式，可得一维情况下考虑记忆依赖效应的双相滞后热方程：

引入下列无量纲量对基本方程进行简化：

对方程（24）~ （27）进行无量纲化处理得（为了便于书写，略去各量右上角星号）

其中ε为热弹性耦合常数，

联立方程（24）~ （26），并进行无量纲处理可得

对于热边界条件，在 x = 0处边界面受到一个随时间变化的热载荷 f (t).对于机械边界条件，在 x = 0处边界面为自由约束.则边界条件为

初始条件为

为了与其他学者的研究[5]对照，本文周期性变化热源与国外学者所采用的保持形式一致[24]，给出热源如下：

此处常数a为 温度波的周期，t 为时间.

核函数形式取Wang和Li[4]给出的形式：

4 Laplace域下问题求解

采用以下Laplace变换公式：

由式（37）可得如下数学关系式：

采用式（37）、（38）对方程（28）~ （31）进行Laplace变换，可得

其中

磁-热-弹耦合方程为

边界条件（33）可化为

其中

这里 x＞0，求解方程（45）和（46），得出通解为

其中

由式（48）结合边界条件（44）得

将式（47）、（48）代入方程（42）得

将式（47）、（48）代入方程（41）得

5 Laplace反变换

为了得到材料在时空域中温度、位移和应力的分布，需要对拉氏域中的解进行Laplace反变换.由于在拉氏域中得到的表达式形式复杂，通过反变换公式计算时空域中的解析解是较困难的.因此，实际处理时大多都是通过编写MATLAB程序来进行数值求解.给出Laplace反变换基本公式形式如下[24]：

其中i为虚数单位，s 为Laplace变换因子， c≈α-(Ω/2π)ln Er，α是函数 f (t)的指数阶，Ω为拉氏域中的周期，Er为相对误差.

基于快速Fourier变换（FFL）将反变换基本公式近似离散，然后采用“ε-algorithm”在保证精度和收敛速度情况下对其求和从而得出反变换结果[25].给出“ε-algorithm”定义如下：

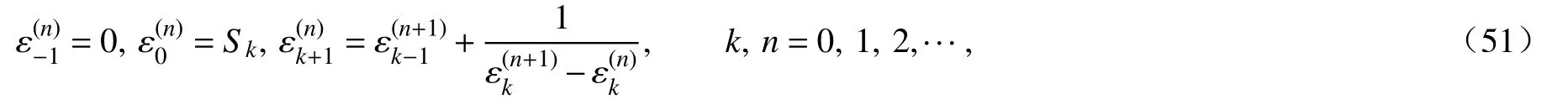
这里Sk为所需计算无穷级数的前k 项和，表示εk向量中第n个元素.

Brancik基于以上思想编写了Laplace反变换程序[25]，本文通过参照该程序思路编写反变换程序解决了所分析的问题.

6 数 值 分 析

在前文中我们建立了模型的基本控制方程，由控制方程结合相应的初始条件和边界条件，借助Laplace变换及反变换得出一维情况下的无量纲温度、位移及应力的解析解.下文以铜质材料为算例，研究各无量纲量的变化规律，在计算中用到的相关材料参数见表1.

表 1 相关参数Table 1 Related parameters

6.1 磁场的影响

本小节研究磁场对各无量纲温度、位移、应力的影响.取时间t为1，核函数 K(t-ξ) = 1，时间延迟因子ω= 0.01，非局部参数取0，相位迟滞因子均取0.用方程（43）中磁场参数 α= 1+取不同值来体现磁场的变化， α= 1表示磁场为0.磁场取不同值时各无量纲量的分布如图2 ~ 4所示.

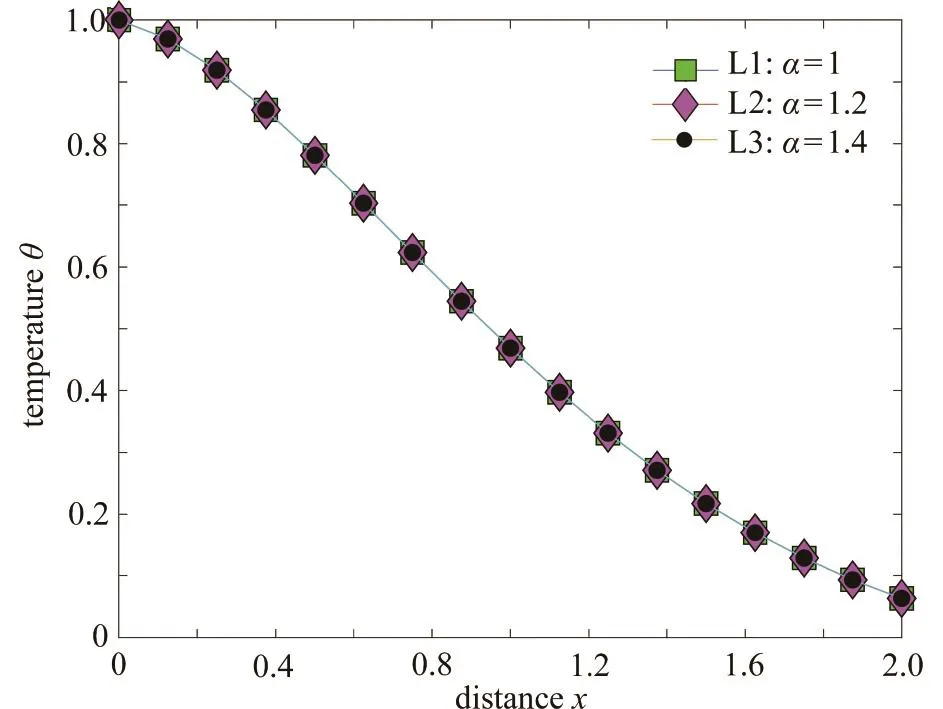
图 2 磁场取不同值时温度θ的变化情况Fig. 2 The variation of temperature θ for different values of the magnetic field

图 3 磁场取不同值时位移u的变化情况Fig. 3 The variation of displacement u for different values of the magnetic field

图 4 磁场取不同值时应力σ的变化情况Fig. 4 The variation of stress σ for different values of the magnetic field

从图2可以看出，随着磁场的增大三条温度分布曲线是重叠的，表明磁场对材料无量纲温度没有影响.图3中随着磁场的增大正位移的峰值逐渐减小，曲线变化趋势趋于平缓，可见磁场的存在对材料的膨胀起到抑制作用.在 x = 1处之后三条曲线开始逐渐趋于重合，可见该处之后的材料面内磁场对位移的影响逐渐消失.从图4可以看出，在 x = 0的边界面上应力始终为0，这与边界条件相一致.在 x = 1处之后的面内，磁场对应力的影响逐渐消失.比较图4中三条曲线可以看出随着磁场的增大，材料内应力峰值一直在减小，即磁场的存在抑制了应力的增大.

6.2 核函数的影响

本小节研究了不同形式核函数对材料无量纲温度、位移、应力的影响情况.时间t取1，磁场参数α取1.2，非局部参数参数取0，相位迟滞因子 τθ，τq均取0，核函数采用式（36）给出的形式.不同核函数下各无量纲量分布如图5 ~ 7所示.

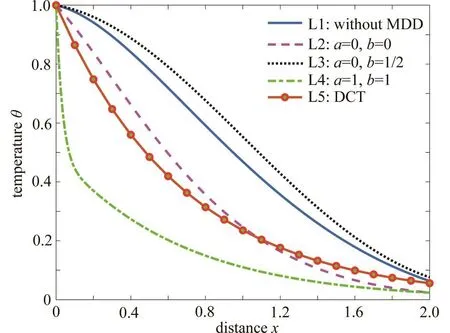
图 5 核函数取不同形式时温度θ的变化情况Fig. 5 The variation of temperature θ for different forms of the kernal function

图 6 核函数取不同形式时位移u的变化情况Fig. 6 The variation of displacement u for different forms of the kernal function

图5中曲线L1 ~ L4时间延迟因子ω取0.01.比较L2、L3、L4可以看出核函数对温度分布的影响主要体现在温度递减速率上.核函数 K(t-ξ) = (1-(t-ξ)/ω)2使得温度曲线下降速度最快，核函数 K(t-ξ) = 1对温度分布影响最小.

曲线L5表示 ω= 0、磁场为0时的温度分布曲线.本文所建立的理论为考虑非局部效应和记忆依赖效应的双相滞后热弹性耦合理论，若 ω= 0则方程（3）退化为Fourier热传导方程，即忽略了记忆效应.本小节非局部因子为0，即忽略了非局部效应.相位迟滞因子 τθ，τq均取0，则方程（7）退化为Biot能量方程（5），即忽略了相位迟滞.由此，本文建立的耦合理论退化成了Biot 经典理论.将曲线L5与国外学者研究结果的图 1[5]做对比，可知分布是合理的.在 x = 0的边界面上温度值始终为1，这与本算例的热边界条件相一致.距离边界面越远处温度越小，这与事实相符.

图6中曲线L2 ~ L4为不同核函数对位移影响的分布曲线.可以看出位移u在边界面处为负值，随着x增大位移先迅速减小至0，而后又逐渐增大，在x=0.4的附近位移u达到正峰值，最后随着x值的增大位移逐渐趋于0.比较曲线L2~L4可得，无论是正位移峰值还是负位移峰值，在核函数 K(t-ξ) = (1-(t-ξ)/ω)2下均为最小，核函数 K(t-ξ) = 1下均为最大.L1表示当 ω= 0、磁场为0时位移u的分布情况，此时模型退化为Biot模型，退化过程与图5相同，所示位移分布与其他学者研究的DCT模型的图 2[5]分布情况一致.

图7为不同核函数下应力的分布情况.曲线L1不考虑记忆依赖效应，曲线L2、L3、L4为三个不同核函数下应力的分布曲线，观察得出核函数对应力峰值的影响与对位移峰值的影响相同.从图7可以看到在x=0处应力为0，在远离边界x=0处应力逐渐趋于0，符合给定的边界条件.

图 7 核函数取不同形式时应力σ的变化情况Fig. 7 The variation of stress σ for different forms of the kernal function

6.3 时间延迟和相位迟滞的影响

本小节研究时间延迟因子和相位迟滞因子对各无量纲量的影响.选取时间t=1，核函数取 K(t-ξ) = 1，非局部因子取0.因热波以有限的速度传播导致热流矢量的传播将滞后于温度梯度的形成，因此热流矢量滞后时间τq大于温度梯度滞后时间 τθ[7].图8 ~ 10为受时间延迟因子和相位迟滞因子影响的各无量纲量分布结果.

图 8 τq ，τθ和ω取不同值时温度θ的变化情况Fig. 8 The variation of temperature θ for different values of τq , τθ andω

图 9 τq ，τθ和ω取不同值时位移u的变化情况Fig. 9 The variation of displacement u for different values of τq , τθ andω

本小节中曲线L1表示时间延迟因子ω取0.01，相位迟滞因子 τq=τθ= 0.曲线L2 ~ L4为ω分别取值0.01， 0.001，0.000 1，相位迟滞因子取值 τq=0.04，τθ=0.02.从图8可以看出，随着时间延迟因子的增大，温度的非0区域沿x轴 减小，这说明热的传播速度是有限的.从图9中可得，时间延迟因子越大， x = 0边界面处由于热量积累时间越少，因此热膨胀程度越弱，负位移越小.但时间延迟因子越大热传播距离越小，受热区域在材料上越集中，因此材料形变越多，正位移峰值增大.从图10可看出时间延迟因子越大应力峰值越大.

图 10 τq ，τθ和ω取不同值时应力σ的变化情况Fig. 10 The variation of stress σ for different values of τq , τθ andω

分别比较三个图中的曲线L1和L2可知相位迟滞的存在加剧了各无量纲量的变化速率，使得介质中温度、位移、应力能更快地趋于平稳.计算中可选取不同的时间延迟因子和相位迟滞因子组合计算以满足实际需要.

6.4 非局部的影响

本小节研究非局部效应对无量纲温度、位移、应力的影响.取核函数 K(t-ξ) = 1，时间延迟因子 ω= 0.000 1，相位迟滞因子 τq=τθ= 0.非局部因子 e0a分别取0，0.05，0.1，非局部因子取不同值时各无量纲量的分布情况如图11 ~ 13所示.

图 11 e0a 取不同值时温度θ的变化情况Fig. 11 The variation of temperature θ for different values ofe0a

图 12 e0a 取不同值时位移u的变化情况Fig. 12 The variation of displacement u for different values ofe0a

从图11看出所得三条无量纲温度分布曲线几乎重合，即非局部因子对无量纲温度分布几乎无影响.从图12看出随着非局部因子的增大，正位移峰值减小，负位移峰值几乎无变化.从图13看出随着非局部因子的增大，应力峰值减小.从本小节可以看出，非局部参数越大，其对材料的位移、应力影响越明显，这表明微尺度材料尤其纳米材料，在工程中考虑非局部的影响具有重要意义.

6.5 时间的影响

本小节研究无量纲温度、位移、应力随时间变化的分布图.取核函数 K(t-ξ) = 1，时间延迟因子 ω= 0.000 1，相位迟滞因子 τq=τθ= 0，非局部因子取0.不同时刻各无量纲量的分布情况如图14 ~ 16所示.

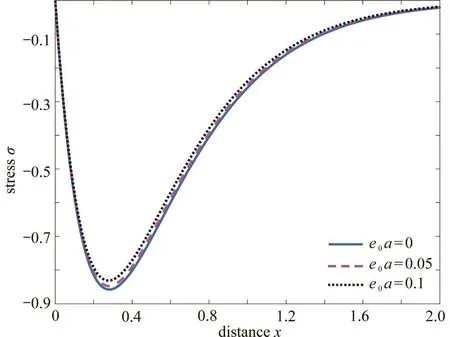
图 13 e0a 取不同值时应力σ的变化情况Fig. 13 The variation of stress σ for different values ofe0a

图 14 t取不同值时温度θ的变化情况Fig. 14 The variation of temperature θ for different values of t

图 15 t取不同值时位移u的变化情况Fig. 15 The variation of displacement u for different values of t

图 16 t取不同值时应力σ的变化情况Fig. 16 The variation of stress σ for different values of t

为研究各无量纲随时间变化的分布图，需要将变化热源固定，即用控制变量的方法固定边界条件，从而使时间成为唯一变量.因此，本小节热边界条件采用 θ(0,t) = 1[7].

从图14可以看出，从x轴分布情况来看，无量纲温度的非0区域是有限的，这说明热传播速度是有限的.当 t = 0.1和 t = 0.05时，温度曲线各自存在一个骤降的区域，即温度快速降为0，温度骤降位置便是热波前位置.随着时间t的增大，温度骤降现象消失，且无量纲温度的非0值区域一直在增大，即热扰动区域一直增大.

从图15可看出，在 x = 0边界面处发生了热膨胀，位移为负值.从x轴 分布情况来看，随着x增 大位移一直减小到0，之后介质因受热而收缩，位移为正并逐渐达到峰值.最后位移减小并趋于0.

从图16可看出，在 x = 0边界面处应力始终为0，从x 轴分布情况来看，随着x增 大材料内压应力先迅速增大，之后较缓慢减小至0.当时间越小时，应力变化速率越大，介质中应力区域愈集中，且时间越小应力峰值越大.

6.6 Laplace反变换算法的影响

本小节研究反变换过程中自由设置的参数对反变换结果的影响.参数设置对反变换结果的影响是一个纯粹的数学问题，因此本小节以式（49）为例，对该式进行不同参数的数值反演以说明反变换过程中参数设置的作用.

本文基于Brancik的程序编写了Laplace反变换程序，相对误差 Er控制在1 0-11内[26].程序的核心思想是快速Fourier变换和“ε-algorithm”，其中“ε-algorithm”是一种迭代算法，迭代控制参数P和M可自由设置.P为正整数，通常设置为2或3，M为2的幂[25].P值的作用：决定“ε-algorithm”迭代算法的最终结果，当设定其取值，迭代计算的最终结果值为，迭代过程见文献[25]的图1.M值的作用：若用 tm表示计算设定的最大时间，则M是时间间隔 t∈(0,tm)内计算点的数量.取 ω= 0.000 1， τq=τθ= 0， e0a = 0， K(t-ξ) = 1，不同P值和M值对式（49）反变换结果的影响如图17、图18所示.

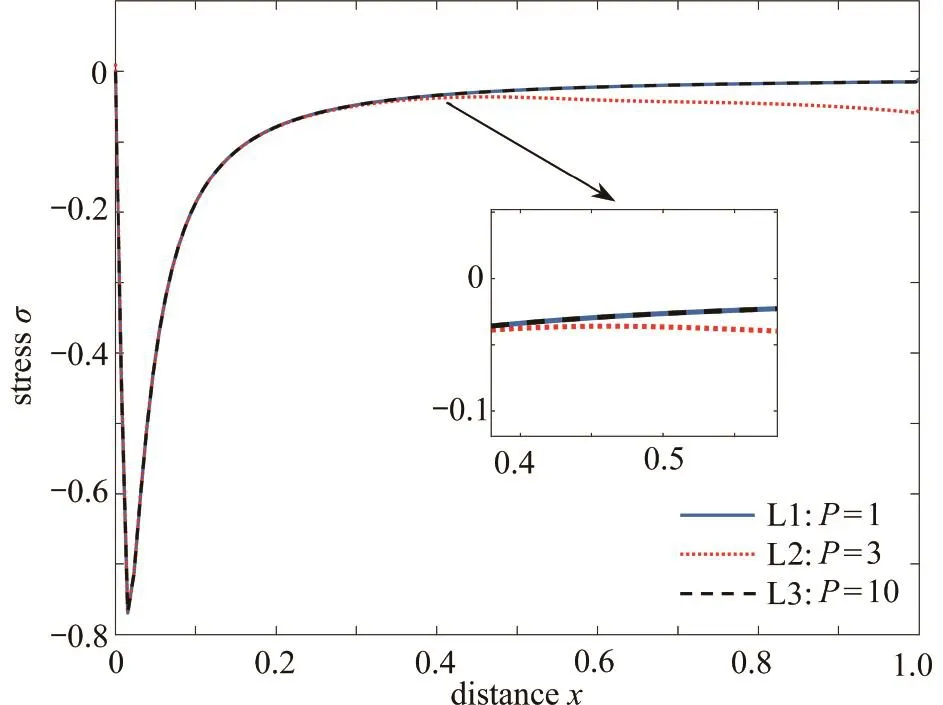
图 17 P取不同值时应力σ的变化情况Fig. 17 The variation of stress σ for different values of P

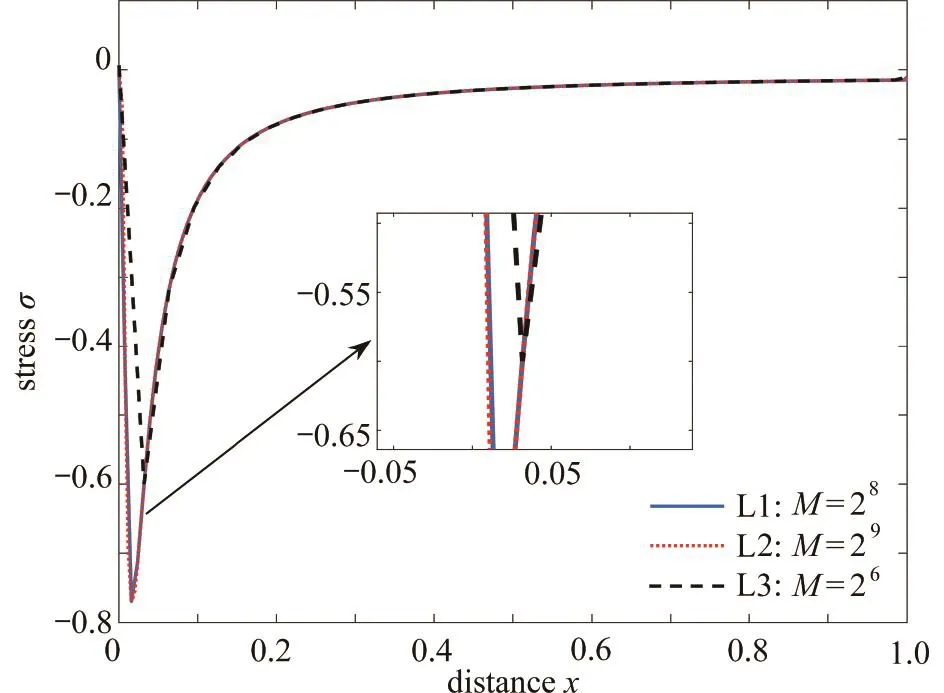
图 18 M取不同值时应力σ的变化情况Fig. 18 The variation of stress σ for different values of M

图17中L2为P取经验值3时的反变换结果，其结果在相对误差以内.而当P取值较大时，在 x = 0.4之后其反变换误差随x增大而增大，这与Brancik的研究结果相似.当P取1时对本例几乎无影响.图18中L1和L2分别为M取256和512的反变换结果，可以看出计算点多于经验值256后，反变换结果并没有变化.由此可见计算点太多不仅不能提高计算精度，还增加了计算机的计算时长.但是当M值取64时，由于计算点数目太少，在σ变化较大的区域计算误差非常大，在σ变化较小的平缓区域计算误差相对较小.

7 结 论

本文基于双相滞后广义热弹性理论，同时考虑记忆依赖效应和非局部效应，研究了窄长薄板受到磁-热弹耦合作用下的动态响应问题.通过分析得出以下结论：

1）核函数的形式、时间延迟因子和相位迟滞因子对各无量纲量有明显的影响.根据工程需要，选取不同的核函数、时间延迟因子和相位滞后时间的组合作为新指标来计算，可更精确地表征材料的力学行为.

2）时间延迟因子对各无量纲量有明显的影响，随着时间延迟因子的增大，温度非0区域减小，正位移和应力的峰值均增大.

3）相位迟滞加剧了各无量纲量的变化速率，使介质内温度、位移、应力更快趋于平稳.

4）非局部因子对无量纲温度分布几乎无影响，但对位移、应力峰值有明显的影响.随着非局部参数的增大，正位移和应力的峰值均减小.

5）磁场对无量纲温度的分布无影响.正位移和应力的峰值随着磁场的增大在减小.可见磁场的存在对材料的位移、应力变化起到抑制作用.

6）在给定的时刻下，各无量纲量的非0值都分布在有限的区域内，这反映出热传播速度是有限的.当时间尺度非常小时，无量纲温度在热波波前位置骤降趋于0.当时间增大时，正位移的峰值和边界面处负位移的绝对值均增加，应力的峰值减小.

7）在Laplace反变换过程中设置恰当的参数对反变换结果的准确性影响很大.