空间机器人组装超大型结构的动力学分析*

王启生， 蒋建平， 李庆军， 江国期， 邓子辰

（1. 中山大学 航空航天学院，广州 510000；2. 西北工业大学 工程力学系，西安 710072）

引 言

超大型航天器一般是指结构尺寸达千米量级的航天器，在空间能源开发、宇宙奥秘探索、地面军事侦察等领域具有重要应用[1].超大型航天器的结构尺寸已经远远超出火箭整流罩的范围，难以采用一次发射入轨、在轨展开的方式进行建造[2].因此，模块化设计制造、多次发射入轨、机器人在轨组装成为建造超大型航天器的有效途径[3-4].

动力学与控制问题是超大型航天器在轨组装的基础科学问题，得到了广泛关注.王恩美等[5]针对超大型结构在轨组装时构型逐渐增大的过程，提出了面向结构主动控制的动力学建模方法，采用“节点自由度加载”方法和邻接矩阵描述构型渐增引起的模型更新.Cao等[6]针对空间太阳能电站的球形太阳能电池阵列在轨组装问题，采用相对轨道方程和弹性梁有限元建立了组装系统的动力学方程，研究了万有引力梯度引起的结构动力学响应，并基于动力学响应提出了组装策略.Wang等[7]建立了空间太阳能电站在轨组装过程的结构动力学模型，研究了组装过程引起的结构振动，并提出了分布式结构振动控制方法.荣吉利等[8]采用自然坐标法与绝对节点坐标法对空间太阳能电站的刚性与柔性构件建立了动力学模型，研究了组装时间、组装机构的阻尼和刚度系数对组装过程的影响.但是文献[5-8]只关注了超大型结构的动力学行为，没有考虑空间机器人的操作过程的动力学建模与仿真、轨迹规划、控制策略等问题.

机器人组装超大型航天器过程中，需要对大型组装模块进行多种操控，例如抓捕、搬运、调姿、安装等，这些操控的精准实现是组装任务顺利完成的前提.Chen等[9]研究了多个刚柔耦合航天器自主、协调在轨组装问题，基于输出一致控制器和避撞控制器提出了一种复合控制方法，完成装配任务的同时，能有效避免航天器之间的碰撞、抑制挠性附件的振动.周志成等[10]针对柔性机器人抓捕大型航天器后组成的系统，采用假设模态法和有限元法进行了系统动力学建模，提出了一种组装过程轨迹跟踪的控制方法，有效抑制了柔性部件的结构振动.朱安和陈力[11]研究了空间双臂机器人捕获目标航天器后的避撞柔顺控制问题，设计了关节柔顺机构，基于神经网络提出了混合体系统姿态稳定的全阶终端滑膜避撞柔顺控制方法.Xu等[12-13]针对带柔性附件的空间机器人抓捕带柔性附件的航天器的过程，研究了系统的动力学建模、机械臂的轨迹规划以及关节跟踪控制问题，实现了机械臂末端轨迹跟踪的同时抑制了柔性附件的结构振动.Lu等[14]对基于视觉测量的空间机器人在轨组装技术和控制策略进行了地面实验验证.Dubowsky和Boning[15]对空间机器人群体组装大型空间结构过程进行了协调控制器设计和地面实验验证研究，实现了机器人控制和结构振动控制的解耦.

由于超大型结构具有超大尺寸和超大柔性的特点，在轨组装时，如果空间机器人操作不当很容易引起结构的横向运动与低频结构振动，降低组装的精度和效率，甚至影响组装任务的成败.因此，空间机器人在轨组装超大型结构时，必须尽可能避免横向运动与结构振动，这对空间机器人的轨迹规划和控制方法提出了较高的要求.然而，文献[5-8]主要研究超大型航天器组装过程的动力学与控制问题，没有考虑空间机器人进行超大型模块安装过程的动力学与控制问题.文献[9-10, 12-15]主要关注机器人的操控和小型柔性附件的结构振动抑制，而非避免横向运动与结构振动的操控方法.为此，本文从轨迹规划和控制的角度出发，研究空间机器人组装超大型结构过程中避免横向运动与结构振动的方法.

空间机器人组装超大型结构的过程可分为四个阶段：抓捕阶段、位姿调整与稳定阶段、安装阶段、爬行阶段.本文针对安装阶段，进行了动力学建模、轨迹规划、轨迹跟踪控制三方面的研究，最后给出了系统参数对组装过程的影响.

1 动力学建模

本节首先给出二维刚体动力学建模的自然坐标法，然后采用自然坐标法和绝对节点坐标法建立机器人-主结构-待组装结构系统的刚柔耦合动力学模型.

1.1 系统描述

组装系统包括双臂机器人、主结构、待组装结构三部分，如图1所示.本文主要关注共线安装的轨迹规划与控制效果，只研究系统的平面运动.图1中的4表示机器人本体，1~3和5~7表示机械臂，点B~G为机械臂关节点，MN为主结构，KI为待组装结构.假设机器人已经抓捕了主结构和待组装结构，即点A与点N重合，点H与点K重合.组装过程中，主结构和待组装结构在空间机器人的控制下相互靠近，直至最终点N与点K重合.组装过程相对于轨道周期而言时间较短，因此可忽略万有引力及空间摄动力的影响[16].

图 1 组装系统示意图Fig. 1 Schematic diagram of the assembly system

主结构和待组装结构简化为Euler-Bernoulli梁，机器人简化为多刚体系统，忽略关节的摩擦等非线性因素.空间组装机器人的几何和质量参数参考加拿大臂2的参数[17]，如表1所示，刚体1~7的长度和质量分别用和表示.主结构和待组装结构都由若干个基本组装模块组成.根据文献[4]，基本组装模块的参数如表2所示.

表 1 刚体机械臂的参数Table 1 Parameters of the rigid manipulator

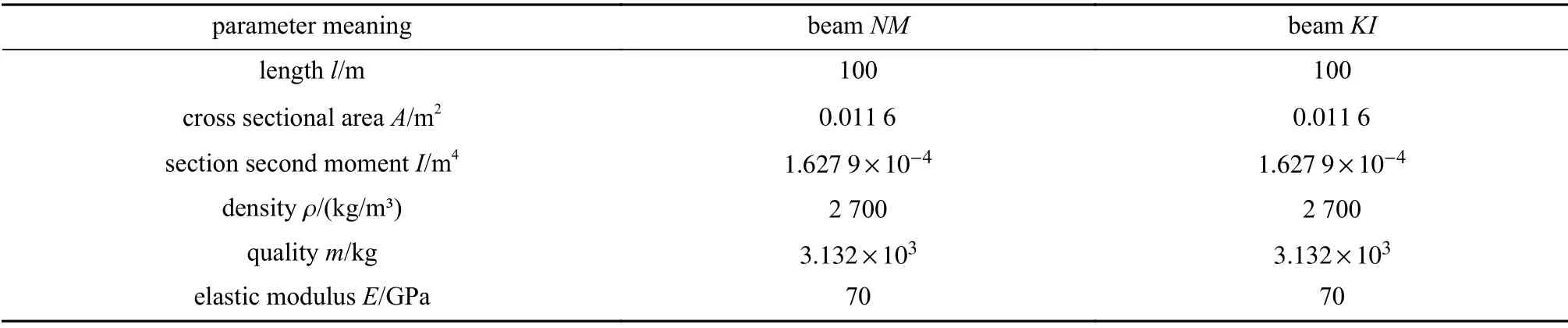
表 2 基本组装模块的参数Table 2 Parameters of the basic assembly module

1.2 自然坐标法与绝对节点坐标法

一个平面刚体只有3 个自由度，而方程(1) 有6 个广义坐标，所以这些坐标必然受到3 个刚体内部约束：

图 2 刚体AB的自然坐标描述Fig. 2 The natural coordinate description of rigid body AB

以点A为局部坐标系原点，以 (rB-rA)/l1和v1为局部坐标系的基矢量，构建刚体的局部坐标系ξ Aη，如图2所示.刚体上任意一点在全局坐标系下的位置矢量可以表示为

其中， C = [(1-ξ/l1)I2(ξ/l1)I2ηI2]为刚体的形函数，ξ，η为该点在局部坐标系 ξAη的坐标，I2为单位矩阵.

刚体内任意一点的速度为

则刚体的动能可表示为

其中，V 为刚体的体积， MAB为刚体AB的质量矩阵.由于不考虑刚体的万有引力及空间摄动力，所以刚体的势能为零.因此，对于单个刚体组成的动力学系统，动力学方程为

其中， pAB为刚体AB的广义动量， fAB为广义力向量， λAB为Lagrange乘子向量.

主结构NM和待组装结构KI均采用绝对节点坐标法进行建模，采用一维二节点Euler-Bernoulli梁单元进行离散[18].该绝对节点坐标法单元的广义坐标为

广义坐标的具体定义为

其中，xe为单元内的局部坐标，le为单元的长度.单元内任意一点的全局坐标可通过以下插值得到：

形函数 S(xe)的表达式为

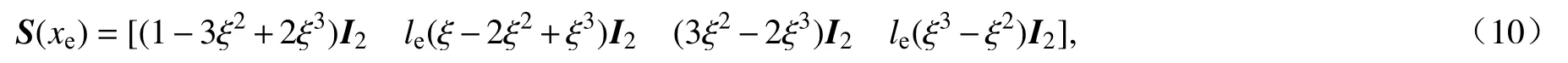
其中， ξ= xe/le.绝对节点坐标法单元的质量矩阵与弹性力表达式见文献[18]，弹性力中考虑了梁的轴向拉压变形与弯曲变形，且能够描述大变形的几何非线性现象.

1.3 系统的刚柔耦合动力学模型

空间机器人由7个刚体构成，共有42个广义坐标，21个刚体内的内部约束，12个刚体间的约束（描述点B，C，D，E，F，G处不同刚体的坐标重合），共33个约束.为了简化建模过程，刚体共用点的坐标不重复选取，即可减少12个广义坐标和12个约束.整个空间机器人的广义坐标为

空间机器人的约束为

其中 ri1和 ri2为刚体i 的两个节点的位置矢量.方程(12)也可以缩写成

梁NM、梁KI均采用绝对节点坐标法的一维二节点Euler-Bernoulli梁单元进行动力学建模[19]，每个节点有4个自由度.基于这种单元，系统的广义坐标为

其中， qNM∈R4×nNM+ 4和 qKI∈R4×nKI+ 4分别代表梁NM和梁KI的广义坐标， nNM和 nKI分别为梁NM和梁KI的单元数.

为了描述空间机器人与主结构/待组装结构的夹持行为，本文参考文献[20]，将夹持连接简化成x， y 方向的直线弹簧-阻尼系统和扭转弹簧-阻尼系统.因此，空间机器人上的刚体AB在点A处所受的夹持力和力矩分别为

其中， vNM表示梁在点N处的切线矢量，可通过 qNM的第3、4个广义坐标的单位化得到.为简化起见，不再给出刚体GH、梁NM、梁KI所受的夹持力和力矩表达式.由于夹持力和力矩不是本文的研究重点，在数值仿真中取 k = 106和 c = 103即可达到较高的夹持精度，使夹持对组装精度产生的影响可以忽略不计.

系统的Hamilton方程最终表示为以下形式：

其中，M为系统质量矩阵，p为系统广义动量，λ为Lagrange乘子向量，f 为广义力向量（包括梁的弹性力、弹簧回复力、阻尼力、控制力等）.绝对节点坐标单元的弹性力中包含了弯曲变形和轴向拉压变形引起的弹性力，考虑了几何非线性的作用，是广义坐标的强非线性函数，广义弹性力的表达式见文献[19].质量矩阵M和广义力向量f 可通过刚体/柔性体的质量矩阵和广义力向量叠加得到.

2 组装过程轨迹规划与控制

机器人完成主结构和待组装结构的抓捕后，一般情况下主结构和待组装结构并不共线.由于主结构和待组装结构都具有超大、超柔的特点，此时并不适于直接组装，否则组装过程可能引起较大的结构振动，给组装对接口的对准带来困难，对组装精度造成较大影响，甚至影响组装的成败.因此，抓捕后必须先进行主结构和待组装结构的位姿调整，等位姿稳定后再进行主结构和待组装结构的安装操作.因此，本文将组装过程分为抓捕阶段、位姿调整与稳定阶段、安装阶段和爬行阶段.受篇幅所限，本文仅针对安装过程进行研究，提出了一种共线安装的轨迹规划与控制方法.

2.1 共线安装轨迹规划

在安装阶段，为了避免安装过程引起主结构和待组装结构的振动，提出一种共线安装方法，要求机器人的质心在Y轴方向始终保持不变.为了描述共线安装的轨迹，将空间机器人初始放置于图3所示的位置，点A与点O重合，X轴指向点H，Y轴指向点B.共线安装的轨迹需要满足以下三方面的要求：① 机械臂AB和GH在组装过程中保持垂直于X轴，且AH始终平行于X轴，从而保证空间机器人不会引起主结构和待组装结构的转动.② 点A和点H之间的距离采用5次多项式进行规划，从而满足初末时刻的速度和加速度要求.③ 点A和点H的Y坐标保持不变，从而避免空间机器人对主结构和待组装结构施加Y方向的力.

图 3 机械臂正运动学坐标系Fig. 3 The forward kinematics coordinate system of the manipulator

如果空间机器人在安装阶段始终保持对称构型，则要求①可以得到满足，且有以下几何关系：

为了满足要求②，点A和点H之间的距离 XAH通过5次多项式进行规划，即

假设主结构和待组装结构对接锁定时不需要相对速度，因此初末时刻的相对速度和加速度均为0，则有

其中t3为安装阶段的时间长度.通过上述公式，可规划出 XAH随时间的变化规律.为了实现该运动，需要将直角坐标下的轨迹转化为机械臂关节角度随时间的变化，实现关节空间的轨迹规划.根据几何关系有

空间机器人质心到直线AH的距离Yc的表达式为

由于组装系统不受外力的干扰，所以空间机器人的质心在惯性坐标系 XOY 保持不变，因此为了满足要求③，要求 Yc是一个常数.给定 XAH0，即可得到 XAH(t)，再结合 Yc，通过求解方程(22)和方程(23)的非线性方程组，得到θ1和 θ2随时间的变化规律，再通过式(19)即可得到 θ3~ θ7随时间的变化规律，实现共线安装的轨迹规划.

在本文的数值仿真中，假设安装阶段的时间为 t3= 300 s ，给定 XAH= 18 m， Yc= 8 m，从而得到安装阶段的轨迹规划结果，如图4所示（θ4始终为0，θ5，θ6，θ7分别与 θ3，θ2，θ1重合）.由图可知，整个安装阶段中各关节的规划角度随时间平滑变化，在安装阶段的末时刻，关节角速度为0，避免主结构和待组装结构的碰撞.

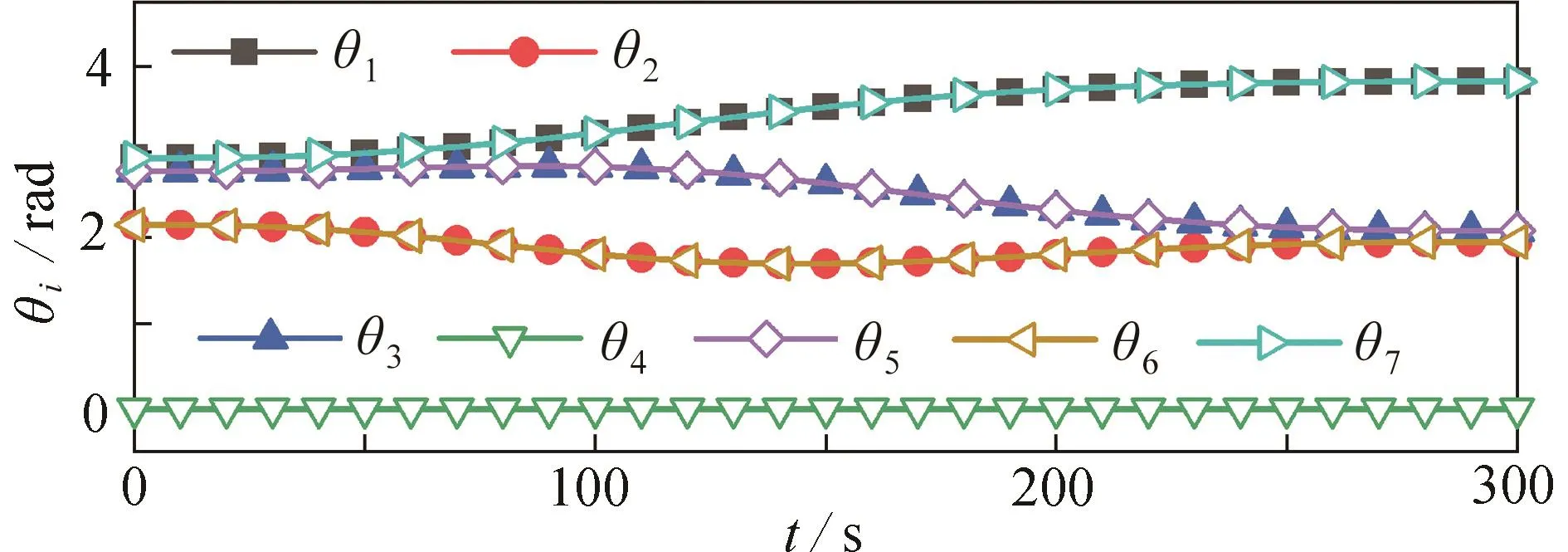
图 4 安装阶段关节角度规划结果Fig. 4 Joint angle planning results during the whole assembly process

2.2 非共线安装轨迹规划

本小节给出一种非共线安装的轨迹规划方法作为对比，安装过程中机器人的质心位置不作要求.采用直线AH到直线DE的距离 YAD保持不变的方法进行轨迹规划，因此需要将方程(23)改成如下方程：

通过求解方程(22)和方程(24)的非线性方程组，得到 θ1和 θ2随时间的变化规律.本文给定 YAD= 12 m.

2.3 控制器设计

采用PD控制方法对空间机器人进行控制，控制力矩的表达式为

其中ei为控制误差， Kpi和 Kdi分别为比例和微分增益，为ei对时间的导数，在数值仿真中可通过差分近似代替.控制力矩 Mi的正方向定义为ei增大的方向，通过虚功原理可得到控制力矩的广义力向量.误差的定义为

其中下标“p”代表轨迹规划的结果，θi在数值仿真中可通过广义坐标的反三角函数计算得到.比例和微分增益分别取为

3 仿 真 分 析

本节对安装阶段进行数值仿真分析，给出共线安装和非共线安装的仿真结果.时间步长为0.000 2 s，主结构和待组装结构都由1个基本组装模块组成，即主结构和待组装结构的长度均为100 m.

3.1 共线安装方法

对于安装阶段，图5 ~ 9给出了共线安装轨迹规划方法得到的数值仿真结果.由图5可知，主结构和待组装结构沿安装方向的运动过程比较平滑，两者均匀地向 X = 9处靠近，符合动量守恒定律，最后相对速度几乎为零，避免了相互碰撞.图6给出了 e1~ e4随时间的变化情况，由于 e5，e6，e7分别与 e3，e2，e1重合，为简化起见，没有给出 e5，e6，e7的曲线.控制误差不超过0.0002 rad，且 e4恒为零，控制结果较好地跟踪了轨迹规划的结果.从轨迹规划和控制误差的对称性可以看出，组装过程中，空间机器人一直保持对称构型，这是由于主结构和待组装结构都由1个基本组装模块组成，质量参数相同.图7给出了控制力矩随时间的变化，由于在安装过程中机械臂5、6、7与机械臂3、2、1分别保持对称构型，因此 M5， M6， M7分别与 M3， M2， M1重合，为清晰起见，图中没有给出 M5， M6，M7的曲线.M1的最大值为3.805 N·m， M2的最大值为14.830 N·m，M3的最大值为28.175 N·m， M4恒为零.

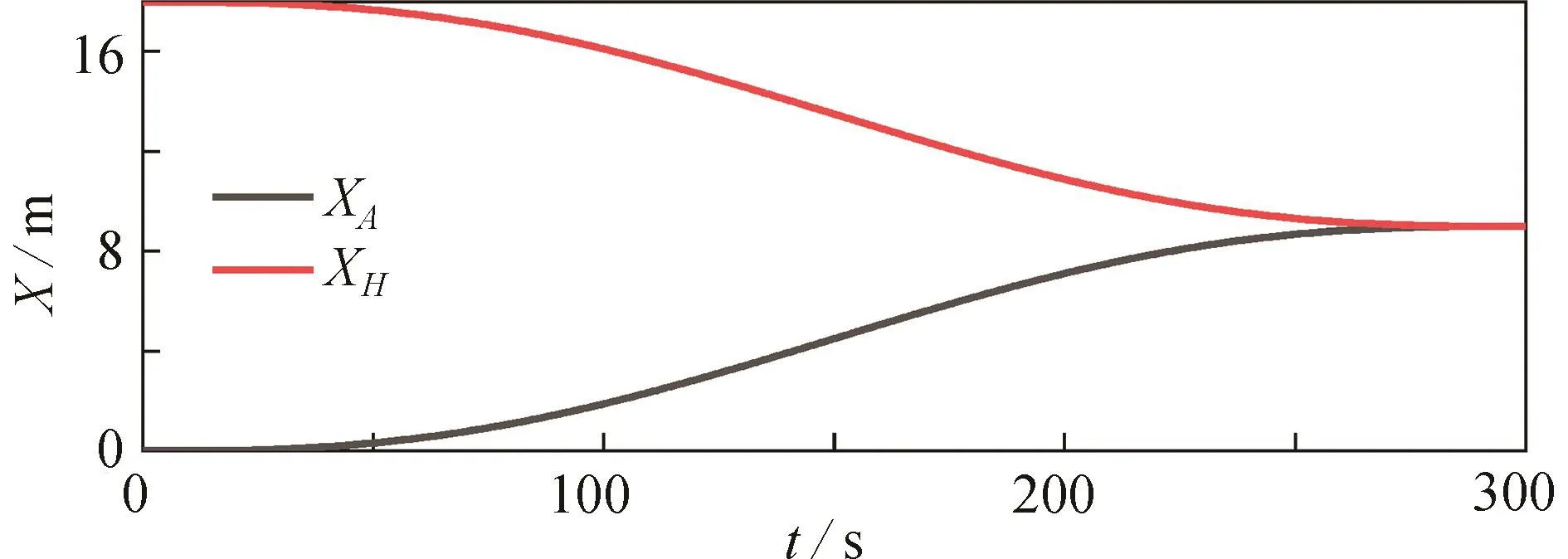
图 5 主结构和待组装结构在组装方向的运动（共线安装）Fig. 5 Movement of the main structure and the structure to be assembled in the assembly direction (collinear assembly)

图 6 空间机器人控制误差（共线安装）Fig. 6 Control errors of the space robot (collinear assembly)

图 7 空间机器人控制力矩（共线安装）Fig. 7 Control torques of the space robot (collinear assembly)

图8给出了点A和点H的Y方向位移，图9给出了主结构和待组装结构的转动，图9中下标1、2分别代表主结构和待组装结构，后同.由图可知，主结构和待组装结构在Y方向的位移小于1.5 mm，转动小于，相比于100 m的结构尺寸可以忽略不计，基本实现了共线安装.因此，本文提出的共线安装轨迹规划方法和轨迹跟踪控制算法能有效避免安装操作引起的主结构和待组装结构的振动.

3.2 非共线安装方法

图10和图11给出了非共线安装的数值仿真结果.由图可知，主结构和待组装结构在夹持点处出现了0.3 m左右的Y方向位移和大约 3×10-5rad的转动.图12给出了两种安装方法主结构点A夹持力矩的变化情况.容易看出，共线安装方法下最大夹持力矩为1.53 N·m，非共线安装最大夹持力矩为9.05 N·m，达到了共线安装的6倍左右.非共线安装需要较大的夹持力矩，是因为主结构和待组装结构出现了Y方向的位移，需要Y方向的夹持力和夹持力矩共同抵消惯性力的影响.图13给出了共线安装方法和非共线安装方法的安装过程，从图中可以明显看出，由于空间机器人构型改变，非共线安装的主结构和待组装结构出现了Y方向的位移；而共线安装方法通过各关节的紧密配合，保证了主结构和待组装结构在Y方向几乎没有位移.

图 8 主结构和待组装结构在夹持点处的 Y 方向位移（共线安装）Fig. 8 Y-direction displacements of the main structure and the structure to be assembled at the grasping point (collinear assembly)

图 9 主结构和待组装结构在夹持点处的转动（共线安装）Fig. 9 Rotations of the main structure and the structure to be assembled at the grasping point (collinear assembly)

图 10 主结构和待组装结构在夹持点处的 Y 方向位移（非共线安装）Fig. 10 Y-direction displacements of the main structure and the structure to be assembled at the grasping point (noncollinear assembly)

从上述分析可以看出，共线安装方法引起的主结构和待组装结构的Y方向运动更小，所需的夹持力矩也更小，因而有利于提高安装精度、避免结构振动.因此，在本文的后续研究中，都采用共线安装的轨迹规划方法.

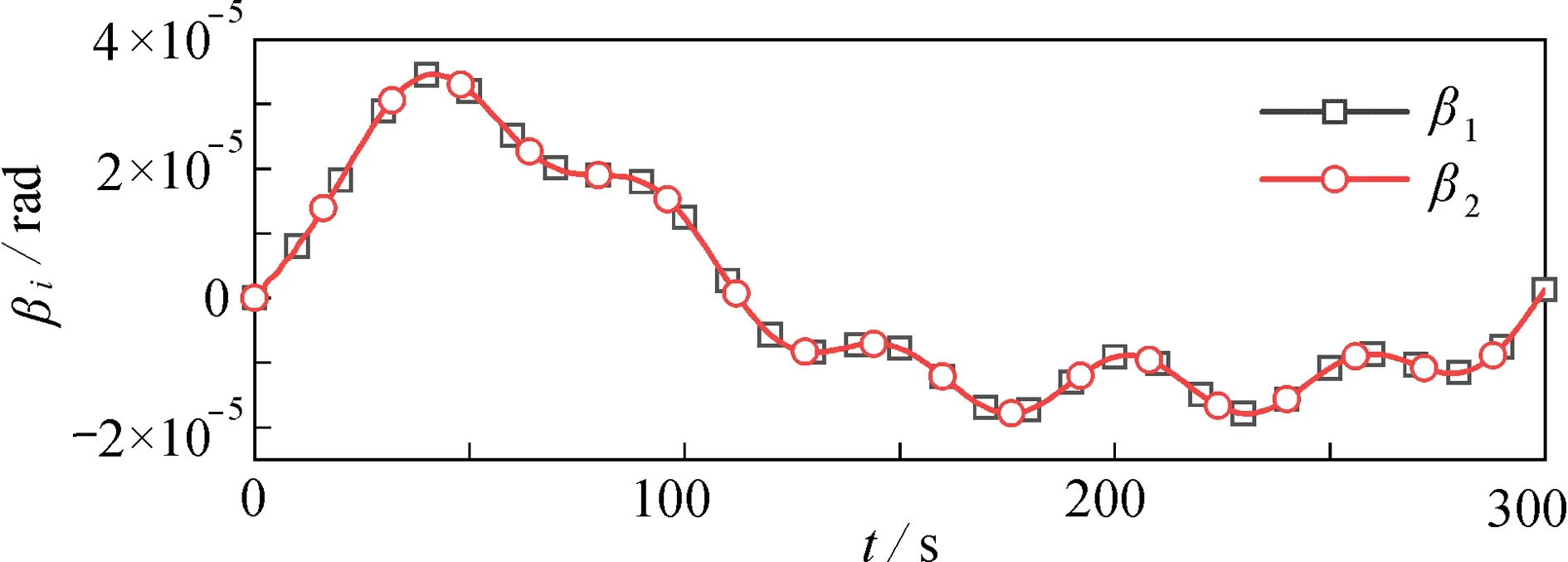
图 11 主结构和待组装结构在夹持点处的转动（非共线安装）Fig. 11 Rotations of the main structure and the structure to be assembled at the grasping point (noncollinear assembly)

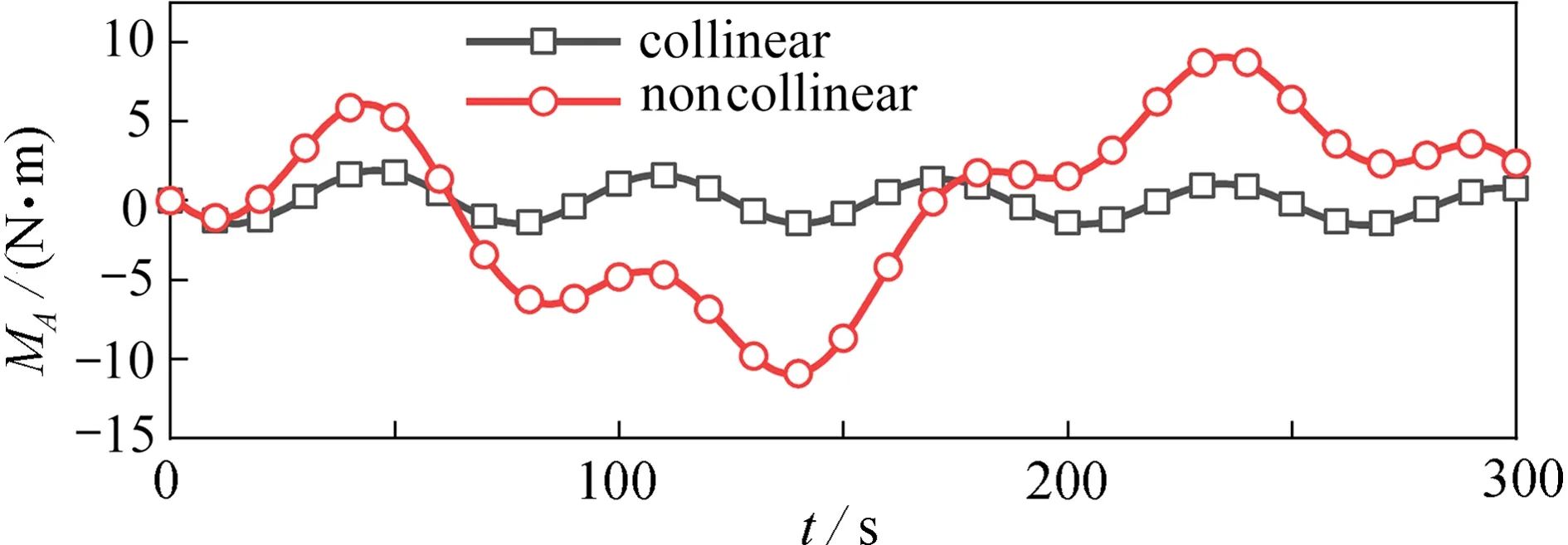
图 12 点A处的夹持力矩Fig. 12 Grasping moments at point A

图 13 两种安装方法比较Fig. 13 Comparison of 2 assembly methods

4 系统参数对安装过程的影响

令 n1和 n2分别代表主结构和待组装结构的基本组装模块数.超大型结构的组装过程中可能会出现多种n1和 n2的组合，本节研究 n1和 n2对共线安装过程的影响，为组装方案设计提供参考.

4.1 基本组装模块数量同步增加的影响

令基本组装模块数相等（n1= n2），取值从1到10变化，数值仿真结果如图14 ~ 16所示.由图可见，基本组装模块数量越多，控制误差和控制力矩越大.基本组装模块数量为1，2，4时，对应的最大控制力矩分别约为28.17 N·m，53.28 N·m，134.59 N·m.图16给出了组装过程中 M3的最大值 M3,max随基本组装模块数的变化情况，由图可知，最大控制力矩随基本组装模块数线性增长.由于空间机器人的关节最大输出力矩有限，当模块数量增加时应适当延长组装时间，避免了过大的关节力矩.

图 14 基本组装模块数量同步增加对控制误差的影响Fig. 14 The influence of synchronous increases of the numbers of basic assembly modules on the control errors

图 15 基本组装模块数量同步增加对控制力矩的影响Fig. 15 The influence of synchronous increases of the numbers of basic assembly modules on the control torques

图 16 基本组装模块数量同步增加对 M3,max 的影响Fig. 16 The influence of synchronous increases of the numbers of basic assembly modules onM3,max

图 17 基本组装模块数量不同步增加对控制误差e 3的影响Fig. 17 The influence of unsynchronized increases of the numbers of basic assembly modules on control errore3

4.2 基本组装模块数量不同步增加的影响

令待组装结构的基本组装模块数量 n2始终为1，主结构的基本组装模块数量 n1从1到10变化，仿真结果如图17 ~ 20所示.由图可知，随着 n1增加，最大控制力矩和最大误差也明显增大，但是增大的程度比 n1，n2同时增加时慢.当 n1，n2均为1时，控制力矩 M4=0，但是随着 n1增加，控制力矩 M4不再为0.这是因为空间机器人两端夹持物体的质量不同，根据动量守恒定理，质量大的主结构在组装过程中移动距离短，质量小的待组装结构移动距离大，使得空间机器人出现了X方向的移动；而由于主结构和待组装模块对空间机器人的力并不经过质心，所以空间机器人沿X方向移动的同时也会出现转动，因此需要控制力矩 M4维持空间机器人不出现转动.

图 18 基本组装模块数量不同步增加对控制力矩 M3的影响Fig. 18 The influence of unsynchronized increases of the numbers of basic assembly modules on control torqueM3

图 19 基本组装模块数量不同步增加对控制力矩的影响Fig. 19 The influence of unsynchronized increases of the numbers of basic assembly modules on control torqueM4

图 20 基本组装模块数量不同步增加对 M3,max ， M4,max 的影响Fig. 20 The influence of unsynchronized increases of the numbers of basic assembly modules on M 3,max， M4,max

5 结 论

本文从动力学建模、轨迹规划、轨迹跟踪控制和数值仿真四个方面对空间机器人组装超大型结构的过程进行了研究，提出了共线安装的轨迹规划方法.研究发现：与非共线安装方法对比，共线安装的轨迹规划方法通过对空间机器人质心的规划，可最大程度避免引起主结构/待组装结构的横向运动，且所需的夹持力矩更小，有利于提高组装精度，符合超大、超柔航天器的在轨组装需求.当主结构和待组装结构的基本模块数相同时，空间机器人的构型、控制误差和控制力矩具有对称性，空间机器人本体不发生转动；当主结构和待组装结构的基本组装模块数量不相同时，空间机器人在组装过程中质心在组装方向发生移动，同时还会出现小幅转动，因此需要对空间机器人本体实施姿态控制.