多目标支持向量机及其在少样本故障诊断中的应用①
2022-09-20江勋林
江勋林
(陆军步兵学院, 南昌 330103)
1 引言
柴油机是一个复杂的系统, 其故障往往表现为多故障的强关联耦合, 是机械故障诊断的技术难题[1].正是由于这种强关联耦合, 表现为故障征兆的不确定性, 采用传统的人工诊断或者一般的专家系统进行诊断, 往往效率不高而且出现误判的概率较高. 人工神经网络方法(ANN)和支持向量机(SVM)方法等智能诊断方法能较好地处理征兆与故障之间的复杂映射关系,更适合于多故障强关联耦合的柴油机故障诊断问题[2,3].其中人工神经网络可以构建出更复杂的映射关系, 却需要更充分的训练, 当样本量少时会出“欠学习”现象,往往应用于大数据量的情况[4]. 在少样本问题识别上,支持向量机在模型复杂度和学习能力上表现出更好的综合性能, 效率更高, 泛化能力更强[5,6].
支持向量机理论简单, 实用性很强, 被大量应用于模式识别问题中[7]. 然而, 支持向量机分类效果与其核函数参数的选择存在强烈的关系, 不恰当的参数极可能导致不同的分类结果[8]. 采用启发式优化方法可以很好地提升支持向量机的分类性能[9]. 粒子群(PSO)算法是一种典型的启发式智能搜索算法, 经过多年的发展, 具有较好的全局寻优能力, 适合于支持向量机参数优化这种多峰问题[10].
支持向量机本质上是通过核特征空间的非线性映射, 将低维的非线性特征映射为高维的线性特征. 然而这种复杂映射难于实现人们对分类的真正期望. 因此,只是将支持向量机的等效间隔距离作为目标是不够的,而是应该从等效间隔距离、样本分类误差等多个方面同时寻优[11]. 多目标优化问题的求解需要采用多目标优化算法进行求解, 常用的多目标优化算法有MOPSO、NSGA-II、NPGA等[12]. 其中多目标粒子群优化(MOPSO)是一种采用粒子群解决多目标优化问题的非常经典的算法[13]. 该算法具有较高的收敛速率, 且能够保证解分布的均匀性和宽广性, 从而保证了最终解的多样性, 是最常用于求解多目标问题的算法.
本文在分析支持向量机参数优化对结果影响的基础上, 选取负等效间隔距离、支持向量的数量、样本的错分率作为分类器的3个目标, 提出一种基于粒子群的多目标支持向量机, 并将其应用于少样本的柴油机异响故障诊断问题中.
2 支持向量机的参数及目标
2.1 参数对分类结果的影响
支持向量机不同的参数所获得的最优超平面大不相同. 如图1所示, 该图为一个三分类问题, 3个类别的数据以各自中心随机分布的样本. 在分类时都采用的是高斯径向基核函数, 两者采用的规则化参数C分别为800和500, 而两者采用的径向基函数系统方差δ分别为1和0.1. 其中, 图中圈出来的样本点为支持向量,底色表示最终分类的结果.

图1 不同参数的分类结果
图1显示, 当参数取C=800, δ=1时, 支持向量较少, 而且支持向量主要集中在两个类别的边界附近, 分类边界近似为直线; 当参数取C=500, δ=0.1时, 支持向量较多, 分布于每种类别的外圈, 分类边界线为复杂的曲线. 从分类结果来看, 就第1组参数得到的分类结果更符合人们对分类期望.
为了能够训练获得最佳的分类超平面, 需要特征样本(即支持向量)具有一般代表性, 能够均匀分布于样本空间. 而事实上, 从上述三分类问题中可以看出,特征样本与核函数及其参数的选取密切相关. 不恰当的参数选择不可避免地会带来“欠学习”或“过学习”现象, 上述问题的分类结果就是典型的“过学习”现象. 通常选取合适的支持向量机参数需要依靠研究人员的实践经验或者不断尝试, 这大大影响了工作效率. 因此,采取启发式方法来优化支持向量机参数的方法能较好地解决了这个问题.
2.2 支持量机的目标选取
传统的支持向量机是基于等效间隔距离作为寻优目标的, 本质上是对泛化能力和经验误差的加权, 力示达到结构风险最低[14]. 然而, 该分类模型并没有考虑到数据样本不充分、样本分布不平衡的问题. 从前述三分类问题不难发现, 在少样本分类问题中, 当样本不能够均衡分布在样本空间中时, 特征样本应更具有一般代表性, 应越少越好, 如图1(a)所示.
在样本空间中, 支持向量决定着整个分类超平面,体现着整个样本集的分类特征. 支持向量的数量越多,分类边界越细致, 但“过学习”的概率也越大, 如图1(b)所示. 从分类的角度来看, 并不是支持向量越多, 分类器性能就越好, 而是支持向量在满足分类超平面的基础上,越少反而越好. 越少的支持向量说明越少的样本能够体现出分类特征, 对于最终的分类计算以及找出分类模式也是有好处的. 因此, 探寻最优分类超平面的过程不仅仅是要等效间隔距离大, 也要支持向量的数量尽量地少.
同时在训练集和测试集上的分类准确才是支持向量机的最终目标. 因此, 对样本的分类错误率也应作为模型的寻优目标[11].
综上所述, 在采用支持向量机进行分类时, 找到最优化超平面时的目标应该同时满足:
(1) 负等效间隔距离(记为tobj) 尽量地小. 在进行支持向量机求解时, 原本的求分类间隔最大问题, 已经被转换为求最小二次规划的问题.
(2) 支持向量的数量(记为tnsv)尽量地少. 用更少的支持向量来支撑分类超平面, 更不容易产生“过学习”现象, 同时被选中为支持向量的个体更能体现出故障的模式.
(3) 对样本的分类错误率(记为 terr)尽量地小, 也即要求支持向量机对样本识别更加准确.
这样, 在原先的单目标优化的支持向量机就被转换成了多目标支持向量机. 人们对分类问题的最终期望, 往往是在对这3个目标的协调权衡和折中处理后得到. 但首先需要使这些目标尽可能地达到最优, 由此可得到由若干个解组成的Pareto最优解集[15].
3 多目标支持向量机
多目标优化问题是指含有两个或两个以上的目标需要同时进行优化的问题[16]. 在多目标优化问题中, 约束条件会对目标产生严重的影响. 在求解多目标优化问题时,多个目标之间往往是相互排斥的. 不失一般性, 含n个决策变量, m个目标变量的多目标优化问题可以表述为:

其中, x =(x1,x2,···,xn)为 n维的决策向量, F (x)为m维的由目标函数构成的目标向量. 在多目标支持向量机问题中, 决策变量有3个, 分别为规则化参数C, 径向基函数系统方差δ和顺序最小化算法时梯度容忍系数ε, 即决策向量 x=(C,δ,ε). 目标变量也有3个, 分别为负等效间隔距离tobj, 支持向量数量tnsv, 以及错分率terr,即目标向量 F (x)=(tobj,tnsv,terr).
MOPSO算法的寻优过程与粒子群算法一样, 通过调整速度和粒子位置来实现全局寻优. 粒子的运动过程中同时向自身历史最优pi和全局最优g学习, 并不断更新速度以及位置:

采用精英保留策略, 需要构建两个种群, 分别是内部种群和外部种群, 其中内部种群是固定的, 而外部种群是变化的. 在迭代过程中, MOPSO从内部种群中选取一部分精英个体, 加入到外部种群中. 而在外部种群中, 又依据Pareto支配关系保证解的最优性. 当且仅当:
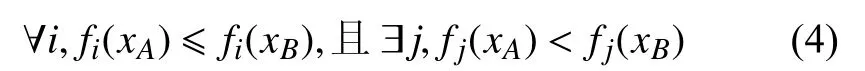
则称 xA支配 xB, 记为 xA≻ xB. 外部种群中的个体一旦被新的个体支配, 其将从种群中排除. 所以外部种群的个体就是当前时刻的非劣解, 或者叫Pareto最优解. 因此,当迭代到终止条件时, 只需要取出外部种群即可得到问题的最优解集.
如图2所示, 种群在开始进化时, 尽量地均匀分布在整个变量空间内, 以便更多地发现局部“深谷”, 这种能力即为算法的全局寻优能力. 但是当算法迭代到一定程度后, 内部种群会集中在某些局部区域进行局部寻优. 局部寻优不利于全局寻优, 因此需要在迭代一定次后重启内部种群部分个体, 这里设定为每隔50次迭代后重启10%的个体.
个体在寻优过程中需要向自身最优和全局最优学习, 学习因子的大小决定了学习速率的快慢, 也决定了算法进行全局寻优和局部寻优的能力差异. 这里采用动态学习因子策略, 即:
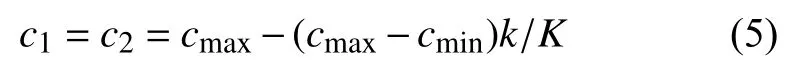
其中, k为当前迭代次数, K为最大迭代次数, cmax=2,cmin=1. 不难看出, 开始时学习因子较大, 加快算法收敛, 而到后面学习因子变小, 有利于算法拓展新的区域进行全局寻优.
同时, 为了保证解空间的均匀性和宽广性, 在保证新解不被支配的基础上, 设定外部种群的最大数量, 然后基于目标空间拥挤距离来淘汰外部种群中的个体.具体做法是当外部种群的个体数超过设定的最大数量时, 找出种群中密度距离最小的一个, 并将其排除, 从而维持均衡的外部种群. 基于以上分析, 得到算法1.

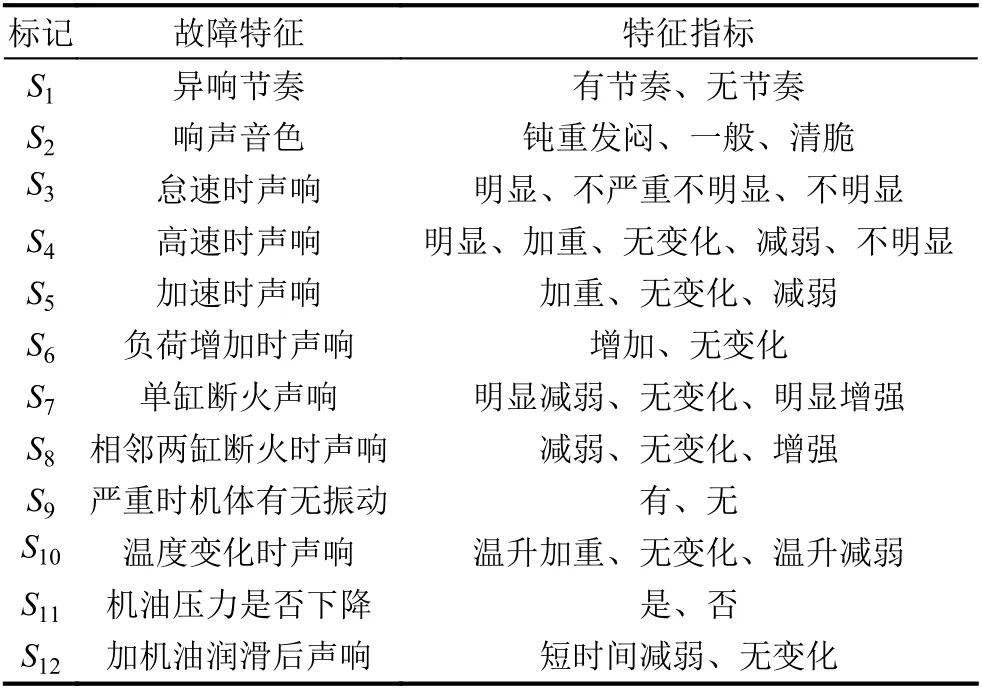
算法1. 基于粒子群的多目标支持向量机1 Initialize xi, vi of the population 2 calculate the objective value ti =( tobj, tnsv, terr)i of each particle xi 3 for i=1 to N do 4 for j=1 to Nnp do 5 if xi ≻xj (np) then remove xj (np) from the non-dominated population 6 if xj (np) ≻xi then break 7 if xi is not dominated then add to the non-dominated population 8 while iteration 28 if xi is not dominated then add to the non-dominated population 29 update the non-dominated population to keep it in a certain size 30 output the non-dominated population and their objective values 将算法1应用于前文所述的三分类问题中, 实验时采用径向基函数作为核函数, 内部种群大小设定为15, 外部种群大小为50. 为了更加直观, 达到更好的计算效率, 精简问题目标为F (x)=(tobj,tnsv). 最后得到Pareto前沿如图3所示. 可以看出, 在该问题中为了支撑三分类的分类线, 支持向量最少的数量为5个, 而最多的数量为41个, 当然也不排除一些被支配的解. 最大的目标值为-500, 最小的目标值为-2 836.27. 该问题最终得到的Pareto前沿较为平滑, 分布也较为均匀, 说明该非支配解集具有一定的代表性. 图3 三分类问题Pareto前沿 柴油机在正常工况下, 也会发出有节奏的声响, 但是其声响与产生故障时的声响不一样. 有经验的技术人员可以通过声响的节奏、音色、负荷、温度以及润滑等情况对发动机异响故障进行诊断. 因此, 在对其进行故障诊断时, 首先得确定其特征指标. 当柴油发动机发生异响时, 其产生异响可能来源于某个具体部位, 这些异响故障和正常声响构成了一个柴油机异响故障决策集合{曲轴主轴承响、连杆轴承响、活塞销响、活塞敲缸响、气门响、汽缸的漏气异响、正时齿轮响}, 将其标记为D={F1, F2, F3, F4,F5, F6, F7}. 如表1所示, 为了快速定位故障, 可以从异响节奏、响声音色、怠速时声响等12个方面进行诊断. 而这12个方面故障现象, 可以认为是柴油机不同异响来源的征兆, 从而构成了故障特征集合, 记为S, 其中每种故障特征又包含多个特征现象. 表1 故障特征指标 由于以上特征指标都是定性描述的, 因此需要对其采用模糊隶属关系进行量化, 将这种隶属关系离散化为μ={0.1, 0.3, 0.5, 0.7, 0.9}. 0.1表示不存在现象或减弱等, 0.9表示存在现象或增强, 而0.5表示介于两种现象之间或无现象变化等. 数值大小表示趋向于某一现象的严重程度. 当特征指标只包含2项时, 则从{0.1, 0.9}中选取隶属度值, 这些故障特征有{S1, S6, S9, S11, S12}; 当特征指标包含3项时, 则从{0.1, 0.5, 0.9}中选取隶属度值,这些故障特征有{S2, S5, S7, S8, S10}; 但是故障特征S3例外, 其从{0.1, 0.3, 0.9}中选取隶属度值; 而故障特征S4包含5项, 则需要从{0.1, 0.3, 0.5, 0.7, 0.9}选取隶属度值. 采用这种不是精确的0.1和0.9来表示0和1的方法可以更容易实现模糊关系的转换. 然而这些故障现象信息是通过历史经验总结得到, 大量信息是不确定的. 比如当正时齿轮故障产生异响时,异响可能有节奏, 也可能没有. 而且信息的收集也并不能保证所有信息都能够收集完备, 这种情况也可以当作不确定性信息, 在处理时采用模糊处理方式, 随机从给定序列中取值. 最后, 得到柴油发动机产生异响时故障特征隶属度矩阵(见表2). 其中, “—”表示信息不完备,即产生该故障时并不清楚是否产生对应的故障特征. 表2 故障特征隶属度矩阵 在获取的柴油机异响故障征兆信息表中包含不确定信息. 如果通过属性约简的方式, 可以提取一系列规则, 从而达到诊断故障的目的. 但是, 这就会导致一些非规则信息无法处理. 例如异响节奏属性, 通过约简后就会排除“无节奏”这一项, 因为其只在不确定性信息中存在, 而当异响产生且无节奏时, 现有的规则将无法判别. 因此, 需要采用蒙特卡罗模拟的方法可以得到一个确定的集合. 由于信息是离散化的, 在随机模拟时产生相同信息的可能性很大, 在状态识别前需要对这些信息进行整合得到有效集. 模拟仿真时以原样本集仿真100次,对重复信息整合, 最后再将得到的信息集随机分成两个集合, 分别进行训练和测试, 得到209个有效集, 其中125个用于训练, 84个用于测试. 在柴油机异响故障诊断问题中, 问题本身的不确定导致了部分训练样本并不可信, 或者说是实际不存在的, 但是又不清楚哪些信息不可信. 由于信息的不确定性, 虽然能过核函数的映射, 在高维空间中样本点之间不可分情况也大量存在. 因此, 需要对向量机的参数进行优化, 而且优化目标需要考虑分类器的错分率. 综上所述, 该多目标支持向量包含以下3个目标: 负等效间隔距离tobj, 支持向量数量tnsv, 错分率terr. 需要说明的是, 在广义线性可分的情况下, terr与 tobj是一致的. 采用多目标支持向量机对该问题求解. 求解时采用径向基函数作为核函数, 内部种群大小设定为15, 外部种群大小为50, 自身历史最优数量最大为5, 采用定期重启和动态学习因子. 最后得到非劣解集如表3所示, 共包含46个非劣解. 根据支持向量机的原理, 在广义线性可分的情况下, terr与 tobj是一致的. 但是从表3中的结果来看, 负等效间隔距离tobj最小的为序号1的解, 值为-3 890, 而它对应的错分率terr为 19.2%, terr的 值并没有随着tobj减小而减小, 说明该问题实现不了广义线性完全可分. 而且,解1的支持向量达到24个, 是解46 (tnsv=11)的2倍多, 说明其已经出现了“过学习”问题, 很明显不是最优解. 如果不进行参数优化, 用支持向量机对该问题进行求解, 得到结果可能是表3中的任一个解, 显然不是最优的. 如果以tobj、 terr或 tnsv中 的某一个作为目标进行优化, 得到的也并不一定是最优的. 表3 非劣解集的目标值 采用多目标支持向量机, 既可以排除人为设定参数时需要依靠经验的风险, 也可以排除单一目标产生“过学习”的风险. 多目标支持向量机基于目标互不支配的思想产生一系列解, 至于哪个解是需要的, 可以根据人的偏好来确定. 模糊综合评判法[17]具有结果清晰, 系统性强的特点, 能较好地解决模糊的、难以量化的问题, 适合于上述这种非确定性问题的评判. 最后, 采用模糊综合评判法从结果集中筛选出期望的综合最优解. 在该问题中, 由于测试集的存在, 所以在最佳的评判时需要考虑测试的情况, 而且还应考虑“过学习”的情况. 因此评价指标要比原问题要多, 可以定为以下指标: 负等效分类间隔u1、训练样本错分率u2、训练集分类间隔u3、测试样本错分率u4、测试集分类间隔u5、“过学习”情况u6等. 从而得到因素集U={u1,u2,u3,u4,u5,u6}. 其中分类间隔u1采用式(6)计算: u5参照式(6)计算, 而“过学习”情况u6可以通过训练集和测试集的错分情况对比得到: 因素集与评判集之间的关系可以通过隶属度函数[17]计算. 因素{u2, u5} 采用正相关的隶属函数, 因素{u1, u3, u4, u6}采用负相关的隶属函数. 计算各因素的隶属度值, 得到模糊关系矩阵 R =(rij)6×46. 再采用加权平均模型M(·, ⊕)评价最优解. 加权的时候突出错分率指标, 确定权重系数为: 再根据式(8)计算得到综合评判指标如表4所示. 表4 综合评判指标 根据上述综合评判指标, 第43个解为综合最优解(如图4所示), 其对应的支持向量机参数(C, δ, ε)为(792.5, 10.43, 0.571 3), 其对应的3个目标值分别为: 负等效间隔距离 tobj=-1304, 支持向量数量tnsv=16, 训练集错分率terr=0.032. 该分类器对测试集的错分率也只有0.0357. 综合对比发现, 该解的错分率以及等效分类间隔在训练集和测试集上都是最好的. 说明采用该组参数的支持向量机不仅具有较高的正确识别率, 而且结构风险最低, 达到了最佳的分类期望. 图4 柴油机异响故障问题非劣解集及综合最优解 在综合评判指标中, 次综合最优解为第42个解,当u1得到的权重调整为0.2时, 该解将成为综合最优解. 因此, 当人们的期望不同时, 可以适当调整评判权重, 即可筛选出期望的综合最优解. 图5所示为分类器的迭代性能曲线. 从图中的在线性能曲线可以看出, 算法开始迭代后能快速收敛, 并很快脱离局部最优点展开全局寻优. 从离线性能曲线可以看出, 算法大约在迭代至150次后找到全局最优,并不再收敛. 综合来看, 算法针对此类问题收敛速度较快, 且有效避免了局部陷阱, 工作效率高. 图5 分类器迭代性能曲线 支持向量机作为当前最好的分类工具之一, 在少样本、非线性问题上表现出了许多优势, 在故障诊断、模式识别等多个领域具有广泛的应用. 然而, 不恰当的参数选择就如同给机器下错了“指令”, 往往得不到最好的结果. 启发式优化算法的引入, 可以快速找到支持向量机的最佳参数. 但是单纯以等效间隔距离为目标的寻优方法,但是也可能导致结构风险增加, 从而发生“欠学习”或“过学习”现象. 使用多目标粒子群算法对其优化, 能得到一系列均衡分布的非支配解集, 扩大了目标范围, 从而降低了结构风险. 柴油机异响故障诊断问题表明, 该方法能够快速收敛, 并得到一系列非劣解, 有效解决少样本、不完备或不确定故障征兆问题, 通过综合评判方法筛选得到的综合最优解更符合人们的期望.

4 柴油机异响故障诊断
4.1 特征指标的确定

4.2 故障状态识别

4.3 综合最优解筛选



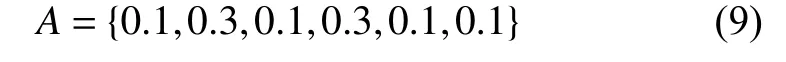



5 结论与展望
