基于回流能量调节的液压执行机构运动位移控制仿真研究

2022-09-20吕文龙张广毅

机床与液压 2022年9期

吕文龙，张广毅

(1.新乡职业技术学院数控技术系，河南新乡 453000； 2.郑州大学机械与动力工程学院，河南郑州 450001)

0 前言

随着中国制造业的迅猛发展，液压技术也得到了很大的改进。液压技术具有传动稳定、抗负载能力强及响应速度快等优点，目前广泛应用于工业机器人、挖掘机、汽车及导弹发射等领域。液压系统通常由5个部分构成：动力元件(液压泵)；执行元件(液压马达、液压缸等)；控制元件(液压阀)；辅助元件(油箱、管路蓄能器等)；工作介质(液压油)。液压缸通常用作驱动系统中的执行机构，在驱动过程中能够获得较大的力。液压执行机构数学模型相对复杂，存在控制方向未知、比例阀零点不准确等问题，传统控制方法很难得到令人满意的控制效果。因此，研究更好的控制系统，对于液压技术的发展至关重要。

目前，为改善液压执行机构控制系统输出效果，国内外科研工作者对液压执行机构控制系统进行了许多理论研究。文献[3-4]研究了液压执行机构模糊PID控制方法，介绍了变排量液压马达系统原理，设计了模糊PID控制器，通过模糊规则对PID参数进行调节，搭建液压系统仿真模型，液压系统在响应速度和稳定性方面得到了改善。文献[5-6]研究了液压执行机构神经网络滑模控制系统，建立液压驱动平面简图模型，推导出液压缸位置运动方程，利用神经网络算法对滑模控制器进行逼近，采用MATLAB软件对液压缸活塞运动轨迹进行仿真，提高了液压执行机构运动轨迹的控制精度。文献[7-8]研究了电液伺服液压执行机构位置的滑模控制方法，建立了液压执行机构简图，分析了液压执行机构工作原理，对液压执行机构进行数学建模，推导出液压缸流量方程，设计滑模变结构控制器，通过仿真检验了执行机构的位置跟踪效果，液压执行机构运动位置精度得到了提高。以上研究的液压执行机构控制精度虽然有所提高，但是在突变位移信号或者重载状态下，其运动位移跟踪误差较大。对此，本文作者建立回流能量调节的液压系统模型装置简图，推导液压流量和动力学方程。引用滑模控制器并进行改进，设计超螺旋滑模控制的液压系统。为从理论上验证液压控制系统的稳定性，采用李雅普诺夫函数对超螺旋滑模控制器进行验证，通过MATLAB软件对液压执行机构运动位移跟踪信号进行仿真，并与传统滑模控制器的输出效果进行对比，为进一步研究液压执行机构运动位移控制系统提供参考。

1 系统数学模型

液压系统模型如图1所示。液压泵工作时，将油箱里面的油吸入到液压缸无杆腔，通过差动阀将有杆腔中的油返回到无杆腔中，从而推动活塞杆快速前进。当压力过高时，通过安全阀将油返回到油箱中。

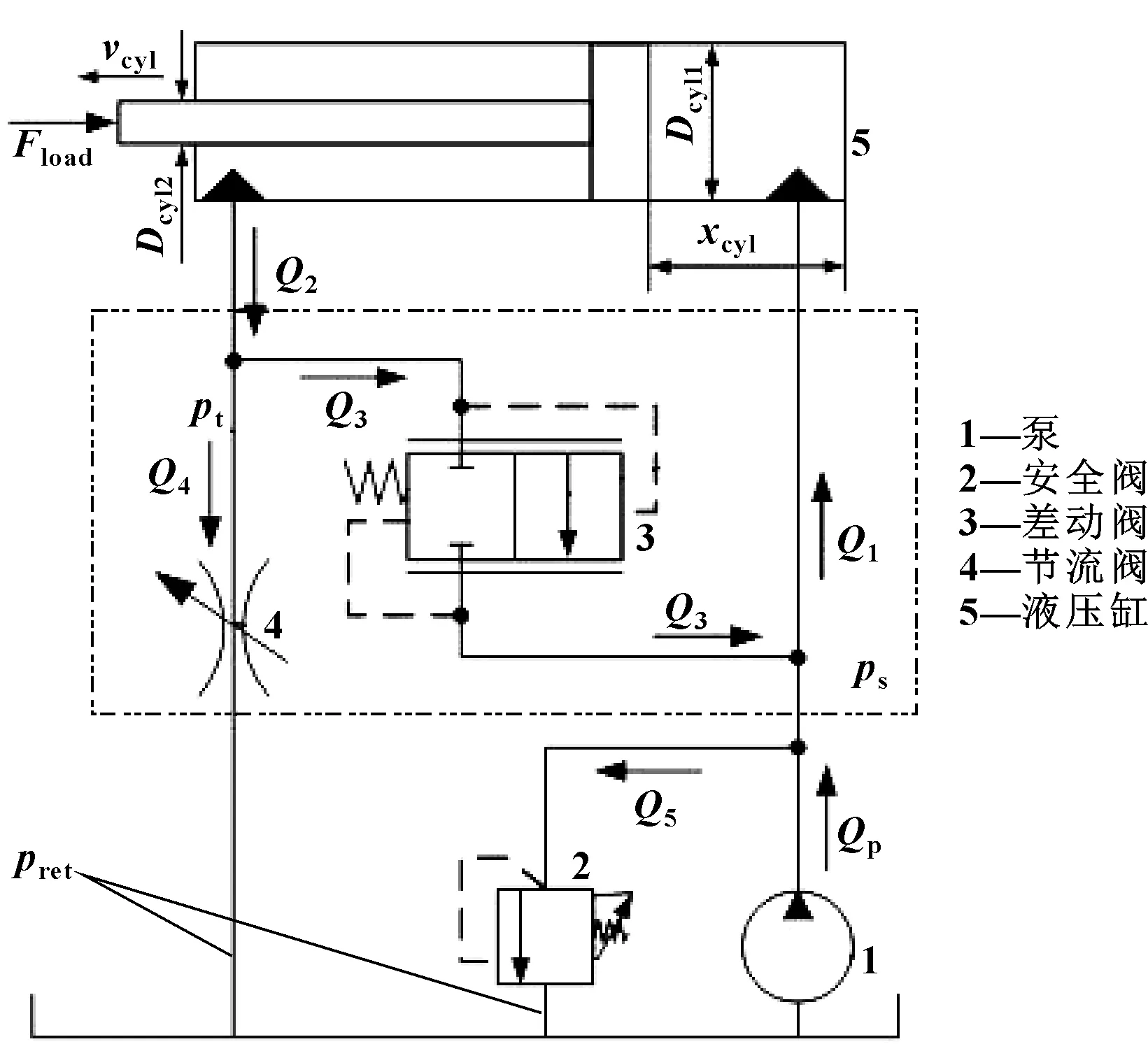
图1 液压系统模型

如果没有通过差动阀的流量，液压执行机构理论速度计算公式为

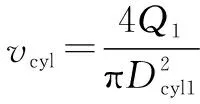
(1)

式中：=-，为进入无杆腔油的流量,为泵的流量,为安全阀的流量;为液压缸直径。

在一个带有差动阀的系统中，执行机构的回流被引导回供给管路，使用相同的定速泵可以显著改变活塞杆的速度，获得的连杆速度可能低于、等于或高于返回运动速度，但是活塞速度的计算复杂得多，因为=-+，其中：差动阀的流量取决于有效负载和节流阀设置，则泵产生的流量数学模型可以定义为

(2)

式中：为启动时间。

供给管路的压力随时间变化的计算公式为

(3)

式中：为流体体积模量；为活塞运动位移；为活塞无杆腔截面积；为供给管路体积。

同样，节流阀压力随时间变化的计算公式为

(4)

式中：为液压缸有杆腔的流出流量；为差动阀的流量；为通过节流阀的流量；为活塞杆的截面积；为负载管路体积。

活塞杆运动速度和加速度分别定义为

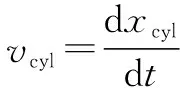
(5)

(6)

式中：为供给管路压力；为负载管路压力；为负载；为阻尼系数；为活塞质量。

根据活塞杆运动速度，得到和分别为

(7)

=(-)

(8)

差动阀升程运动方程为

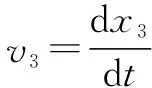
(9)

(10)

式中：为差动阀的直径；为差动阀的速度；为阻尼系数；为刚度系数；为摩擦因数；为差动阀的质量。

根据伯努利方程，差动阀流量方程为

(11)

=π

(12)

式中：为差动阀的间隙；为差动阀流量系数；为流体密度。

节流阀流量的计算方法与类似，只是在这种情况下，节流间隙有一个固定区域，具体取决于。操作员可使用阀门旋钮调整间隙区域。当回流管压力低于负载管压力时，计算公式为

(13)

式中：为回油管压力；为节流阀流量系数；为节流阀的间隙。

通过安全阀的流量的运动方程具有以下形式：

(14)

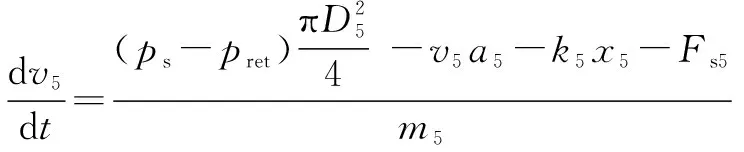
(15)

初始弹簧张力，在供应管路中的压力超过20 MPa时提供阀门开启所需的力。在这种情况下，形成直径为、宽度为的圆柱形间隙。因此，流量计算公式为

(16)

其中：

=π

(17)

2 控制系统

2.1 超螺旋滑模控制

超螺旋滑模控制是对传统滑模控制的改进，是一种高阶滑模控制方法，能够使滑动变量和对应的导数趋向于零，有效降低滑模控制器的抖动幅度。

液压系统状态变量设置为

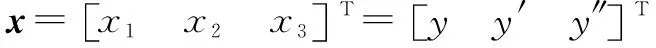
(18)

液压系统执行机构位置表达式定义为

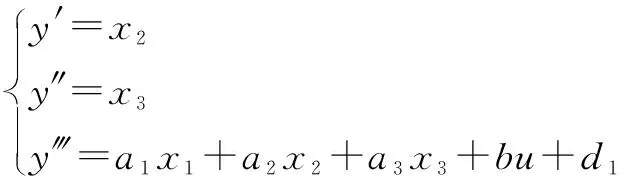
(19)

式中：、、为未知参数；为流量控制方向；=Δ+,Δ为零点偏离信号,为外部干扰；为控制信号。

假设1：输入信号的导数为连续有界。

控制系统误差变量设置为

(20)

滑模面定义为

=++

(21)

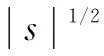
对滑模面进行求导后得到：

′=++++++-‴

(22)

超螺旋滑模控制器设计为

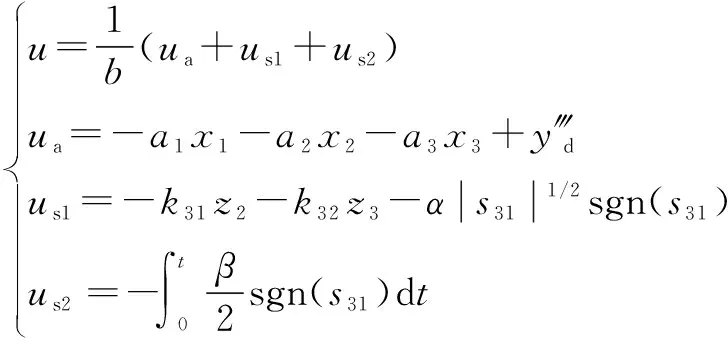
(23)

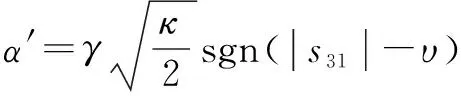
(24)

式中：、为控制器时变增益;、、、为任意正数。

采用超螺旋滑模控制的液压执行机构控制流程如图2所示。

图2 液压执行机构位移控制

2.2 控制系统稳定性分析

根据李雅普诺夫函数可得：

(25)

对公式(25)求导可得：

′=(++++++

-‴)

(26)

将式(23)(24)代入式(26)得：

′=

(27)

(28)

则′可以表示为

′=[-||12sgn()-sgn()]

(29)

若>0，则式(29)变为

′=-||32-(-)||

(30)

即只要>，就可以得到′<0。

若<0，则式(29)变为

′=-||32-(+)||

(31)

即只要>-，就可以得到′<0。

由以上分析可知，选取合适的参数，满足以上条件时就可以得到′<0。根据李雅普诺夫稳定性判别定理，可得超螺旋滑模控制系统是稳定的。

3 结果与分析

通过仿真实验验证滑模控制器和超螺旋滑模控制器的控制效果，采用MATLAB软件对液压执行机构运动位置跟踪误差进行仿真，并对仿真结果进行对比和分析。仿真初始参数如表1所示。

表1 仿真参数

假设执行机构运动位移为正弦波信号和阶跃波信号，在无负载状态下，液压执行机构正弦波、阶跃波信号跟踪结果分别如图3、图4所示。在有负载状态下，液压执行机构正弦波、阶跃波信号跟踪结果分别如图5、图6所示。

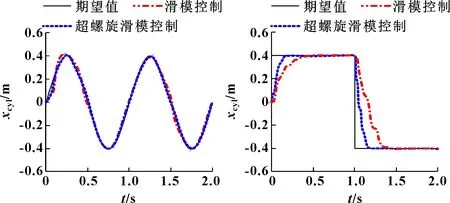
图3 正弦波信号跟踪(Fload=0) 图4 阶跃波信号跟踪(Fload=0)

图5 正弦波信号跟踪(Fload=20kN) 图6 阶跃波信号跟踪(Fload=20 kN)

由图3可知：跟踪信号为正弦波信号时，在空载情况下，采用滑模控制器时，液压执行机构位移跟踪在025后才达到稳定状态；采用超螺旋滑模控制器时，液压执行机构位移跟踪在009后就达到了稳定状态，自适应调节时间缩短了64。两种控制器在稳定前都有偏离，差别不大，但是稳定后运动位移与期望值偏差都较小。由图4可知：跟踪信号为阶跃波时，在空载情况下，采用滑模控制器时，液压执行机构位移跟踪在041后才达到稳定状态；采用超螺旋滑模控制器时，在017后就达到了稳定状态，自适应调节时间缩短了585，超调量都为0，稳定后运动位移与期望值偏差较小。由图5可知：跟踪信号为正弦波时，在负载为20的情况下，采用滑模控制器时，液压执行机构位移跟踪在033后才达到稳定状态，稳定后运动位移与期望值偏差较大；采用超螺旋滑模控制器时，在009后就达到了稳定状态，自适应调节时间缩短了723，稳定后运动位移与期望值偏差较小。由图6可知：跟踪信号为阶跃波时，在负载为20的情况下，采用滑模控制器时，液压执行机构位移跟踪在05后才达到稳定状态，超调量为375；采用超螺旋滑模控制器时，液压执行机构位移跟踪在017后就达到了稳定状态，超调量为0，自适应调节时间缩短了66，稳定后运动位移与期望值偏差较小。因此，在同等条件下，采用超螺旋滑模控制的液压执行机构时，执行机构运动位移跟踪精度较好，自适应调整时间较短，控制效果较好。