基于模糊自整定方法的液压马达驱动工作轴速度控制的研究
2022-09-20王瑞玲张强
王瑞玲, 张强
(1.吉林铁道职业技术学院机械工程学院, 吉林吉林 132000; 2.大连工业大学机械工程学院,辽宁大连 116034)
0 前言
液压系统自动传动与控制是机械加工与装备行业的高新技术发展方向之一。由于其结构紧凑、扭矩传递大、响应速度快、自润滑、液体传热性能好、系统寿命长等突出特点,被广泛用于工业制造。液压系统的自动传动与控制系统通过液压马达控制工作轴的转动速度,进而实现对生产过程的控制。
为实现对液压马达驱动工作轴速度的控制,研究人员提出了多种控制方法。EGOROVA等建立了液压传动控制系统的数学模型,提出一种基于横向速度反馈回路控制的液压传动自动控制机构的运行算法,用以控制液压马达的转速。曹付义等针对液压马达传动系统在变速输入时输出转速低、控制困难的问题,以PID方法为基础,设计了双前馈模糊PID速度控制方法,以控制液压马达的速度。CAO研究了电液伺服系统的工作原理、系统模型和系统控制理论,提出了遗传算法优化的PID控制器,以实现对液压马达的控制。以上方法可以控制液压马达的速度,但控制准确度有待提高。
对此,本文作者在研究液压马达驱动工作轴速度控制系统的结构和数学模型的基础上,以神经网络控制为依据,结合模糊控制理论,设计模糊自整定液压马达速度控制方法。通过最速下降法求取隶属函数层的中心值和宽度,以及输出层的加权系数。设计计算隶属函数层的节点输出信号的模糊规则,从而实现对液压马达的自整定控制。通过速度控制实验,验证所提方法的有效性。
1 速度控制系统的结构分析
液压马达驱动的工作轴速度控制系统由安全阀、V形皮带、液压马达以及比例阀等部分组成,如图1所示。

图1 液压马达驱动的工作轴速度控制系统结构
在图1中,M为三相电动机,为系统的控制输入信号。三相电动机通过V形皮带驱动油泵齿轮动作。油泵的工作压力通过一个安全阀控制。液压马达的速度由比例阀控制的液压流量进行调节。在泵到比例阀的油管路上,有一个高压过滤器和蓄电池构成的补油装置,用于积累和补偿油势能。
另外,液压马达通过V形皮带将旋转传递给工作轴,工作轴上的速度表作为速度传感器来测量速度。速度表通过传动带接收工作轴的速度信号。在图1所示的系统结构中,用油泵作为负载设备,便于通过溢流阀和安全阀改变油泵的供给压力,以改变负载的状态。
2 速度控制系统的数学建模
在速度控制系统中,考虑液压马达转子上的摩擦力和惯性矩,速度控制系统中液压系统的自动传动与控制过程如图2所示。
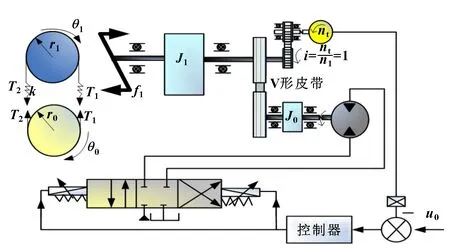
图2 液压系统的自动传动与控制过程示意
在图2中,和分别为动滑轮半径和从动滑轮半径,和为滑轮不同侧的皮带拉力,和分别为转子转角和工作轴转角,和分别为电机惯性和负载惯性,为工作轴转速,为输入速度传感器的转速,为工作轴摩擦因数。
工作轴上的力矩方程为
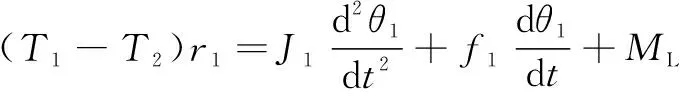
(1)
式中:为工作轴上的载荷。
和的计算公式为
=(-)
(2)
=(-)
(3)
式中:为V形皮带的刚度。
速度传感器的反馈值的计算公式为
==
(4)
式中:为速度传感器的增益。
在液压马达上,可通过、以及来求取液压马达转子的力矩方程:

(5)
式中:为马达转子的位移;为供给压力;为电机等效黏滞系数。
通过可求取液压马达的流量方程:

(6)
式中:为流经液压马达的流量;为电动机泄漏系数;为油液单位体积弹性模量,计算公式如下:
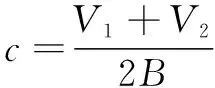
(7)
式中:+为管道内油液的总体积;为油液的体积模量。
在忽略阀门的流量损失时,可通过比例阀的阀门流量增益来求取:
=
(8)
式中:为流经比例阀的电流。
综合式(1)—式(5),可得到:

(9)
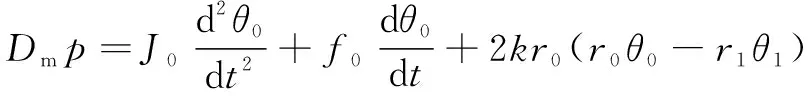
(10)
工作轴转速为
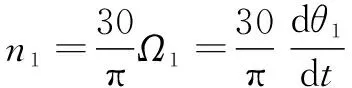
(11)
通过速度传感器的反馈值,可求取控制器的输入量:
=-
(12)
联合式(4)—式(12),可得速度控制系统的状态方程为
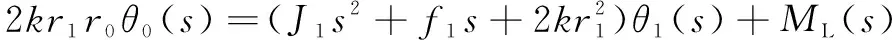
(13)
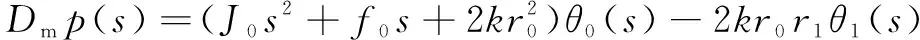
(14)
()=()+(+)()
(15)
()=()
(16)
=()
(17)
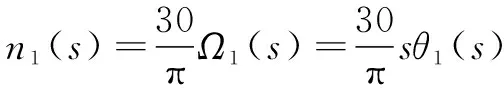
(18)
()=()-()
(19)
式中:为频域参数。
3 模糊自整定控制器的设计
通过图2可知,液压系统的自动传动与控制过程为一个闭环过程,且从速度控制系统的状态方程可知速度控制过程为一个非线性的动态过程。因此,为克服控制过程的非线性,以及适应闭环系统的控制要求,在神经网络的基础上,设计模糊自整定方法,用于控制液压马达驱动工作轴的速度。
神经网络可适用于通过多个输入变量求取一个输出的控制场景。神经网络的结构如图3所示。
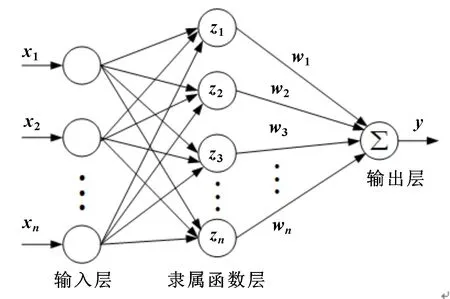
图3 神经网络结构
从图3可见,神经网络分为3层,在输入层中,将外部输入信号传入神经网络中。将目标速度值与实际速度值的差,及的变化率Δ作为输入信号。
=-
(20)
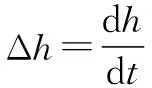
(21)
获得输入信号后,隶属函数层将利用输入信号,通过隶属函数,求取该层的节点输出信号:
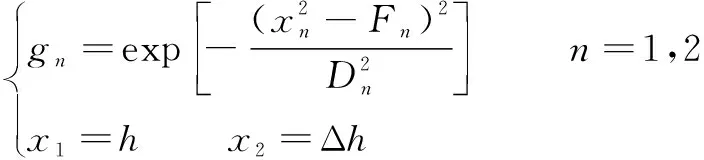
(22)
式中:和分别为的中心值和宽度。
将进行加权,以求取输出层的输出值:
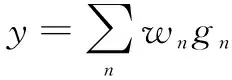
(23)
式中:为加权系数。
在最速下降法的基础上,通过学习步长计算+1时刻、以及的值:
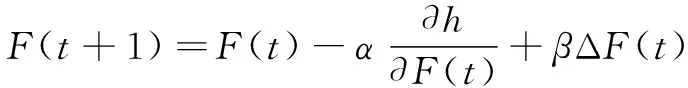
(24)
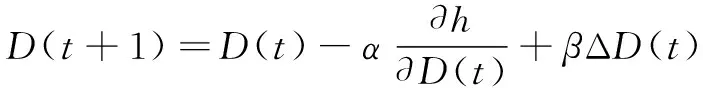
(25)

(26)
式中:为平滑因子。
将Δ和的模糊子集用NB(负大)、N(负)、Z(零)、P(正)和PB(正大)表示,和的模糊子集用S(小)、MS(中小)、M(中)、MB(中大)和B(大)表示,则设计如表1、表2所示的和的模糊规则,以求取和。

表1 g1的模糊规则
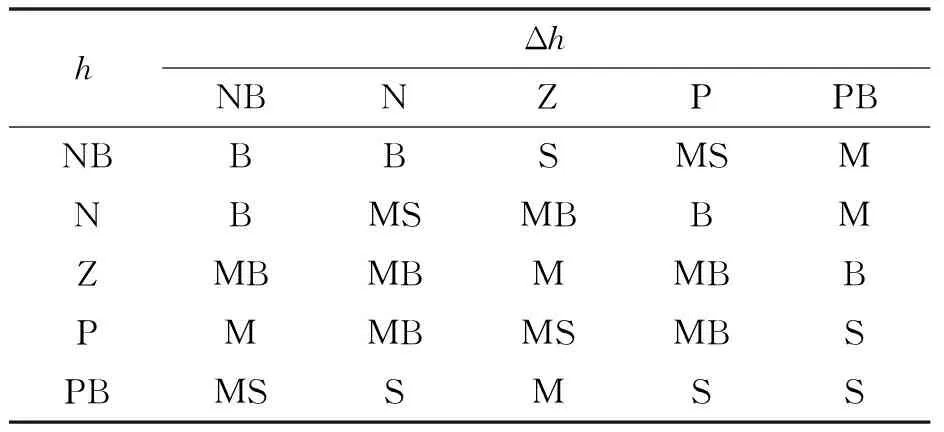
表2 g2的模糊规则
由此可见,通过设计的模糊规则,在不同时刻的速度误差及其变化率的基础上,可自整定地获取和的值,从而实现对速度的控制。
4 实验结果
利用Intel I5 CPU、8 GB内存的PC作为硬件平台,采用MATLAB/Simulink软件作为软件平台,按照表3所示的主要参数,建立仿真模型,用于对所提模糊自整定(Fuzzy Self Tuning,FST)方法的速度控制有效性验证。实验中,引入PID方法用于实验对比,便于更好地观察FST方法的控制结果。
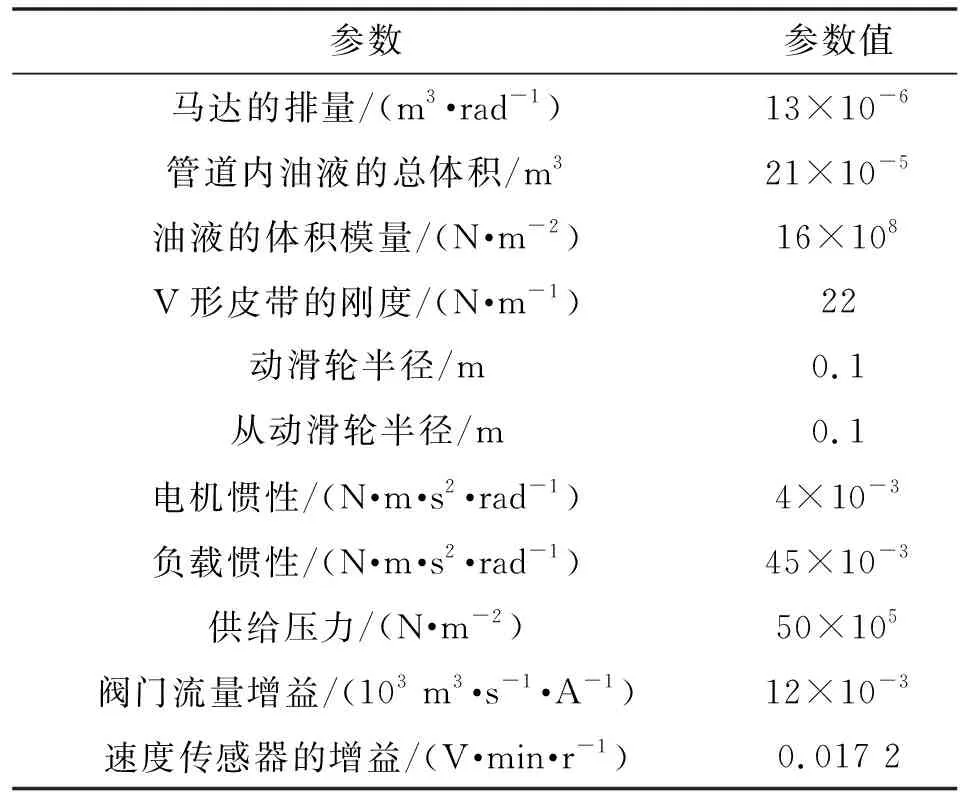
表3 主要参数
4.1 响应灵敏度测试
设定200、400、600 r/min 3个目标速度。利用FST方法和PID方法对所设的3个目标速度进行追踪。通过分析FST方法和PID方法的追踪结果,以分析各方法的响应灵敏度。图4所示为利用FST方法和PID方法追踪3个目标速度的结果。
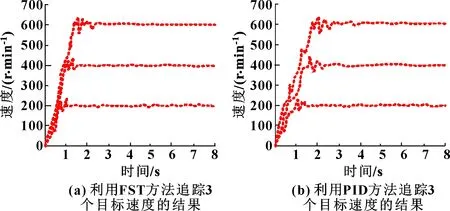
图4 FST方法和PID方法的响应灵敏度测试结果
由图4可见,利用FST方法追踪3个目标速度时,分别在为0.82、1.02、1.48 s时就到达了200、400、600 r/min这3个目标速度,经过短暂调整后,分别于1.03、1.61、2.32 s处于稳定状态。而利用PID方法追踪3个目标速度时,分别在为0.98、1.79、1.92 s时才到达了200、400、600 r/min这3个目标速度,经过调整后,分别于1.48、2.38、2.86 s处于稳定状态。由此可见,FST方法具有更高的响应灵敏度,能够较快地响应速度的变化要求。
4.2 随机变化速度追踪测试
为测试FST方法和PID方法对速度的追踪准确性,采用FST方法和PID方法对随机变化的速度进行追踪,速度追踪结果如图5所示。
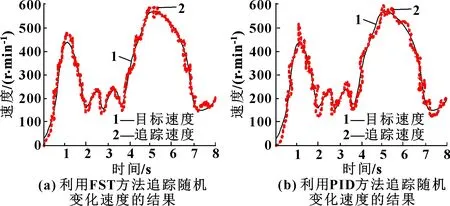
图5 FST方法和PID方法对随机变化速度的追踪结果
由图5(a)可见:FST方法在追踪随机变化速度时,在1.1 s附近出现了追踪过程中较目标速度的最大偏差,此时偏差为9.09%;经过调整,在1.3 s附近,FST方法追踪速度又趋于目标速度,并在后续对目标速度的追踪过程中,仅出现了一次较大的偏差。从图5(b)可见:PID方法在追踪随机变化速度时,在1 s附近出现了追踪过程中较目标速度的最大偏差,此时偏差为18.21%;经过调整后,在1.5 s附近,PID方法追踪速度又趋于目标速度,但在后续对目标速度的追踪过程中,出现了3次较大的偏差。由此可见,FST方法对随机变化的速度具有较好的追踪性能。
为进一步观察FST方法和PID方法的控制性能,将这2种方法在追踪随机变化速度时的输入信号进行对比。图6所示为FST方法和PID方法在追踪随机变化速度时的输入信号变化情况。
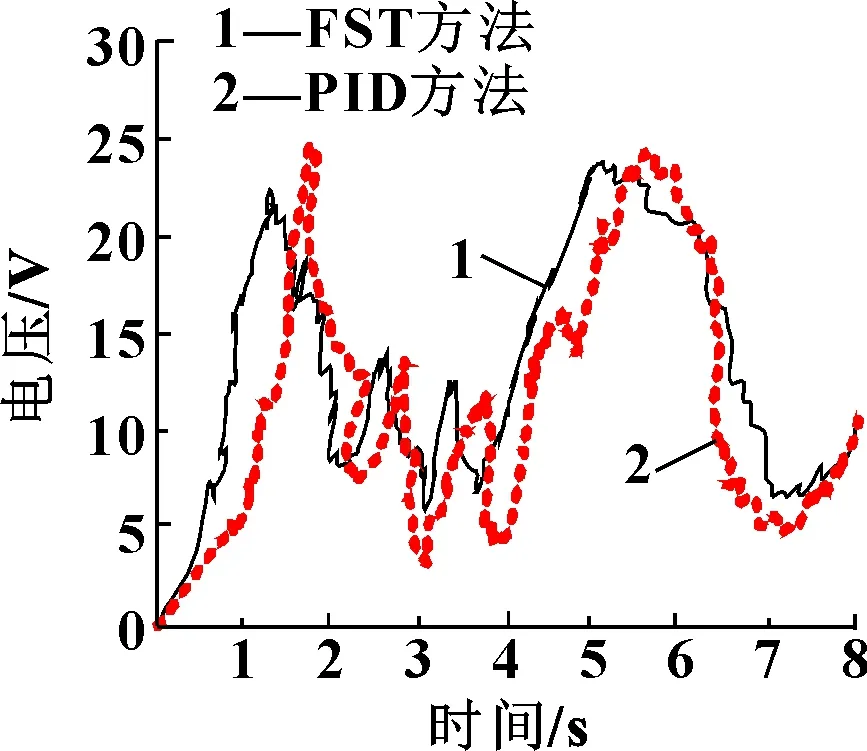
图6 FST方法和PID方法在追踪随机变化速度时的输入信号变化情况
由图6可见:FST方法的输入信号能够根据目标速度的变化作出快速的响应,而且整个追踪过程振荡次数较少;而PID方法的输入信号变化较为迟钝,不能较好地根据目标速度的变化作出快速的响应,而且整个追踪过程振荡次数较多。由此可见,FST方法不仅能够对目标速度进行准确的追踪,而且在目标速度发生变化时,响应速度也较快。
5 结语
本文作者分析了液压马达驱动的工作轴速度控制系统的结构,又对该速度控制系统进行了数学建模,求取了它对应的状态方程,明确了速度控制的过程为一个闭环的非线性过程。以神经网络为基础,采用最速下降法计算了神经网络中隶属函数层的中心值和宽度,以及输出层的加权系数,并设计了模糊自整定方法,求取了隶属函数层的节点输出信号,从而实现了对速度的控制。结果表明:所提方法在追踪目标速度时,响应灵敏度较高,追踪结果较为准确,验证了所提方法对液压马达驱动工作轴的速度控制具有较好的有效性,可以提高速度控制的准确性。
