基于非线性磨削模型的稳态与颤振抑制的研究

杨铎，陈添定，李鹤，饶成飞

(1.大连大学机械工程学院，辽宁大连 116622；2.东北大学机械工程与自动化学院，辽宁沈阳 110819)

0 前言

在机械加工过程中，工件的加工质量与切削过程的稳定性有关。当过程参数选择不当时，会发生切削颤振，导致加工的零件质量不满足工艺要求。针对这一问题，许多学者进行了研究。

为抑制颤振，提高加工质量，许多学者也进行了相关研究。KONG等通过对主轴转速进行混沌摄动，成功抑制了车削过程中的颤振。MORADIAN等采用自适应滑模控制抑制镗削过程中的再生颤振。LI等采用变刚度的方法抑制深孔镗削过程中的颤振。吴胜利等采用双时间延迟动力学模型，通过周期性改变砂轮和轧辊的转速，抑制了轧辊磨削过程中的颤振。

以上研究中大多考虑的线性模型和切削力非线性模型，而在轧辊磨削中，砂轮相较于轧辊为弱刚度结构。因此，本文作者引入Duffing振子作为砂轮结构非线性，建立三自由度磨削系统非线性动力学模型，研究稳态叶图边界曲线附近参数变化对磨削过程稳定性的影响。为抑制边界曲线附近的颤振，采用混沌摄动方法抑制颤振。

1 磨削系统动力学模型

磨削系统通常由床身、头架、尾架、磨头、纵横托板等部件组成。砂轮在水平和竖直方向产生运动，而工件只在水平方向拥有一个自由度，系统的动力学模型简图如图1所示。图中:、、分别为砂轮的质量、阻尼、刚度；、、分别为工件的质量、阻尼、刚度；、分别为砂轮和工件的转速；、分别为砂轮和工件的位移。

图1 磨削系统动力学模型

根据磨削系统动力学模型，建立磨削系统动力学方程：

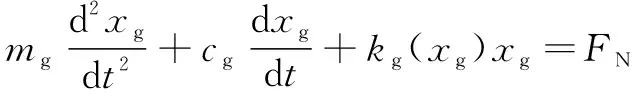
(1)

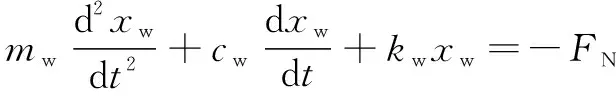
(2)

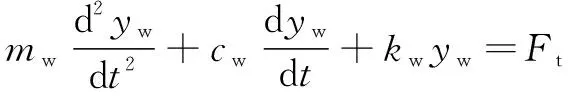
(3)

由于砂轮在竖直方向的运动，在磨削过程中，砂轮与工件表面会产生一个夹角，如图2所示，但可以看出砂轮在竖直方向的位移远小于工件半径与砂轮半径之和，因此假设文中的角度为0。

图2 砂轮竖直方向运动示意

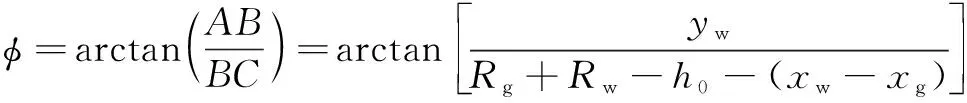
(4)

()=+()-(-)-()+

(-)

(5)

式中：为砂轮与工件的磨削重叠率；和分别为磨削过程中砂轮和工件的旋转周期，表达式为

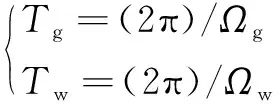
(6)

砂轮与工件之间的法向磨削力为，为砂轮与工件之间的磨削系数，为有效磨削宽度。当磨削深度为0时，即砂轮表面离开工件表面，法向磨削力变成0，则：

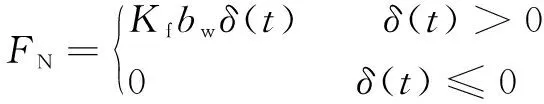
(7)

为砂轮与工件之间的切向磨削力:

=sign()

(8)

由于砂轮在竖直方向的运动，砂轮表面与工件表面在接触点的相对磨削速度为:

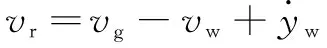
(9)

将公式(5)—(8)代入公式(1)(2)(3)，整理可得

(10)

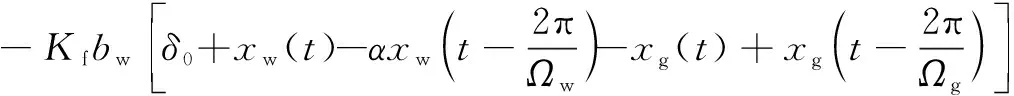
(11)

(12)

2 磨削过程稳态与分岔分析

根据实际工况选定轧辊磨削系统主要参数如表1所示。

表1 磨削系统参数

采用MATLAB中的数值分析工具箱DDEBIF-TOOL对轧辊磨削系统延迟微分方程进行求解。当磨削重叠率=1时，得到系统的稳态叶图如图3所示。可以看出，稳态边界曲线将参数平面划分成两部分，稳态边界以上为不稳定磨削区域，稳态边界以下为稳定磨削区域，其中稳态边界与极限磨削宽度之间的区域称为条件稳定区域，而极限磨削宽度之下的区域称为无条件稳定区域。

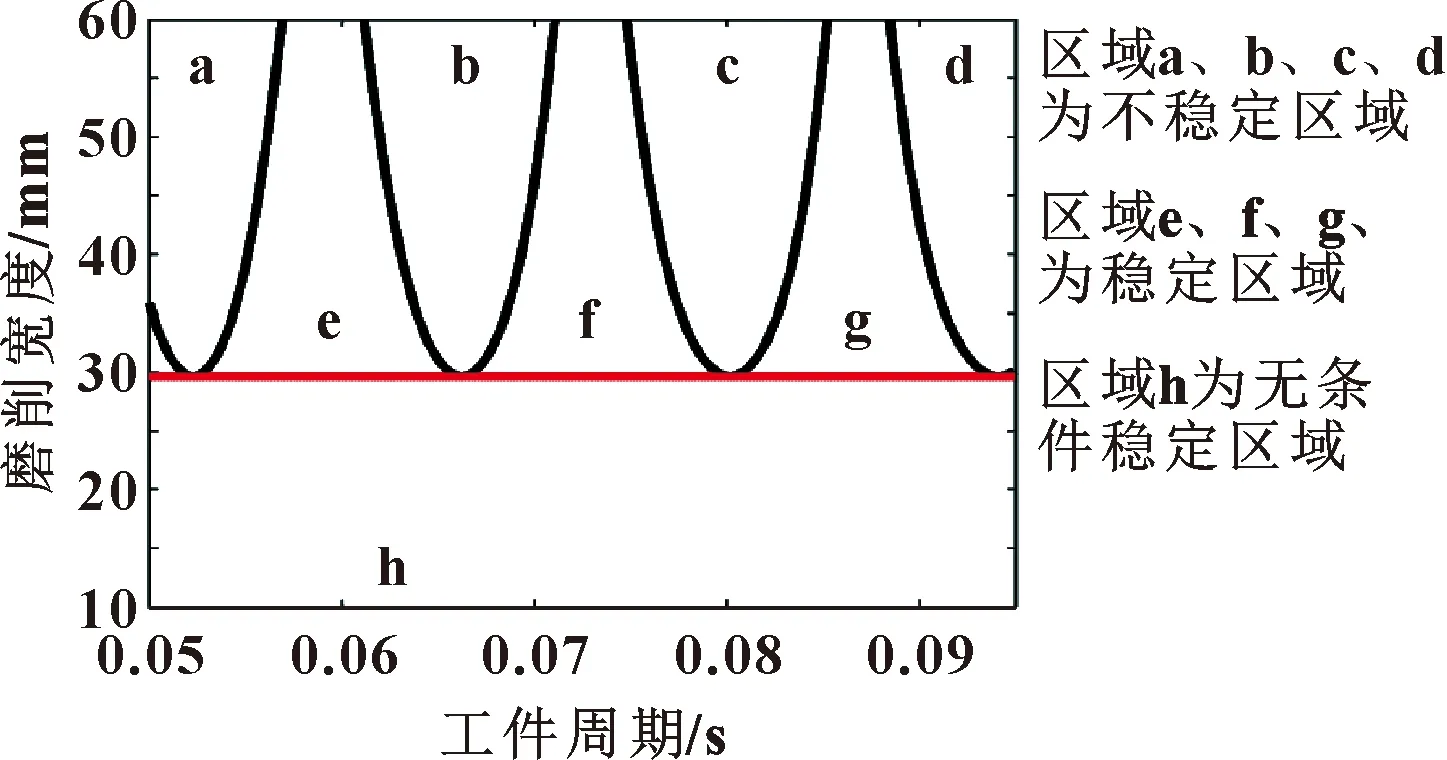
图3 稳态图

根据图3，当减少磨削宽度到无条件稳态区域时，可以提高磨削过程的稳定性，从而提高磨削工件的质量。但是，当磨削宽度较大时，要选择合适的工件转速才能使得磨削过程保持稳定，即过程参数要位于条件稳定区域。而在实际的轧辊磨削加工过程中，为提高加工过程的稳定性，通常参数值都选在远离稳态边界区域，甚至选在无条件稳态区域，这不仅限制了轧辊磨削效率，而且增加了企业的成本。因此，本文作者对稳态边界附近过程参数变化对磨削过程稳定性的影响进行研究。

选择特定的工件旋转周期区间，画出磨削系统关于工件旋转周期的分岔图，如图4所示。可以看出：系统关于工件旋转周期发生亚临界分岔，当工件旋转周期从较小值逐渐增大到较大值时，系统幅值首先保持不变，然后突然跳跃到一个较大的值，此时系统产生一个极限环；而当工件旋转周期从较大值逐渐减小时，系统幅值首先逐渐减小，到达鞍-结分岔点时，突然减小为0，达到稳定状态，而系统对应的极限环也随之消失。上述过程中系统幅值的突变会对工件表面产生不可挽回的损害，严重的甚至会发生砂轮表面与工件表面分离的现象，从而产生砂轮与工件之间的严重碰撞。这种情形是非线性磨削模型所特有的，因此研究磨削中的非线性对于优化磨削过程参数具有重要意义。

图4 分岔图

为更加直观地分析系统的稳态与分岔，对于图4中的区域A，当初始进给量取较小值时，作出系统时间历程曲线。如图5(a)所示，此时系统处于稳态磨削过程；而当初始进给量取较大值时，系统时间历程曲线如图5(b)所示，此时系统处于不稳定磨削状态，即发生磨削颤振。

图5 图4中区域A的时间历程曲线

3 磨削颤振抑制

在实际生产过程中，磨削颤振的发生不仅会降低工件加工的表面质量，加剧机床的磨损，而且还会缩短刀具与机床的寿命，增加加工成本。因此，抑制颤振从而提高工件质量和降低加工成本对于企业具有重要意义。

对于大多数主动控制、半主动控制和被动控制方法而言，为抑制颤振，需要在机床上添加额外的辅助部件或者改动机床结构，这样不仅增加了成本，而且所添加的辅助部件可能会降低机床的磨削刚度。而变主轴转速简单易操作，且不需要额外的部件，因此本文作者采用变主轴转速的方法来抑制轧辊磨削加工过程中的颤振。该方法的基本原理是在磨削加工过程中，使主轴转速在所设定的名义转速附近连续或离散地变化，从而破坏颤振产生的条件，达到抑制磨削颤振的目的。连续变主轴转速的公式为

()=+()

(13)

式中：为名义转速；为摄动幅值；()为摄动时间序列。

文中采用混动控制策略来摄动砂轮转速，从而破坏颤振产生的条件，达到抑制磨削颤振的目的。采用洛伦兹方程(Lorez Equations)和若斯勒方程(Rossler Equations)作为混动控制策略的摄动方程。洛伦兹方程为

(14)

为使洛伦兹方程产生混沌现象，普朗特数取10，瑞利数取30，取8/3。

若斯勒方程如式(15)所示，同理，为产生混沌现象，其参数、、取值分别为02、02、57。

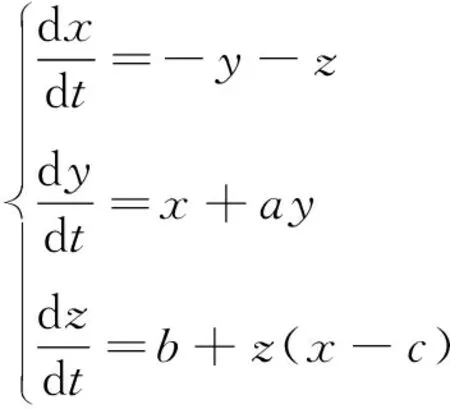
(15)

基于MATLAB中的Simulink模块，采用4阶龙格-库塔法求解洛伦兹方程和若斯勒方程，仿真时间为10 s，将方程解的时间序列作为变时间延迟模块的输入，从而摄动主轴转速，在=5 s时施加混沌控制，混沌控制仿真结果如图6所示。由图6(a)可知，在没有施加混沌控制时，磨削系统拥有较大的幅值，处于颤振磨削状态。而在图6(b)和(c)中，施加混沌控制后，系统的幅值在较短时间内达到稳定值，处于稳定磨削状态。从图6可以看出:文中所采用的洛伦兹方程和若斯勒方程混沌控制策略对于抑制磨削过程中的颤振均有良好的效果，可以提高磨削工件的质量，延长砂轮寿命，降低机床磨损，从而降低成本。

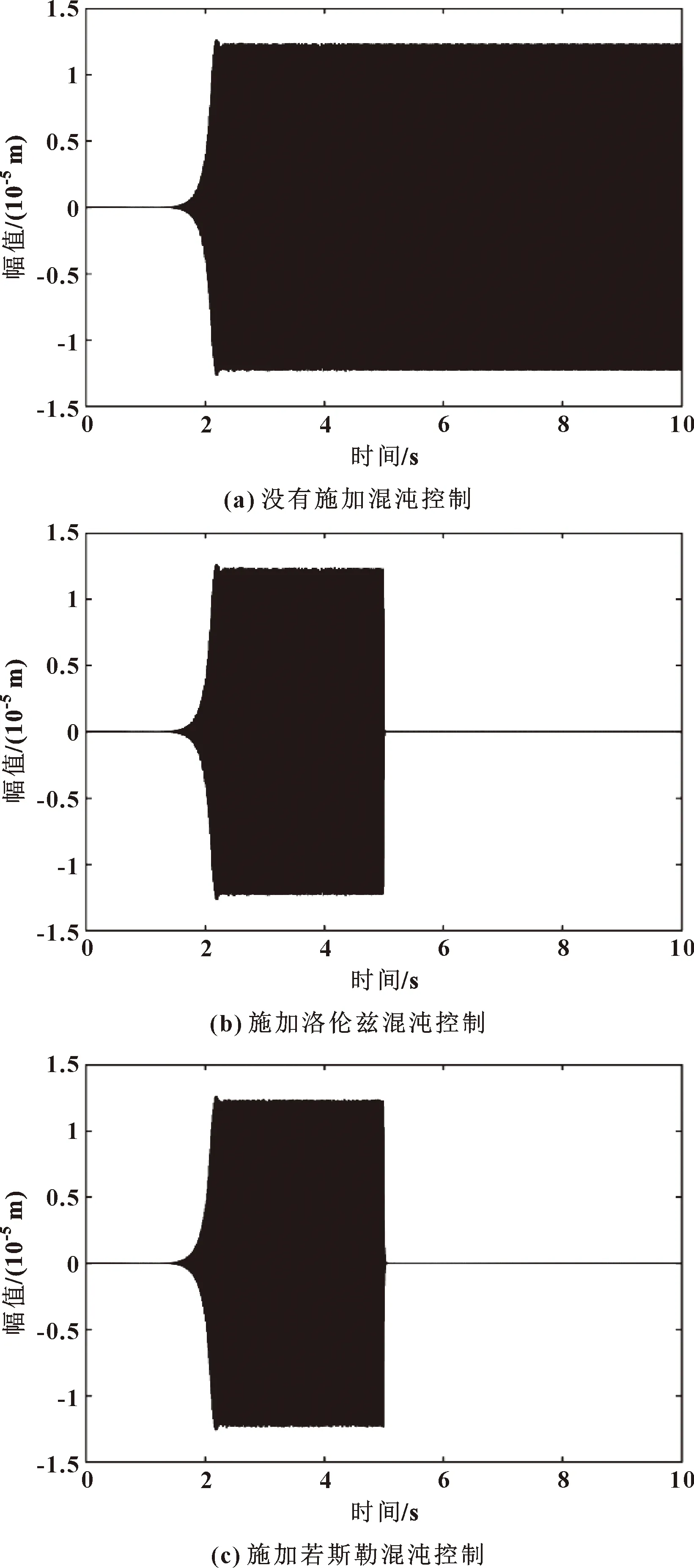
图6 混沌控制仿真时间历程曲线

4 结论

针对稳态叶图边界曲线附近轧辊磨削颤振问题，本文作者通过引入Duffing振子，建立了三自由度非线性磨削动力学模型。基于MATLAB 延迟微分方程工具箱DDEBIF-TOOL，通过数值计算的方法，作出了非线性系统的分岔图，分析了稳态叶图边界曲线附近参数变化对轧辊磨削稳定性的影响。结果表明：当轧辊磨削宽度保持不变时，对于指定区间的工件旋转周期，当它从条件稳态区域进入到稳态颤振区域时，系统发生亚临界Hopf分岔，出现系统幅值跳跃现象，不稳定磨削颤振发生，而对于工件旋转周期位于鞍-结点左边的情形，系统没有发生颤振，说明这一区间的参数可以被用于稳定的轧辊磨削，从而增加了过程参数的选择范围，为实际轧辊磨削加工过程中参数选择提供了参考。为抑制稳态边界曲线附近轧辊磨削中产生的颤振，提出了一种混沌摄动的变主轴转速抑制方法来抑制颤振。时间历程曲线表明，当轧辊磨削系统被施加混沌摄动后，系统的幅值在较短的时间内极大地减小，说明该方法有良好的颤振抑制效果。研究结果为实际加工过程中轧辊磨削颤振抑制提供了一种新的思路。