降噪干扰观测器在机载光电稳定平台上的应用
2022-09-19赵长春胡海升
刘 桉, 赵长春, 胡海升, 张 振
(1.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000; 2.西北工业大学,西安 710000;3.哈尔滨飞机工业集团有限责任公司,哈尔滨 150000; 4.山西文水90队,山西 文水 032000;5.中国人民解放军93126部队,北京 100000)
0 引言
机载跟踪瞄准系统能够对地面目标进行跟踪、捕获、瞄准,可以解算得到目标的位置上报给火控系统,并能通过激光引导导弹打击目标[1]。在机载环境中,为了能清楚地捕获并跟踪地面目标,必须通过光电稳定平台来隔离载机扰动。光电传感器安装在光电稳定平台的框架内,光电稳定平台通过伺服系统控制框架的运动来保持光电传感器视轴的稳定。光电稳定平台框架的控制精度直接影响视轴稳定精度,从而影响光电传感器的成像质量[2]。而机载环境中,控制条件比较恶劣,受到空气风阻、导线牵拉、载机高频晃动等因素的影响,对光电稳定平台框架的机械结构、驱动系统和传感器等都会产生负面影响[3-5]。因此,要求光电稳定平台框架控制系统对扰动和传感器噪声都要具有良好的抵抗能力。
现有的光电稳定平台框架控制系统通常采用干扰观测器[6]和自抗扰控制器[7-8]等来抑制扰动的影响,然而,干扰观测器和自抗扰控制器的加入通常会使系统抵抗噪声的性能下降。有研究人员在使用干扰观测器时,在传感器输出上加入低通滤波器来减弱噪声影响,然而这种解决办法会引起控制系统的不稳定[9]。
针对以上问题,本文在对干扰观测器不足进行分析基础上,根据噪声信号和干扰信号的不同,噪声信号频率较高而干扰信号频率较低的特点,向光电稳定平台控制系统引入了一种新结构的干扰观测器,即降噪干扰观测器[10],使得光电稳定平台控制系统兼顾抗扰性能和抗噪声性能,从而达到了更好的稳定性能。
1 光电稳定平台建模
光电稳定平台伺服系统通常由电流环、速度环和位置环三环控制。电流环通过电流传感器实现对电机电流的闭环;速度环通过陀螺仪测量光电稳定平台各框架相对惯性空间的速度,通过对该速度进行闭环,能够控制框架相对惯性空间的稳定,是实现光电稳定平台隔离载机扰动的主要环节,也被称为稳定环;位置环通过位置传感器或者图像机返回的脱靶量对平台各框架的位置进行闭环。由于稳定环对平台隔离载机扰动具有重要作用,因此本文主要对稳定环进行研究。稳定环的控制框图见图1。

图1 光电稳定平台稳定环控制框图Fig.1 Control block diagram of stabilization loop of electro-optical stabilized platform
其中:ω是实际转速;ωd是指定转速;id是稳定环控制器输出的指定电流;ie是电机的实际电流;kP是PWM系数;L是电机电感;s是传递函数参数;R是电机电阻;Ke是电机反电动势系数;KT是电机转矩系数;J是框架与电机的转动惯量。
由于电流环的带宽比稳定环要高很多,因此可以把电流环等效为一个一阶惯性环节[11],即
(1)
式中,Ti表示电机电气常数。
由刚体动力学可知
(2)
式中,Kf是等效摩擦系数。
根据式(1)和式(2)可得到,稳定环控制对象的传递函数为
(3)
2 传统干扰观测器(DOB)及其性能分析
图2所示为传统干扰观测器(DOB)的控制框,为了分析DOB的性能,需要考虑指令输入r、外界干扰d和传感器噪声n对输出y的影响。

图2 传统干扰观测器控制框图Fig.2 Control block diagram of traditional disturbance observer
其中,C,Q,P分别代表相应环节的传递函数,u代表图上相应位置的信号,即C(s)是控制器的传递函数,Q(s)是滤波器,P(s)是控制对象的传递函数,Pn(s)是控制对象辨识出来的的标称模型,通常会与P(s)有差别,但是差别应该很小。设输出y与r,d,n的关系为y(s)=Gyr(s)r(s)+Gyd(s)d(s)+Gyn(s)n(s),根据图1可以推导出
(4)
(5)
(6)
Gyr表示指令输入r对输出y的影响,由于Pn和P在正常情况下差别应该很小,可以认为P-Pn≈0,那么有
(7)
可见Gyr主要受到控制器C(s)的影响,可以通过调整控制器的结构和参数使得指令输入r有比较好的响应。
Gyd表示外界干扰d对输出y的影响,同样有
(8)
可见Gyd受到控制器C(s)和滤波器Q(s)的影响,可以通过调整控制器和滤波器的结构和参数使系统对干扰具有较好的抵抗能力。
Gyn表示传感器噪声n对输出y的影响,考虑到噪声的频率一般比较高,这时Q≈0,同时仍然有P-Pn≈0,可得
Gyn=-(PC)/(1+PC)
(9)
可以看到式(9)和式(7)的幅频特性曲线是相同的,只是正负号不同,这说明在使用DOB的情况下,要想使系统既有较好的指令输入响应,又有较好的噪声抑制能力是不可能的。
3 降噪干扰观测器及其性能分析
由上节可知,DOB不能抑制噪声,为了进一步分析可以将图2转换为图3,并可得
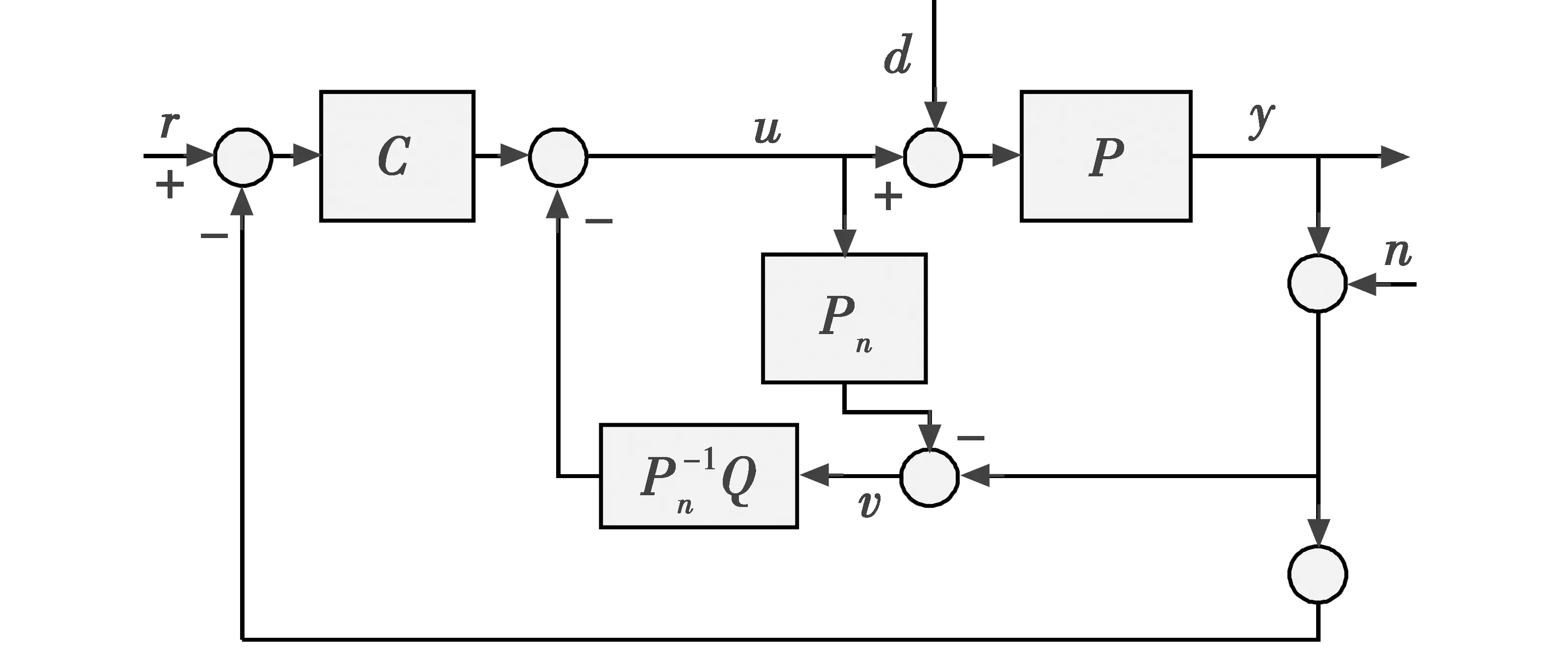
图3 转换后的传统干扰观测器控制框图Fig.3 Control block diagram of traditional disturbance observer after conversion
v=y+n-uPn
(10)
系统输出y可以表示为
y=(u+d)P
(11)
所以有
v=u(P-Pn)+dP+n
(12)
可见v由三项构成,即vp=u(P-Pn),是建模误差影响,vd=dP,是外部扰动影响,vn=n,是噪声影响。
vd体现为外部扰动影响,实际中主要成分是低频,在控制系统中应该被抵消掉,DOB就是做这样的工作。
vp体现为建模误差影响,实际中主要是高频的结构谐振,控制系统应该减少对vp的响应以避免激发谐振。
vn体现为噪声影响,实际中也主要是高频成分,控制系统也应该减少对vp的响应以提高精度。
根据以上分析可知,DOB只对vd进行了处理,对另外两项并没有改善。为了提高DOB的性能,本文对DOB做了改进,如图4所示。

图4 降噪干扰观测器控制框图Fig.4 Control block diagram of noise reduction disturbance observer

改进后的DOB可称为降噪干扰观测器,既能提高系统抗扰能力,又能提高系统降噪能力。下面用较为严格的理论来证明。同样设输出y与r,d,n的关系为
y(s)=Gyr(s)r(s)+Gyd(s)d(s)+Gyn(s)n(s)。
根据图2可推导出
(13)
(14)
(15)
同样,如果认为P-Pn≈0,那么
(16)
与传统DOB的效果相近。
式(14)、式(15)中,令P=Pn,得
(17)
(18)
Gyd对频率低的干扰d起作用,当频率较低时,Q≈1,只要满足
CFPn≈0
(19)
就能对干扰进行有效抑制。
Gyn对频率高的噪声n起作用,当频率较高时,Q≈0,F≈1,只要满足
CFPn-CPn=CPn(F-1)≈0
(20)
就能对噪声进行有效抑制。
所以通过选择合适的低通滤波器Q和高通滤波器F,可使降噪干扰观测器(Noise Reduction Disturbance Observer,NRDOB)对干扰和噪声都有较好的抑制能力。
4 控制系统设计
根据式(3)推导的模型和实际测量,光电稳定平台框架的传递函数为
(21)
其带宽是39 rad/s,幅频特性曲线如图5所示。

图5 控制对象幅频特性曲线Fig.5 Amplitude-frequency characteristic curve of control object
实际获取到的模型会与真实模型存在一定程度上的偏差,设标称模型为
Pn(s)=0.95/[(0.001 2s+1)(0.022s+1)]。
(22)
稳定环控制器采用PI控制器,即
(23)
设定Gyr的带宽为80 rad/s,相位裕度为60°,可得kp=1.51,ki=121.4。
最后,NRDOB设计的关键是选择合适的低通滤波器Q和高通滤波器F。选择Q的形式为
Q(s)=(τs+1)-4
(24)
式中,τ表示干扰系数。Q的截止频率为
ωc=0.435/τ
(25)
高通滤波器F可以选为
F=1-Q
(26)
那么可得
Gyd≈P(1-Q)
(27)
Gyn=Q
(28)
根据式(27)和式(28)可知:ωc越大,系统对干扰的抵抗能力就越强,但是对噪声的抵抗能力就越弱;ωc越小,系统对干扰的抵抗能力就越弱,但是对噪声的抵抗能力就越强。根据式(19)为了使系统对干扰有较强的抵抗能力,应该使Q的截止频率大于P的带宽,所以ωc>39,τ<0.011。
取τ分别为0.01,0.005和0.002 5时,系统对干扰的幅频特性曲线如图6所示。

图6 系统对干扰的幅频特性曲线Fig.6 Amplitude-frequency characteristic curve of the system to interference
由图6可见,低频下τ越大,衰减越小,高频下3条线汇合。根据式(27),Gyd相当于被控对象P串联一个高通滤波器1-Q,所以低频下受Q时间常数τ的影响明显,τ越大,1-Q的截止频率越低,Gyd的低频衰减就越小。高频下,1-Q≈1,所以高频下的幅频特性曲线都趋近于被控对象的幅频特性曲线。
取τ分别为0.01,0.005和0.002 5时,系统对噪声的幅频特性曲线如图7所示。
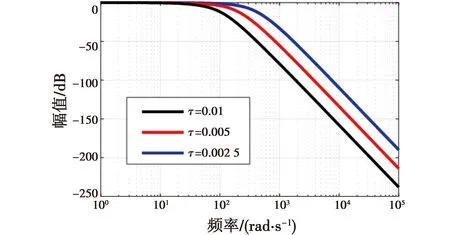
图7 系统对噪声的幅频特性曲线Fig.7 Amplitude-frequency characteristic curve of the system to noise
由图7可见,高频下τ越大,衰减越大,低频下3条线都重合到0 dB线上。根据式(28),Gyn相当于一个低通滤波器,τ越大,Q的截止频率越低,对噪声衰减就越大。
为了使系统兼顾抗扰性能和抗噪性能,可以选择τ的值在0.005左右。
5 控制系统仿真
为了验证理论分析,在Simulink下搭建了光电稳定平台框架的仿真模型,如图8所示。

图8 控制系统的Simulink仿真模型Fig.8 Simulink simulation model of the control system
图8中,指令输入r为单位阶跃信号,干扰信号d为幅值为0.1 rad/s、频率为3 rad/s的正弦信号,噪声信号是均值为0 rad/s、方差为0.03 rad/s的随机信号。
图9所示为正弦扰动下DOB与NRDOB的控制输出效果对比。
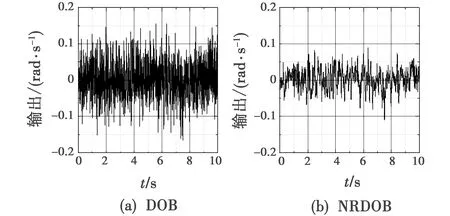
图9 正弦扰动下DOB与NRDOB的控制输出效果对比Fig.9 Control output effect comparison between DOB and NRDOB under sinusoidal disturbance
由图9可以看到,使用NRDOB输出噪声影响明显小于DOB。经过计算,DOB输出均方根为0.044 rad/s,NRDOB输出均方根为0.029 rad/s。
一些非线性因素会出现干扰剧烈变化的情形,为了体现这些情形对控制效果的影响,将干扰源换成幅值为0.1 rad/s、频率为1 Hz的方波信号,DOB与NRDOB的控制输出效果对比如图10所示。
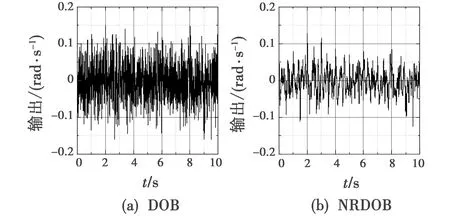
图10 方波扰动下DOB与NRDOB的控制输出效果对比Fig.10 Control output effect comparison between DOB and NRDOB under square wave disturbance
由图10可以看到,在方波扰动下NRDOB输出噪声影响也明显小于DOB。通过计算,DOB输出均方根为0.045 rad/s,NRDOB输出均方根为0.032 rad/s。
6 结论
为了提高稳定平台对干扰和噪声的抵抗能力,本文设计了一种降噪干扰观测器。首先分析了干扰观测器的原理和不足,然后针对干扰观测器的不足与干扰信号和噪声信号的特点分析了降噪的原理,提出了降噪干扰观测器,并使用降噪干扰观测器,设计了光电稳定平台框架的控制系统。仿真实验结果表明,使用降噪干扰观测器后,系统同时具有良好的抗扰和抗噪能力。正弦扰动下,输出均方根由0.044 rad/s下降至0.029 rad/s,方波扰动下,输出均方根由0.045 rad/s下降至0.032 rad/s。由此说明降噪干扰观测器能够提高光电稳定平台的性能。
