基于时频能量对消的跳频信号参数盲估计

姚志成， 侯 范， 杨 剑， 王海洋， 王自维

(火箭军工程大学，西安 710000)

0 引言

跳频(Frequency Hopping,FH)通信因其具有较强的抗多径、抗干扰、抗截获、易组网能力而被广泛应用于现代军事和民用通信系统[1-3]，但随着电磁环境的日益复杂，对跳频信号的检测和参数估计已成为通信对抗领域的重点问题[4]。如何有效地从背景噪声和干扰信号中检测出跳频信号并进行参数估计继而实现干扰反制变得愈加困难[5]。

目前，针对跳频信号的参数估计方法主要包括图像处理法[5-7]、稀疏重构法[8-10]以及时频分析法[11-16]3种。其中，图像处理法与稀疏重构法都存在运算复杂、计算量大的问题，故而基于时频分析的参数盲估计方法应用最为广泛。文献[11-13]首先对接收信号进行时频变换并提取时频脊线，再利用小波变换的奇异点检测性能找出跳变时刻，进而估计出跳频信号周期和跳速；文献[14]通过提取时频矩阵中的每一时刻能量最大值得到近似周期性函数，再对该函数进行FFT运算，峰值频率即为跳频速率估计值，其倒数即为跳频周期估计值；当存在定频干扰时，文献[11-14]算法均难以实现跳频信号的参数估计；文献[15-16]首先通过遗传算法或者迭代处理选取自适应阈值，对时频矩阵进行截断处理与重构，再利用K-means聚类算法找出定频干扰并去除，最后使用小波变换求得跳频周期与跳速，该算法虽然实现了定频干扰条件下跳频信号的参数估计，但是增加了计算复杂度；文献[17-19]通过功率谱的分段对消去除定频干扰，但是分段数对算法的对消性能有较大影响，为了得到较好的性能就需多次计算分段谱以及分段前整段信号的功率谱,计算复杂度较高。

综上所述，现有算法均不能很好地解决噪声和定频干扰对跳频信号参数盲估计所带来的问题，因此，本文在文献[17-19]频域功率谱对消算法去除定频干扰思想的基础上进一步展开研究，通过分析时频矩阵中跳频信号与噪声和定频干扰能量对消的差异性，利用K-means对能量对消差值进行聚类选取自适应阈值，实现噪声和定频干扰的同步去除，最后利用最小二乘法线性拟合实现对跳频周期等参数的盲估计，提高了估计精度，具有一定的工程应用价值。

1 信号预处理

1.1 信号模型

假设有一个跳频信号，该跳频信号的数学表达式为[20]

(1)

式中：k为整数，k≥1;Th为跳频周期;t表示采集信号时间；A为信号幅度；θ为初始相位；fk为第k个时隙的跳频频率；rTh(t)表示矩形窗，且满足

(2)

一般情况下，由于跳频带宽较宽，跳频频率分布较广，因此在接收机接收到的信号中往往极易出现同频段的定频干扰和高斯白噪声，则接收信号模型为[4]

x(t)=s(t)+J(t)+n(t)

(3)

式中：J(t)表示定频干扰信号；n(t)为加性高斯白噪声。

1.2 时频分析

时频分析可以清晰地反映跳频信号的时频特性，因而被广泛应用。目前，时频变换算法主要有短时傅里叶变换(STFT)[21]、魏格纳分布(WVD)[22]和小波变换(WT)[23]。由于STFT算法运算量最少，更具有实时性[21]，因此本文选取STFT算法作为时频分析工具。

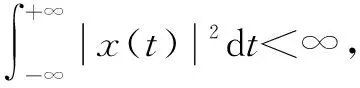
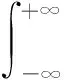
(4)

式中:ω(τ,t)表示窗函数，τ表示时延量;TSTFT(t,f)表示信号x(t)时间和频率的二维分布。

清晰的时频图是实现跳频信号参数估计的重要保证，而定频干扰的存在使得跳频信号被湮没，给跳频信号的提取检测和参数估计造成很大的麻烦[4]，因此,有效地去除定频干扰是进行参数估计的必要条件。

2 算法描述

2.1 能量对消去除定频干扰

清晰的时频图是进行参数估计的重要前提，因此，须去除噪声和定频干扰的影响。假设信号经过STFT后产生的M×N时频矩阵表示为TSTFT(i,j)，时频矩阵阈值为T，将矩阵中大于阈值的元素保留，小于等于阈值的置0，则有

(5)

式中，i和j分别表示时频矩阵的第i行和第j列，且1≤i≤M,1≤j≤N。

由式(3)可知，接收机实际接收信号主要包含跳频信号、定频干扰和加性高斯白噪声3种。其中，跳频信号与定频干扰只存在于特定频点，高斯白噪声在整个时频段内均有分布。文献[17-19]通过功率谱对消去除定频干扰时，假设其一直存在且截取连续，则理论上因为其平稳特性，信号在不同时刻的功率谱相同，因此认为，定频信号在整个时间段上的平均功率谱与各段功率谱基本一致[17]。本文基于相关功率谱对消思想，在时频图上进行能量对消，再通过K-means聚类算法选取自适应阈值，进行时频矩阵的重构。

在时频矩阵中，每一行即代表对应每一频率在整个接收时间内的能量变化，因此首先对整个时频矩阵逐行求平均，即

(6)

式中，S(i)表示时频矩阵第i行的均值，i=1,2,…，M。

在接收信号中，定频干扰与噪声存在于整个时间段内，所以，其时频矩阵能量均值与每一时刻能量值相差不大；对于跳频信号，由于其每一频率只存在一段时间，在整个时间段内频率不断跳变，所以，其在对应频率上的时频能量均值远小于每一时刻能量值。

选取时频矩阵中每一频率分量的最大值与该行均值进行差值运算，即

Sd(i)=TSTFT(i,m)-S(i)

(7)

式中：Sd(i)表示第i行最大值与其均值的差值，在下文中均用差值代替；TSTFT(i,m)表示第i行的最大值。

将各差值组成一个新的向量，即

K={Sd(1),Sd(2),…，Sd(M)}。

(8)

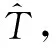
(9)

通过式(9)对时频矩阵初步截断处理：当时频矩阵每一行的差值小于等于阈值，即说明该行对应频率不存在跳频信号，故将其全部元素置0；当差值大于阈值时，元素全部保留。此时,时频矩阵中跳频频率部分噪声依然未被滤除，对该部分每一个元素求差值，并同阈值进行比较，大于阈值部分为跳频信号数据保留，小于等于阈值部分置0，则对原始时频矩阵的截断处理为

(10)

2.2 跳频信号参数估计

对于重构时频矩阵来说，计算其在每个时刻的最大值[14]，如图1所示。

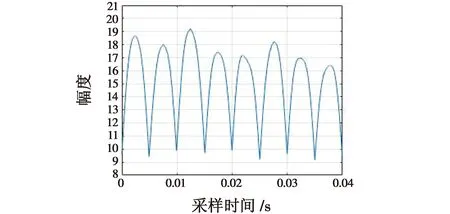
图1 最大时频值包络图Fig.1 Envelope diagram of the maximum time-frequency value

由图1可知，最大时频值包络具有周期性，文献[14]通过傅里叶变换求得频谱，其峰值即为跳速，跳速的倒数为跳频周期。文献[14]算法忽略了噪声存在对包络提取所造成的微小误差，因此估计精度较低。可以提取包络每个周期的波峰、波谷所处时间，并利用最小二乘法线性拟合，减少噪声带来的误差。

对波峰、波谷所处时间进行提取，并且去除首尾两个时间之后依次用ti表示，i=1,2,…，n。利用最小二乘法对ti进行线性拟合，即

t′=a+b×i

(11)

式中：t′表示提取波峰、波谷的时间；a表示直线截距;b表示直线斜率；i表示对采样时间的第i次提取;

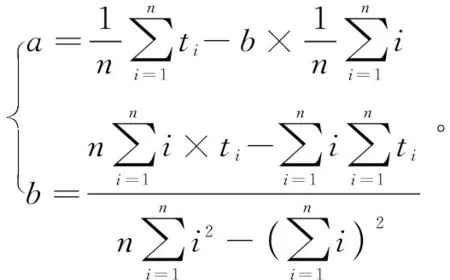
(12)

图2所示为时间线性拟合。

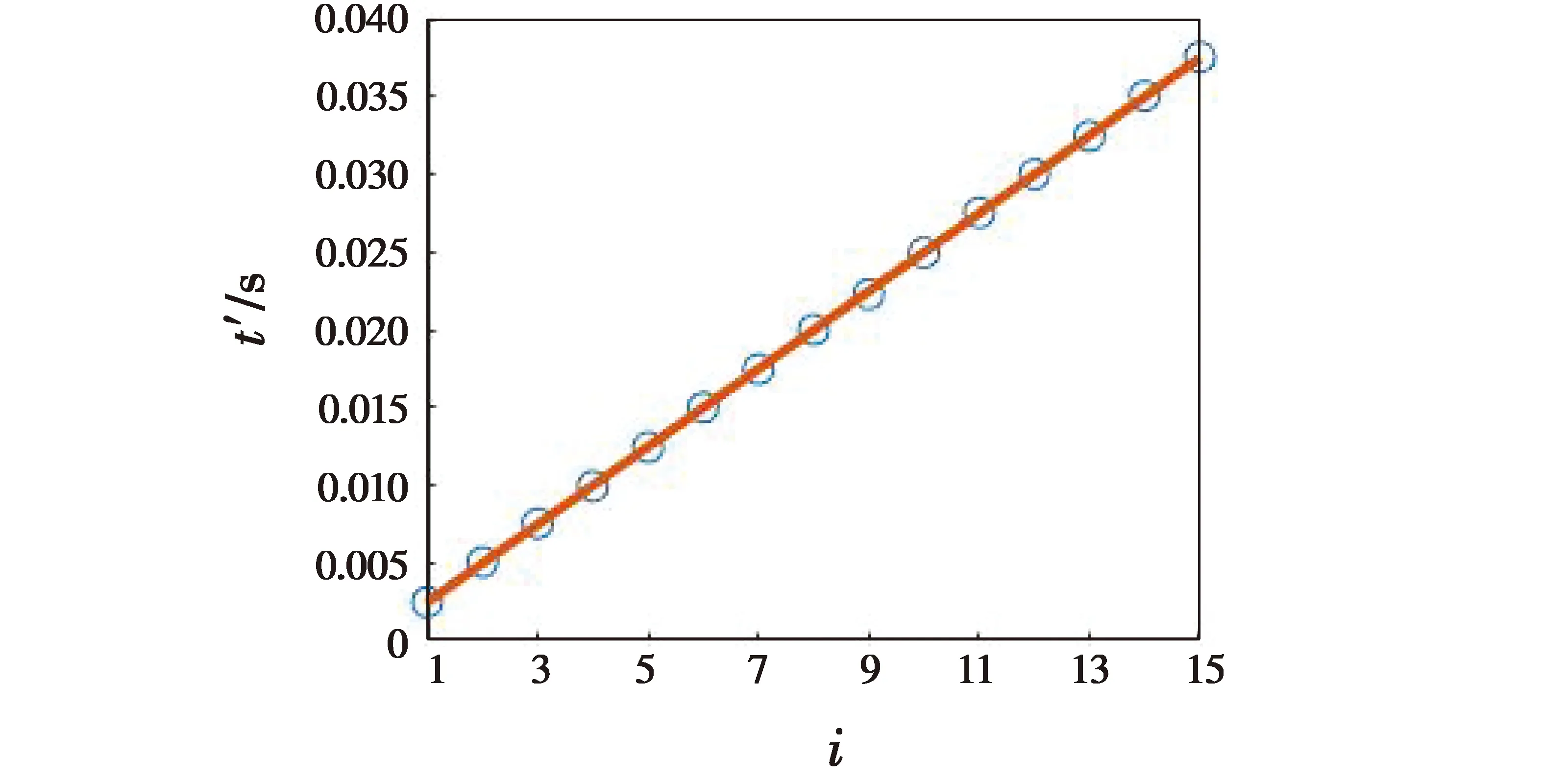
图2 时间线性拟合图Fig.2 Time linear fitting diagram

设跳频周期为Th，则

(13)

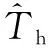
由于已经估计出跳频周期，其倒数即为跳速，即

(14)

记第1跳起跳时间(即第2跳起始时间)为T0，则其估计值为

(15)

2.3 算法流程

本文所提算法的步骤如下：

1) 计算接收信号的STFT，得到对应的时频矩阵；

2) 基于时频能量对消和K-means聚类选取自适应阈值，截断处理得到新的时频矩阵；

3) 计算重构后时频矩阵每个时刻t′的最大时频值，得到近似周期性的时频值包络图；

4) 提取包络图各周期内波峰波谷所在的时刻ti；

5) 通过最小二乘法对(i,ti)线性拟合，得到其斜率并计算跳频周期；

6) 根据估计得到的跳频周期对跳速和第1跳起跳时间进行估计。

3 仿真实验与分析

为验证本文算法的有效性，设计了以下仿真实验。

3.1 实验1

无频率碰撞时，对本文时频矩阵截断处理算法进行仿真验证。根据式(1)产生一段跳频信号，包含了8个跳频周期，跳频频率集为{0.025,0.01,0.125,0.075,0.175,0.15,0.2,0.05}，单位为MHz，跳频周期为5 ms；定频干扰为0.25 MHz，STFT采用长度为512的Hamming窗，采样频率为10 MHz，信噪比(SNR)为-5 dB，干信比(ISR)为0 dB。接收信号经STFT之后的时频图见图3。

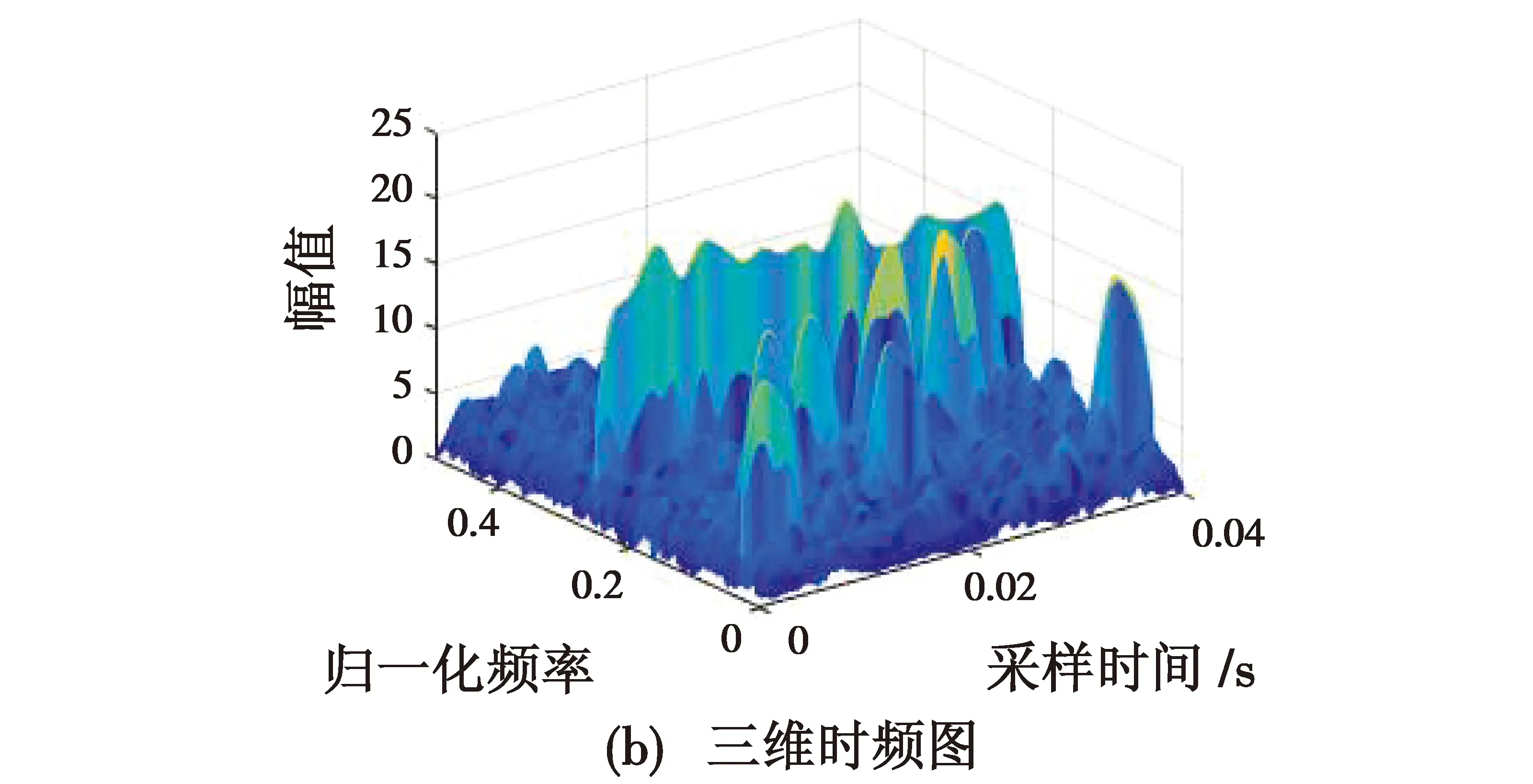
图3 接收信号无频率碰撞时频图Fig.3 Time-frequency diagram of received signal without frequency collision

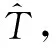
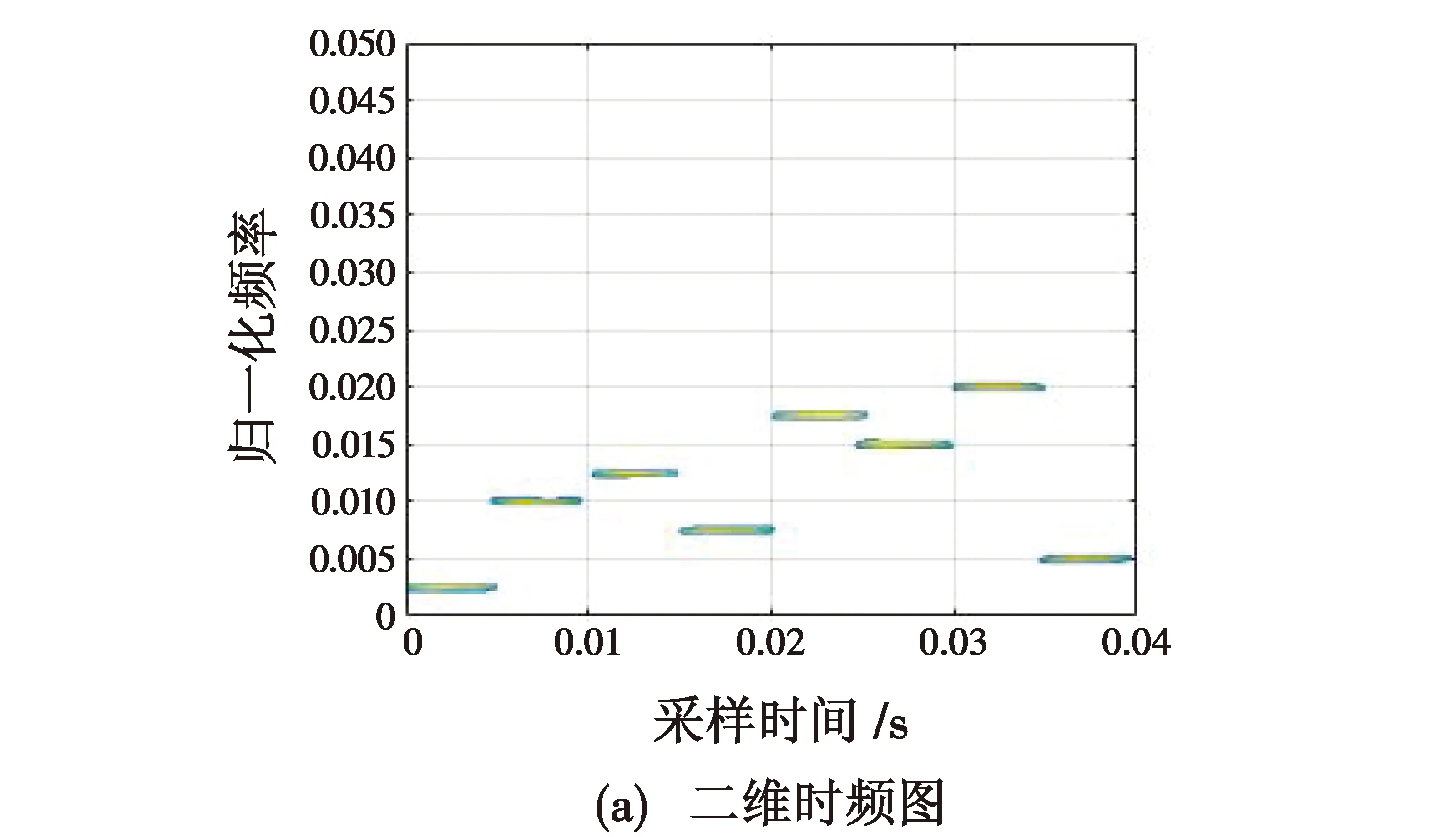
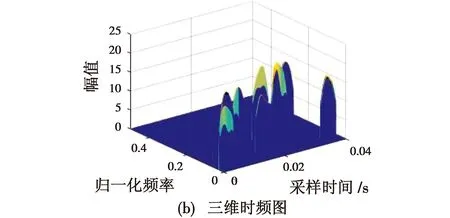
图4 接收信号无频率碰撞截断处理后时频图Fig.4 Time-frequency diagram of the received signal without frequency collision after truncation processing

由图4可以看出，本文截断处理算法较好地消除了定频信号的干扰，并且保持了原始信号中的跳频成分。

3.2 实验2

发生频率碰撞时，对本文时频矩阵截断处理算法进行仿真验证。取定频干扰为0.15 MHz，其他仿真条件与实验1相同。接收信号经STFT之后的时频图见图5。

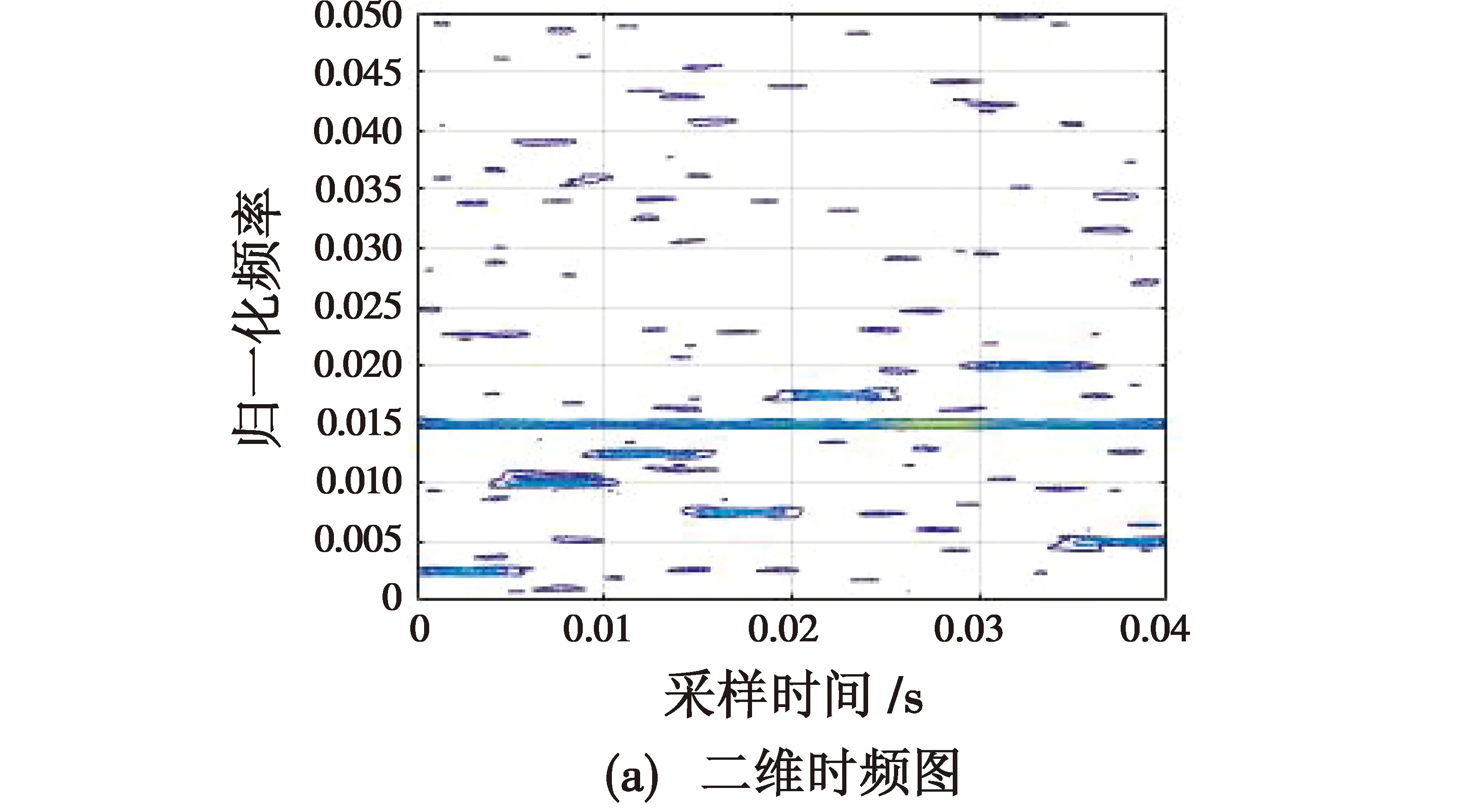
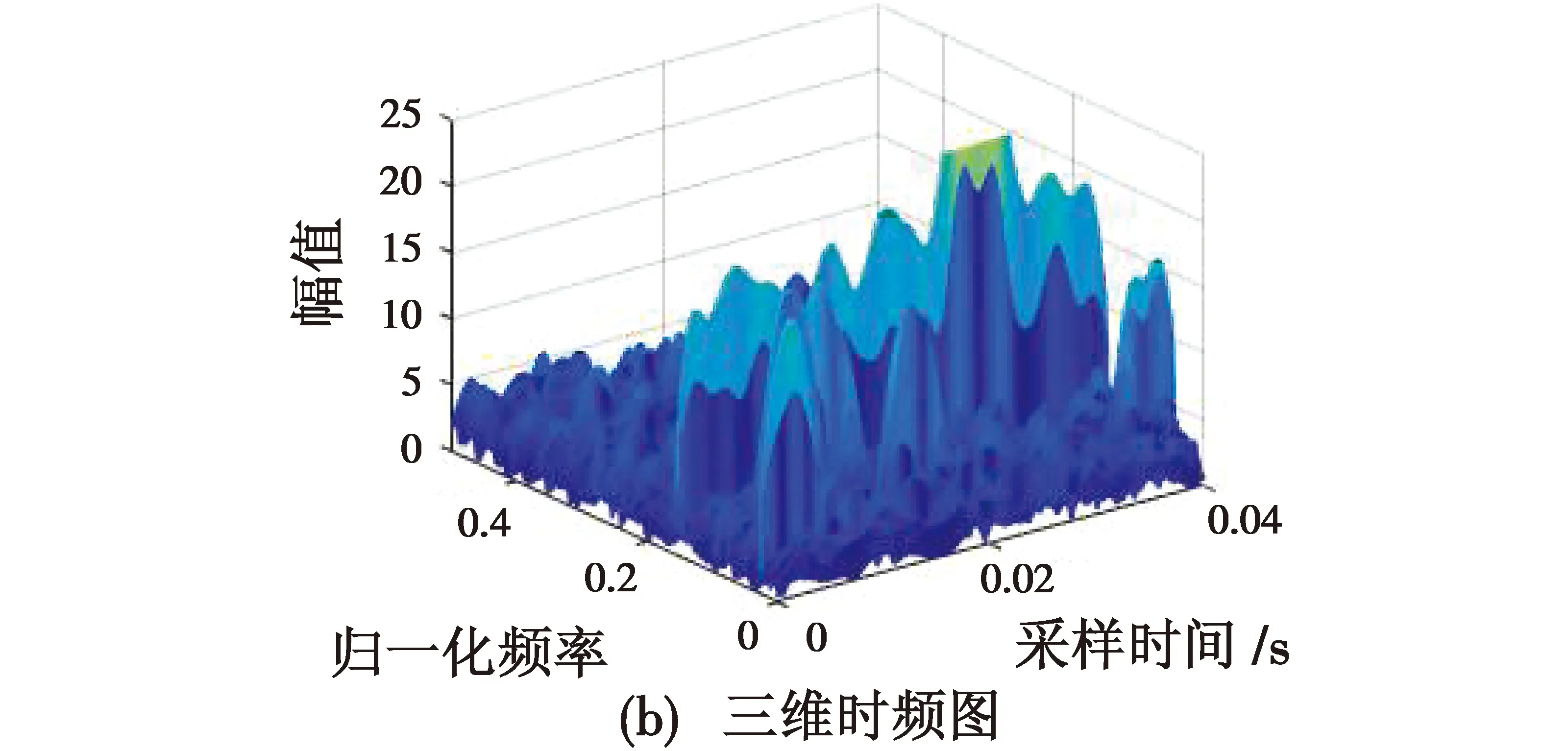
图5 接收信号发生频率碰撞时频图Fig.5 Time-frequency diagram of received signal with frequency collision

由式(6)-式(10)确定自适应阈值之后对TSTFT(i,j)矩阵进行截断处理，消除定频干扰，结果如图6所示。

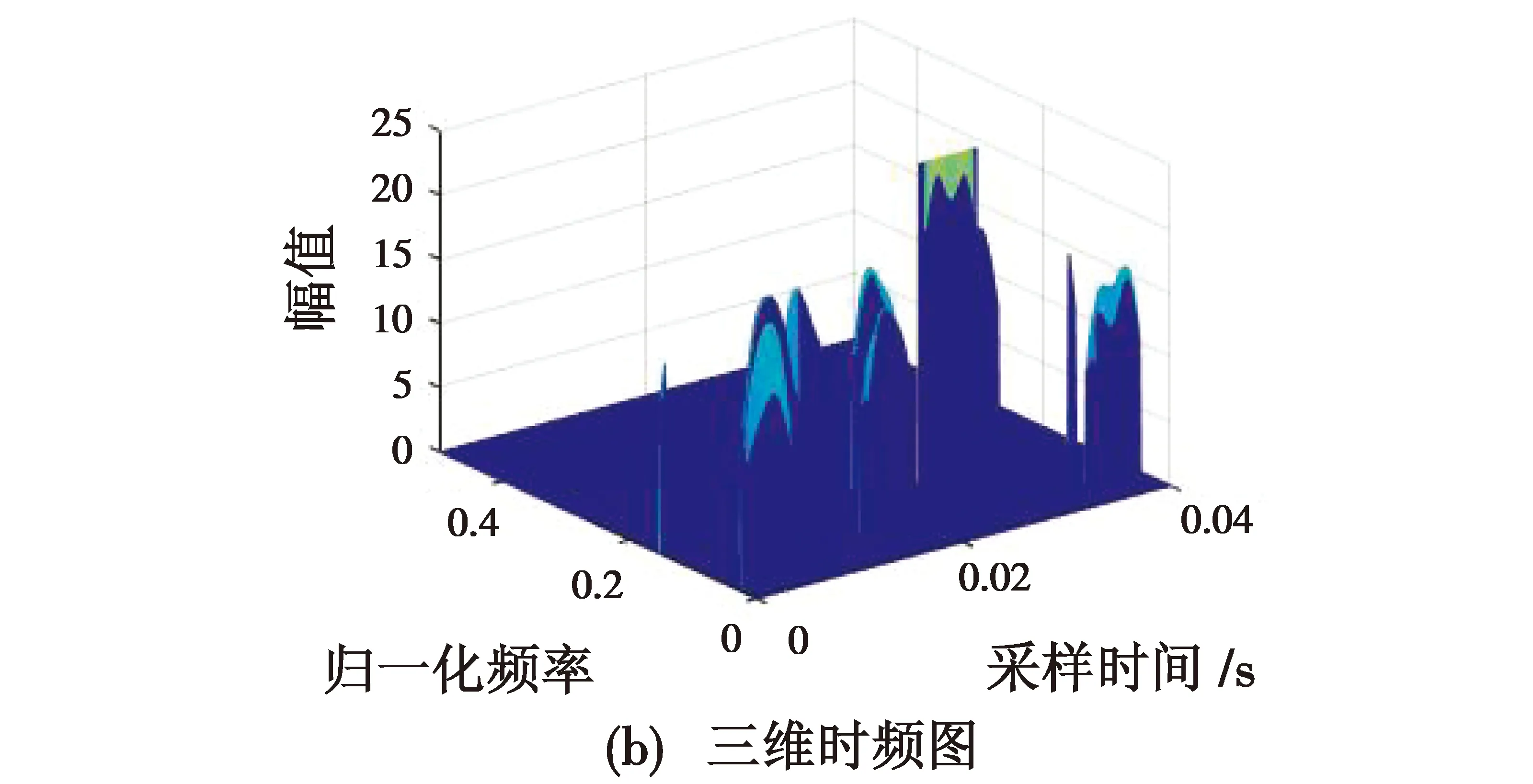
图6 接收信号发生频率碰撞截断处理后时频图Fig.6 Time-frequency diagram of received signal with frequency collision after truncation processing

由图4和图6可以看出，本文所提算法很好地实现了定频干扰的去除。当发生频率碰撞时，碰撞频率处能量值为定频信号与跳频信号能量值的叠加，因此，通过所提出的截断处理算法在消除定频信号中未碰撞部分的同时，使得保留的跳频信号部分能量值远高于其他跳频频率能量值，但是跳频信号的完整提取保留，依然为参数估计提供了必要的依据。

3.3 实验3

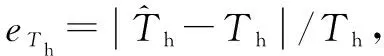
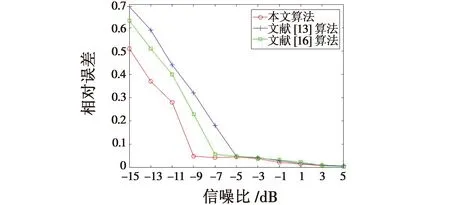
图7 跳频周期估计相对误差Fig.7 Relative error of frequency hopping period estimation

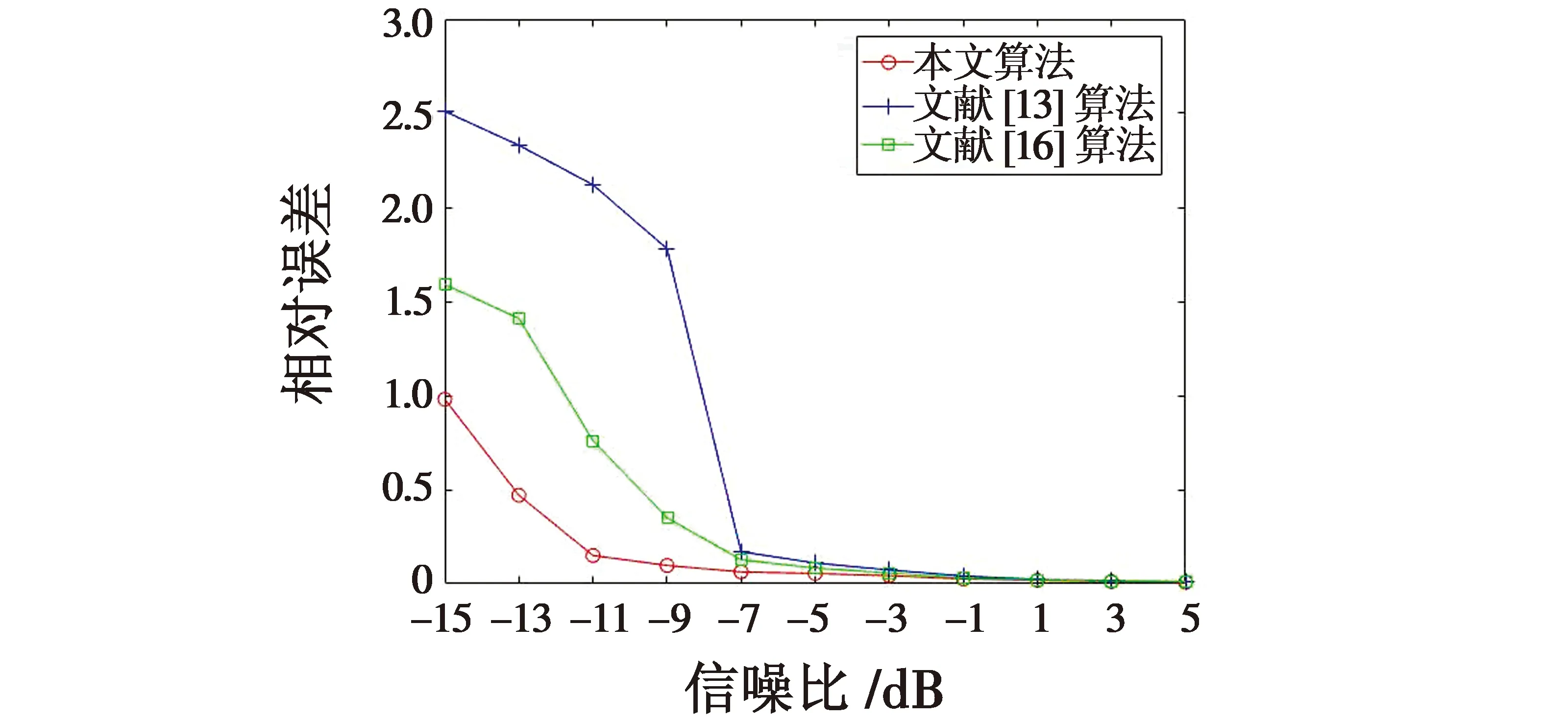
图8 起跳时间估计相对误差Fig.8 Relative error of take-off time estimation

由图7可知：文献[13]对接收信号直接进行时频分析处理，只能在没有定频干扰且信噪比为-5 dB条件下才能得到清晰的时频脊线，进而实现跳频周期的估计；文献[16]算法在文献[13]算法基础上进行改进，通过迭代处理去除噪声，并且基于K-means聚类消除了定频干扰的影响，当信噪比大于-7 dB时，跳频周期相对误差在0.05以内，提升了原有算法的精度；本文算法通过K-means选取自适应阈值以及基于功率谱对消思想实现了噪声与定频干扰的同步去除，使得跳频信号在大于-9 dB时被检测到的概率达到90%，进而使得跳频周期的相对误差保持在0.05以内；同时，当信噪比小于-9 dB时，以牺牲跳频信号的部分边缘信息为代价去除噪声和定频干扰，提取出部分跳频信号，依然可以实现参数的估计，但是精度被降低。

由图8可知:当信噪比大于-5 dB时，3种算法起跳时间的估计精度基本一致；当信噪比小于-5 dB时，由于本文算法在进行参数估计时选取的数据约为文献[13]、文献[16]算法数据的2倍，因此跳频周期估计精度有所提高，使得起跳时间的估计相对误差同步减小。同时，由于本文算法在信噪比小于-9 dB条件下依然可以发现并提取跳频信号进而实现跳频周期的参数估计，所以使得对起跳时间的估计误差依然远小于文献[13]和文献[16]算法，使得在信噪比为-11 dB时对起跳时间的估计误差依然可以在0.15以内。

3.4 实验4

当定频干扰功率不同时，验证其对跳频周期估计结果的影响，定义估计相对误差eTh小于1%时为一次准确估计。仿真条件与实验1相同，在信噪比为-15～5 dB的条件下对0～10 dB干信比范围内每组数据进行500次蒙特卡罗实验，得到各个干信比条件下的估计准确率，结果如图9所示。

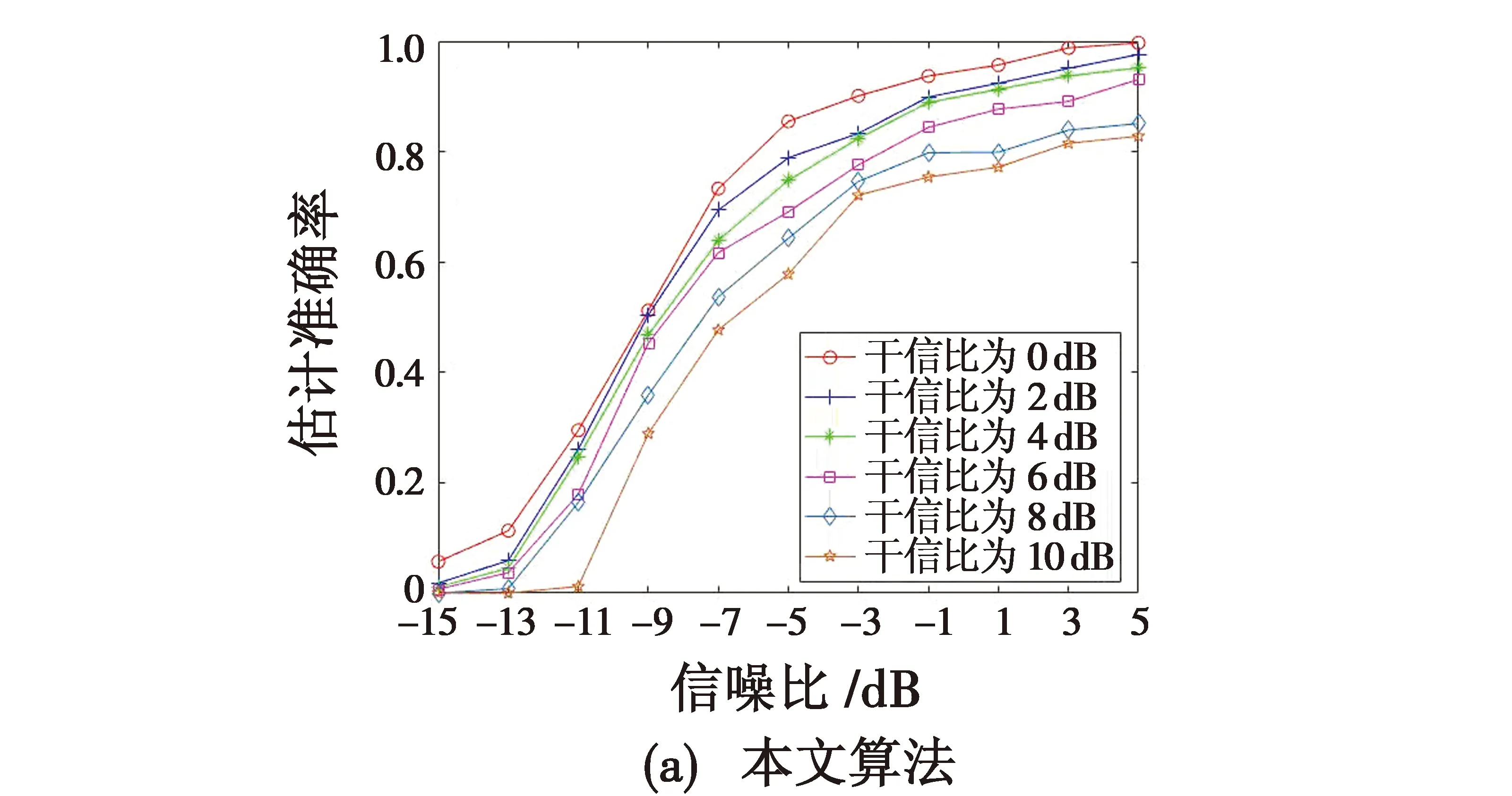
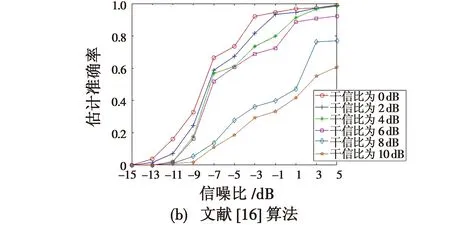
图9 不同干扰功率下跳频周期估计准确率Fig.9 Accuracy in estimating frequency hopping periods under different interference powers

由图9可知，2种算法对跳频周期的估计准确率均随着干扰功率的增强而降低，文献[16]算法首先在整个时频矩阵中进行迭代选取阈值，使得阈值偏大，造成部分信号的缺失，从而降低了估计准确率，当干信比大于6 dB时，情况进一步恶化，使得估计准确率骤降。本文算法是基于能量差值进行阈值选取，降低了干扰信号所产生的影响，提高了跳频周期的估计准确率。

综上所述，本文算法具有更好的抗噪性和抗干扰能力，对跳频参数的估计优于原算法。

4 结束语

本文基于时频能量对消思想，采用K-means聚类方法选取自适应阈值同步去除噪声和定频干扰，并对每一时刻沿频率轴的能量最大值进行包络提取，最后利用最小二乘法对所提取包络的每一周期内波峰波谷对应的时刻进行线性拟合，从而,在没有任何先验信息的情况下实现对跳频信号跳频周期、跳速和起跳时间等参数的盲估计。本文算法解决了定频干扰存在时跳频信号的参数估计问题，并且有效提高了算法的抗干扰能力。但是本文算法只针对简单场景下单个跳频信号的情况进行分析处理，而现代战争中多个跳频通信同时存在的情况必然随处可见，同时解决多个跳频通信的参数盲估计问题将是后续的主要研究方向。