基于变换域分形的海面小目标快速检测

尹鹏智, 戴恩泽

(中南大学自动化学院，长沙 410000)

0 研究背景及难点

在海杂波领域的60多年研究进程中，科研工作者取得了较大的研究进展与成果。现代雷达信号处理中的目标回波信号可近似为线性调频信号(Chirp)，而待分数阶傅里叶变换 (FRFT)[1]处理后，在特定变换阶次下(即最优阶次)目标信号会在分数域形成明显的冲击，目标回波的能量聚集使得信杂比得到改善。反观纯海杂波在分数域内能量无法形成有效的聚集，因此有学者提出利用FRFT改善雷达回波的信杂比后再进行分形检测[2-3]。 文献[2-4]在海杂波FRFT域的分形特征分析上取得了一定成果，且文献 [5-7]利用FRFT域的多重分形特征进行目标检测取得理论层面突破。但FRFT算法思路应用于实际工程仍有较大的困难，难点在于FRFT变换时需要先选取最优阶次，需要较大的计算量[1]，且传统的多重分形去趋势波动分析(MFDFA)算法[8]性能不够稳定。本文选取FRFT算法优化了最优阶次的寻优过程，且改进了传统MFDFA算法，提出了基于FRFT域分形的海面小目标快速检测算法。海杂波中,尤其是低信杂比下的微弱目标检测作为一个研究难点，在民用与军用领域都具有重要意义。海面小目标的雷达反射截面(RCS)较小，雷达目标回波常被强海杂波淹没[9-10]，该算法具有广阔的应用前景。

1 变换域分形检测基本算法

1.1 基于FRFT的检测原理

FRFT[1]常用于信号处理， Chirp信号的检测与参数估计是其中一种典型应用。早在1993年已经有学者验证了FRFT与Wigner-Vile分布(WVD)的内在联系，Chirp信号在WVD分布的时频面上能量聚集为一条直线，FRFT利用时频面的坐标轴旋转，使得线性调频信号在时频面上的能量直线聚集，最终在FRFT变换后实现能量聚集，雷达回波经过FRFT变换后实现了能量聚集，提高了回波信号的信杂比，有利于后续的目标检测。

信号x(t)的FRFT变换的具体定义为

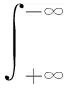
(1)

式中：u为变换域频率；α为变换旋转角度，α=pπ/2，p为变换阶次；核函数Kα(u,t)表达式为

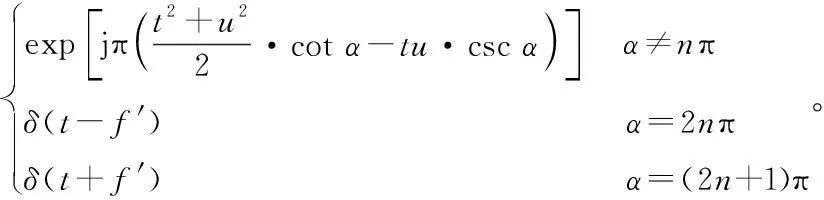
(2)

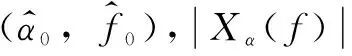
(3)

1.2 最优阶次快速估计算法

在一定时间内，Chirp信号的频率具有明显线性规律，信号带宽与信号持续时长具有线性比例关系。为了提高FRFT算法中最大的问题——如何快速确定最优阶次，快速傅里叶变换(FFT)被引入最优阶次快速估计算法。通过FFT计算信号带宽，进而初步计算出精确调频斜率的搜索范围。

对待分析信号x(t)进行FFT变换，分析其频谱的冲击束对应的频率最小值fmin与最大值fmax，即可得到带宽

B=fmin-fmax

(4)

根据该段的开始和结束时间计算出Δt，即可粗略计算调频斜率与最佳旋转角度分别为

k=B/Δt

(5)

α=arccot(-k)

(6)

该方法粗略计算得到的k值往往小于准确值，也就可以得知旋转角度的估计值大于准确值。这种估计算法计算效率极高，可以为后续搜索大大缩小范围，后续可以选取较小的步长逐步缩小α，即可得到最优旋转角度值，进而确定信号x(t)的最优变换角度。根据此角度进行FRFT变换即可得到最优变换的波形。

为说明该算法具体步骤，设置接收信号x(t)为

x(t)=exp[j(32πt2+16πt)]+n(t)

(7)

式中：调频斜率与初始频率均为32 Hz/s；信号n(t)为高斯白噪声；x(t)的信号信噪比为5 dB。取x(t)的时间区间是[-1,1](单位，s)，信号带宽设置为64 Hz，采样率为256 Hz。信号实、虚部波形与频谱结果见图1。

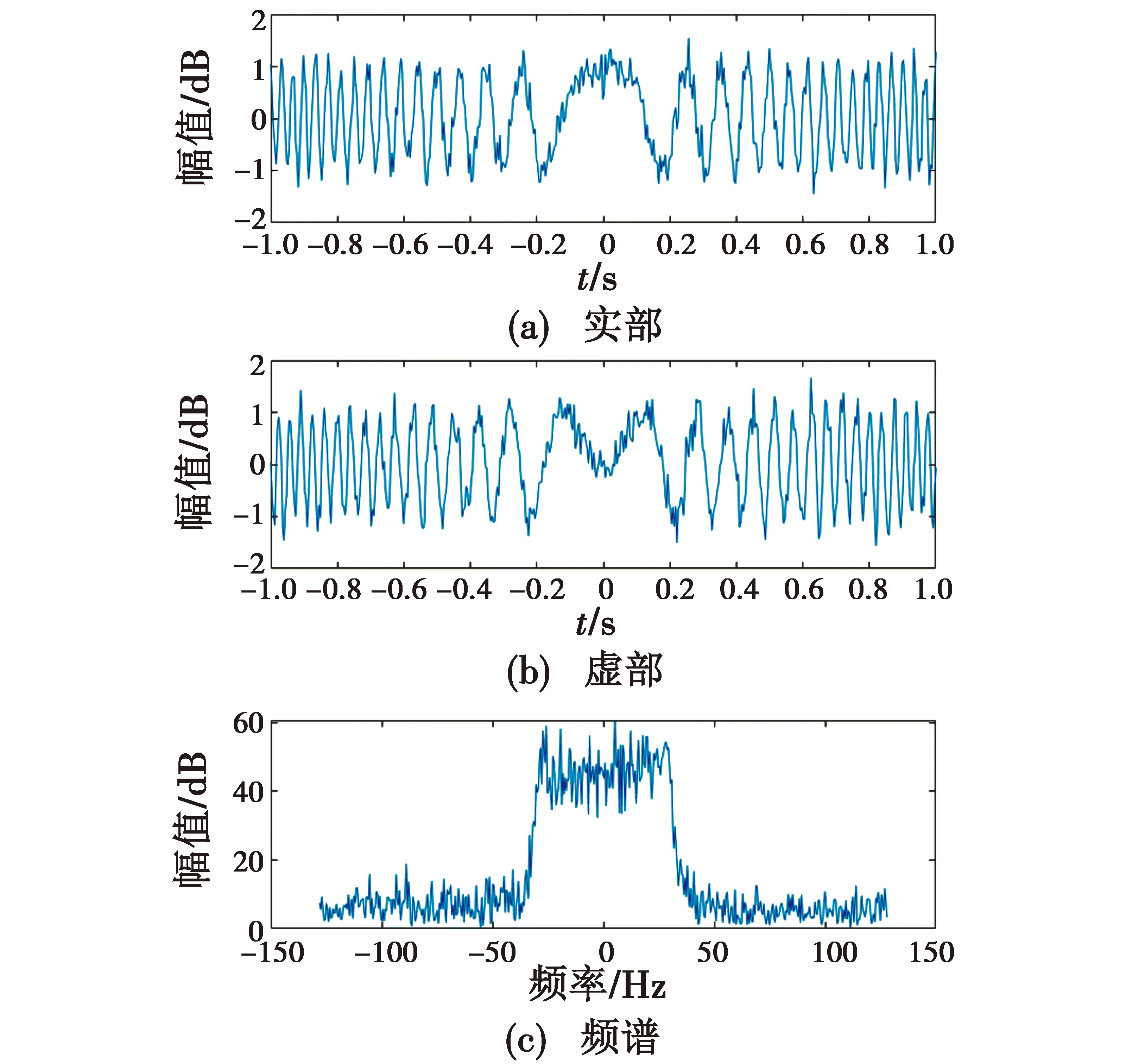
图1 Chirp信号的波形与频谱分析Fig.1 Waveform and spectrum analysis of Chirp signal

根据快速估计算法可得k≈38 Hz/s，初步估计的旋转角度是α≈106.53°，设定搜索区间为(90°，110°)，取步长0.001进行精细搜索。仿真搜索结果可得最优旋转角为104.04°，即最优阶次p=1.156。

快速算法估计调频斜率为32.009 Hz/s，估计误差仅为0.03%，因此可以说明该算法拥有较高的准确性。同时，从计算量角度来看，经典的分解法[1]确定FRFT空间峰值点坐标算法中，其计算量逼近O(NlbN)，最优旋转角度的搜索次数是m，总计算量是O(mNlbN)；而本文算法的角度搜索次数n明显小于m，总计算量是O(nNlbN)。仿真结果说明，本文算法在保证准确性的同时，大大减小了计算量，提高了算法效率。

1.3 多重分形去趋势波动分析(MFDFA)算法

MFDFA算法[8]是在去趋势波动分析算法基础上发展而来的，MFDFA算法的步骤如下所述。

1) 原始信号x(k)，k=1，2，…,N,计算信号包络

(8)

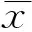
3) 利用最小二乘法拟合每一个信号子区间yi(j)(i=1,2,…,2Ns)的趋势项yi, fit(j)(j=1,2,…,s)(一阶、二阶或更高阶)，并且消除子区间的趋势项，得到序列

Zi(j)=yi(j)-yi, fit(j)。

(9)

4) 分别再求解去趋势信号子区间均方差

(10)

5) 计算各尺度q对应的波动函数

(11)

6)Fq(s)与s之间关系是Fq(s)∝sH(q)，求解广义Hurst指数H(q)

(12)

式中，广义Hurst指数H(q)是双对数坐标的线性区间的斜率值。

广义Hurst指数只是对时间序列的多重分形特性描述，而MFDFA算法中也可将H(q)转化为质量指数τ(q)、奇异函数指数γ以及多重分形谱f(γ)，换算式为

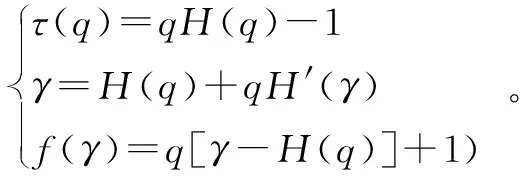
(13)

1.4 优化多重分形去趋势波动分析(IMFDFA)算法

MFDFA算法有效描述了时间序列的多重分形特性，但是存在如下两个局限。

1) 算法过程中需要进行去趋势，传统MFDFA算法使用最小二乘法拟合，多项式阶数选取会影响算法的结果，阶数的不确定性会导致信号欠拟合以及过拟合。

2) 算法分割区间的方式是等间隔分割，不连续的数据可能在相邻信号区间的分割点处出现伪波动误差，从而影响了波动函数的准确性。

本文从以下两个方面对算法进行改进。

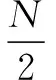
2) 已经有众多学者在传统MFDFA算法基础上进行改进，但是改进的思路仍局限于使用最小二乘法拟合去趋势项，因而，本文利用经验模式分解(EMD)算法[11]代替传统的最小二乘拟合，提取信号子区间的局部趋势项yi,emd(i=1,2,…,2Ns) ，用yi,emd代替式(7)中的yi, fit，避免了最小二乘拟合过程中多项式阶次选取不确定导致的误差。

为验证最小二乘法(以三阶为例)与EMD算法拟合信号趋势的实际效果，对同一段原始信号包络(1024点)进行拟合分析，如图2所示。

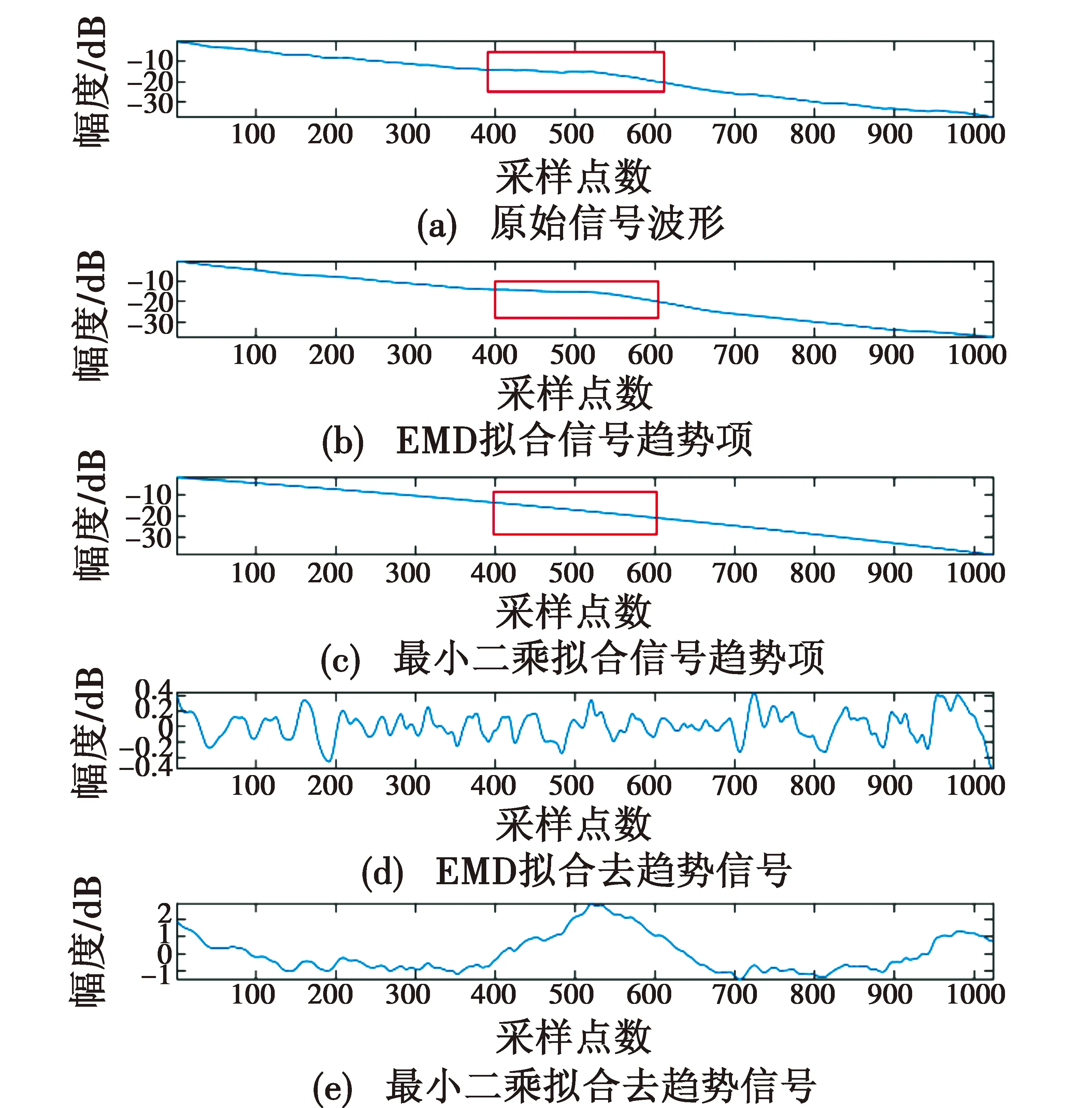
图2 最小二乘法与EMD算法拟合效果对比Fig.2 Comparison of fitting effects between least squares and EMD algorithms

由图2可看出，最小二乘法与EMD算法均可提取出信号的趋势项，但EMD算法提取趋势项在细节部分比最小二乘法提取的趋势项更好(采样点数400～600点处的信号局部特征)，对于去趋势后的信号波形，采用EMD算法得到的波动函数已经去除了明显的波形趋势，然而最小二乘法得到的波动函数因提取的趋势项在局部拟合效果不佳，导致去趋势项信号中仍有较明显的波形趋势，因而得出结论，利用EMD算法能更好地提取信号的趋势项，最终信号去趋势的效果最好。

2 变换域海杂波分形特征提取及仿真

本文的仿真数据采用1993年公布的IPIX雷达实测数据，其每个数据集均包含14个距离单元，其中，1个主目标单元，2～3个次目标单元，其余是纯海杂波单元，目标单元的信杂比在0～6 dB之间。FRFT可以使得回波信号中的目标信号能量聚集形成强冲击峰，以此来提高信号的信杂比。根据快速估计算法确定最优阶次，在最优阶次下进行FRFT变换，其频谱见图3。

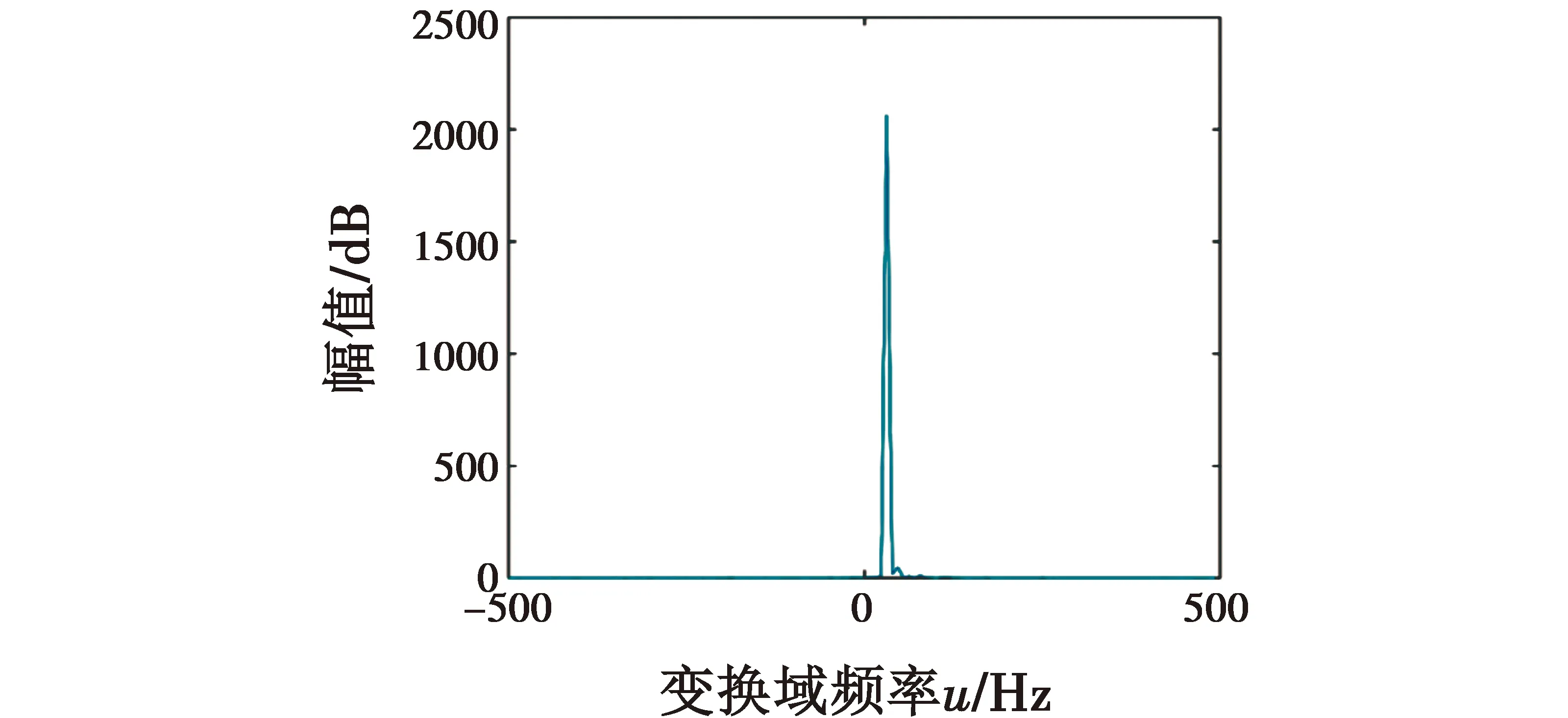
图3 目标回波的FRFT变换(最优阶次)Fig.3 FRFT transform of target echo (optimal order)

对主目标单元最优阶次下FRFT变换后，利用IMFDFA算法与MFDFA算法对其进行多重分形分析，如图4所示。

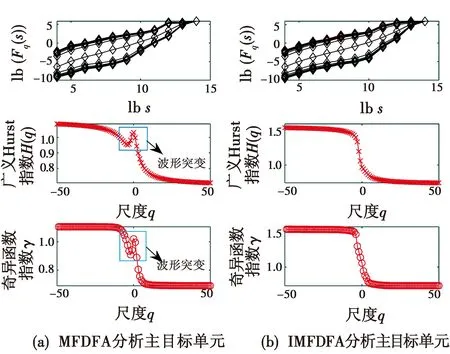
图4 主目标单元FRFT域分形分析(HH)Fig.4 Fractal analysis in FRFT domain of main target unit (HH)

由图4(b)可看出，在HH极化条件下，IMFDFA算法处理过后的波动函数与s的双对数曲线要更平滑一些，因为各尺度q(q∈ [-50,50])对应的广义Hurst指数即各波动函数无标度区间([6,11])的斜率，而传统MFDFA算法因为波动函数不平滑，在计算广义Hurst指数以及奇异函数指数曲线时，就可能出现如图4中所示的波形突变情况，影响对海杂波的FRFT域分形分析，且由图4中数据可得，IMFDFA算法的广义Hurst指数以及奇异函数指数曲线各尺度q值对应的值均略大于MFDFA分析的结果。可以得出结论：IMFDFA算法相比于MFDFA算法，波动函数与s的双对数曲线平滑了，有利于指数求解，多重分形分析效果更好，性能更稳定。

图5所示为主目标单元FRFT域分形分析(VV)。

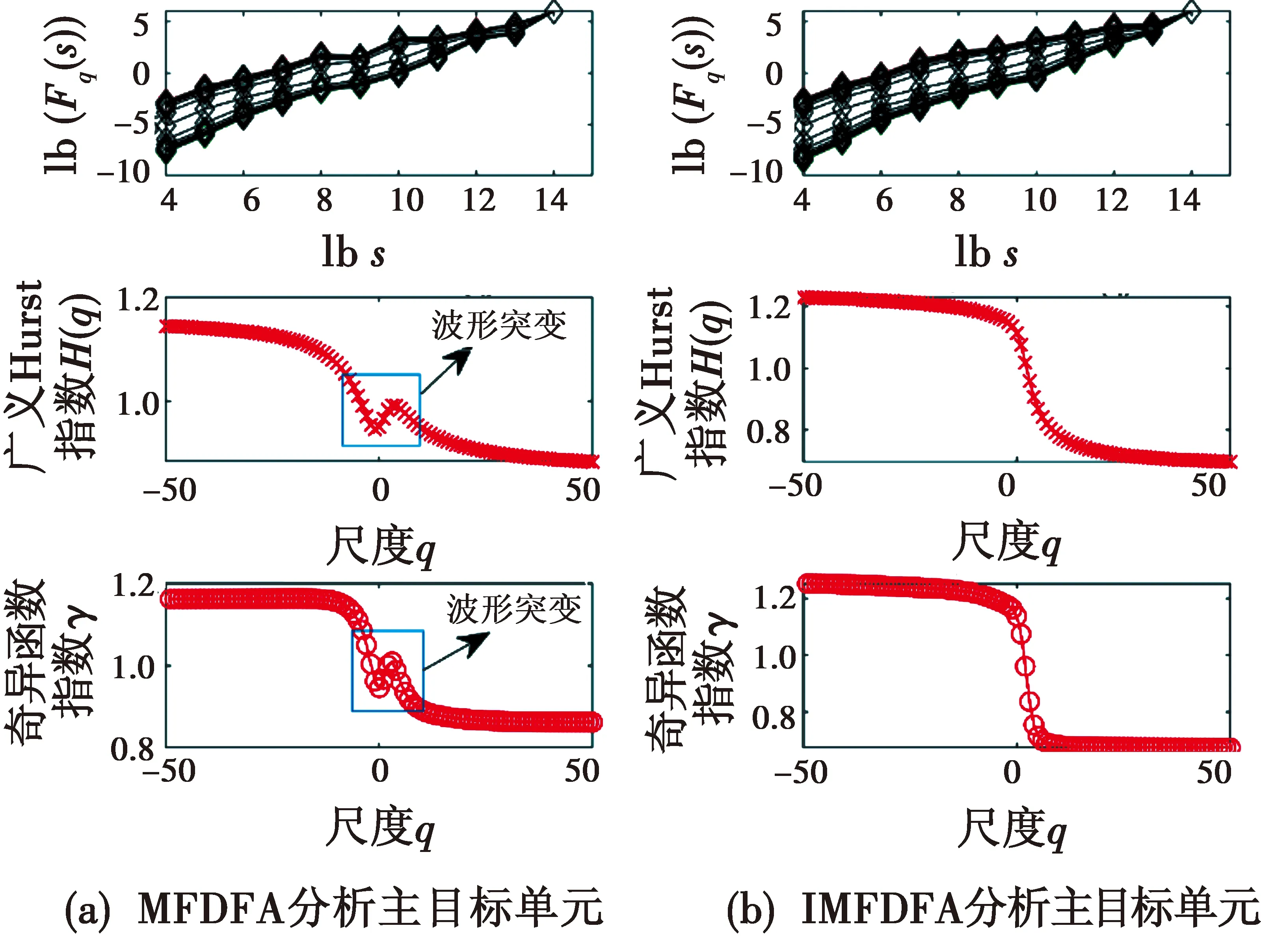
图5 主目标单元FRFT域分形分析(VV)Fig.5 Fractal analysis in FRFT domain of main target unit (VV)

对比图4与图5结果可以得出相似的结论，即在VV极化条件下，IMFDFA算法的性能优于MFDFA算法，且对比两图可得出，HH极化条件下的广义Hurst指数以及奇异函数指数均大于VV极化条件下的指数值。

为分析双极化条件(HH，VV)下采用IMFDFA算法时的海杂波FRFT域分形特性，计算#310号数据集中各距离单元在HH以及VV极化条件下的广义Hurst指数以及奇异函数指数，得到结果如图6所示。

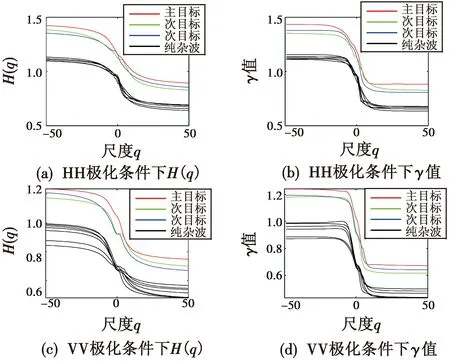
图6 HH，VV极化条件下的多重分形特性分析Fig.6 Analysis of multifractal characteristics under HH and VV

各极化条件下主目标与次目标单元的广义Hurst指数以及奇异函数指数均明显大于纯海杂波单元的值，因此可设计检测门限，选出主目标单元与纯海杂波单元差值最大的尺度定为最佳尺度，在最佳尺度下超过门限的即判定为包含目标信息，低于门限即判定为不含目标信息。

为证明FRFT域内IMFDFA算法相比MFDFA算法在目标检测性能上的优势，计算HH，VV极化条件下，IPIX雷达#310号数据集(低信杂比)中各距离单元的广义Hurst指数H(q)以及奇异函数指数γ的曲线，结果见图7。

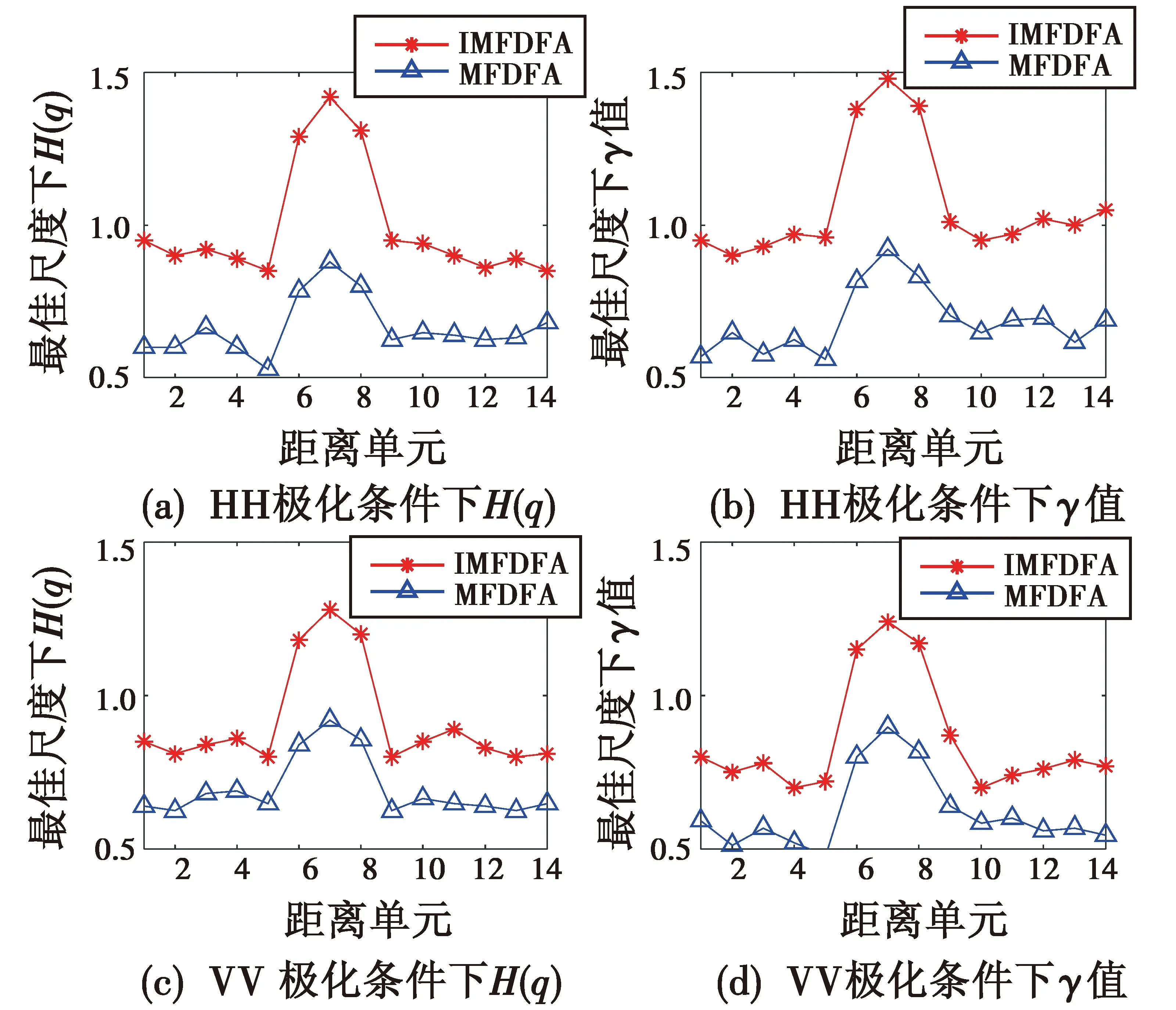
图7 IMFDFA与MFDFA算法结果分析Fig.7 Analysis of IMFDFA and MFDFA algorithm results

最佳尺度下进行多重分形，IMFDFA算法的主、次目标单元的Hurst指数与奇异函数指数均明显大于纯海杂波单元，且相比于MFDFA算法结果，IMFDFA算法形成的峰值更陡峭，更有利于检测器的设计。

3 结束语

本文就海杂波中小目标检测难点问题，针对现有的FRFT域分形检测算法进行改进，提出了基于变换域分形的海面小目标快速检测算法，利用FRFT与最优阶次快速估计算法实现了海杂波最优阶次下的快速变换，并且针对传统MFDFA算法的不足，提出了IMFDFA算法，改善了MFDFA算法的多重分析能力，提高了算法的稳定性，最后分析了FRFT域下多重分形特征，利用主目标单元与纯海杂波单元的广义Hurst指数以及奇异函数指数间的明显差异，可设定检测门限，检测雷达回波中是否包含目标信息，使新算法提高了实际应用的可能性。