四电机独立驱动FSEC赛车行驶状态估计

武亚南，李 刚，宋成镖

四电机独立驱动FSEC赛车行驶状态估计

武亚南，李 刚，宋成镖

（辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121001）

针对赛车行驶状态过程中的估计问题，提出了一种基于容积卡尔曼滤波的车辆行驶状态估计算法。以四电机独立驱动FSEC赛车为研究对象，选取三自由度车辆动力学模型作为估算模型，设计基于轮胎数据的侧向力查表模块，结合纵、侧向加速度、横摆角速度以及驱动力矩、前轮转角等共同作为估算算法的输入参数，得到状态预测值与误差协方差矩阵。经过卡尔曼增益的测量校正，最终可得到纵、侧向速度估计值与横摆以及加速度校正值，从而实现对车辆行驶状态的准确估计。选择典型的实验工况，应用Matlab/Simulink搭建算法模型并与CarSim联合仿真对算法进行验证。结果表明：基于容积卡尔曼滤波的汽车估计算法能够较准确地、稳定地对车辆行驶状态进行估计，并降低了车辆行驶状态采集的成本。

四电机独立驱动；状态估计；容积卡尔曼滤波；信息融合；仿真验证

汽车关键状态与参数变量的准确获取是进行车辆主动安全控制以及稳定性控制的前提。车辆状态参数一般是通过安装在车辆上的传感器直接获取的，由于四电机独立驱动FSEC赛车特殊的动力系统布置形式，使一些状态信息无法采用此方法获得。通过实验室用特殊实验仪器可获取相关信息，但这种仪器价格昂贵，需要特殊的安装方式，同样也不适用于空间紧凑的赛车。

关于四电机独立驱动FSEC赛车的状态参数估计，国外已有研究。挪威科技大学的大学生方程式团队[1]开发出一款整车控制器，该控制器将采集的惯性原件与GPS信息，通过嵌入Kalman滤波算法融合数据从而获得准确的速度信息。里斯本大学的大学生方程式团队[2]开发了侧偏角估计算法，该算法建立了三级滤波结构，首先是车辆姿态滤波器，通过融合来自磁场强度计与陀螺仪的横摆角信号矫正车辆姿态信息；第二部分是带有自校准功能的位置互补滤波器，通过融合GPS位置信息与加速度信息估算出速度分量，最后通过对比线性与非线性动力学模型的结果得出所需估计量。Bartolke等[3]为四轮驱动电动方程赛车电控系统匹配了控制算法，其利用直接安装在车辆上的惯性导航（INS）传感器，结合Kalman滤波算法开发车速估计器，并设计了稳定性控制算法。

四电机独立驱动的动力布置形式刚刚引入国内，针对FSEC赛车车速估计的研究较少，可以参考现有的车速估计方法，如最小轮速法、轮速集中法、斜率法、加速度积分法等[4-6]。

此外也有针对四电机独立驱动平台车辆行驶状态参数估计的研究，王野[7]提出一种基于容积卡尔曼滤波框架的车辆行驶状态参数、路面附着系数、车辆参数联合估计算法。张家旭等[8]提出一种交互式模型的自动驾驶车辆速度无迹卡尔曼滤波估计方法，该算法基于自动驾驶车辆的定位信息建立了包含运动学、动力学特性的车辆模型，并采用无迹卡尔曼滤波器对速度进行实时估计，通过交互式多模型算法平滑滤波器输出，由此实现对系统噪声统计特性的自适应能力。

在行驶状态估计方面，国内外学者都做了大量研究。国外大多采用线性卡尔曼滤波加惯性元件的双级校正估计方案，该方法有效规避车辆模型线性化的精度问题，但增加了惯性元件等设备，使得赛车的制造成本增加。国内则大多采用非线性卡尔曼滤波，构成状态估计与路面附着多级自校正估算架构，有效解决了滤波算法输入参数不确定的问题，但该算法计算量庞大且对硬件要求高。本文选择容积卡尔曼滤波，从单项式准确积分视角求解非线性系统方程简化计算，并选取三自由度车辆模型直接推算变量关系，从而使估计算法有较高的效率和实时性。

1 车辆估算模型

1.1 三自由度车辆动力学模型

估算模型采用三自由车辆动力学模型，由其抽象出的动力学公式表征不同参数在车辆运动过程中的物理关联。本文研究的对象是四电机独立驱动FSEC赛车，考虑到整个算法的结构与输入输出条件，选取三自由度车辆动力学模型作为状态估计的参考模型，并做以下假设：①参考坐标系原点与赛车质心重合；②赛车没有侧倾和俯仰方向的自由度；③忽略悬架弹跳行程的影响。将模型简化为由一个刚性车体连接四个相互独立控制的车轮构成，如图1所示。

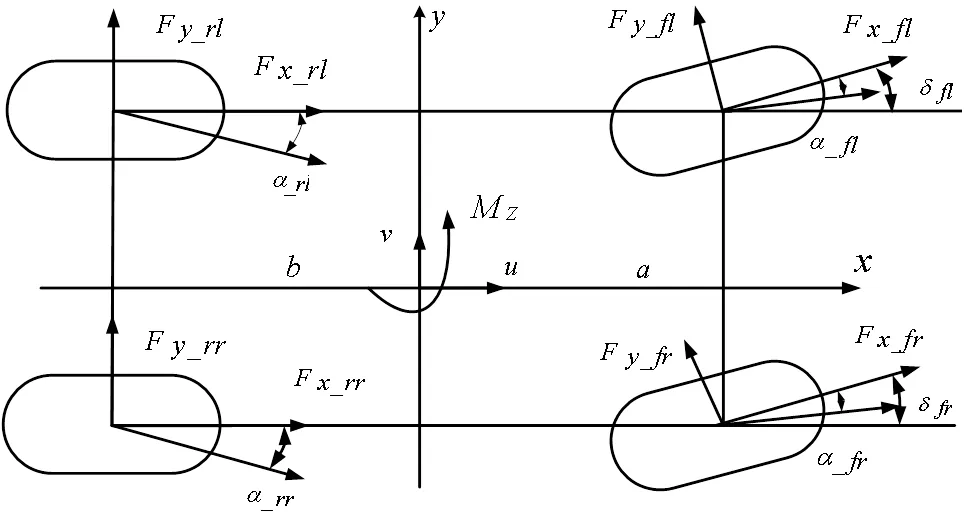
图1 三自由度车辆估算模型

模型是基于单轨车辆模型，增加纵向自由度而建立的，其动力学方程式如(1)～(3)所示。

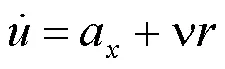
式(1)～(3)中：a为纵向加速度，a为侧向加速度，为纵向车速，为侧向车速，为横摆角速度，I为绕轴的转动惯量，M为横摆力矩。

由于车辆运动是外力作用的结果，上式中的加速度与力矩也可由作用在轮胎上的力间接得到。在以往的一些研究中，通常将轮胎模型简化为线性模型，最终可将动力学方程简化为与状态变量呈线性关系的方程。本文将直接采用轮胎力的方式对加速度与力矩进行推导，相比于线性模型更加的精确。其中纵、侧向加速度以及横摆力矩计算公式如下：

式(4)、(5)中：F_ij为四轮纵向力，F_ij为四轮侧向力，δ为四轮转角，为车辆总质量。

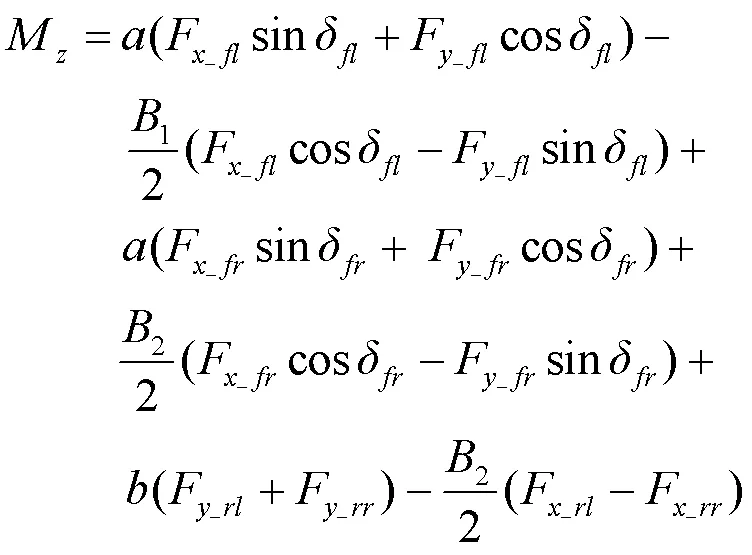
式中：、分别为质心到前后轴的距离，1、2分别为前后轮的轮距。

1.2 轮胎模型

地面是赛车与外界的接触渠道之一，而轮胎是与地面接触的系统。地面作用力是通过轮胎传递到质心上，尽管这些力受方向盘转角、车辆载荷转移等因素影响，但其最终均由轮胎特性决定，所以轮胎模型的设计对论文研究内容有很重要的意义。

文中所研究的赛车在轮胎设计时选择的是马牌C19轮胎，该轮胎是马牌轮胎专门为大学生方程式赛车研发的一款小载荷高性能轮胎，其提供了轮胎实验数据与参考拟合公式，并根据实验工况不同设计了不同的轮胎参数文件，可直接加载到CarSim等动力学仿真软件中进行相应的轮胎实验。考虑到仿真的时效性问题，在Matlab/Simulink中搭建轮胎模型时采用查表的方式，采集CarSim轮胎实验输出的曲线数据。

轮胎模型的建立一般采用轮胎台架数据结合经验公式的方法建立轮胎数学模型。最常用的是“魔术公式”轮胎模型，可由式(7)表示。

魔术公式的好处在于通过一组公式表征了轮胎在3个方向的分力，如式(7)中，Y为输出变量，可由纵向力Fx、侧向力Fy或回正力矩Mz来表示；x为输入变量，可由轮胎的侧偏角α或纵向滑移率k表示；B、C、D、E分别为刚度因子、形状因子、峰值因子和曲率因子，公式模型如图2所示。

本文研究的车速估计算法只考虑轮胎纵向力与侧向力，不考虑回正力矩，如式(8)、(9)所示。

根据拟合数据最终经过查表可以得到不同垂直载荷下，侧向力与侧偏角、纵向力与滑移率之间的关系曲线，如图3所示。

图3 赛车轮胎模型

2 车辆行驶状态估计算法设计

2.1 估计算法架构

四电机独立驱动FSEC方程式赛车行驶状态估计算法架构如图4所示，该算法架构主要分为3个部分，首先是利用赛车仿真模型或实车传感器采集的信号；其次配合相应物理模型对所需的中间变量进行推断处理、运用轮胎查表模块计算轮胎侧向力；最后通过容积卡尔曼滤波算法框架估算行驶状态参数值。

首先通过采集到的传感器信号，包括纵、侧向加速度、横摆角速度以及作用在4个车轮上的驱动力矩，结合方向盘转角等信号，利用加速度信号解算出作用在每个车轮上的垂向力。另外根据方向盘转角与估算出的纵向速度、侧向速度等可计算每个轮胎的侧偏角，进而根据轮胎查表模型求解出作用在每个车轮上的轮胎侧向力，而轮胎纵向力则可以通过电机输出驱动力矩信号直接换算得到。轮胎纵向力、侧向力及方向盘转角信号汇总后进入滤波模块，作为系统方程的输入对行驶状态参数进行预测，其余信号可作为观测量对预测结果进行修正。

图4 行驶状态估计原理图

2.2 估计算法建立

本文基于容积卡尔曼理论[9-11]建立车辆行驶状态估计算法。容积卡尔曼滤波是加拿大学者在2009年提出的一种新型非线性高斯滤波方法[12-13]，经严格数学证明其逼近非线性变换后的概率分布精度优于UKF[14]。由于计算舍入等误差容易导致CKF算法误差协方差矩阵失去正定性，而基于奇异值分解（SVD）代替Cholesky分解可以解决误差协方差平方根矩阵的非正定性问题[15-16]。

设计状态估计器要建立系统的状态向量和测量向量，按照算法架构需求与选用的动力学模型抽象的非线性系统方程，确定系统的输入向量如式(10)所示。

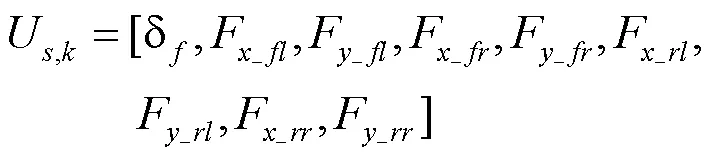
式中：δ代表前轮转角，F_ij、F_ij分别代表4个车轮的纵向力和侧向力。

由于可用传感器信号以及状态信息更新的需求，结合车辆动力学模型的输出结果，可确定系统状态向量如式(11)所示。

式中：ν、ν分别为车辆的纵向速度与侧向速度，纵向速度是进行车辆动力学控制的一个重要参数，二者比值为质心侧偏角，可用于轮胎模型的输入；aa分别为由传感器得到的纵、侧向加速度以及横摆角速度。

观测变量的设置是状态变量的一部分，通过观测变量对状态变量进行更正，保证状态估计结果的可靠性，系统观测向量如式(12)所示。

（1）时间更新

利用SVD法将上个时间点的误差协方差矩阵P-1进行分解，如式(13)所示。

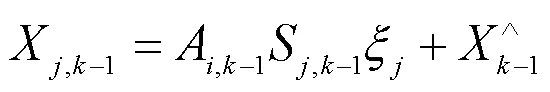
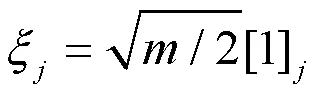
本文中车辆行驶状态变量的阶数=6，则容积点集如式(15)所示。

计算经过系统方程更新后的容积点，如式(16)所示。

“有吃的还堵不住你的嘴呀？”陆浩宇说。他没有问是谁送的早餐，难道他猜到是我放的？还是他根本不在乎是谁？心里有些失落，一连五天，我每天变着花样给陆浩宇带早餐，而他一次也没吃，还把我特意为他准备的早餐都送给了没吃早饭的同学。

对容积点状态值求平均，预测经时间更新后的状态值，如式(17)所示。

对误差协方差求解时间更新预测值，如式(18)所示。

式中：为过程噪声的协方差矩阵。

（2）测量更新

使用SVD法将时间更新后的P/k-1分解，如式(19)所示。

计算当前时刻容积点，如式(20)所示。

根据测量方程更新容积点，如式(21)所示。

对容积点求均值，如式(22)所示。

计算新息方差，如式(23)所示。

式中：为测量噪声协方差矩阵。

计算互协方差，如式(24)所示。

计算卡尔曼滤波增益，如式(25)所示。

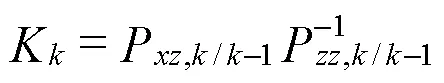
测量变量校正后的状态估计，如式(26)所示。

校正误差协方差矩阵，如式(27)所示。

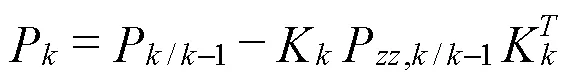
3 仿真验证

仿真验证是对状态估计算法性能的检验，查看其是否能够准确估计车辆行驶状态参数。为验证所提出估计算法的可行性和可靠性，在Matlab/Simulink环境下搭建相应的算法模型，同时与CarSim进行联合仿真，评估估计算法对车辆非线性行驶状态的估计效果。在仿真工况的选取上也尽可能贴近赛道路况的设计，简化出典型的测试道路条件与附加条件。

状态估计器初始值如下：

X1,0=[0，0，0，0，0，0]，

P1,0=(6)×100，

Q1,0=(6)，

R1,0=([0.01，1，0.08])×0.01。

赛车模型部分参数如表1所示。

表1 赛车部分基本参数

参数名称数值参数名称数值 车重/kg265轴距/mm1550 质心至前轴距/mm852.5质心高度/mm205 总宽/mm1475总高/mm1140 前轮距/mm1220后轮距/mm1200 簧载质量/kg165前后载荷比45:55 迎风面积/m20.23左右载荷比1:1 转向节臂长/mm75.4轮胎半径/mm235 前后轮胎宽比1转向传动比5:1 主销内倾角/(°)3主销后倾角/(°)3 前轮外倾角/(°)-3前轮前束角/(°)-3

（1）稳态圆周工况

稳态圆周工况是比赛第二个项目八字绕环的基本组成单元，具体工况设置如下：30 m半径封闭圆周道路，路面附着系数为0.85，转向为驾驶员闭环控制，静止启动单电机2.5 N·m恒转矩输出。

车辆行驶状态仿真如图5所示。

图5中的(a)、(b)是估计算法得到的状态信息与CarSim输出的相应真实值之间的对比曲线图。(a)为纵向车速对比曲线，从图中可看出估计结果在仿真开始时能较好跟踪模型输出值，且随仿真时间增长，误差没有累计，而是围绕真实值小幅进行波动。(b)为侧向车速对比曲线，从图中可看出在仿真进行到3 s时，出现严重不重合现象，原因可能是因为纵向加速度在3 s时出现严重波动，导致侧向加速度误差累计。但随着时间的增加，侧向速度逐渐向真实值靠近，总体来看侧向速度能够围绕在真实值附近，误差在可接受范围内。(c)、(d)、(e)为纵、侧向加速度与横摆角速度的测量量，由于在仿真过程中没有加入噪声干扰，所以估计值与真实值是一致的。

（2）高速双移线工况

高速双移线工况是赛车在比赛中经常遇到的典型工况，比如赛道超车区，考验赛车在较高速度突然进行大幅度横向转移的稳定性。

具体工况设置如下：路面附着系数为0.85，转向采用闭环驾驶员预瞄模型，静止启动，每个电机10 N·m输出。车辆行驶状态仿真如图6所示。

图6中的(a)、(b)是估计算法获取的赛车状态信息与CarSim软件输出的相应真实值之间的对比曲线图。(a)为纵向车速对比曲线，从图中可看出估计结果在仿真开始时能够较好的跟踪模型输出车速值，但仍存在一定的误差，且随着仿真时间的增加，误差逐渐累计。但车速估计值还是与真实值有很大一部分重合的，且在整个仿真域来看差值并不是十分明显，在可接受范围之内。(b)为侧向车速对比曲线，从图中可以看出在仿真进行到转向时开始出现不重合的现象，并且在曲线峰值附近有一定幅度的超调，但是总体来看在恢复到直线行驶阶段之后侧向速度能够围绕在真实值附近，综合分析估计效果明显，误差在可接受范围内。(c)、(d)、(e)为纵、侧向加速度与横摆角速度的测量量，由于在仿真过程中没有加入噪声，所以估计值与真实值是一致的。

（3）双移线工况硬件在环实验

行驶状态参数估计的硬件在环实验选取加速双移线工况，驾驶模拟器硬件在环实验主要是验证行驶状态估计算法在硬件在环实验台上的运行效果。具体工况设置如下，双移线路径，路面附着系数为0.85，转向采用驾驶员输入，静止启动，油门由驾驶员控制。车辆行驶状态仿真如图7所示。

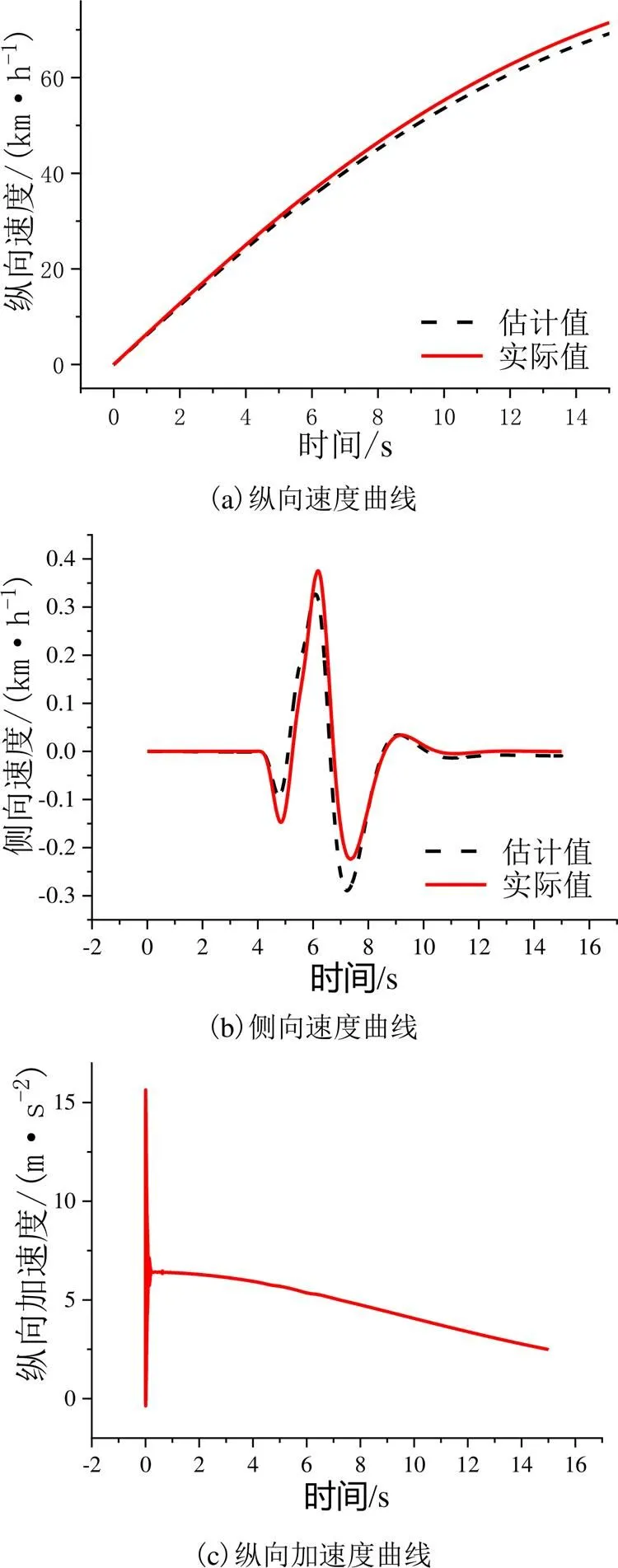
图7中的(a)、(b)是估计算法在硬件在环实验台上获取的赛车状态信息与由CarSim RT软件输出的相应真实值之间的对比结果。(a)为纵向车速对比曲线，从图中曲线可以看出估计结果始终能够较好跟踪真实值，与软件仿真实验结果类似，估计算法在硬件在环实验台上可以稳定工作。(b)为侧向车速对比曲线，从图中可以看到在仿真进行到转向开始的时刻出现曲线略微不重合现象，并且在曲线峰值附近有一定幅度的超调，但是估计准确程度甚至超过了软件在环仿真实验，这是由于对原始数据过滤处理的结果，综合分析估计效果明显。(c)、(d)、(e)为纵、侧向加速度与横摆角速度的测量量，由于在仿真过程中并没有加入噪声干扰，只有自身噪声，过滤后数据趋势明显，但是可看出数据并不像软件仿真数据那样平滑，数据真实有效。

4 结语

（1）本文对赛车行驶状态估计算法进行研究。利用容积卡尔曼滤波理论，构建估计算法框架，选取三自由度车辆动力学模型作为估算模型，设计基于轮胎数据的侧向力查表模块，结合纵、侧向加速度、横摆角速度、以及驱动力矩、前轮转角等共同作为估算算法输入参数，得到状态预测值与误差协方差矩阵，经过卡尔曼增益的测量校正，最终可得到纵、侧向速度估计值与横摆以及加速度校正值。

（2）运用Matlab/Simulink对其进行模块化编程实现，同时搭建车辆仿真模型联合CarSim仿真平台对估计算法进行验证，仿真结果表明：该算法对行驶状态的估计在响应性、稳定性和准确性方面具有良好的效果。

（3）行驶状态估计算法由于数据量庞大，对车辆硬件条件提出较高要求，算法很难实现在线实时运行，在后续可以进一步研究。

[1] Bolstad L H, Fj Sne A, Haukali M, et al. Electronic systems for a formula student racing car[J]. Atzextra Worldwise, 2017, 22(S2): 50-53.

[2] Andre A, Cardeira C, Oliveira P. Application of Sideslip Estimation Architecture to a Formula Student Prototype[J]. Robotics and Autonomous Systems, 2017(115): 83-89.

[3] Bartolke A, Michael T, Scheider J. Die Eeue Formula Student Electric[J]. Formula Student Electric Technology Highlights, 2017(9): 62-69.

[4] 吴利军, 王丽芳. 一种基于加速度及轮速信号的参考车速估计方法[J]. 汽车技术, 2011(1): 45-48.

[5] QI Zhi-Quan, MA Yue-Feng, ZD Liu, et al. Estimation of Vehicle Speed Based on Wheel Speeds from ASR System in Four-Wheel Drive Vehicles[J]. Journal of Beijing Institute of Technology, 2010, 19(2): 153-157.

[6] Chen T, Xing X, Long C, et al. Estimation of longitudinal force, lateral vehicle speed and yaw rate for four-wheel independent driven electric vehicles[J]. Mechanical systems and signal processing, 2018, 101(FEB.15): 377-388.

[7] 王野. 四轮独立驱动与转向电动汽车状态与参数估计[D]. 锦州: 辽宁工业大学, 2018.

[8] 张家旭, 王晨, 王欣志, 等. 基于自适应滤波器的无人驾驶汽车速度估计[J]. 华南理工大学学报: 自然科学版, 2021, 49(1): 74-81, 9.

[9] 霍光. 基于容积卡尔曼滤波的单站无源定位跟踪算法研究[D]. 郑州: 郑州信息工程大学, 2013.

[10] 徐树生, 林孝工. 基于鲁棒CKF的多传感器全信息融合算法[J]. 电机与控制学报, 2013, 17(2): 91-97.

[11] 鹿传国, 冯新喜, 张迪. 基于改进容积卡尔曼滤波的纯方位目标跟踪[J]. 系统工程与电子技术, 2012, 34(1): 28-33.

[12] Arasaratnam I, Haykin S, Hurd T R. Cubature Kalman filters[J]. IEEE Trans on Automatic Control, 2009, 54(6): 1254-1269.

[13] Arasaratnam I, Haykin S, Hurd T R. Cubature Kalman filtering for continuous-discrete systems theory and simulations[J]. IEEE Trans on Signal Processing, 2010, 58(10): 4977-4993.

[14] 魏喜庆, 宋申民. 无模型容积卡尔曼滤波及其应用[J].控制与决策, 2013, 28(5): 770-773.

[15] 石章松, 王树宗, 刘忠. 基于SVD的机动目标自适应滤波研究与仿真[J]. 海军工程大学学报, 2013, 15(2): 54-56.

[16] 张秋昭, 张书毕, 郑南山. GPS/INS组合系统的多重渐消鲁棒容积卡尔曼滤波[J]. 中国矿业大学学报, 2014, 43(1): 163-168.

Research on Driving State Estimation of FSEC Racing Cars Driven Independently by Four Motors

WU Ya-nan, LI Gang, SONG Cheng-biao

（School of Automobile and Traffic Engineering, Liaoning University of Technology, Jinzhou 121001, China）

In order to estimate the driving state of the racing car, a vehicle driving state estimation algorithm based on the cubature Kalman filter is proposed. The FSEC racing car driven independently by four motors is taken as the research object and the three-degree-of-freedom vehicle dynamics model is selected as the estimation model. A side force look-up table module based on tire data is design, longitudinal and lateral acceleration, yaw rate, driving torque, front wheel angle, etc. combined as the input parameters of the estimation algorithm to obtain the state prediction value and the error covariance matrix. After the Kalman gains correction, the estimated value of the longitudinal and lateral speed and the correction value of the yaw and acceleration can be finally obtained, so as to achieve an accurate estimation of the vehicle driving state.Typical experimental conditions are selected and Matlab/Simulink is used to build an algorithm model and co-simulate with CarSim for verification. The experimental results show that the estimation algorithm based on the cubature Kalman filter can estimate the vehicle driving state more accurately and stably, and reduce the cost of collecting the driving state of the vehicle.

four motors driven independently; state estimation; cubature Kalman filter; information fusion; simulation verification

10.15916/j.issn1674-3261.2022.04.001

U461.9

A

1674-3261(2022)04-0211-07

2021-08-16

辽宁省自然科学基金面上项目(2022-MS-376)

武亚南(1996-)，女，山西太原人，硕士生。

李 刚(1979-)，男，辽宁朝阳人，教授，博士。

责任编辑：陈 明