曲面边缘均匀喷涂的路径分片规划方法

苏成志，刘军，李华，王虹霖，王恩国

(1.长春理工大学人工智能学院，吉林长春 130022；2.长春理工大学重庆研究院，重庆 401135；3.哈尔滨飞机工业集团有限责任公司，黑龙江哈尔滨 150000)

0 前言

喷涂机器人是工业机器人在涂装领域的一种应用，它是机器人技术与喷涂工艺相结合的产物。喷涂机器人作为智能化喷涂设备，已被广泛运用在诸如汽车、飞机等具有复杂曲面的工业产品的涂装作业中。使用机器人喷涂时，喷涂机器人末端安装的自动喷枪需要在工件表面以恒定的喷涂距离和喷涂速度移动，使工件表面喷涂均匀。因此，喷涂的质量和效率主要取决于喷涂路径的合理性。近年来，随着喷涂机器人日益广泛应用，喷涂机器人的路径规划技术从早期的手工教学发展到基于三维模型的离线编程，用于自动生成喷涂路径，因此喷涂路径规划算法得到了广泛的研究和快速的发展。

SHENG、CHEN等在生成Bounding Box的基础上，将一组平面与表面三角形网格的交线转化生成喷涂路径。ATKAR等提出了一种在表面生成种子曲线的方法，选择种子曲线上的一组偏移曲线作为喷涂路径。ANDULKAR、 CHIDDARWAR提出一种增量式轨迹生成方法，该方法中新的喷涂路径由之前喷涂路径在表面的涂层累积厚度所决定。ZHANG等提出了一种考虑曲面边界的偏移喷涂路径规划方法，根据喷涂高度的允许范围和涂层厚度的误差范围，建立了相邻路径的间距变化范围；在此基础上，采用平面截距线等分法，生成曲面长度方向上喷涂路径的离散点，以此生成曲面的喷涂路径。

上述方法都是基于曲面三角网格模型所提出的喷涂路径规划方法。然而在实际生产中，很多待喷涂工件的三角网格模型只能借助逆向工程由点云模型转换而来，但是在转换过程易出现孔洞、自相交等瑕疵，不利于实现机器人喷涂路径自动规划。由于点云模型可以描述任何复杂形状，并且可以很容易地从CAD模型或测量设备中获得，因此具有实用性，故针对点云模型研究喷涂路径规划具有更加重要的实际意义。近年来，一种被称为点云切片的算法值得关注，该方法最早应用于逆向工程领域用于快速模型重建，也被用于数控机床刀具轨迹的生成，其最大的优点是可以直接从点云模型生成路径，无需任何预处理工作。孙国朋、吴炎凡与TONG等基于点云切片技术实现了基于曲面点云模型的机器人喷涂路径规划，但是其所得栅格路径在曲面边缘处喷涂不均匀。

现有的基于点云模型的喷涂路径自动生成工作大都是借助切片法实现。切片法虽能针对点云模型自动生成喷涂路径，但缺点在于其核心是用一系列等距的平面族与待喷涂曲面相交，即只有切平面与曲面相交的地方能产生喷涂路径，易造成曲面边界处生成的喷涂路径比实际所需的路径短。另外曲面的几何尺寸往往不能被等距的平面族整分，这都会导致生成的喷涂路径在曲面边缘处喷涂不均匀。

针对现有研究工作中存在的曲面边缘喷涂不均匀问题，提出了一种曲面边缘均匀喷涂的路径分片规划方法。该方法首先构建曲面外扩包围盒；基于外扩包围盒将曲面分片成每条喷涂路径所对应的单条曲面；然后将单条曲面分片成单个路径点所对应的单片曲面；对于每一个单片曲面，生成一个喷涂路径点；最后对每条喷涂路径进行过喷处理，最终形成喷涂路径。针对具有规则边缘的车门主表面以及具有不规则边缘的翼子板分别进行了喷涂路径规划与涂层累积厚度仿真，并与切片法进行比较，对该方法进行验证。

1 喷涂路径分片规划方法

分片规划方法不同于切片法用一系列等距的平面族与待喷涂曲面相交求取喷涂路径的思路，而是利用主、副切片将曲面分片为单个喷涂路径点对应的单片曲面，避免曲面边缘处没有喷涂路径点与之对应，保证了曲面边缘的喷涂涂层均匀性。假设喷涂路径是在已知曲面点云模型、喷枪涂层分布模型、相邻路径点间距以及喷涂参数等输入参数的结构化环境中生成的，其中喷涂参数包括喷枪偏移距离、喷涂速度以及相邻喷涂路径间距。

1.1 构建曲面外扩包围盒

如图1所示，在生成曲面喷涂路径时，路径方向应沿着曲面的最长边界方向，此时路径折返次数最少；喷枪指向应垂直于工件表面。基于此，借助主成分分析(PCA)法构建有向包围盒(OBB)，以此来自动确定喷枪初始指向、路径初始方向、主切片平面法方向。

图1 喷涂路径示意

首先，曲面数据集{}的协方差矩阵由式(1)确定：

(1)

进而对协方差矩阵进行特征值分解，可以分解为3个特征向量、和，3个特征向量对应的特征值分别是，和，其中≥≥。

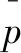
(2)

此时曲面数据集{}:

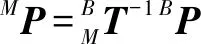
(3)

易得曲面点云数据集{}在、以及方向的最大值和最小值分别为、、、、、。

此时曲面有向包围盒(OBB)为

(4)

式(4)中:′为曲面包围盒在坐标系{}的一个顶点，′、′，′分别为包围盒上与′共边的另外3个顶点。

最后由式(5)可将曲面有向包围盒转换到基座标系{}:

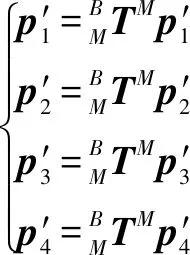
(5)

此时，喷枪初始方向、路径初始方向、主切片平面法方向分别为

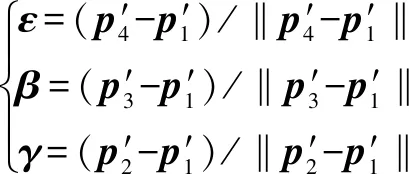
(6)

设喷枪在偏移距离时的涂层区域半径为，设相邻路径最优间距为。

由第1.2小节可知，相邻主切片间距为/2。如图2所示，第一条路径与其相邻边界最大距离应小于等于,当其距离等于时，其涂层均匀性最好且使第一条路径油漆浪费量达到最小。

图2 相邻路径的涂层影响区域原理

故有向包围盒应沿主切片平面法向外扩Δ：

Δ=-2

(7)

如图3所示，此时曲面外扩包围盒为

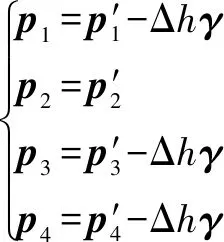
(8)

式(8)中:Δ为包围盒外扩高度。

1.2 基于外扩包围盒分片生成单条曲面

曲面栅格喷涂路径如图1所示，其相邻路径的涂层厚度累积截面曲线如图2所示。以第2条路径为例，其喷涂区域宽度为2。在宽度为2的喷涂区域中，宽度为2的喷涂区域涂层累积情况完全由第二条路径本身所决定，宽度为Δ的喷涂区域涂层累积虽然由相邻两条喷涂路径共同决定，但是其主要由第2条喷涂路径决定，故单条喷涂路径所影响的单条曲面区域宽度可近似为。如图3所示，为了将曲面分片为单条路径所对应的单条曲面，借助一系列主切片平面将曲面分片为宽度为2的小曲面，此时相邻两个小曲面则构成单条曲面。

图3 曲面外扩包围盒及主切片示意

首先，主切片平面个数为

(9)

式(9)中：ceil是向上取整函数；与为曲面外扩包围盒在主切片平面法方向的两个顶点。

主切片平面上一确定点为

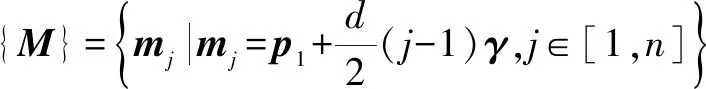
(10)

式(10)中:为第个主切片平面上一确定点。 故主切片平面集{}为

{}={|·(-)=0,∈[1,]}

(11)

式(11)中:为第个主切片平面;=(,,)为上任一点;为主切片平面个数。

此时，曲面点集{}中第个点在主切片平面{}间的位置为

=,·≥0且·+1<0

(12)

式(12)中:=表示点在主切片平面与+1之间。

最后，将曲面点集{}代入式(13)即可实现曲面分块：

{}={|={,=2-1||=2},

(13)

式(13)中:表示第条路径所对应的单条曲面点集;表示曲面点集{}中第个点;floor为向下取整函数。

1.3 基于单条曲面分片生成单片曲面

单条喷涂路径由一系列离散路径点构成，设相邻路径点间距为。虽然喷涂是一个连续的过程，但此时可以将单条曲面涂层累积看做仅由这一系列离散路径点所决定，即将单条曲面分片为每个路径点所对应的单片曲面。如图4所示，为了实现单条曲面分片，借助一系列副切片平面将单条曲面进行分片。

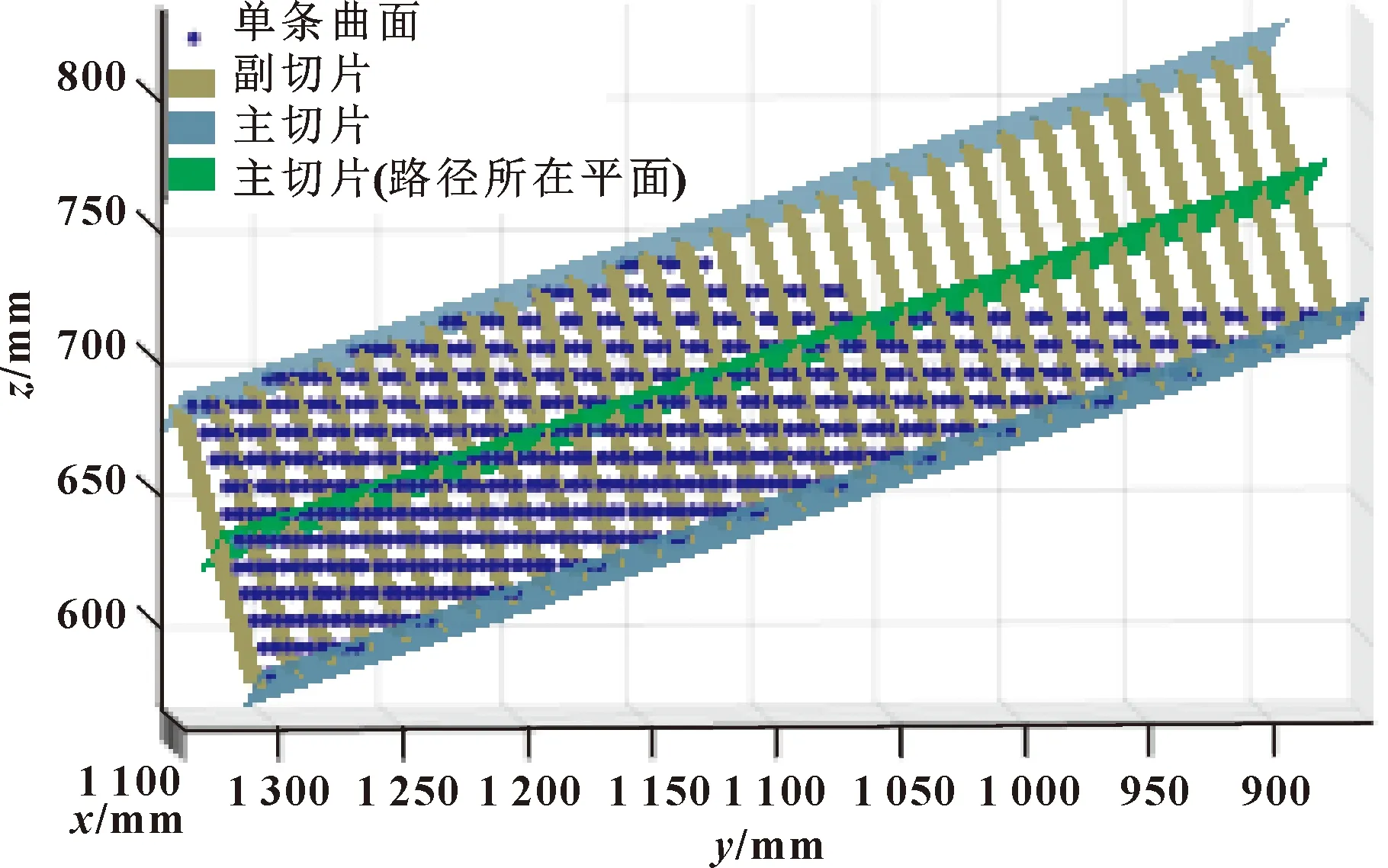
图4 单条曲面及其副切片示意

以第条路径为例:

首先，单条曲面点集{}中在沿路径初始方向上的端点′、′分别为

(14)

式(14)中:0为点集{}中任一点;′、′均属于点集{}。

第条路径的两个边界平面、为

·(-′)=0

(15)

式(15)中:为路径初始方向；=(,,)为平面上任一点；′为第条路径所对应的单片部曲面点集{}在沿路径初始方向上的端点′、′。

第条喷涂路径的两个端点′与′为第2个主切片平面2，第条路径所对应的单片曲面{}的拟合平面,分别与第条路径的两个边界平面、的交点：

(16)

式(16)中：、、分别为3个平面法向量；、、依次为3个平面上一确定点。

故副切片平面个数′为

(17)

式(17)中：ceil是向上取整函数；为相邻路径点距离；′与′为第条路径两个端点。

副切片平面方向为

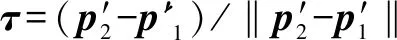
(18)

副切片平面上一确定点′为

{}={′|=′+(-1),∈[1,′]}

(19)

式(19)中:′为第个副切片平面上一确定点。

故第条路径副切片平面集{′}为

{′}={′|·(-′)=0,∈[1,′]}

(20)

式(20)中:′为第个副切片平面;=(,,)为′上任一点。

此时，单片曲面{}中第个点在副切片平面{′}间的位置′为

′=,·′≥0且·′+1<0

(21)

式(21)中，′=表示点在副切片平面′与′+1之间。

最后，将第条路径点集{}代入式(22)即可实现局部曲面{}分片：

{}={|={,′=||′=-1},

∈[1,′]}

(22)

式(22)中:为第条路径中第个路径点所对应的单片曲面。

1.4 基于单片曲面生成喷涂路径点

以第条路径中第个路径点为例。如图5所示，路径点位置(,,)为第2个主切片平面2，第个副切片平面′以及第个路径点所对应的单片曲面点集{}的拟合平面的交点，故将上述3个平面代入式(16)可得路径点位置(,,)。

图5 路径点生成示意

喷枪指向为

(23)

式(23)中:为单片曲面{}拟合平面的单位法向量；为喷枪初始指向。

路径方向为

=(×)×

(24)

式(24)中：为喷枪指向；为路径初始方向。

路径点姿态为

(25)

式(25)中：=×。

1.5 单条路径上外延生成过喷路径点

由于栅格路径在路径换向时会造成曲面边界喷涂不均匀，故需对每条路径增加过喷路径点。

(26)

式(26)中:为过喷距离，=，为圆锥喷枪锥底半径。

至此，遍历所有副切片与所有偶数主切片生成所有单条路径，最后将每条路径首尾顺序连接，即可获得完整喷涂路径。

2 仿真实验

对于规则边缘曲面，不失一般性，以汽车车门主表面作为实验对象，如图6所示，其表面近似曲面且具有规则边缘；对于不规则边缘曲面，不失一般性，以汽车翼子板作为实验对象，如图7所示，其表面近似曲面且具有不规则边缘。喷涂路径分片规划方法中输入参数见表1。

图6 车门点云模型

图7 翼子板点云模型

表1 输入参数

2.1 规则边缘曲面喷涂仿真

对于具有规则边缘的车门，由切片法和文中分片法获取的喷涂路径分别如图8(a)、8(b)所示。由于车门的几何尺寸不能被等距平面整分，可看出切片法对比于分片法缺少一条喷涂路径。

图8 车门喷涂路径示意

仿真方法的细节可在文献[15]中找到，仿真结果分别如图9(a)(b)所示,涂层累积分析结果见表2。在期望涂层厚度为25 μm时，分片法获得涂层厚度误差为4.33 μm，比切片法减小了77.09%；涂层厚度标准差为0.81，比切片法减小了74.37%，分片法在边缘规则的车门生成的喷涂路径所产生的涂层厚度范围比切片法更加集中，提高了喷涂均匀性。

图9 车门涂层厚度累积

表2 规则边缘曲面车门喷涂仿真结果

2.2 不规则边缘曲面喷涂仿真

对于具有不规则边缘的翼子板，由切片法和分片法获取的喷涂路径分别如图10(a)(b)所示。由于切片法只有切平面与曲面相交的地方能产生喷涂路径，易造成曲面边缘处生成的喷涂路径比实际所需的路径短，对比于分片法其每条喷涂路径都偏短。同时翼子板的几何尺寸亦不能被等距平面整分，故可看出切片法对比于分片法缺少一条喷涂路径。

图10 翼子板喷涂路径示意

翼子板喷涂路径喷涂仿真结果分别如图11(a)(b)所示,涂层累积分析结果见表3。在期望涂层厚度为25 μm时，分片法获得涂层厚度误差为4.03 μm，比切片法减小了77.42%；涂层厚度标准差为0.76，比切片法减小了73.15%。切片法生成的喷涂路径由于不够完善导致在每条路径边缘处喷涂不均匀，而分片法在边缘不规则的翼子板生成的喷涂路径所产生的涂层厚度范围比切片法更加集中，提高了喷涂均匀性。

图11 翼子板涂层厚度累积

表3 不规则边缘曲面翼子板喷涂仿真结果

3 结论

提出一种曲面边缘均匀喷涂的路径分片规划方法，仿真结果表明：

(1)该方法可直接在点云模型上进行操作，实现了喷涂路径自动规划。

(2)该方法对于具有规则和不规则边缘的曲面均可实现曲面均匀喷涂路径规划，避免了切片法生成的喷涂路径在曲面边缘处喷涂不均匀的弊端，提高了喷涂均匀性。