一种平面二自由度并联机构工作空间分析

2022-09-19张蔚陈浩

机床与液压 2022年5期

张蔚,陈浩

(常州纺织服装职业技术学院机电工程系，江苏常州 213164)

0 前言

并联机构在动平台与定平台之间通过至少两条以上独立的开环运动支链相连接，具有承载能力强、结构刚度大、运动精度高等优点，在工业界有着广泛的应用。在多轴加工中心、航空模拟器等一些特殊应用领域，类似Stewart机构等六自由度并联机构受到许多学者和工程技术人员的青睐；然而，无显式运动学正解、控制复杂、设计制造成本高等问题，也成为了其不可回避的技术难点。事实上，在许多运用场合下，并不完全需要过多的运动自由度，少自由度并联机构更具经济适用性和工程推广价值。

相比传统串联机构，并联机构的工作空间相对较小，因此，工作空间是评价并联机构使用性能的一项重要指标。石梦蕊、赵新华基于运动学反解方程，在给定的设计参数搜索空间内，通过扫描搜索法获得了3-PRRRR机构的工作空间；类似地，周毅钧等采用蒙特卡洛方法完成了2RPU/2SPS机构工作空间的计算。上述搜索方法虽能够在一定设计变量取值空间内计算出并联机构的工作空间，但仍存在一定的局限性：一方面，直接搜索方法计算量较大；另一方面，也无法掌握工作空间指标在全局变量空间内的变化趋势。

GAO、LIU等提出了一种无量纲模型，可将机构运动学参数完整设计空间转化到一个有限设计平面内，通过绘制相应的平面性能图谱获得并联机构工作空间性能的全局变化规律，并以此为相关机构参数的优化提供直观的设计依据。

本文作者以一个平面二自由度并联机构为例，首先通过运动学计算获得了机构的两种反解模型，并完成了奇异分析，而后重点针对两种反解模型下机构工作空间可能存在的所有形式进行了讨论，最终通过建立机构运动学参数的无量纲模型，绘制该机构最大矩形工作空间的性能图谱，并指导了机构参数的优化设计。

1 机构描述

二自由度平面并联机构如图1所示，由一个固定基座、一个动平台、两个滑块和两条运动支链组成。每条运动支链包含3根等长连杆，每根连杆的两端均通过虎克铰分别连接到动平台和滑块上。

图1 平面二自由度并联机构

图2为该机构在两个相互正交平面内的投影视图。从视图A中可以看出，两条运动支链对称分布，连同动平台与滑块、固定基座构成一个封闭对称的结构；同一运动支链中的3根连杆的投影互相平行，与动平台和滑块组成一个过约束平行四边形机构，这样确保了动平台运动过程中始终处于水平状态。在视图B中，布置在同一侧的3根连杆投影重合，与滑块和动平台构成一个等腰梯形结构。由于虎克铰的约束，该等腰梯形结构保持稳定，不会导致动平台在视图B平面内的翻转运动。基于以上结构特点，通过驱动两个滑块的水平移动，可以使得动平台在视图A中做二自由度的平面运动。

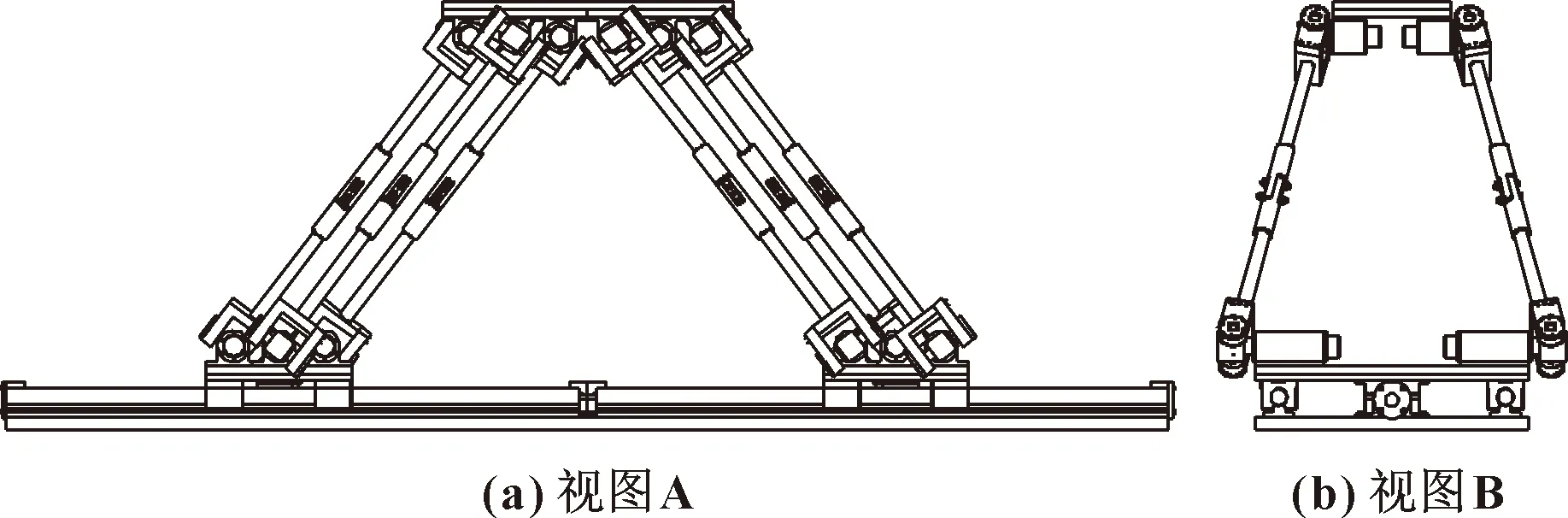
图2 平面二自由度并联机构投影视图

2 机构运动学分析

二自由度平面运动机构的结构简图如图3所示。为方便以下分析，建立一个固定坐标系-，其原点固定在基座的中心处。动平台的中点记为点，即为整个机构的运动输出点。由于运动支链中的平行四边形结构，使得在运动平面内，相同运动支链中的3根连杆的运动情况相同，因此，可以将每条运动支链简化为连杆 (=1,2)。在坐标系-中，各铰接点、(=1,2)和运动输出点的坐标分别记为(,)、(,)和(,)。其中，运动输入量为两滑块的水平位置，即(=1,2)；运动输出量为(,)。

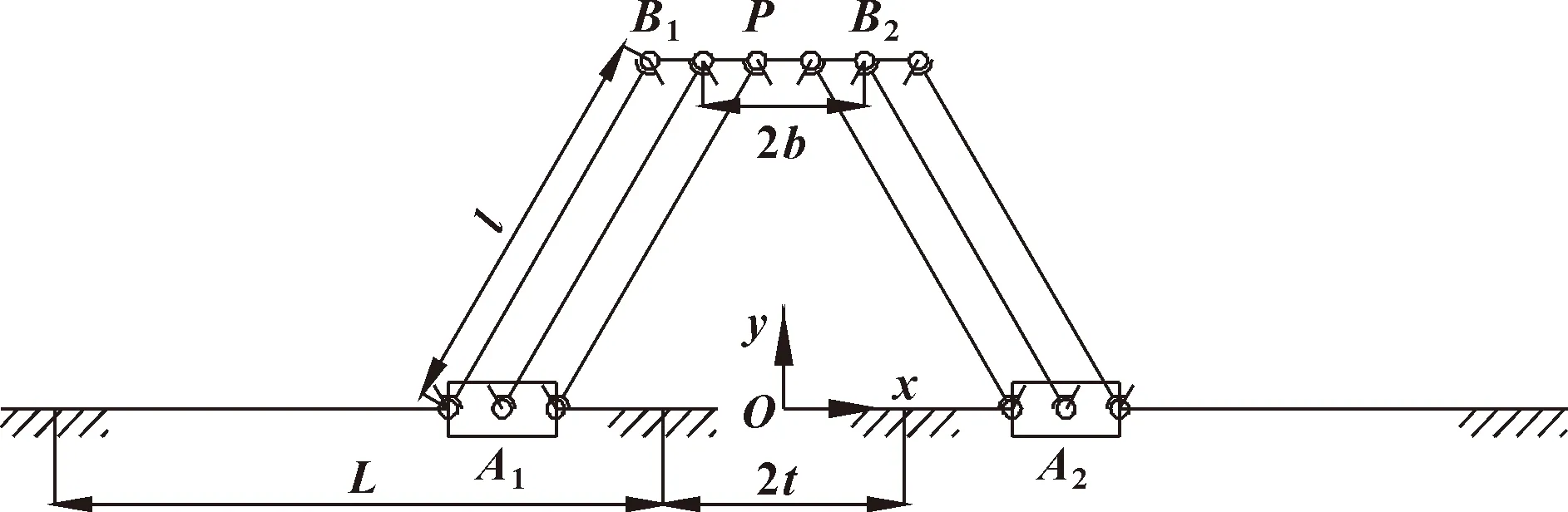
图3 机构运动简图

动平台上铰点之间的长度记为2，称为动平台的有效长度；(=1,2)的长度记作，称为连杆的投影长度；两个滑块在两条导轨上的最小间距记为2；每个滑块在单条导轨上的实际运动长度记作。所有的长度尺寸参数大于0。因此，运动输入量(=1,2)的变化范围为

1∈[--,-]，2∈[,+]

(1)

为了能够实现机构的正常装配，还必须满足以下装配约束条件

|-|<

(2)

2.1 运动学正解

由图3可以得到机构的运动矢量方程

=++=1,2

(3)

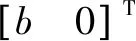
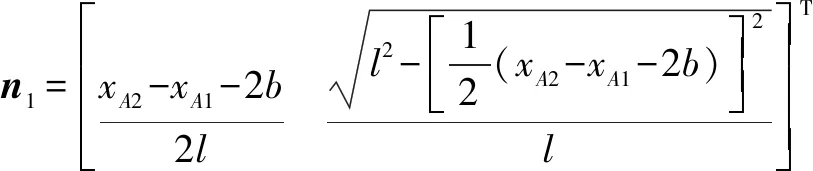
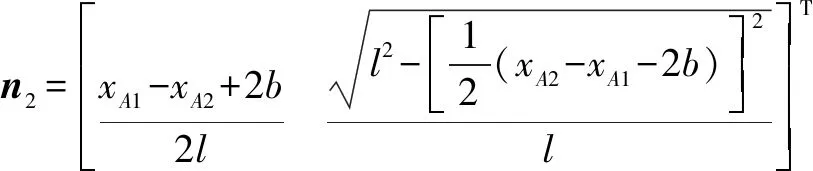
因此，式(3)可进一步转化为正解方程

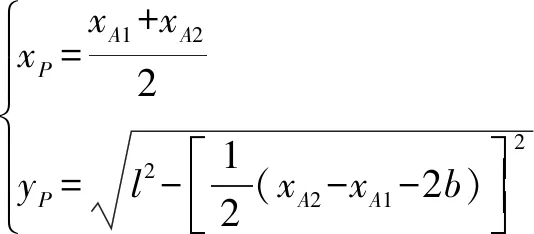
(4)

由式(4)可以看出，该机构运动学正解唯一。

2.2 运动学反解

将式(4)中动平台坐标(,)作为已知，滑块坐标(=1,2)作为未知，可进一步获得机构运动学反解方程

(5)

从式(5)中可以看出，由于=±1，使得机构存在两种运动反解情况。当=+1时，机构的反解模型如图4(a)所示，称为第一种反解模型；当=-1时，机构的反解模型如图4(b)所示，称为第二种反解模型。

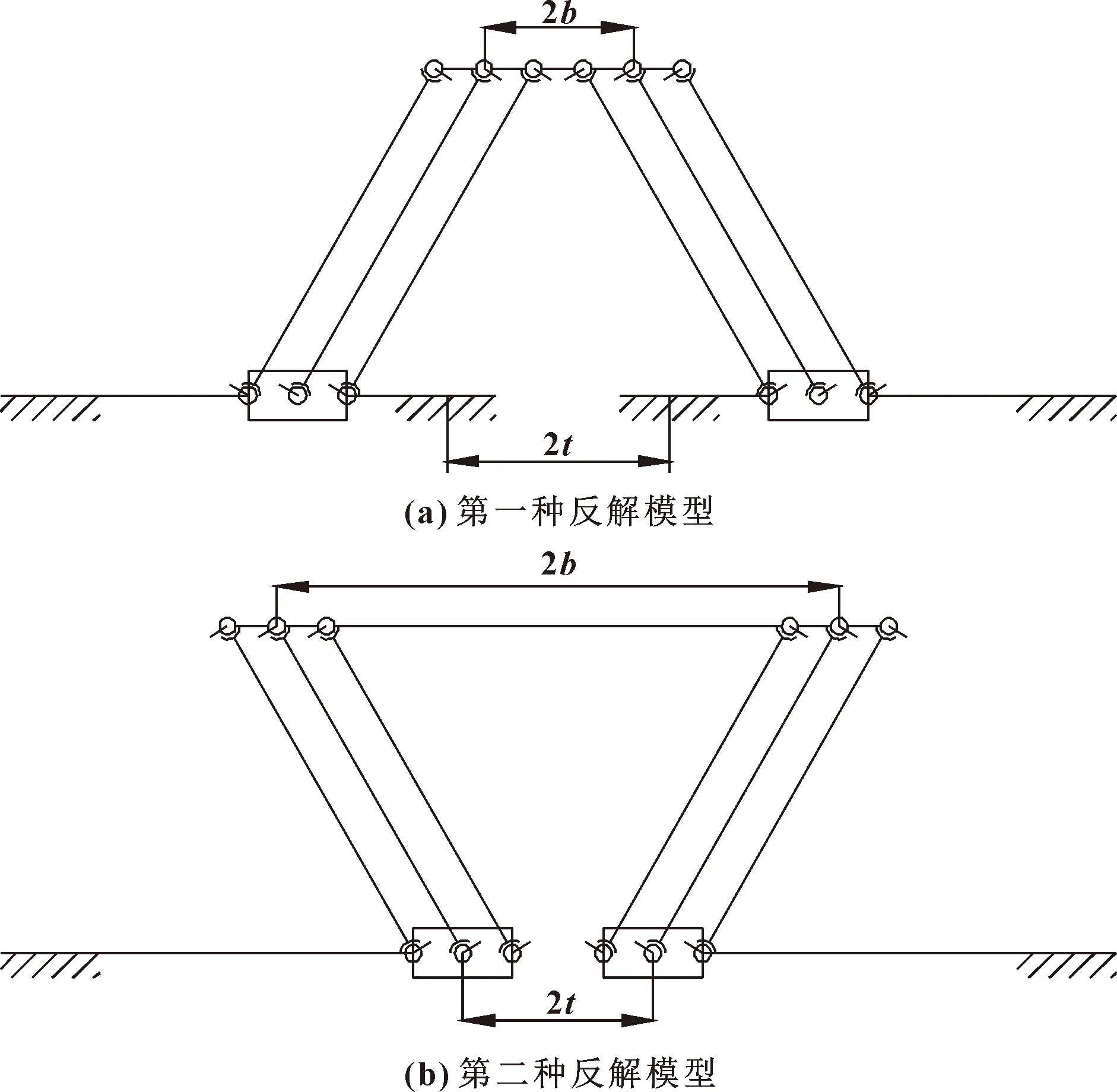
图4 两种反解模型

从图4中不难看出，能够出现第一种反解模型的条件为+>；而仅出现第一种反解模型的约束条件为>。类似地，能够出现第二种反解模型的条件为<；而仅出现第二种反解模型的约束条件为+<。

对比两种反解模型，不难看出机构在第一种反解模型状态下时，机构动平台宽度相对两滑块之间的间距较小，其承受的载荷全部在两滑块之间，因此具有较好的稳定性；而工作在第二种反解模型下时，机构动平台宽度相对两滑块之间的间距较大，其承受的载荷有部分在两滑块之外，此时机构的稳定性较差。

2.3 奇异分析

由于机构的奇异会导致其可控性和刚度变差，因此必须对机构进行奇异性分析，以避免机构在运动中出现奇异位形。

反解方程式(5)可变形为

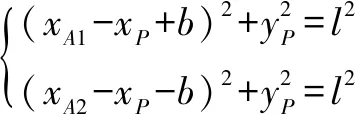
(6)

对上式求导，可进一步获得:

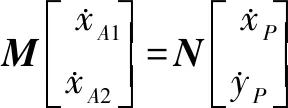
(7)

其中:

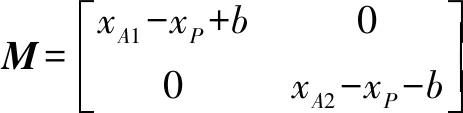
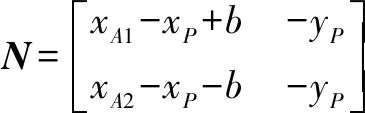
从而可以获得运动雅可比矩阵:

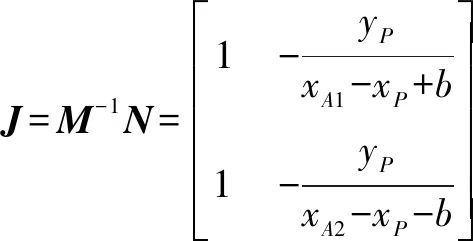
(8)

在并联机构中，奇异位形出现在当det()=0、det()=0或det()和det()同时为0的情况下。以下针对各种奇异位形的出现条件进行具体分析。

(1)det()=0

由矩阵的表达式可以得到出现这种奇异位形的条件

(1-+)(2--)=0

(9)

故当1-+=0或2--=0时机构处于该奇异位形状态。由机构的对称性可知，1-+=0等价于2--=0，因此，这种奇异位形出现在当两滑块之间的距离2-1等于动平台的有效长度2的情况下。此时，机构的动平台、两条运动支链以及固定基座构成一个平行四边形结构，在这种奇异位形下，机构将失去刚度，且变得不可控，如图5所示。在此把这种奇异位形称为第一类奇异位形。在机构正常工作中应该避免出现这种奇异位形状态。

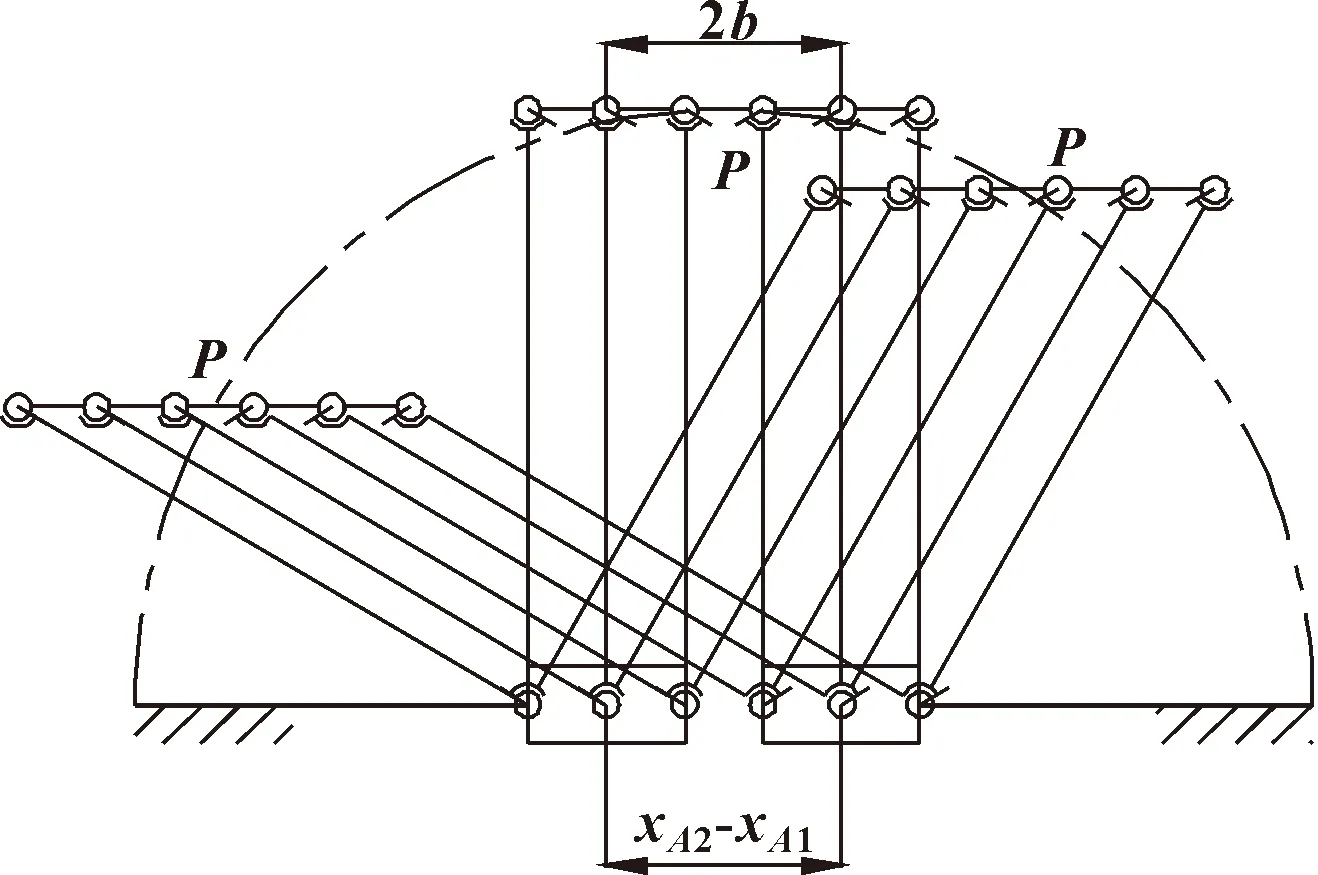
图5 第一类奇异位形

(2) det()=0

由矩阵的表达式可以得到出现这种奇异位形的条件

(2-1-2)=0

(10)

故当=0或2-1-2=0时机构处于该奇异位形状态。不难看出，第二种条件2-1-2=0包含于第一类奇异位形出现的条件；另外，由第一种条件=0可知，当连杆(=1，2)处于水平状态时也同样出现奇异，由于机构存在两种反解模型，因此该奇异状态也存在两种情况，如图6所示。在这种奇异状态下，机构将被锁死，处于不可移动的状态。在此把这种奇异位形称为第二类奇异位形。为了避免这种奇异位形，在机构运动中要尽量保证较大的压力角，避免动平台接近其最低位置。

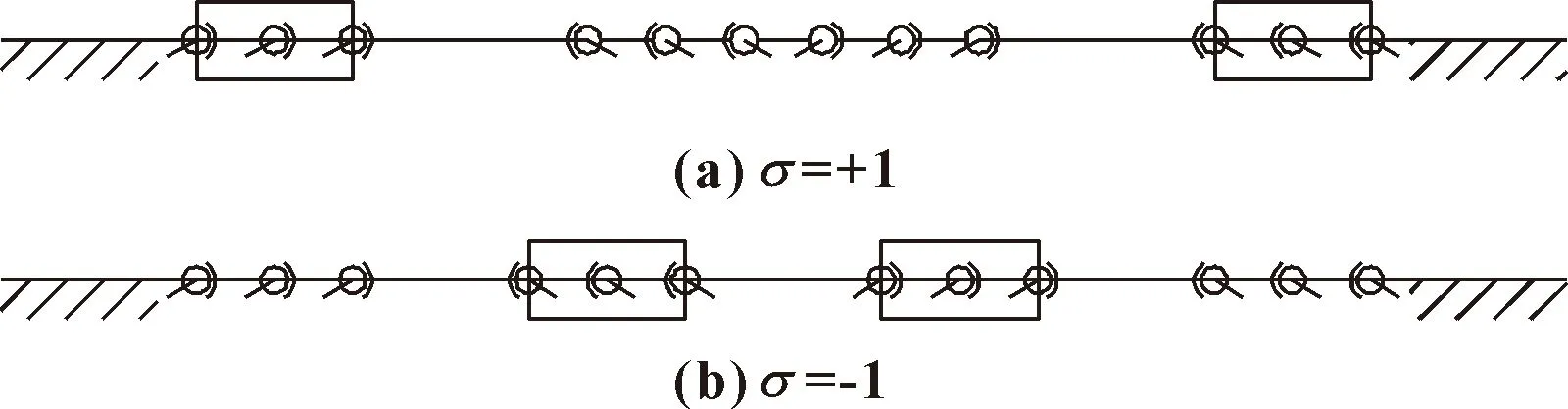
图6 第二类奇异位形

(3)det()=0且det()=0

由于第一类奇异位形的出现条件，即连杆(=1，2)处于竖直状态，也同时是第二类奇异位形的出现条件之一，因此，在该条件下，将导致矩阵与同时奇异。故此情况下奇异位形属于第一类奇异位形的特殊情况。

3 理论工作空间

该平面二自由度机构的理论工作空间是两个滑块在式(1)确定的运动范围内变化时，点在运动平面内所覆盖的面域。将式(1)中两个滑块的运动极限位置分别代入式(6)可以得到4个极限圆、、和，其圆心分别为(-+,0)、(-,0)、(--+,0)和(+-,0)。其中，圆和称为内极限圆，圆和称为外极限圆。该机构的理论工作空间就是由这4个极限圆确定的，图7所示阴影部分面域即为其理论工作空间。

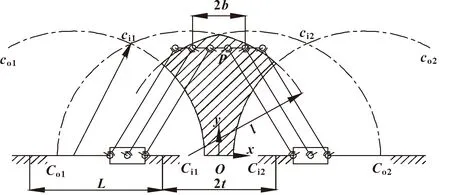
图7 理论工作空间

由上文分析可知该机构存在两种反解模型，而第一类奇异位形就发生在两种反解模型相互转换的临界姿态下。为避免第一类奇异位形的出现，就必须避免机构在工作中发生两种反解模型之间的姿态转换。因此，以下分别针对在两种反解模型下的机构理论工作空间进行讨论。

3.1 第一种反解模型下的理论工作空间

当机构工作在第一种反解模型时，在满足约束方程(2)和+>的前提下，4个极限圆圆心的位置关系条件可以总结为以下4种条件集合，见表1。

表1 第一种反解模型下极限圆位置关系条件

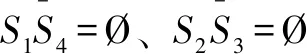
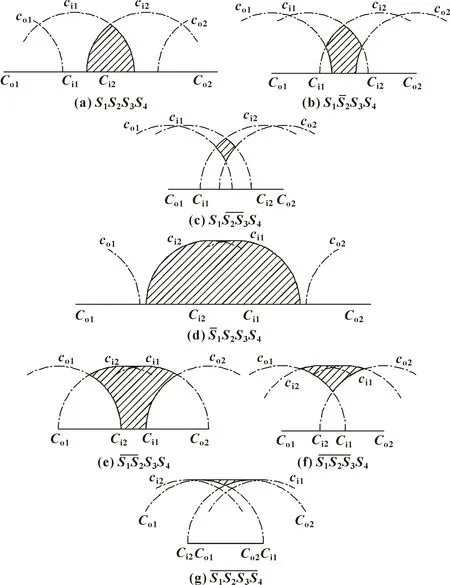
图8 第一种反解模型下的理论工作空间

从图8中可以看出，在(a)(b)(c)3种条件下，机构由于尺寸条件的限制，在其工作空间中将不可能出现第一类奇异位形，尤其是在条件(c)下，在其工作空间中也不会出现第二类奇异位形；在(d)(e)(f)(g)4种条件下，在其工作空间中可能出现第一类奇异位形，即机构运动可能出现两种反解模型之间的转换，因此，必须在两滑块的运动控制上限制其接近第一类奇异位形。另外，在条件(f)和(g)下，机构在其工作空间中不会出现第二类奇异位形，但对于(d)和(e)两种条件而言，则可能出现第二类奇异位形，这就需要通过两滑块的运动控制来保证较大的压力角，使其回避第二类奇异位形。

3.2 第二种反解模型下的理论工作空间

当机构工作在第二种反解模型时，在满足约束方程(2)和<的前提下，4个极限圆圆心的位置关系也可以总结为以下两种条件集合，见表2。

表2 第二种反解模型下极限圆位置关系条件

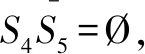
图9 第二种反解模型下的理论工作空间

从图9可以看出：在(a)和(b)两种条件下，机构在其工作空间中可能出现第一类奇异位形，但将不会出现第二类奇异位形；在条件(c)下，两类奇异位形将都不会出现。

4 工作空间性能图谱

工作空间是衡量平面二自由度并联机构工作性能的一项重要指标。对比图8和图9中两种反解模型下机构的工作空间可以看出，在机构总体尺寸相当时，工作在第一种反解模型下的理论工作空间要明显大于第二种反解模型，即机构在第一种反解模型下的工作姿态更具有工程实用意义。因此，主要针对机构在第一种反解模型下的工作空间进行讨论。

4.1 最大矩形工作空间

从图8可以看出，平面二自由度并联机构的工作空间呈现不规则形状。在实际运用当中，一般采用其内接最大矩形工作空间作为衡量指标。

对于图8所示各种情况，工作空间内接矩形面积的计算公式存在以下3种形式

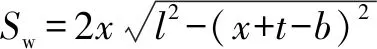
(11)

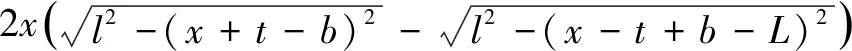
(12)

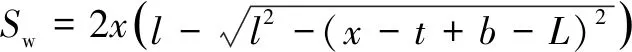
(13)

对于图8(a)和8(d)，可按式(11)计算；对于图8(c)，可按式(12)计算；对于图8(g)，可按式(13)计算；对于图8(b)，其工作空间内接矩形存在两种形式，分别可按式(11)或(12)计算；对于图8(e)，其工作空间内接矩形存在3种形式，分别可按式(11)、(12)或(13)计算；对于图8(f)，其工作空间内接矩形也存在两种形式，分别可按式(12)或(13)计算。

4.2 量纲一化参数模型

从上述机构运动学分析中可知，该平面二自由度并联机构的主要运动学参数包括、、和，其中，影响机构运动学性能的独立参数为、和-(在第一种反解模型中>)。由于这些参数的实际取值范围为无穷空间，为便于在一个有限设计空间内对所有参数情况进行研究，采用一种量纲一化参数模型。通过下式可以将机构独立参数转化为量纲一化参数：

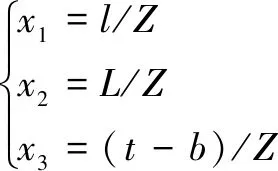
(14)

其中:

=++(-)

根据式(14)可知：

++=1

(15)

由机构装配约束条件及第一种反解模型的存在条件可知:

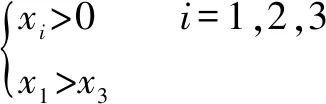
(16)

根据式(14)—(16)可以构建出量纲一化自变量的有限设计空间，如图10(a)中所示的△围成的阴影面域。

进一步假设

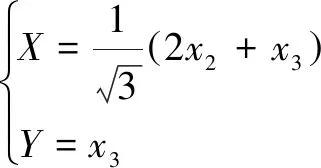
(17)

通过式(17)可将自变量设计空间内任意一点，由原先的-坐标系转化到-坐标系内，从而使得对机构的运动学性能进行平面图谱表征成为可能，如图10(b)所示。

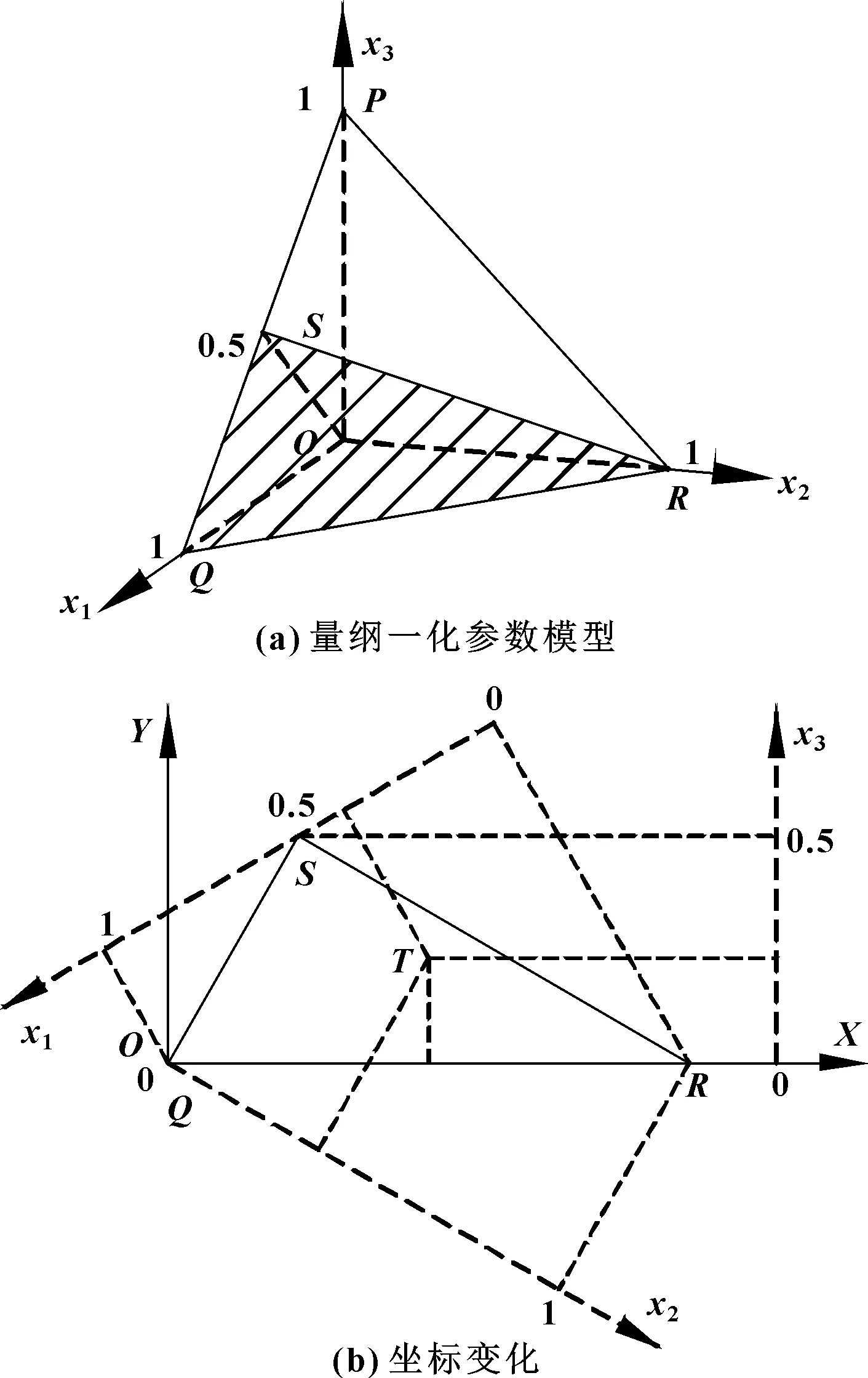
图10 量纲一化参数模型

4.3 性能图谱

将量纲一化运动学设计参数、和代入式(11)—(13)，可以在图10(b)所示坐标系内，获得最大矩形工作空间关于变换坐标和的性能图谱，如图11所示。

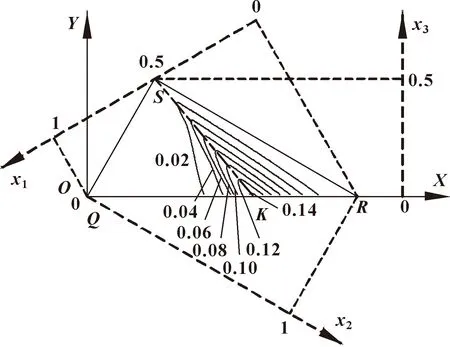
图11 最大矩形工作空间性能图谱

从图11可以看出：最大矩形工作空间的等值曲线中存在一条明显的脊线，并在脊线两侧沿正交方向逐渐减小；在脊线上沿方向最大矩形工作空间逐渐增大，其中点为峰值点，其在-坐标系内的坐标为(0.71,0)，对应的转换前量纲一化参数分别为=0.385 1、=0.614 9、=0。即在机构总体尺寸一定(为常数)的情况下，当=，且∶=0.385 1∶0.614 9时，机构可获得最大矩形工作空间。