面向六自由度移动机械手底座位置优化方法

马金茹，高文华，祁宇明

(1.北京电子科技职业学院汽车工程学院，北京100176；2.天津科技大学，天津 300222;3.天津职业技术师范大学，天津 300222)

0 前言

随着机器人技术的快速发展，移动机械手由于具有良好的机动性和灵活性，可以灵活地到达不同的工作位置，完成复杂的加工任务，在大型复杂零件的加工中具有广阔的应用前景。然而机器人在任务空间中的性能分布是高度非线性的，这使得确定最合适的基座位置 (BP)非常困难。因此有必要建立一种有效的移动机械手BP优化方法，快速准确地确定最优BP，这对装配成本的降低具有重要意义。

移动机械手基座优化能够有效提高任务的完成效率和质量，受到了众多研究者的关注。为了实现更高的生产效率，面向任务的目标函数被应用于机器人基座优化问题，如最短路径和最小循环时间、最低能耗。在大多数情况下，基座位置优化关注的是提高任务的完成质量，这与机器人的性能密切相关。因此，现有的许多方法主要是为了提高机器人的性能，蒋毅等人研究了某四自由度机器人基座优化方法，通过有限元软件对机器人结构进行仿真，分析了机器人结构参数对机器人动态特性的影响，在此基础上以基座基频为优化目标确定了最优基座位置。张崇等人研究了风电塔筒机器人电机基座优化问题，建立了以电机基座的动态载荷为目标的有限元拓扑方法，确定了电机基座轻量化目标的最佳位置。REN等提出了优化移动机械手基础位置的算法，该算法考虑到机械手的物理限制和奇异性，通过实验验证了该算法的优越性。YU等针对移动涂装机器人，建立近似解耦模型，在此基础上提出了机械手底座位置优化方法，考虑了定位约束、定向约束和奇异回避约束，将BP优化问题转化为路径准则的标准不等式约束优化问题，通过实验验证了所提方法的有效性。

以上主要方法为机器人系统的底座位置(BP)优化提供了重要参考，但基本上都是关注机器人的运动能力和运动性能，很少考虑机器人的刚度性能。鉴于机器人的刚度性能通常对加工质量有一定的影响，作者提出一种同时考虑机器人运动学和刚度性能的底座位置BP优化方法，以最大全局刚度性能评价指标为目标函数，以关节距离、关节速度、奇异避免和碰撞避免为约束条件，建立优化模型，采用稀疏均匀网格分解寻找优化模型的有效初值，通过序列二次规划(SQP)方法最终求解基座的最优位置。

1 运动学和刚度性能指标

设计合适的性能评价指标是移动机械手BP优化的前提。以六自由度机器人为例，分别介绍用于BP优化的动力学和刚度性能指标。D-H参数模型和数据分别如图1和表1所示，=0.3 m,=0.7 m,=0.28 m,=0.893 m,=0.2 m。

图1 D-H参数模型

表1 机器人的D-H参数

1.1 运动性能指标

雅可比矩阵的条件数是评价运动学性能的有效方法。将采用基于Frobenius范数的运动学雅可比矩阵的条件数()作为量化奇点距离的方法，该指数称为动静调节指数(KCI)，定义为

(1)

其中：tr(·)为矩阵的迹；为具有相同物理单位的齐次雅可比矩阵，定义为

(2)

其中：、、分别为3×3的单位矩阵、3×3的零矩阵和雅可比矩阵;为特征长度，可通过求解的最大值得到。的取值范围为(0,1]，值越高，机器人的运动学性能越好，特别是当=1时，雅可比矩阵的所有奇异值都相等，说明该机器人具有最佳的运动学性能。反之，当=0时，雅可比矩阵的最小奇异值趋近于零或最大奇异值趋近于无穷大，机器人的运动性能将恶化。

1.2 刚度性能指标

(3)

其中：diag(·)为对角化函数；(=1,2,…,6)为第个关节刚度值(N·m/rad)，可通过有限元分析方法得到。对于六自由度机器人，关节刚度矩阵为

=diag([2.03×106.02×101.91×10

0.45×100.22×100.07×10])

(4)

根据柔度模型，端部执行器(EE)的位移与施加在其上的扳手关系可以定义为

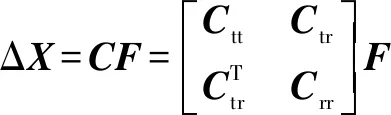
(5)

其中:是柔度矩阵，即的逆；Δ是由EE的平移和转动位移组成的6×1位移矢量；是施加在EE上的力和力矩组成的6×1扳手矢量。、、分别为3×3平移子矩阵、耦合子矩阵和转动子矩阵，其单位分别为m/N、rad/(N·m)和rad/N。此外，考虑到在加工过程中，可忽略刀具的转动位移、平移位移和作用在刀具上的扭矩，则可将式(5)重新定义为

Δ=

(6)

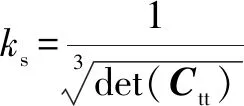
(7)

指标可以很好地表征机器人在一定关节角度下的刚度性能，的值越大，机器人的刚度性能越好。但仅为局部性能指标，不能直接用于评价机器人在加工任务中的全局刚度性能。基于此，提出了一种面向任务的全局刚度性能评价指标，其定义为

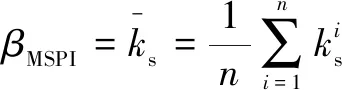
(8)

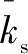
2 优化问题

BP优化的目标是在保证机器人运动学性能的前提下，尽可能地提高机器人的刚度性能。图2所示为移动机械手加工系统模型。

图2 移动机械手加工系统

(9)

其中:=×。

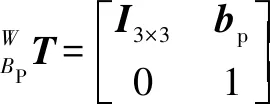
(10)

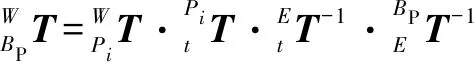
(11)

(12)

3 优化模型与方法

最优BP算法应满足两个要求：(1)机器人在每个关键加工点的刚度应尽可能高，以提高加工质量；(2)机器人应始终具有良好的运动性能，以保证其刀具能沿给定的加工路径平稳、准确地运动。

3.1 优化模型

优化模型的建立包括两个方面:(1)确定目标函数;(2)明确约束条件。考虑到基座BP优化的目的是尽可能提高机器人的刚度，将目标函数定义为最大全局刚度，即MSPI的最大化。因此目标函数的表达式为

(13)

(1)关节距离

由于机械结构的限制，机器人各关节角,通常有明确的上、下限，即max和min(=1,2,…,6)。因此，关节距离约束的函数形式可以定义为

()=(,-min)(,-max)≤0

(14)

其中:=[,1,,2,,3,,4,,5,,6]，=1,2,…,。

(2)关节速度

(15)

(3)奇异回避

当机器人处于或接近奇异位形时，机器人的自由度将丢失，进而影响机器人的控制精度。因此，在加工任务中，机器人必须远离奇异位形，约束的函数形式可以定义为

()=()-≥0=1,2,…,

(16)

(4)避碰

在加工过程中，必须避免机器人与周围环境之间的碰撞。为简化避碰模型，本文作者采用工件和机器人的简化模型，如图3所示，工件与机器人之间的碰撞检测将变得更加简单。如果工件简化模型中的所有点都不在机器人简化模型的任何规则几何内，则认为机器人与工件之间不存在碰撞，否则，就会发生碰撞。假设工件简化模型中有个点，为其中之一。同时，在机器人的简化模型中有个规则几何对象，是其中之一，的质心为。考虑到的位置坐标是机器人关节角的函数，则碰撞检测约束的函数形式可以定义为

()=(,)≥0=1,2,…,；=1,2,…,

(17)

式中:(·)为点到正则几何曲面的最小距离。

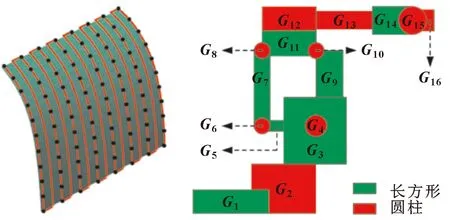
图3 工件和机器人的简化模型

如图4所示，当规则几何为球面、圆柱体和长方体时，(·)可分别定义为公式(18)—(20)，结果如下：

(,)=dist(,)-·

(18)

(19)

(20)

式中:、、、为正则几何的尺寸参数；为大于1的安全系数，推荐值为1～1.5;距离dist(·)是两点之间距离的函数。此外，如果点到规则几何曲面的最小距离(记为)为正，则点不在几何曲面内部，否则点在几何内部。

图4 碰撞检测原理

此外，为了保证优化方法的效率，基座BP的搜索范围将受到限制。设BP上下限为=[,,],=[,,],优化模型可定义为

max(,)

(21)

在式(21)所示的优化模型中，涉及到变量和，并且存在多个非线性约束，为了使优化模型更容易求解，有必要对其进行合理简化。

由式(21)可知，机器人关节角度实际上是的函数。与此同时，约束条件(·)到(·)也是关节角的函数。因此，可以通过设计集成的IK算法来实现优化模型的简化。集成的IK算法如算法1所示，其中IKflag为BP是否有效的标志，ikopt(·)为多个逆解的首选函数，且有效的BP值必须满足(·)到(·)的约束条件。

算法1：

01:θ=zeros(n,6),IKflag=1

02:for i=1∶n

05:if g(θ)>0

06:IKflag=0,break

07:end

09:IKflag=0,break

10: end

11: if g(θ)<0

12:IKflag=0,break

13: end

14:if g(θ)<0

15:IKflag=0,break

16: end

17:end

18:return θ and IK

所有有效的BP集合称为BP的可行域(简称RBP)，根据算法1，目标函数可以重新定义为

max=IKflag·(,)

(22)

最终优化模型为

max()

s.t.≤≤

(23)

3.2 优化方法

方程(23)是标准的有界非线性优化模型，可以采用内点法、序列二次规划(SQP)法等多种方法求解，这些优化算法通常需要一个合适的初始值。在求解过程中，首先通过稀疏均匀网格分解法确定合适的初值，然后选择SQP法计算最优值。具体的求解方法如下：

步骤1，确定初始基座BP的

由于约束条件(·)到(·)的存在，在笛卡尔子空间中，RBP的分布具有不规则和不连续的特征，因此有效的初始值应该满足的条件是：(1)在RBP内部；(2)在最优BP所在的连通域；(3)靠近最优BP。考虑到这些要求，采用稀疏网格均匀分解方法将是一种较好的方法，不仅可以确定合适的初值，而且可以缩小最优BP的搜索范围。该方法的原理图如图5所示。

图5 稀疏均匀网格分解

算法2：

01:b=fix(b/a)·a

03:β=0

04:for i=1∶m

05: for j=1∶n

06: for p=1∶k

07:b=b+a·[i-1,j-1,p-1]

08:β(i,j,k)=F(b)

09: if β(i,j,k)>β

10: β=β(i,j,k)

11: maxind=[i,j,k]

12: end

13: end

14: end

15:end

16:b=b+a·(maxind-[1,1,1])

17:return band β

进一步，由图5可知，最优BP搜索范围()可以确定为：=[,]，其最小值和最大值表示式分别为=-[;;0],=+[;;0],其中是网格的边长或分辨率。同时，为了保证的有效性和算法2的计算效率，在实际应用中将设为0.1 m或0.2 m。

步骤2,确定最优BP的

SQP是非常适合求解非线性约束优化模型的经典优化方法，已集成到各种通用优化算法工具箱或软件包中，如MATLAB优化工具箱、IPOPT等。因此，在确定之后，使用SQP方法来求解是一个很好的选择。在这里，利用MATLAB优化工具箱中的fmincon(·)函数求解最优BP，其调用格式为

=fmincon(-(),,,,,,,,option)

option=optimoptions(@fmincon,′Algorithm′,′sqp′)

根据MATLAB的SQP方法，可以精确求解。

4 模拟和实验

为了说明基座BP优化方法的有效性，将分别通过仿真和实验进行验证。仿真结果主要说明了基座BP优化方法的有效性，即该优化方法能够找到满足～约束且MSPI最大的基座位置，实验主要用于验证性能指标MSPI与加工质量之间的对应关系。

4.1 模拟环境

以风机叶片表面抛光仿真为应用背景，如图6所示，风机叶片的整体尺寸可以达到59.5 m×2.5 m×4.0 m，远远超出了机械手的操作范围。因此，通常将风机叶片表面预先划分为几个待加工的子区域。绿色区域是其中的一个子区域，其大小为1.6 m×0.3 m×1.2 m，及其边界尺寸参数=[-0.80,0.80,-0.34,0.07,1.44,2.66] m。机器人最大距离可达=1.90 m，底架高度为=0.75 m，则的搜索范围可为=[-1,1.10;-2.20,-0.30;0.75,0.75] m。此外，机器人确定的约束条件如表2所示。

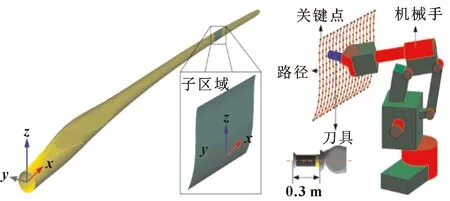
图6 风机叶片表面磨削仿真环境

表2 g1(·)到g4(·)的约束

4.2 仿真结果

如图7所示，给出了算法2得到的MSPI等高线图，同时图中也标出了准RBP的边缘和最优BP精确搜索范围的边缘。另外，图中白色部分表示该区域没有有效的BP，但准RBP中的白色部分可能仍有有效的BP，这主要是由于网格分辨率较低所致。

图7 平均刚度性能指标(MSPI)等值线图

根据等高线地图，可以确定初始BP为=[-0.10;-1.80;0.75] m,精确搜索范围=[-0.2,0.00;-1.90,-1.70;0.75,0.75] m。然后最优的BP可以通过SQP方法得到，其值为=[-0.099 4;-1.728 8;0.750 0] m。

为了进一步证明优化方法的有效性，分别给出了最优BP处各关键点的关节角度、关节速度、和的分布图，如图8—图11所示。

图8 加工路径上各关键点Pi的关节角度

图8中，蓝线表示加工路径上各关键点的关节角度，红线表示关节角度的上下限。图9中，蓝线表示加工路径上各关键点的关节角速度，红线表示关节角速度的正负最大值。在图10中，蓝线表示机器人在加工路径上各关键点处的KCI值，红线表示KCI的最小值。在图11中，曲线分别表示了机器人简化模型中加工对象的简化模型与规则几何(=1，2，…，15)之间的最小距离，的分布如图3所示。从这些图形中可以看出:机器人的关节角度和关节角速度均在限定范围内，机器人的KCI值均大于最小值，所有关键点上(=1，2…，15)的值均大于0。

图9 加工路径上各关键点Pi的关节角速度

因此，在最优BP算法中，结果满足(·)～(·)约束条件，保证了机器人的运动性能。上述分析表明了所提出的基座BP优化方法的正确性，该方法能有效地找到全局刚度性能最大的基座位置，满足实际应用中需要考虑的所有运动约束条件，这对于提高移动机械手的操作性能具有重要意义。

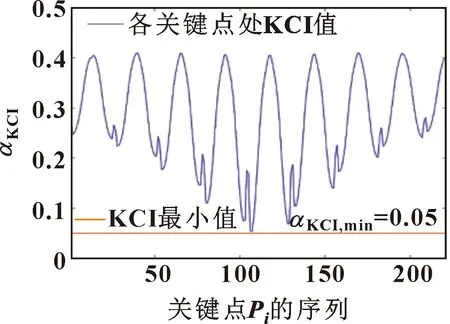
图10 每个关键点Pi的KCI

图11 Gj所有关键点的dmin

5 结论

针对六自由度机械手在大型复杂零件的加工能力，提出一种面向移动机械手加工基座位置优化方法，其目标是在保证机器人运动性能的同时，优化机器人的刚度性能。建立了机械手运动性能指标和全局刚度指标，在此基础上综合考虑了机械手关节距离、关节速度、奇异回避和避碰等多约束条件，通过采用稀疏均匀网格分解和序列二次规划(SQP)方法对机械手最优基座位置进行求解。最后通过仿真分析和实验结果验证了该优化方法的有效性。