计及混合间隙的高速精密机构非线性动态响应分析
2022-09-19陈宇武凯仲太生王禹孙宇
陈宇,武凯,仲太生,王禹,孙宇
(1.南京理工大学机械工程学院,江苏南京 210094;2.江苏扬力集团,江苏扬州 225127;3.江苏理工学院机械工程学院,江苏常州 213001)
0 前言
随着社会的发展和科技的进步,市场对零件的加工精度和质量提出了更高的要求,对机械传动系统的设计要求日益提高,以实现更高运动精度以及良好的稳定性。在机械系统中,由于碰撞磨损和制造误差,都无法避免运动副零件之间的间隙产生。间隙的存在将会造成杆件的分离和碰撞,从而引起机构产生振动、噪声。含间隙高速精密动力学研究对提升机械装备性能,实现复杂装备振动、噪声的有效控制,以及高精密机械装备设计技术的升级具有重要的意义。
针对含间隙机构动力学问题,国内外众多学者进行了相关研究。例如,FLORES等针对含间隙运动副接触碰撞过程中的接触类型和约束条件进行了讨论,采用Moreau时间步长法对其线性求解问题进行了描述,并将其运用到含间隙机构动力学性能分析中。白争锋等考虑非线性刚度系数对接触碰撞过程的影响,提出一种含间隙转动副接触碰撞力模型,并将其应用到含间隙曲柄滑块模型中。ZHANG等建立一种含间隙转动副的冗余驱动机构动态特征分析模型,采用分部积分法对其进行求解,并获得间隙对机构动力学性能的影响。SALAHSHOOR等基于多尺度法建立了含多间隙多体系统动力学分析模型,研究了机械系统的非线性振动特征。TIAN等考虑构件柔性特征影响,建立了含不确定性间隙转动副的机构动力学分析模型,计算结果表明间隙和构件柔性对机构非线性动力学影响较大。目前,考虑混合间隙作用下高速精密机构动态特性相关研究很少。本文作者针对以上情况,基于多体动力学理论、非线性接触碰撞理论和库仑摩擦理论,建立一种含混合间隙的高速精密机构动力学模型;将其引入到高速精密压力机传动系统模型中,结合高速精密机构动力学性能实验,分析了计及混合间隙的高速精密机构的非线性动态响应特性。
1 含间隙机构动力学建模
1.1 含间隙运动副运动学建模
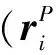
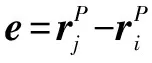
(1)
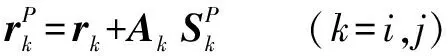
(2)
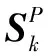
轴与轴承在偏心方向上的单位法矢量为
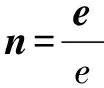
(3)
如图1(b)所示,当偏心矢量的大小大于轴承间隙时,轴承与轴在偏心矢量的延长线上会发生接触,即接触点为和,该点的位置矢量和速度矢量可表示为
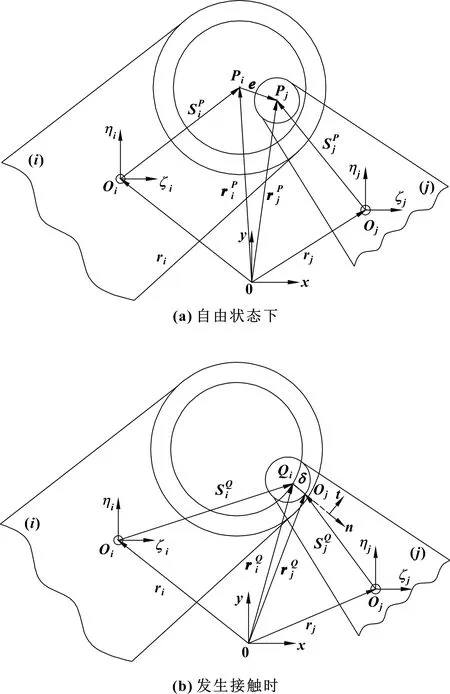
图1 转动副间隙模型
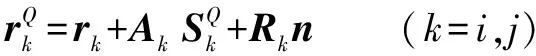
(4)
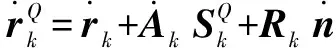
(5)
轴承与轴在碰撞时产生的接触变形,即嵌入量可表示为
=-
(6)
式中:为偏心距;为间隙大小。
嵌入量能够反映轴承与轴之间是否接触,当≤0时,轴承内圈与轴之间不发生接触,此时接触力=0;当>0时,轴承内圈与轴之间发生接触,接触区域会产生力的作用。因此,发生接触的边界条件和接触点的速度矢量可表示为

(7)
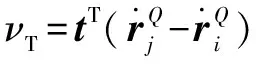
(8)
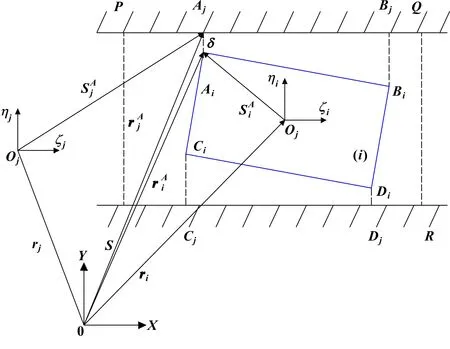
图2 移动副间隙模型
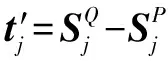
(9)
构件上任意一点的位置向量为
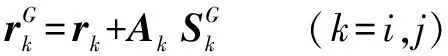
(10)
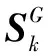
接触点位置向量和嵌入量可表示为
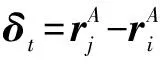
(11)
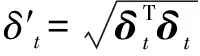
(12)
其接触碰撞速度可写成:
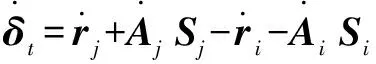
(13)
1.2 运动副间隙接触碰撞模型
接触碰撞力建模是含间隙机构动力学分析必要研究内容之一。基于非线性接触碰撞理论,并考虑阻尼因素对能力损失的影响,建立含间隙运动副的接触碰撞力模型,其表达式为
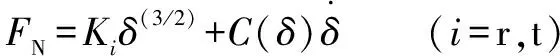
(14)

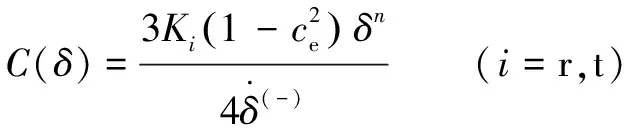
(15)

转动副间隙刚度系数可表示为
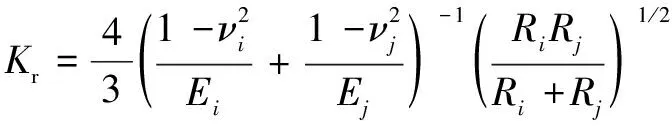
(16)
式中:为泊松比;为接触体弹性模量;为轴与轴承半径。
移动副刚度系数如下:

(17)
式中:为材料特性;为接触区域面积;和分别为滑块的长度和宽度。
摩擦力是含间隙运动副接触碰撞过程重要的参数,可描述接触特性的切向力特征,文中考虑运动副间隙为干摩擦状态。Coulomb摩擦模型可以有效描述冲击状态下非线性接触碰撞过程中的摩擦特性。为了更加准确地描述轴与轴承接触碰撞过程中的黏滞微滑现象,采用Coulomb修正模型对其进行描述,该模型中的动态摩擦因数可表示摩擦力与切向滑动之间的关系。考虑轴与轴承在实际运转过程中的摩擦现象,切向摩擦力模型表达式如下:
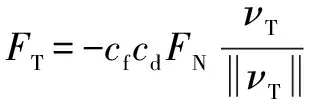
(18)
式中:表示滑动摩擦因数;为动态摩擦因数,其表达式可以写成:
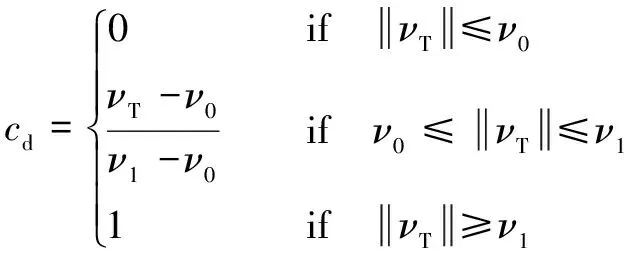
(19)
式中:和为给定的速度极限值。
1.3 含间隙碰撞的多体系统动力学方程
含间隙高速精密机构运动过程中,含间隙运动副之间会产生“自由运动”和“接触碰撞”状态,两者有可能交替发生,需要针对不同运动状态建立含间隙多体系统动力学方程。根据拉格朗日乘子法,自由状态下含间隙多体系统动力学方程为
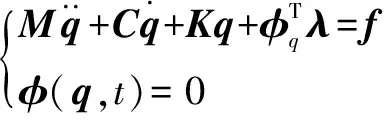
(20)
式中:、和分别为系统的广义质量矩阵、阻尼矩阵和刚度矩阵;表示广义坐标矩阵;为广义约束方程(,)=0的雅克比矩阵;和分别表示广义力阵和Lagrange乘子列阵。
当系统运动状态为 “接触碰撞”条件时,需要将接触碰撞力引入到动力学方程中来描述碰撞体之间的相互作用,其表达式为
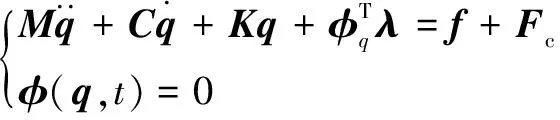
(21)
式中:为接触力相对于广义坐标的广义力列阵。
=+
(22)
2 试验验证与分析
2.1 模型参数与计算流程
高速精密机构模型如图3所示,由曲柄、连杆、滑块以及导轨几个部分组成。该机构包括两个理想转动副,分别位于曲柄与支座连接处、曲柄与连杆连接处。连杆与滑块连接处有转动副间隙,滑块与导轨之间存在移动副间隙,其机构的结构参数和材料参数如表1所示。基于上述模型,以含混合间隙高速精密机构为研究对象,通过对轴与轴承、滑块与导轨接触监测,获得含混合间隙运动副的接触碰撞力。基于Runge-Kutta法对系统动力学方程进行迭代求解,完整计算流程如图4所示。
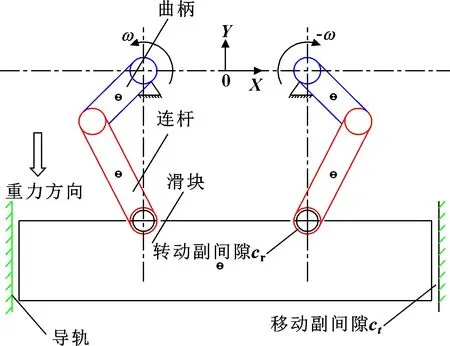
图3 仿真计算模型
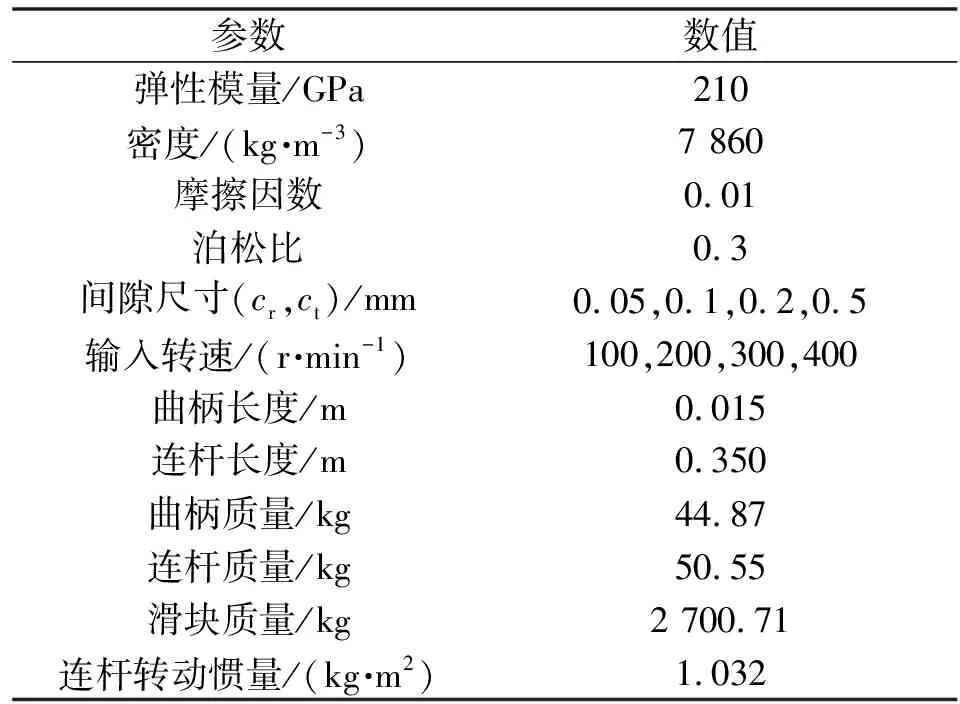
表1 模型基本参数
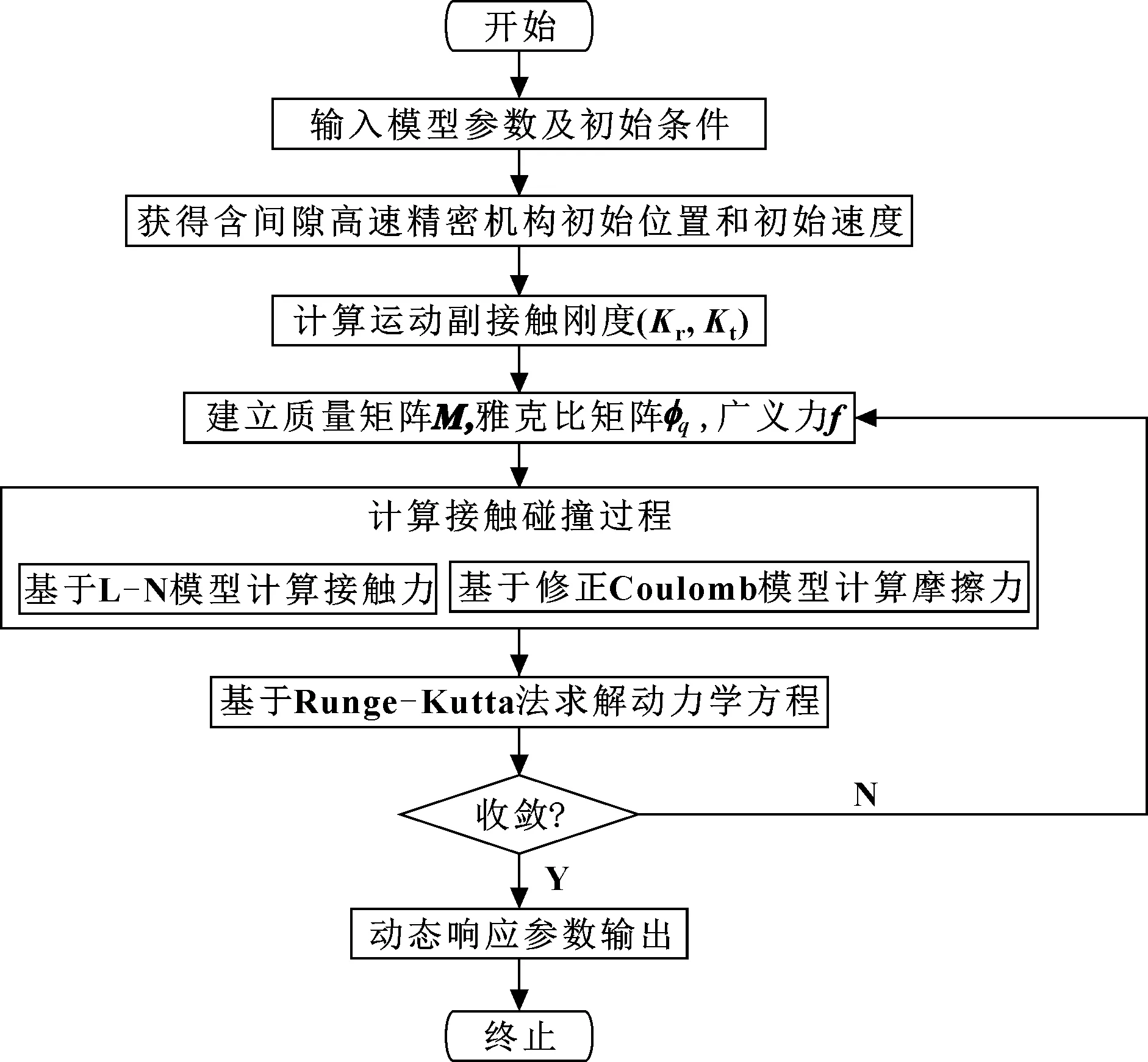
图4 计算流程
2.2 试验分析
针对含混合间隙高速精密机机构动态特性分析,在高速精密机械压力机试验平台上进行了性能试验,对滑块动态性能进行了测试。试验装置由机械部分和测试系统两部分组成,机械部分由电机、驱动轮、飞轮、离合器、曲轴、连杆、滑块七部分组成;测试系统由无线加速度传感器、无线接收器和数据采集分析系统组成。无线加速度传感器安装在滑块上,用于测量滑块垂直方向的加速度。数据采集分析系统运行在必创操作平台上,集信号采集、滤波、A/D转换和数据分析于一体。该测试系统可以测量滑块运动时任意时刻加速度值。为了保证测量精确度,试验前对加速度传感器进行了专门标定。机构动态性能实验测试图如图5所示。
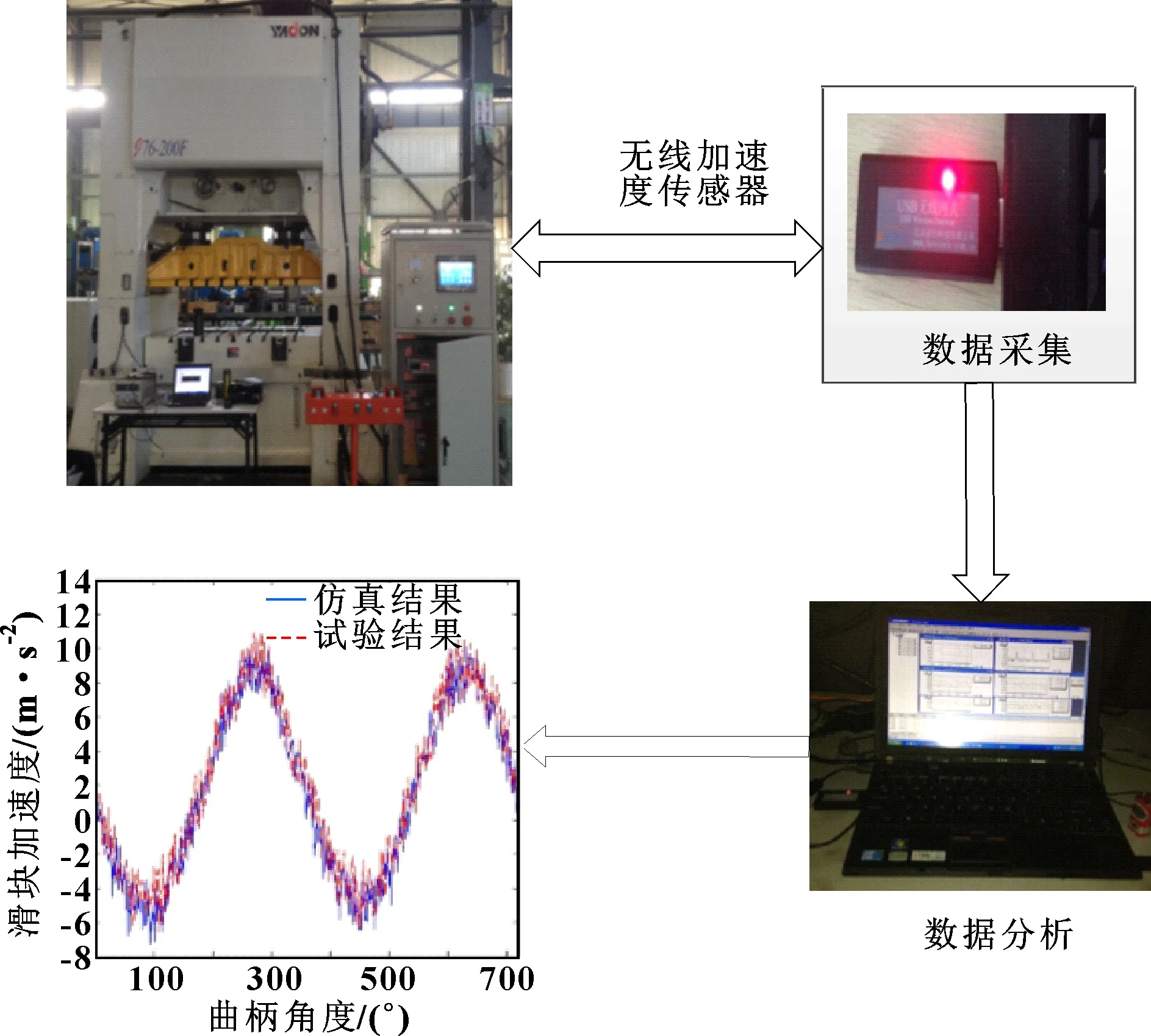
图5 机构动态性能试验测试图
不同转速下高速精密压力机滑块加速度的仿真结果与测试结果对比如图6所示。可知:含间隙运动副元素之间呈现不同的状态。在高速精密机构运转过程中,含间隙运动副引起高速精密机构发生振动,滑块加速度产生峰值波动和非线性增长现象。在滑块位于下死点位置时,接触力会出现高频振动,此时含间隙运动副发生在接触变形现象;而对于整个运动周期而言,连续接触状态占据时间最长。滑块加速度仿真计算结果与测试结果极其相似,从而验证了文中建模方法的有效性。
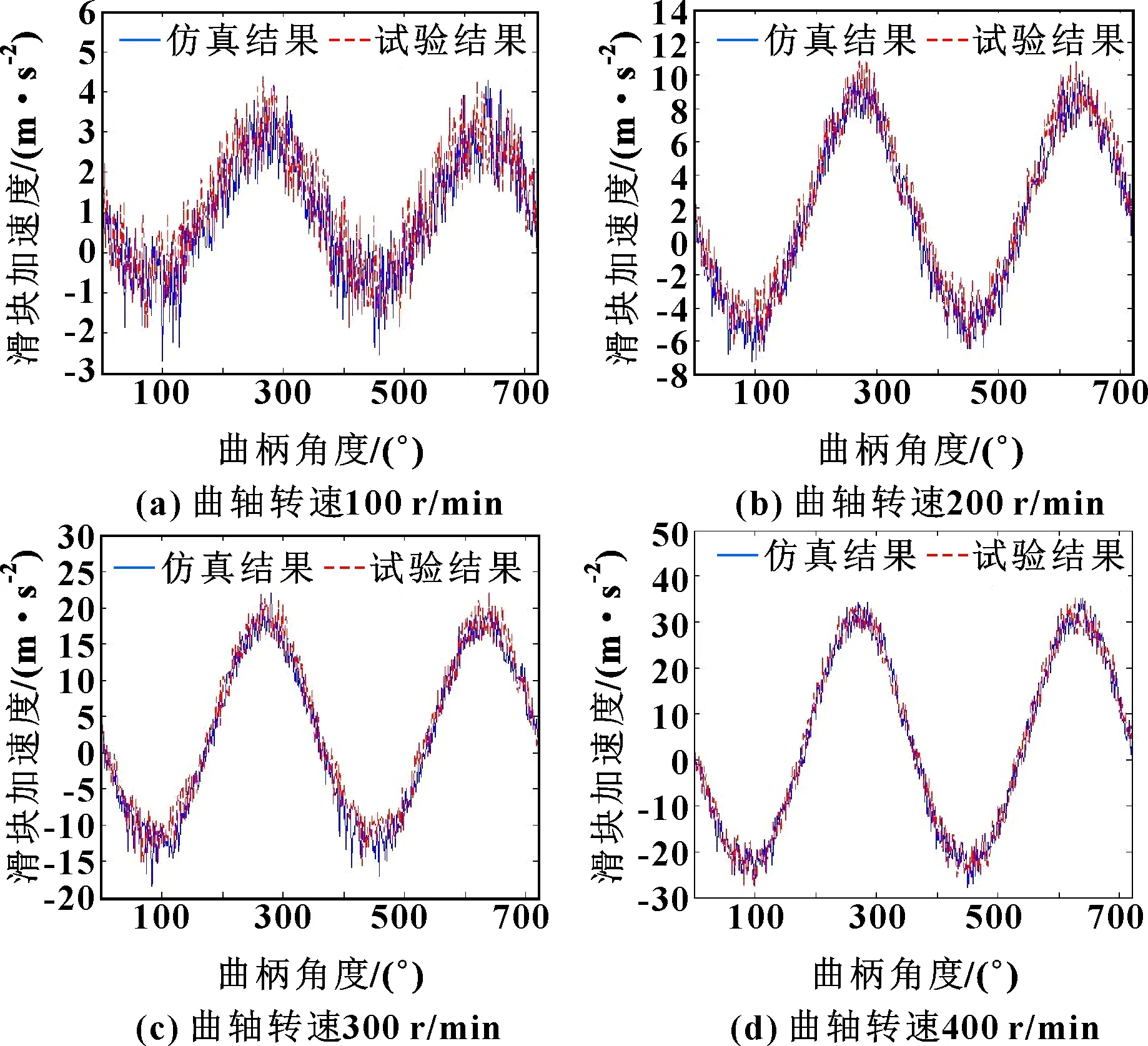
图6 测试曲线与仿真曲线对比
3 数值分析
为了对混合间隙影响下高速精密机构非线性动态响应问题进行更为深入的研究,对不同输入转速和间隙尺寸条件下高速精密机构动态特性进行多体动力学仿真,获得其机构非线性动力学行为以及混沌运动响应特征。
3.1 输入转速影响分析
采用文中所述的建模方法,建立不同参数下高速精密机构的动力学仿真模型,研究运动副间隙对离散状态高速精密机构动力学行为的影响。当运动副间隙为0.1 mm时,分别获得输入转速为100、200、300、400 r/min时轴心轨迹如图7所示。可知:在高速精密机构运动过程中,运动副单元出现3种不同的运动状态,包括自由状态、连续接触状态、接触碰撞状态;连续接触状态占比较大,在较低转速时,高速精密机构动态响应趋于非线性特征;随着输入转速的增加,接触碰撞状态明显增强,其嵌入深度明显增加。
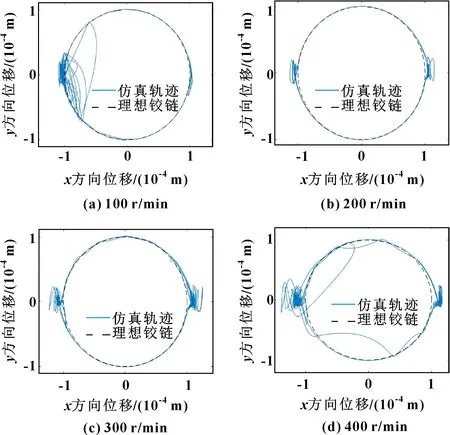
图7 输入转速对轴心轨迹的影响间隙(c=0.1 mm)
图8和图9显示了在不同输入转速下高速精密机构非线性动态响应特征,计算结果描述了滑块运动的相位关系以及机械系统的运动状态。由计算结果可以看出滑块运动轨迹由左、右两簇构成,各自围绕一点运动,在输入转速较低时该特征表现得更加明显,出现非周期性混沌现象。随着输入转速的增加,运动轨迹向边缘靠近,运动轨迹轮廓逐渐清晰,呈现出倍化分岔序列。同时,Poincaré图中表示出相对应的变化趋势,随着输入转速的增加,吸引子的形状结构趋于稳定,吸引子的集中区域变大。
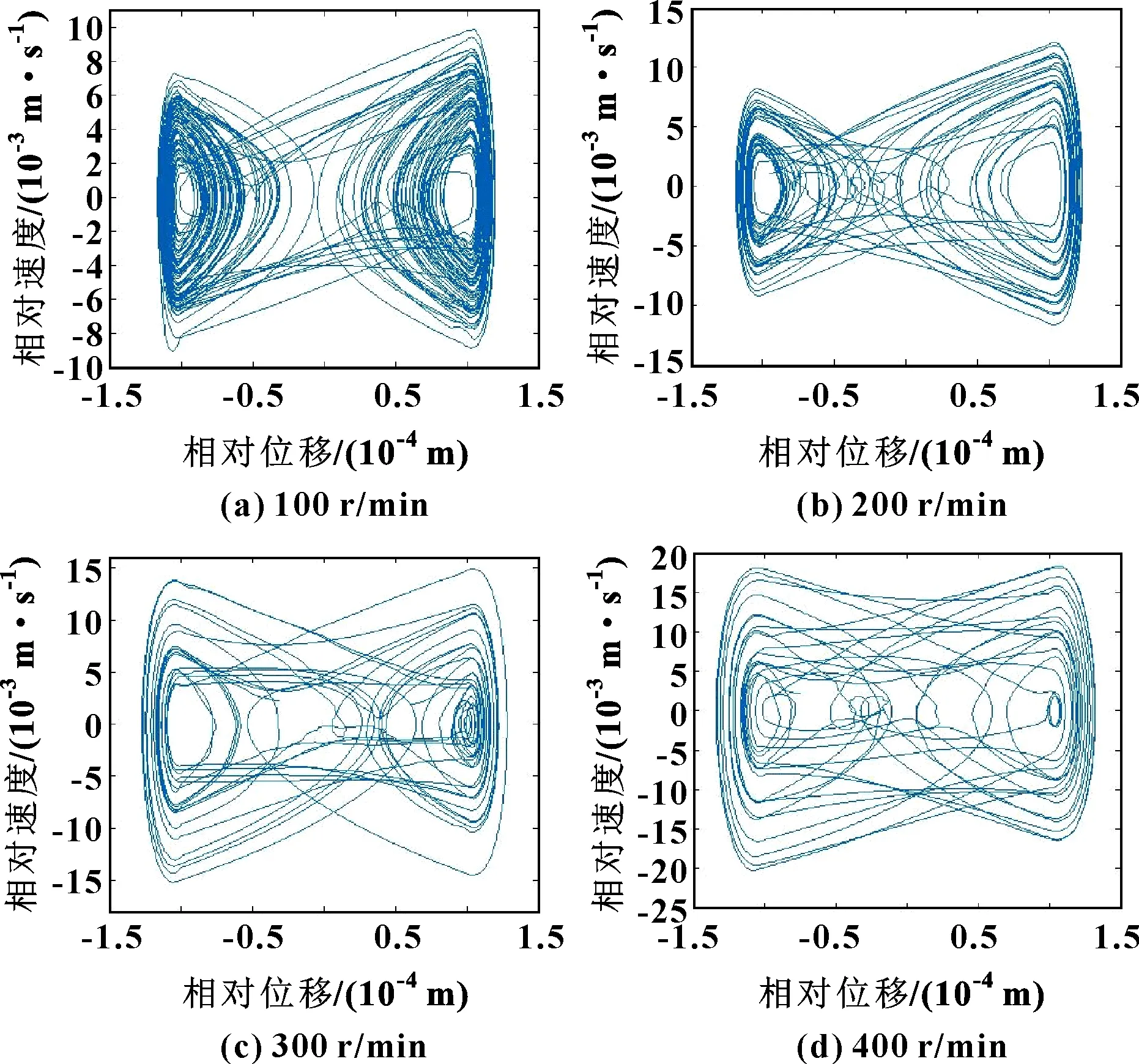
图8 输入转速对运动副相对运动的影响(c=0.1 mm)
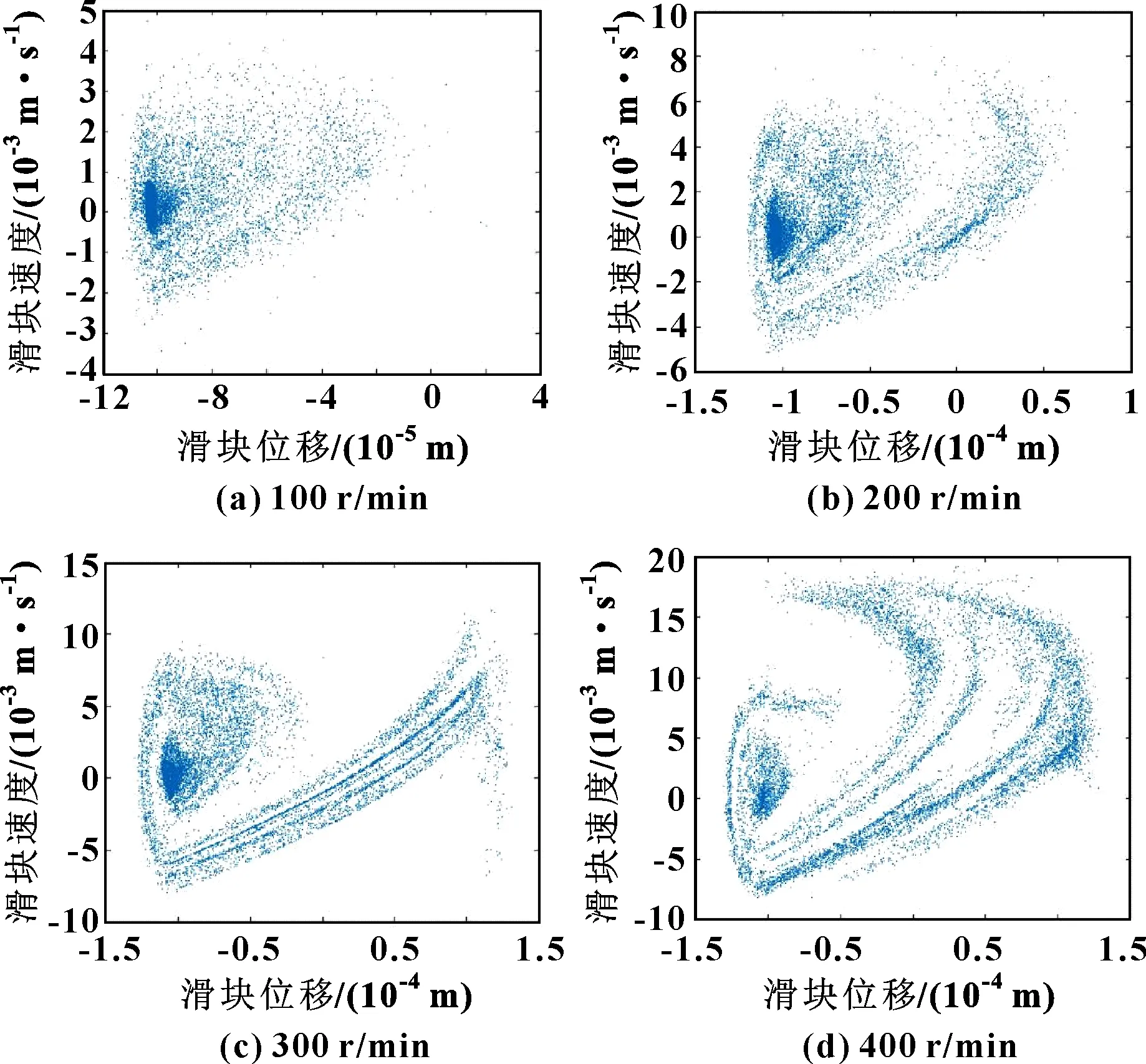
图9 输入转速对滑块运动轨迹的影响(c=0.1 mm)
3.2 间隙尺寸影响分析
间隙尺寸是影响含间隙高速精密机构动力学性能的主要因素之一。为了更加详细地分析含间隙高速精密机构非线性动态响应特征,建立不同间隙尺寸的高速精密机构动力学分析模型。计算模型中,输入转速为200 r/min,间隙尺寸分别为0.05、0.1、0.2、0.5 mm。轴心运动轨迹可以表示出含间隙运动副元素之间的运动状态,研究间隙对轴心轨迹的影响对于含间隙高速精密机构设计具有重要意义。间隙尺寸对轴心轨迹影响如图10所示,不同间隙尺寸下轴心轨迹分布情况各不相同。当间隙值较小时,轴心轨迹分布在轴承边缘区域,主要为连续接触状态和接触变形状态;随着间隙尺寸的增加,轴心运动轨迹范围增大,运动副元素自由运动空间增大。同时,较大的间隙尺寸会使运动副元素获得更多的能量,加大碰撞过程中的冲击力,嵌入深度也随之增加。
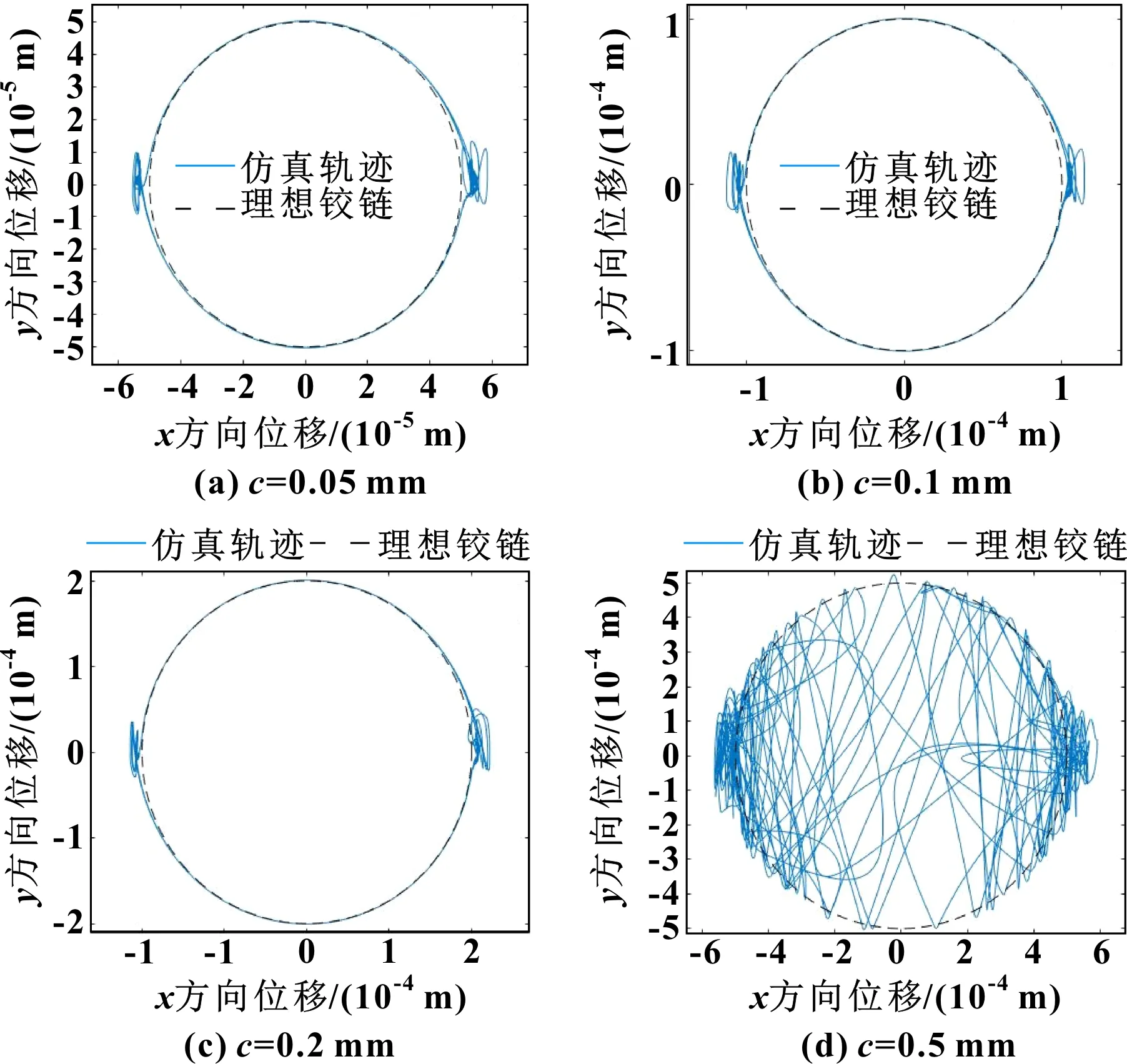
图10 间隙尺寸对轴心轨迹的影响(输入转速200 r/min)
由于间隙的存在,高速精密机构的间隙铰链在运动过程中会产生滑动和碰撞现象,运动副元素会在不同运动状态下来回切换,间隙对运动副相对运动影响如图11所示。可知:高速精密机构动力学行为对间隙尺寸的变化较为敏感。当间隙尺寸较小时,轨迹在左侧位置较为集中,当接近于中心位置点时会瞬间跳转到右侧边缘位置,并逐渐再次向中心位置靠近,反复盘旋运动;随着间隙尺寸的增大,运动轨迹向边缘位置靠近,这说明高速精密机构运动周期性发生变化。图12描述了不同间隙尺寸下高速精密机构吸引子的变化趋势。间隙尺寸的增加引起接触碰撞力的增大,从而使得吸引子集中区域发生改变,机械系统产生混沌和分岔现象。
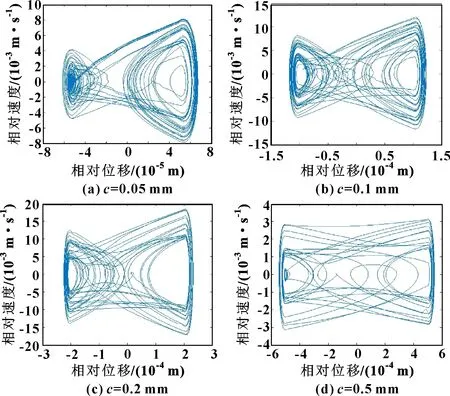
图11 间隙尺寸对运动副相对运动的影响(输入转速200 r/min)
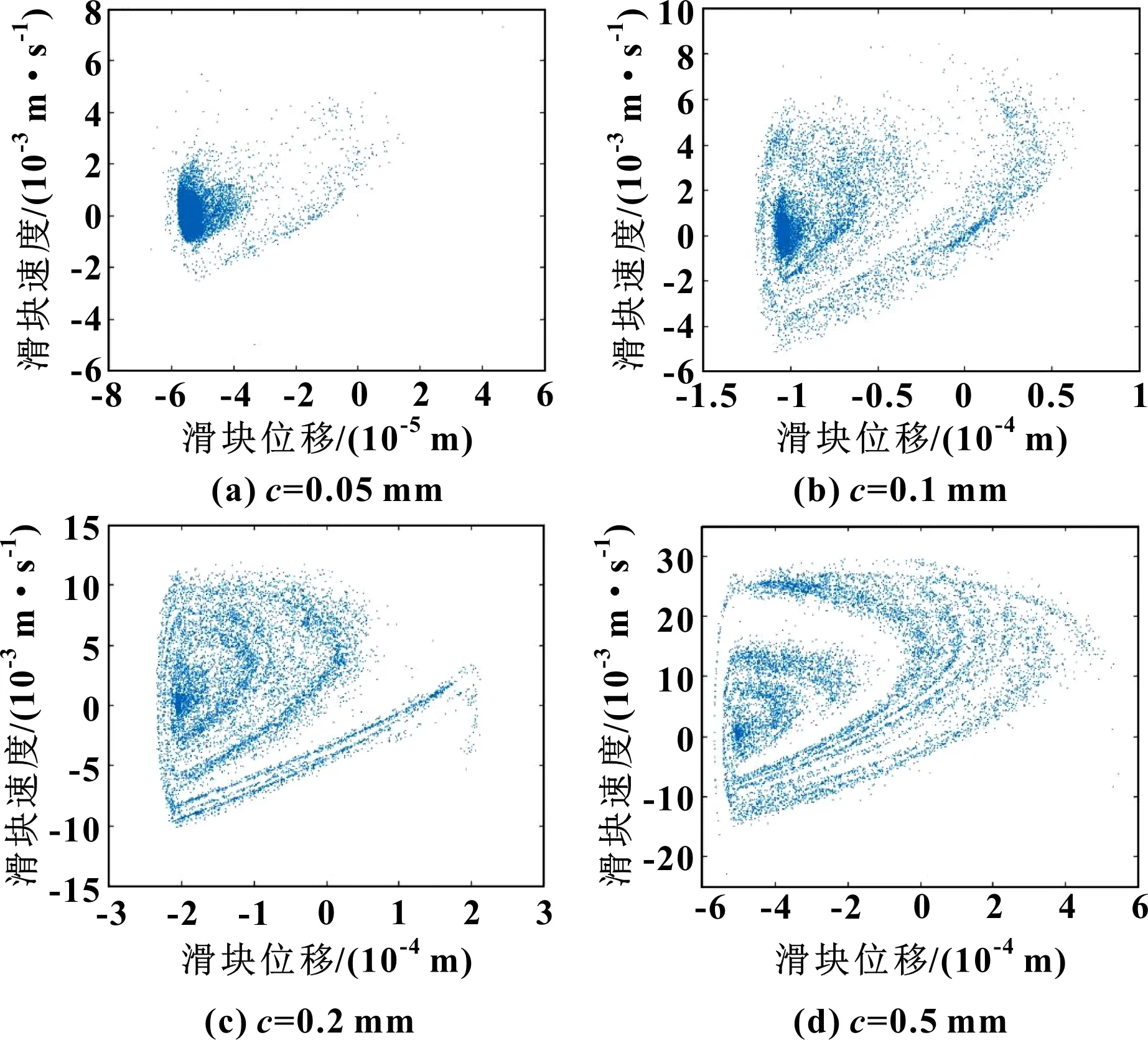
图12 间隙尺寸对滑块运动轨迹的影响(输入转速200 r/min)
4 结论
基于多体动力学理论和非线性接触碰撞理论,提出一种含混合间隙的高速精密机构动态特征分析的建模方法,根据L-N接触力模型获得运动副元素之间的接触碰撞力,并采用Runge-Kutta对系统动力学方程进行求解,研究了高速精密机构混沌与分岔特性。主要结论如下:
(1)由于间隙的存在,运动副元素之间存在自由运动、连续接触和接触变形状态,在高速精密机构运动过程中,运动副元素在不同状态下来回切换,并伴随较大的振动与冲击。
(2)高速精密机构在输入转速和间隙尺寸等因素影响下,呈现出明显的分岔和跳跃特性,随运动参数的变化出现了倍周期、多周期和混沌等运动状态。
(3)输入转速、间隙尺寸过大或过小都会引起运动副元素之间的激烈运动,产生强烈的碰撞,机械系统通过激变进入混沌运动状态。文中所提建模方法更加真实地描述了多体系统非线性动态响应特性,为机构的性能评价、结构优化设计等奠定了基础。
