最小非线性插补误差约束的多轴侧铣刀轴矢量优化

2022-09-19赵恒万能张森堂高石印

机床与液压 2022年8期

赵恒，万能，张森堂，高石印

(1.中国航发沈阳黎明航空发动机有限责任公司，辽宁沈阳 110043；2.西北工业大学工业工程与智能制造工信部重点实验室，陕西西安 710072)

0 前言

航空发动机中承载能量传递的关键零件侧铣相比点铣具有取材效率高、刀具损耗小的优点，因此在航空制造领域有大量研究聚焦于侧铣工艺。

目前，许多研究者对保证侧铣精度进行了广泛研究，优化加工路径是其中的讨论热点。但是，这些研究往往是在工艺编制的设计坐标系中进行计算与优化。如果将切削路径转化到机床坐标系中，机床运动轴的插补运动会引入额外的误差。在五轴加工线性插补中，存在着刀具位置的直线逼近误差和刀轴摆动的误差。由于刀具位置的误差直接影响加工精度，研究人员对刀具位置在插补中的非线性进行了大量研究，通过补偿等方法基本解决了刀具位置在插补中非线性运动的问题。刀轴摆动的误差不影响刀轴位置，因此优化刀轴的目的是使刀轴矢量更平滑，从而保证加工质量。樊留群等指出在通过平动轴补偿刀具位置的非线性运动后，机床转动轴仍然会默认以线性插补方式进给，造成了刀轴矢量偏离理想的线性插补，在铣削腔体内斜面时造成较大误差。杨旭静等分析了刀轴矢量在插补中的非线性运动对侧铣和点铣加工误差的影响，给出了插补中刀轴最大偏差角的近似表达式，提出了通过限制相邻刀轴矢量夹角的方法来减少刀轴最大偏差角。周玉龙针对旋转轴运动引起的非线性误差，通过一次试探法约束转轴进给速度以补偿非线性误差。高超峰对侧铣加工曲面表面微结构进行了研究，规划了应用于多齿鼓形刀的侧铣加工路径。肖海涛提出一种约束预插补和S形速度规划的算法,保证了非线性误差不超限以及速度、加速度的平滑变化。

本文作者分析刀轴矢量非线性插补的成因，甄别出影响因素，提出减小刀轴矢量非线性插补误差的方法。

1 线性插补中刀轴矢量的非线性插补

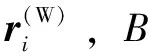
图1 BC轴机床坐标系关系

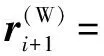
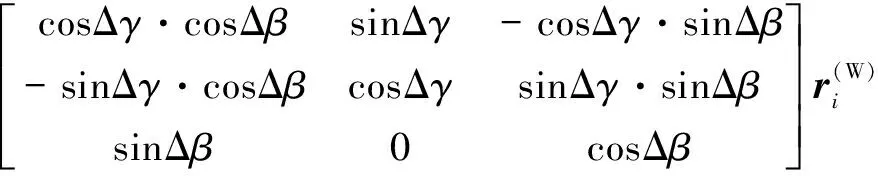
(1)

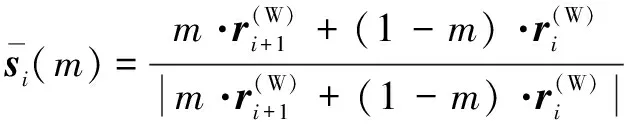
(2)

实际机床是旋转轴做线性插补运动，则在时刻，加工坐标系中实际刀轴矢量()为

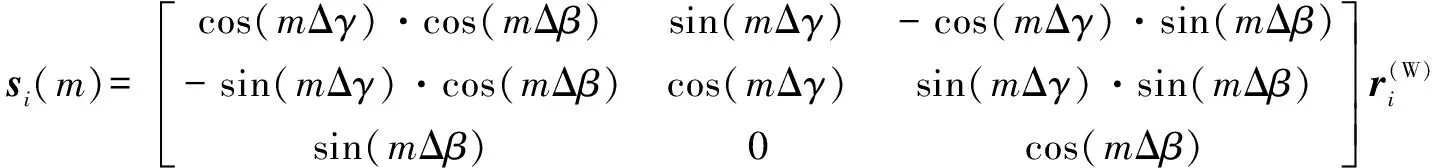
(3)

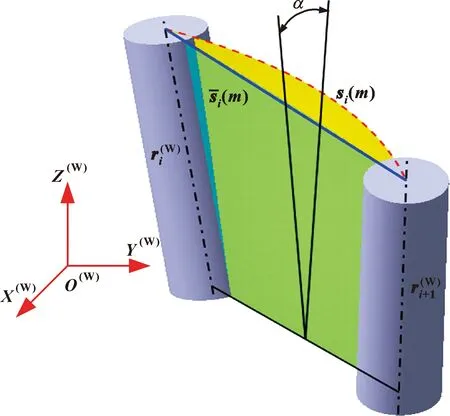
图2 刀轴矢量非线性插补

刀轴偏差角越大，造成的切削误差越大。假设侧铣的有效刃长为，一次插补运动中刀轴偏差角最大值为，则插补中造成的切削误差最大值为

=·tan

(4)

对于侧铣，由于侧刃的有效刃长较大，刀轴矢量非线性插补引起的加工误差可能严重影响加工精度。

2 刀轴矢量的插补形式与条件

2.1 刀轴矢量非线性插补的条件

如图3所示，在加工坐标系中将相邻刀轴矢量刀心点平移至原点，构建单位球面坐标系。在加工坐标系中，刀轴矢量插补时在单位球面上扫掠出轨迹()。基于该球面上刀轴矢量的扫掠轨迹，本文作者提出两个定理：

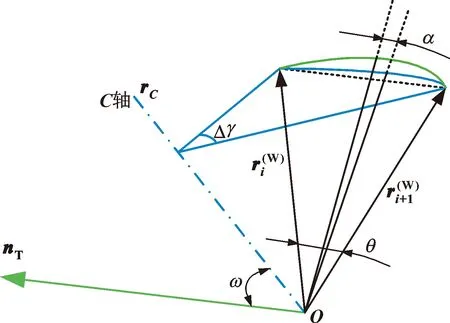
图3 单个转轴转动的刀轴矢量变化轨迹

定理1：如果刀轴矢量做线性插补运动，则刀轴矢量在球面的变化轨迹()是测地线。

定理2：在机床旋转轴线性联动的条件下，刀轴矢量在球面的变化轨迹()不是圆弧。

2.2 刀轴矢量线性插补条件

根据刀轴矢量的球面轨迹，分析机床仅有一个旋转轴转动的条件下，刀轴矢量线性插补的条件。

若Δ=0或Δ=0，机床仅有一个转轴旋转运动，此时刀轴矢量在球面的变化轨迹是圆弧，但该圆弧不一定以球心为圆心。

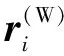
(5)

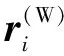
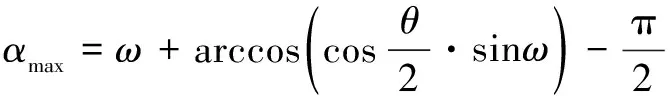
(6)

为0时，()为测地线，最大的刀轴偏差角为0。当为π/2时，上界为2。给出刀轴矢量线性插补条件的定理：

定理3：机床仅有单个旋转轴转动，且旋转轴与插补始末的刀轴矢量垂直时，刀轴矢量在球面的变化轨迹()是测地线。

3 刀轴偏差角的计算

通常认为，单次插补运动中机床旋转轴线性进给，所以刀轴偏差角可以通过球面轨迹的矢量积求得：

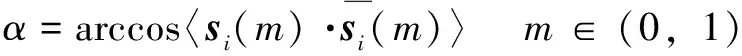
(7)

通常关注的是插补过程中最大的偏差角，设参数使得取得最大值，则有：

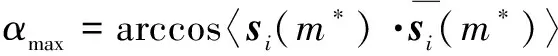
(8)

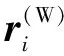
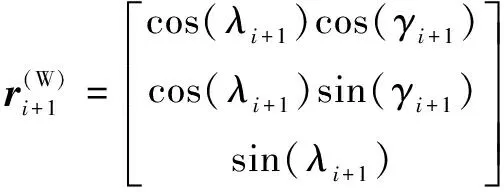
(9)

()=

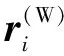
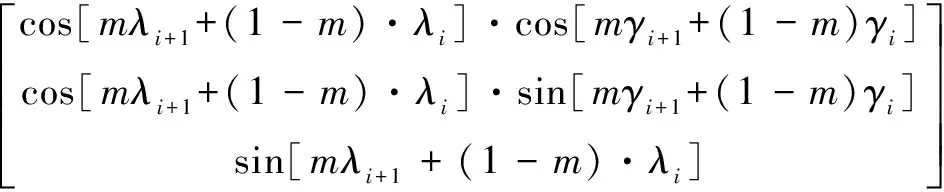
(10)

计算偏差角的余弦：

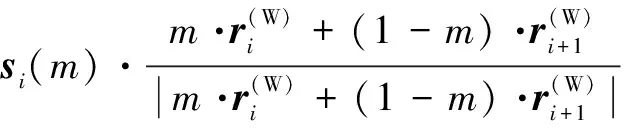
(11)

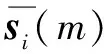
()={(1-)++(2-2)·[sin(-)·sin(+)+cos(-)·cos(+)·cos2]}12

(12)

()=sin(-+2)·[·sin(+)+

(1-)·sin(-)]·(1-)·cos(-)·cos(2)]·(1-)·cos(-)·cos(2)]

(13)

式中：为起止刀轴矢量的平均纬度;为单次插补中机床轴转角的12(纬度差的12);为机床轴转角的1/2(经度差的1/2)。可以看出,刀轴偏差角与刀轴矢量在球面坐标系中的经度位置无关,而与经度差、纬度差及纬度位置有关。

为分析插补中刀轴的最大偏差角与参数、、的关系，构造最大偏差角的余弦函数(,,)=cos，则(,,)的表达式为

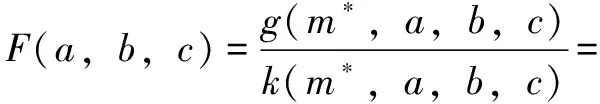
(14)

不同的相邻刀轴矢量对应不同的经纬度参数、、，因此单次插补运动中对应最大偏差角的插补参数不同。在球面坐标系中确定了刀轴矢量的参数、、后，需要以数值方法计算最大误差处的插补参数，再计算(,,)，确定插补中刀轴矢量的最大偏差角。

4 刀轴矢量非线性插补误差的优化

4.1 刀轴最大偏差角的近似

为减小刀轴矢量非线性插补造成的误差，文献[10]的思路是限制相邻刀轴矢量的夹角。针对限制相邻刀位点处刀轴矢量的夹角的观点，文中给定夹角条件下可能的参数、、的组合求解，计算(,,)。考虑到相邻刀轴矢量的夹角不会过大，仅计算从1°～45°的情况，的离散精度为0.05°。计算在给定刀轴矢量夹角条件下，最大偏差角余弦的下限，结果如图4所示。

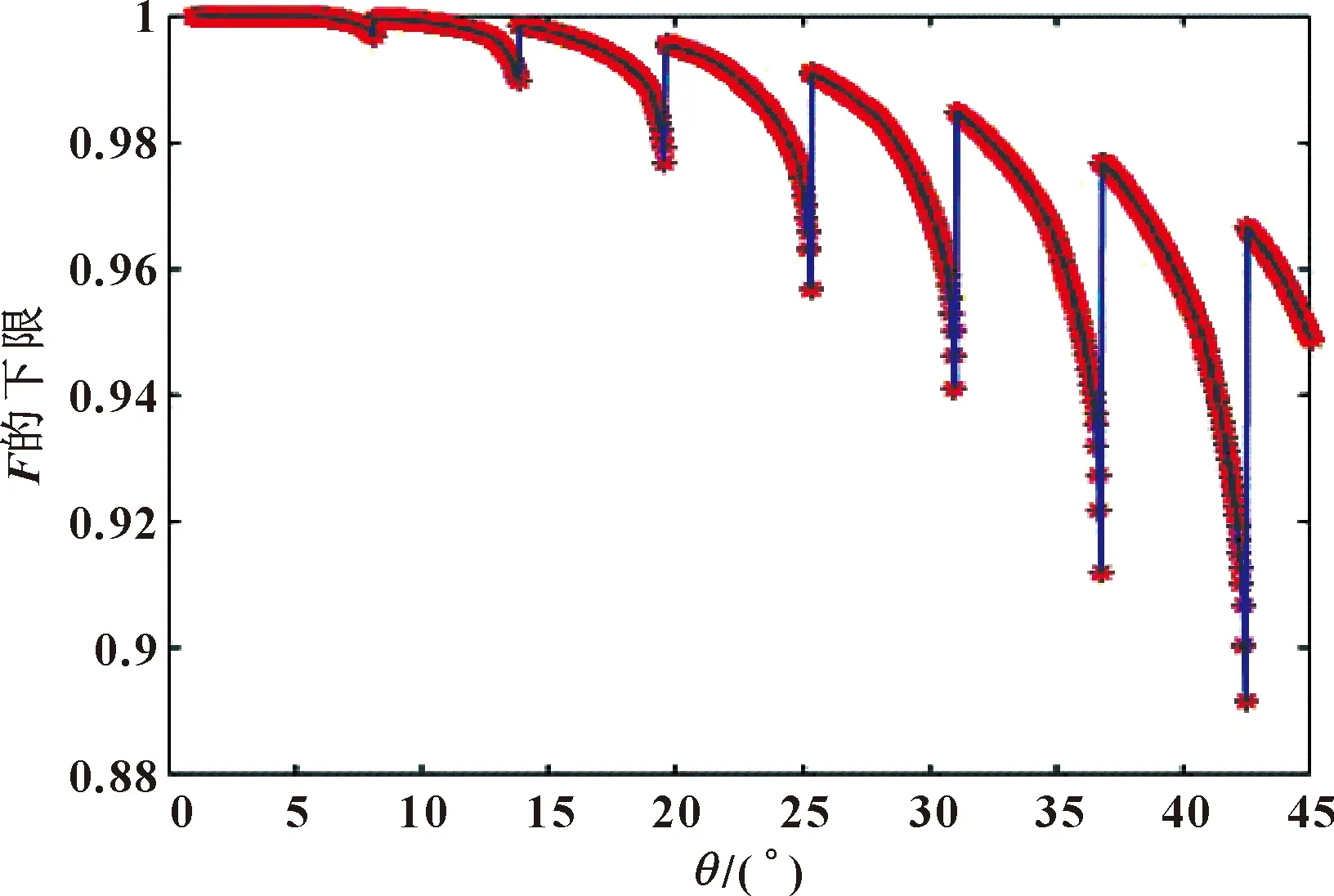
图4 最大偏差角余弦值的下限

图中纵坐标为最大偏差角的余弦值在刀轴矢量夹角为定值的条件下，可能达到的下限。可以看出，余弦的下限并不是随着刀轴矢量夹角的增加而单调减少的。因此,减少刀轴矢量的夹角既不能保证一定减少刀轴最大偏差角，也不能保证减少最大偏差角余弦值的下限。

为避免频繁求解插补参数，对式(15)进行近似处理。

(15)

从数值计算的角度分析，因为插补的初始和终止时刻刀轴矢量与理想状态重合，偏差角为0，所以有(0)(0)=1、(1)(1)=1。根据数值微分公式估算函数()()在插补中间时刻的导数值。

忽略高阶导数得：

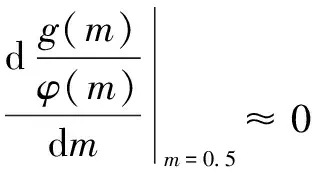
(16)

因此,偏差角余弦的极值可以认为在插补的中间时刻达到，所以插补运动中最大偏差角的余弦值可以估算为

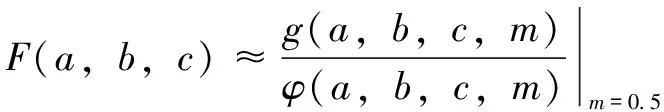
(17)

根据式(16)在给定刀轴矢量夹角条件下，计算(,,)的下限，与式(13)的结果进行比较，结果如图5所示。

图5 F下限的估算值与实际值

实际计算中发现，当平均纬度小于2时，精确的的变化幅度较大，一般在0.5～0.78之间(但此时最大偏差角余弦约等于1，非线性运动造成的偏差角可以忽略)；当平均纬度大于2时，取值接近于0.5。因此,以插补参数=0.5处的值代替准确的，该近似插补参数的误差是可以接受的。以=0.5时的偏差角代替插补过程中的最大偏差角，达到了化隐格式为显格式的目的。

4.2 优化方程的建立

文中的优化思路是在不改变设计坐标系中刀轴位置方向的前提下，对设计坐标系DCS和加工坐标系WCS的相对姿态进行调整，达到优化非线性误差的目的,使考虑了刀轴矢量非线性插补的加工效果，更贴近不考虑刀轴矢量非线性插补的理论加工效果。

如图6所示，若将设计坐标DCS相对加工坐标系WCS进行旋转变换，令设计坐标系与加工坐标系方向不再一致，相对加工坐标系变换的刀位点和刀轴矢量集合称为优化后的加工路径。可以看出,旋转前后的相邻刀轴矢量夹角不变，但是它在加工坐标系的坐标发生变化，经纬度参数、、也发生改变。下面分析给定夹角条件下，相邻刀轴矢量的经纬度参数关系。

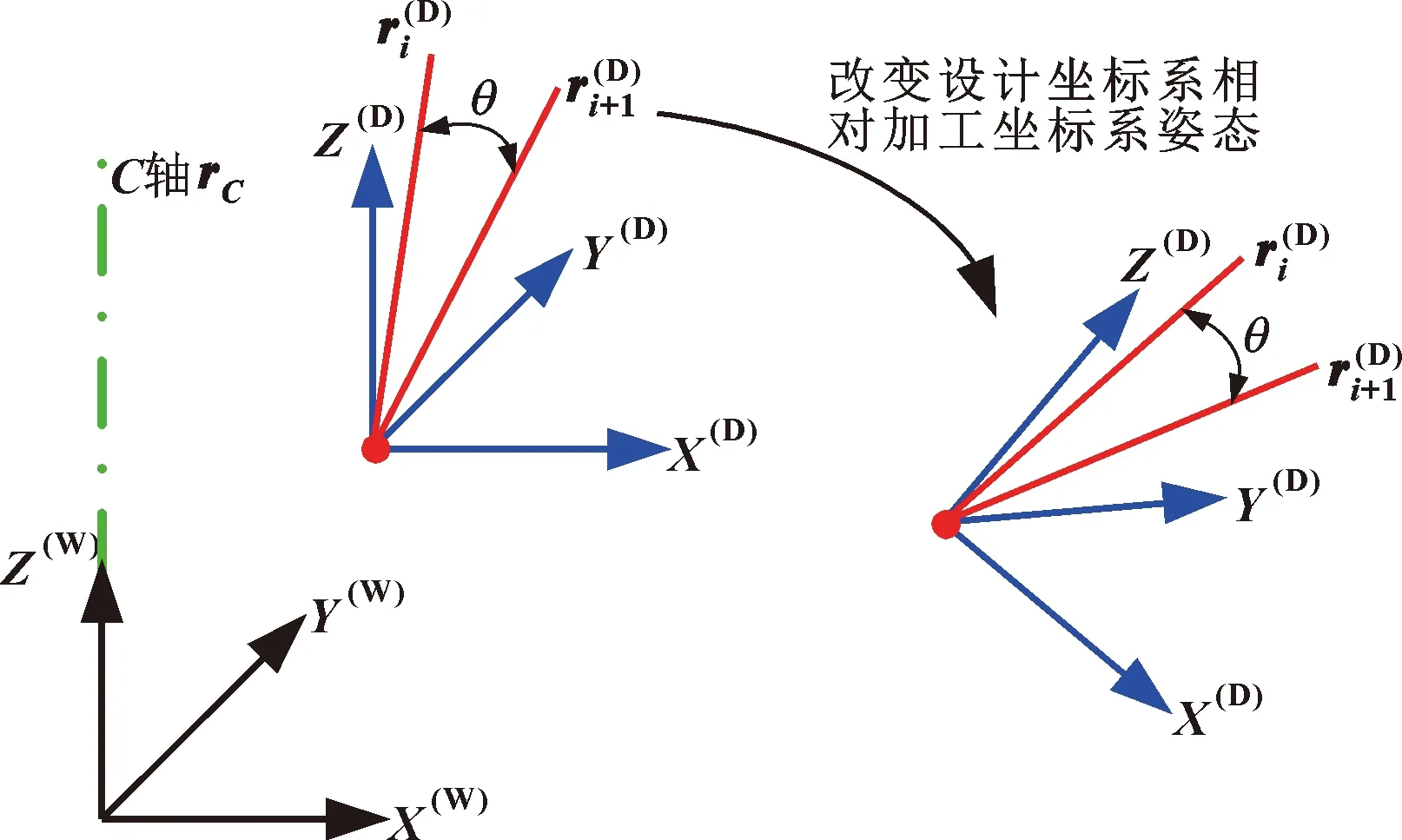
图6 旋转设计坐标系相对加工坐标系的方向

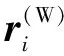
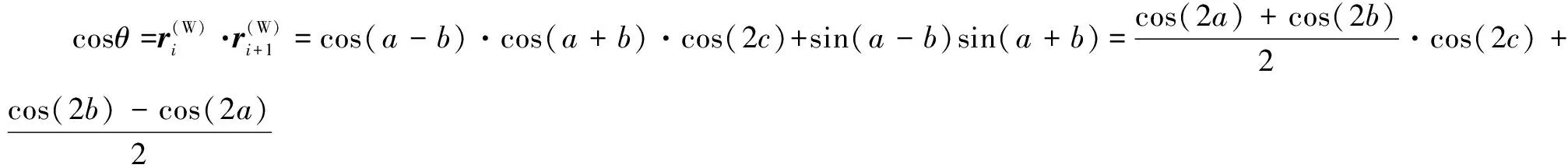
(18)

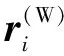
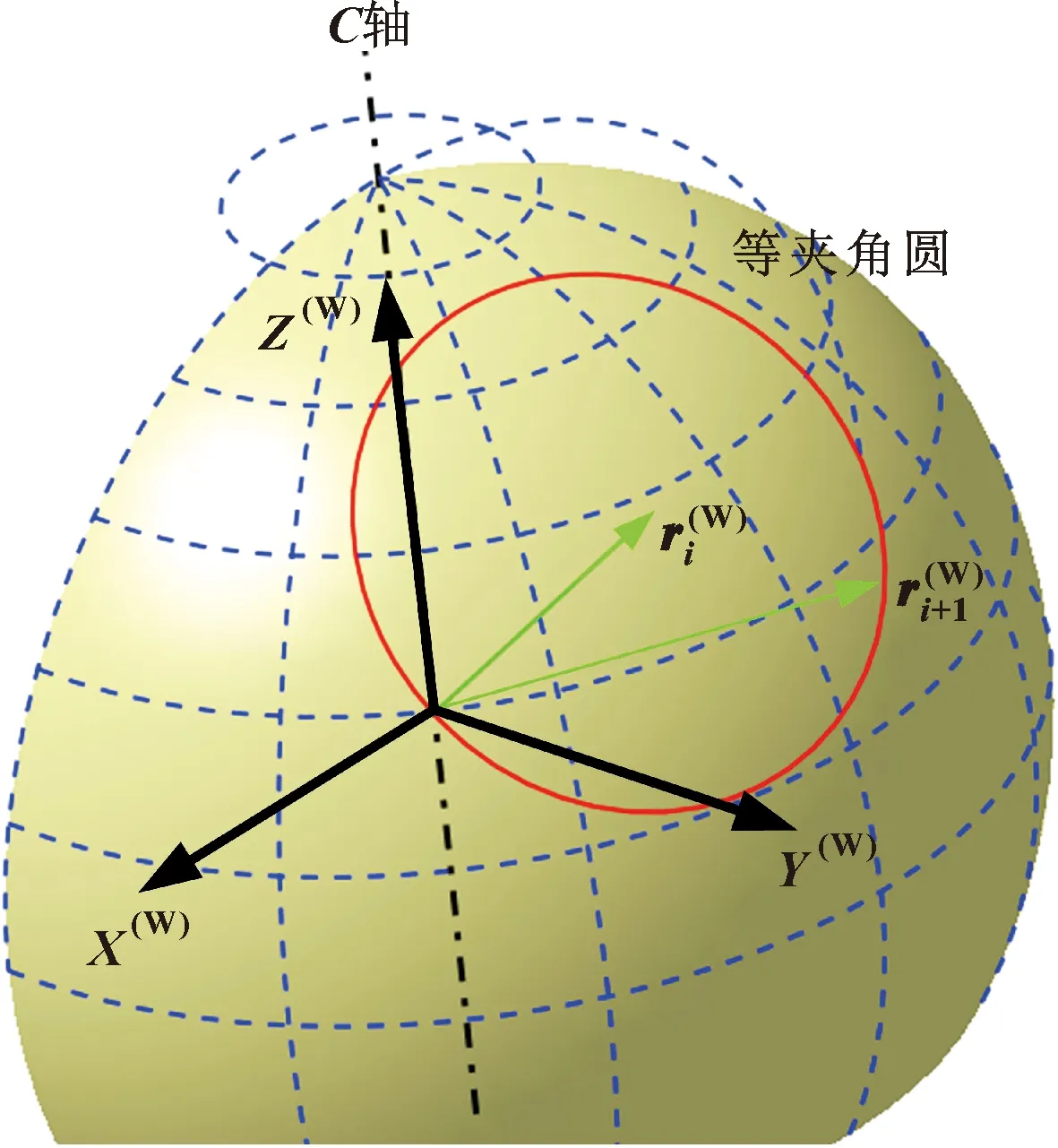
图7 刀轴矢量夹角对经纬度的限制

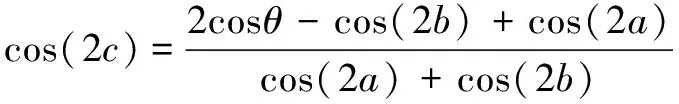
(19)

给定相邻刀轴矢量夹角的条件下，和的值域满足式(18)与(19)，因此式(18)可以化为

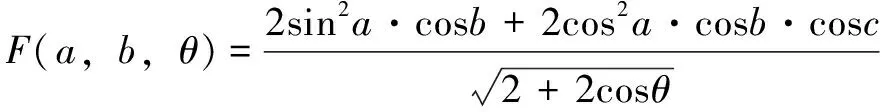
(20)

式(20)中需要满足式(19)中对夹角的要求。

将最大偏差角余弦对平均纬度求导：

(21)

式(21)的正负性难以直接判断，因此对从1°～45°的∂/∂导数进行遍历，经计算发现∂/∂的值均小于等于零。以为30°的情况为例，∂/∂的值分布如图8所示，刀轴矢量夹角为其他值时导数有类似的分布。这说明最大偏差角的余弦随着刀轴矢量平均纬度的增加而减少，即刀轴矢量的平均纬度越高，最大偏差角越大。

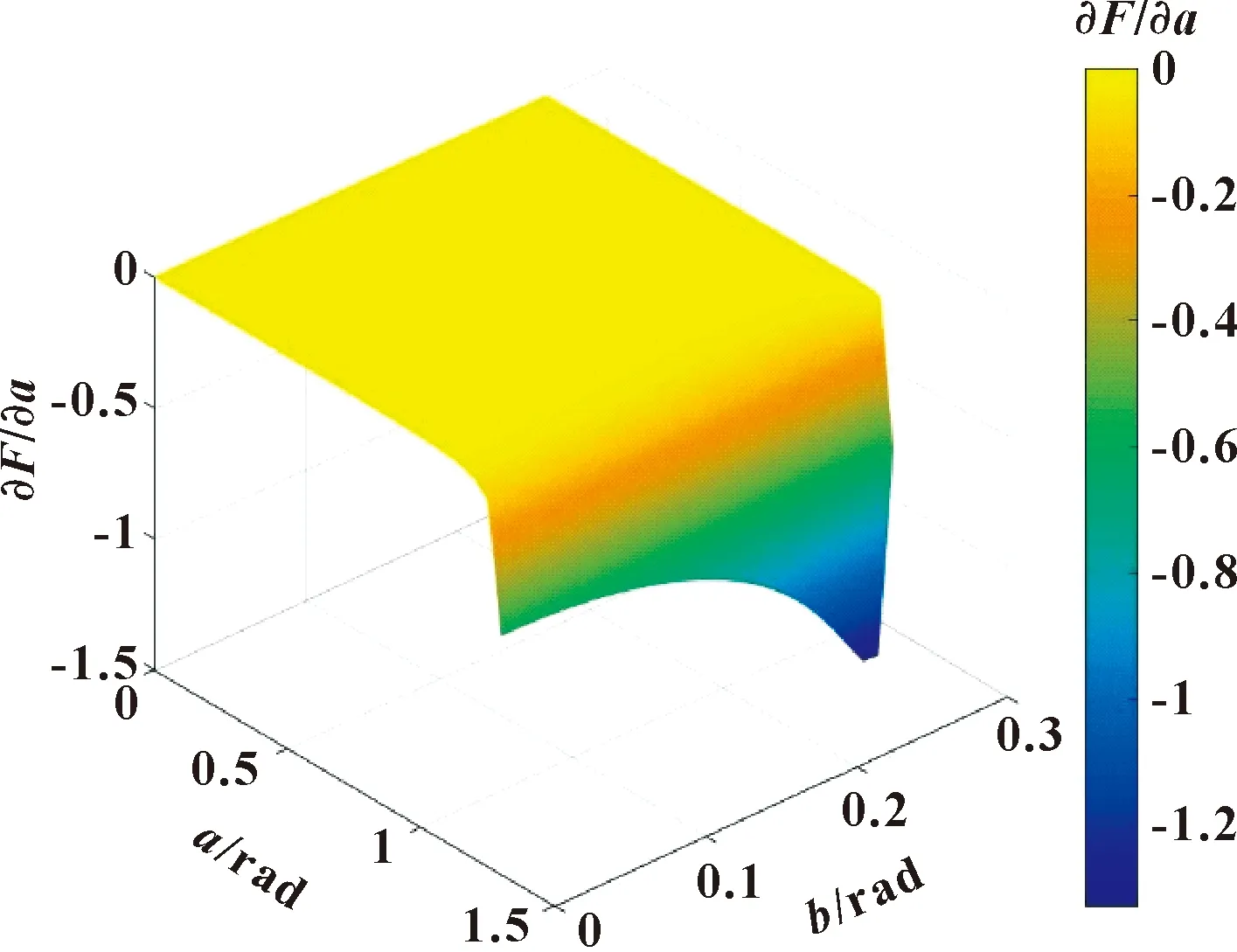
图8 最大偏差角余弦对a的导数(θ=30°)

再分析最大偏差角余弦对纬度差1/2的导数，将对求导，表达式如下：

(22)

对式(22)在定义域内进行遍历计算，当>0时，经计算发现导数大于0，因此随着纬度差的增加余弦值增加，最大偏差角减小；当<0时，导数小于0，纬度差减小(绝对值增大)，余弦值增加，最大偏差角减少。

根据上面的分析，为减少刀轴矢量非线性插补引起的误差，提出两种优化策略：(1)降低刀轴矢量的平均纬度；(2)增加刀轴矢量纬度差。同时，这两种优化策略也会导致刀轴矢量的经度差绝对值减小。

分析纬度差2和平均纬度对最大偏差角的影响，结果如图9所示。在刀轴矢量夹角为定值的条件下，计算不同平均纬度对应的最大偏差角上下限。

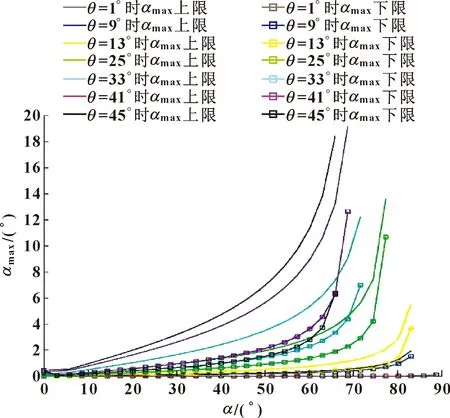
图9 不同平均纬度对应的最大偏差角的极值

从图9中可以看出：由于平均纬度的变化范围较大，在刀轴矢量夹角固定时对最大偏差角的影响比较显著；而刀轴矢量夹角通常较小，因此相邻刀轴矢量纬度差变化范围较小，最大偏差角的上下限比较接近。对侧铣刀轴矢量经纬度参数的优化，重点在于降低刀轴矢量的平均纬度。

因为轴旋转对刀轴矢量的经纬度参数没有影响，所以令优化非线性误差的旋转为设计坐标系绕加工坐标系轴和的旋转，令和分别表示绕各轴的旋转量，则刀轴矢量坐标的旋转变换矩阵为

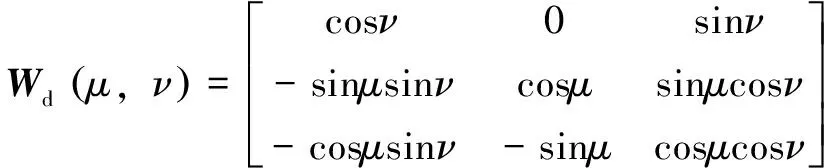
(23)

以该旋转变换矩阵作用于设计坐标系，旋转后规划的刀轴矢量在加工坐标系中的坐标为

(24)

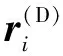
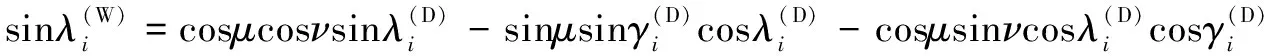
(25)

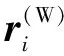
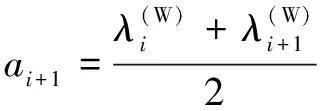
(26)

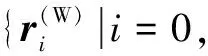
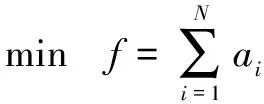
(27)

采用数值方法求出满足式(27)的旋转角度和，并做相应的姿态调制。由于该优化过程不改变设计坐标系中刀具与模型的相对位置关系，对不考虑刀轴非线性插补的理论加工误差没有影响，仅使考虑刀轴非线性插补的加工效果更加接近理想的加工效果。

5 实验

如图10所示，对一个样条自由曲面规划了两行侧铣加工路径。根据加工路径中刀轴矢量在球面坐标系的分布情况，对路径进行优化，比较优化前后的加工效果。

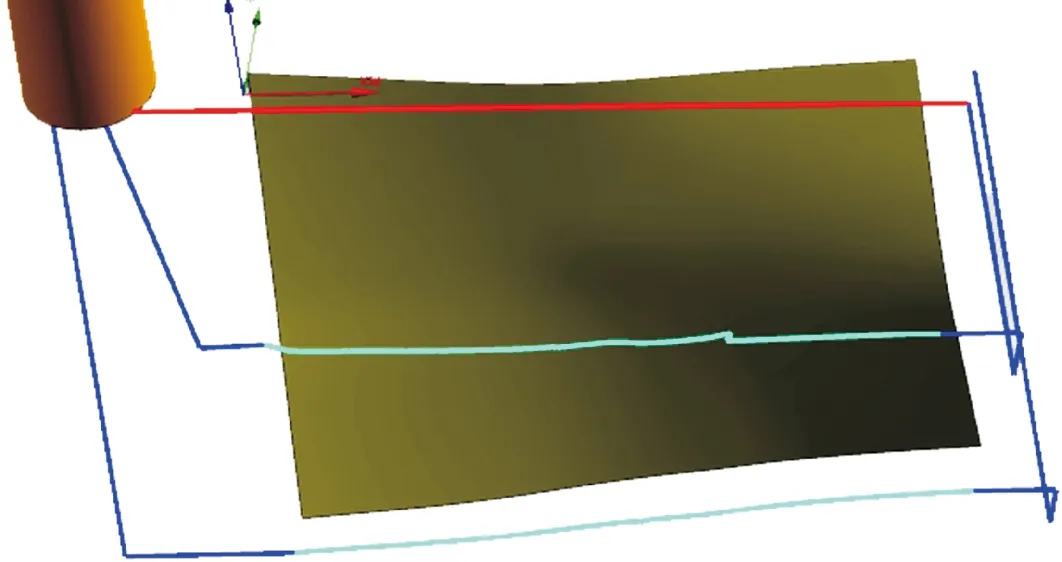
图10 样条曲面侧铣示意

将所有的刀轴矢量绘制于球面坐标系内，如图11所示。可以看出：优化前刀轴矢量基本分布于北极附近，其平均纬度较大，若直接进行后处理，则机床轴转角变化将会过于剧烈，造成加工误差严重偏离理论值。

图11 优化前后刀轴矢量的球面分布

根据提出的优化方法，将设计坐标系相对加工坐标系进行旋转，降低刀轴矢量的平均纬度。优化加工路径后的刀轴矢量在球面中的分布如图11中红色点云。通过旋转变换，刀轴矢量在球面上的平均纬度基本位于零度纬线，因此预测机床轴的转角变化会比较平缓。

将优化前后的侧铣加工路径用后置处理程序进行处理。机床转轴转角的变化情况如图12所示。绘制的转角的时间范围从主轴旋转后切削材料开始，至离开加工位置退刀结束(单次进给图线中，中断的点位表示第二行加工路径开始)。可知：机床轴和轴的转动幅度在优化后大幅降低，优化前机床轴变化范围大部分在±50°之间，并存在一个单次-150°以上的转角突变；优化后，轴转动幅度约在±5°之间，最大转角仅15°，机床转轴转动光顺性明显提升。

图12 优化前后机床转轴转角对比

在实际的加工中，加工路径优化前后得到的加工结果如图13所示。

图13 优化前后曲面的侧铣样件

从实验样件的加工效果看，未优化加工路径的样件，由于机床转轴转动幅度较大，引起了刀轴在插补中剧烈的非线性摆动，加工质量较差，因此实际加工效果与理论效果差异明显。在图13(a)中可以明显看到啃切和振纹等加工缺陷。优化加工路径后，机床转轴转角的波动程度大幅度降低，减少了刀轴的非线性摆动，因此没有啃切和振纹，曲面侧铣的实际效果基本与仿真结果一致。2个样件使用的加工路径相对于设计模型的刀位轨迹是相同的，区别在于设计坐标系相对加工坐标系的姿态不同。