基于相似度的NPLC-DSSS信号扩频码盲估计

强幸子，金 翔，张天骐

（1.安徽大学互联网学院，安徽合肥 230031；2.重庆机场集团有限公司重庆机场扩建指挥部，重庆 401120；3.重庆邮电大学通信与信息工程学院，重庆 400065）

1 引言

直接序列扩频（Direct Sequence Spread Spectrum，DSSS）是利用扩频码直接对信息码进行调制，使得传输信号频谱被展宽，并且具有低的功率谱密度，从而增强了传输信号的抗多径效应和抗干扰能力等.因此，在军事通信和民用通信等领域得到了非常广泛的应用.在通信侦察、军事对抗等特殊领域，需要利用获取的DSSS信号对其扩频码进行估计，进而完成对DSSS 信号的解扩.DSSS 信号中扩频码的盲估计研究得到了国内外学者们的广泛关注.G Burel 等人最早提出利用特征值分解的方法估计DSSS 信号的扩频码［1］.杨小牛等人利用盲源分离技术实现了直接序列码分多址（Direct Sequence-Code Division Multiple Access，DS-CDMA）多用户信号的扩频码估计［2］，该方法利用不同用户之间的独立性，有效地降低了信号解扩的误码率.

目前，针对短码直扩信号（Short Code DSSS，SCDSSS）的扩频码盲估计方法已经较为成熟.周期长码DSSS（Period Long Code DSSS，PLC-DSSS）信号可以看作是多用户的SC-DSSS信号进行处理，对该信息号的扩频序码估计研究也较为深入.但是，针对非周期LC-DSSS（Non-Period Long Code DSSS，NPLC-DSSS）信号的扩频序列盲估计问题的研究较少［3］.文献［4］提出一种基于SC-DSSS 信号的分段（Fractionation Method，FM）法，该方法将信号划分为多个时间窗远小于信息码周期的相互重叠时窗，近似认为各个时窗只包括一个信息码元，利用特征分析法实现扩频码的分段估计，并根据分段估计的重叠部分通过拼凑方式得到完整的扩频码波形估计.该方法虽然能够解决非周期LC-DSSS 信号扩频码盲估计问题，但它是建立在信息码已经同步的基础之上.

本文通过进一步研究非周期LC-DSSS 信号的结构特性，根据非周期序列中的周期规律，提出了一种新的针对非周期LC-DSSS 信号扩频序列盲估计的方法.该方法通过构造信息码库，利用平均相似度对信息码进行同步，再利用特征值分解对扩频码序列进行估计.

2 信号数学模型

在已知信号扩频码速率Rc的情况下，以Rc对NPLC-DSSS 基带信号进行采样，采样离散化后的表达式为

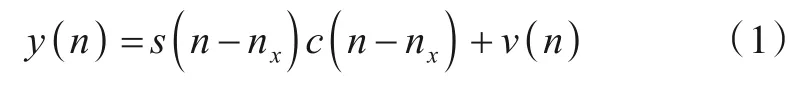
其中，s表示离散化的有用信号；c表示扩频码；v表示高斯白噪声；n=0，1，…，N-1；nx∈{0，1，…，G}为起始点信息码同步时延.

3 信号盲同步及伪码盲估计

对于NPLC-DSSS 信号，扩频码与信息码的长度不为整数倍关系，且扩频码周期大于信息码周期［5］.故，在调制过程中，信息序列符号的极性变化会严重扰乱扩频序列的周期性和自相关特性，导致序列估计的难度增大.本节通过深入研究NPLC-DSSS 信号的结构特性，根据非周期序列中的周期规律，提出了一种新的针对NPLC-DSSS 信号扩频序列盲估计的方法.首先利用平均相似度对信息码库进行匹配，估计出信息码的同步位置，随后，利用相似度的特性对NPLC-DSSS 信号的周期性进行恢复，最后利用特征值分解对扩频码进行盲估计.其算法结构框图如图1所示.

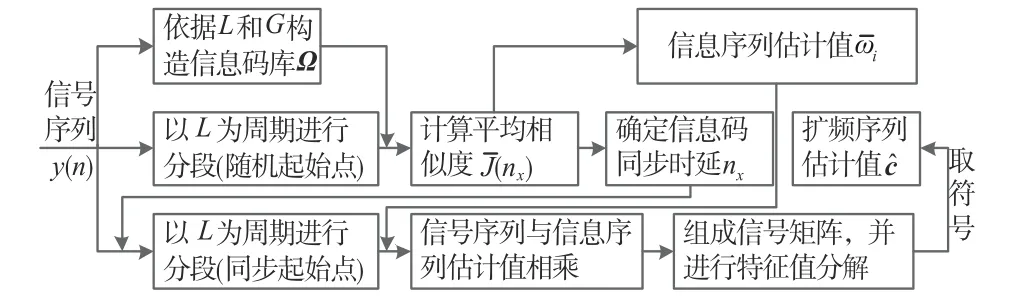
图1 基于相似度的NPLC-DSSS信号扩频序列估计框图

3.1 信号结构分析

在y(n)中，令

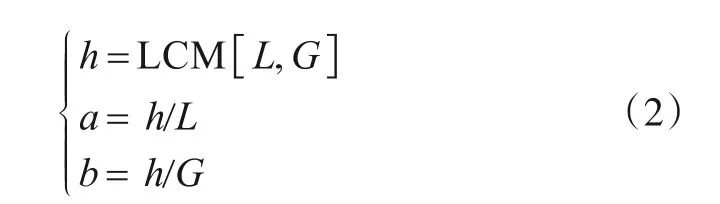
其中，LCM[L，G]表示L，G之间的最小公倍数.其结构如图2所示.nx表示信息码的起始位置与扩频序列的同步时延；na表示第a个扩频周期中信息码的同步时延；si表示第i个信息符号.

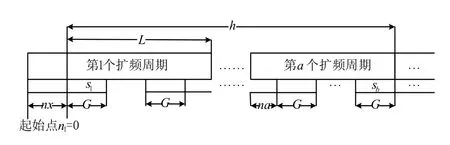
图2 y(n)的结构示意图

根据L和G之间的关系，当nx=0 时，第i个扩频周期中信息码的同步时延为

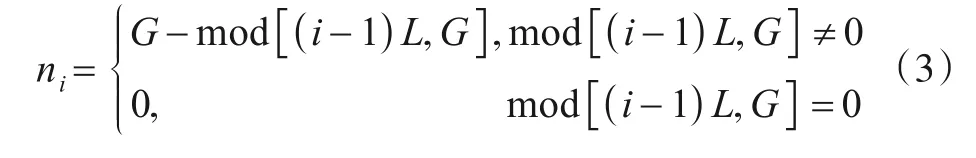
同时，在图2中长度为h的数据内，有：

性质1任意两个扩频码的周期内信息码与扩频码同步时延均不相同，即

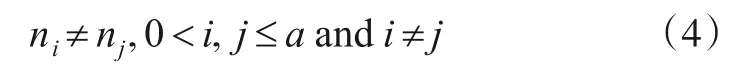
同时，对接收信号以h进行分段，序列是一个以a为周期的周期序列.（证明略）

性质2假设第i个扩频周期对pi个信息符号进行了调制，则

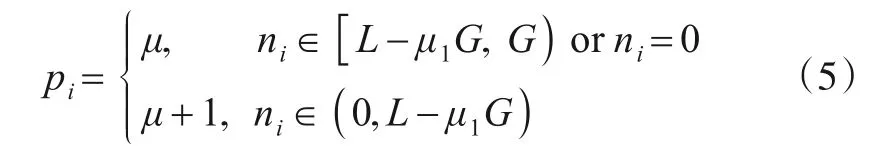
3.2 信息码盲同步过程

假设起始点的信息码同步时延为nx，对数据序列y(n)以扩频码长度L进行分段，并将第i个扩频周期内的信号用向量yi表示

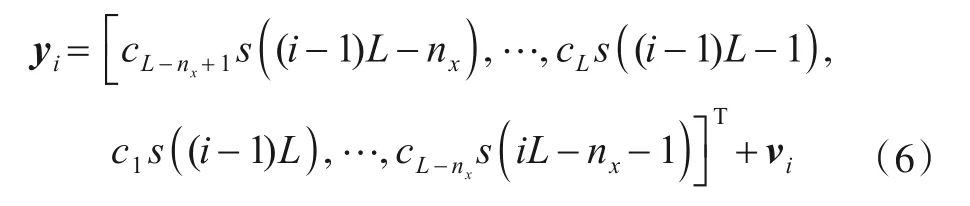
其中，vi表示噪声序列.根据性质1，当同步时延为零时，我们可以直接得到每个扩频码周期内的信息序列与扩频码之间的时延序列，而当同步时延为τx时，在每一个L长度的分段数据中，其同步时延可另写为′，并且有

因为Ωi中调制的第一个信息符号假定为“+1”（Ωi中的前ni行均为“+1”），若nx=0，Ωi中必然有一列与第i个扩频码周期内调制的信息序列相同或符号完全相反，并且只有一种情况.

在连续a个扩频周期内的任意两个扩频周期间的相似度定义为

利用上述特点，我们可以通过滑动改变接收数据的起始位置，利用平均相似度最大的特点估计同步时延nx.考虑到低信噪比条件下的扩频码估计，我们对每个h数据段内的平均相似度进行累加再平均.即

其中，CM表示相似度平均次数.随着M的增大，时延nx的估计越准确.当滑动接收信号起始点位置时，在nx=0时，平均相似度函数取得最大值.

3.3 基于相似度的扩频码估计

定义

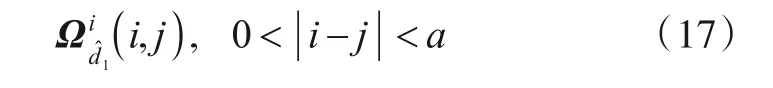
表示当nx=0 时，第i个扩频周期与第j个扩频周期做相似度分析取最大值时所匹配的Ωi中的对应列向量.那么,即为第i个扩频周期中扩频码所调制的信息码或其反码的估计值

由于Ωi中只列出了每个扩频周期中一半的可能性，因此对于每个扩频周期来说，在Ωi中只能找到其信息序列的原码或反码的一种.即当固定i时，式（18）中j在其取值范围内取不同值时，得到的是相 同的.为了提高信息序列估计的抗噪性能，本文采用平均累加的方法对进一步校正

根据3.2 节估计得到的nx，在图2 中，以nx+1 为信号起点的接收信号可写为

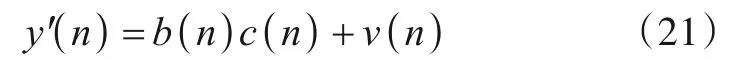
对其以L为周期进行分段，第i个扩频周期内的序列用向量表示

其中M表示接收信号包含的扩频周期数.

对进行特征分解，其特征分解矩阵表达式为

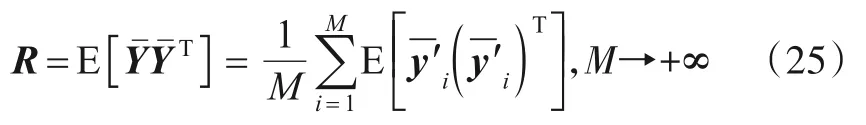
其中E(·)表示取期望，因为信号和噪声是相互独立的，噪声的均值为零，方差为.将式（23）代入式（25），对上式进行化简有

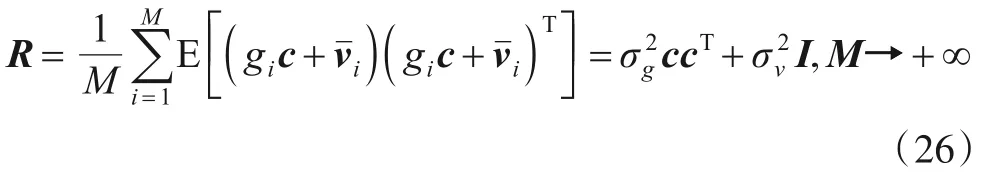
其中I表示L×L的单位矩阵，表示信号方差.

矩阵R可写为

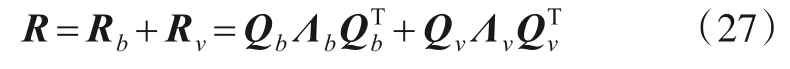
其中矩阵Qb和Qv中的列向量分别由矩阵R的特征值所对应的特征向量构成，此时特征值对角矩阵为Λb=diag(λ1)和噪声方差对角矩阵为Λv=diag(0，λ2，…，λi)，则R的特征值排列分别为

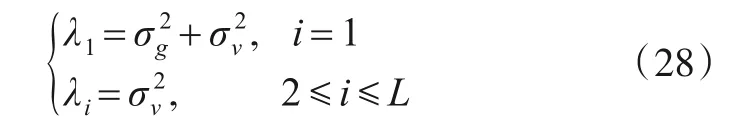
由上式可知，只有一个较大的特征值λ1；对其对应的特征向量取符号即为扩频码c的估计值

3.4 计算复杂度分析

本文算法主要包括信息码库的构建与匹配，平均相似度的计算以及信号矩阵的特征值分解.其中，信息码库的构建与选择的计算量约为O(22μ).在选择信息码库的基础上，平均相似度算法的复杂度约为o(22μML2)［6］；采用三角分解对矩阵进行特征值分解的算法复杂度约为o(ML2)［7］；因此，本文算法的整体复杂度约为o(22μML2+ML2).

4 仿真实验及性能分析

在本文仿真实验中选用BPSK 调制NPLC-DSSS 信号，接收信号长度用扩频周期数M表示.扩频码用随机生成的方式产生，其长度L=127；信息码元宽度G=30.信道噪声为加性高斯白噪声.本文采用信噪比（SNR）和比特误码率作为扩频码估计的性能指标：

4.1 信息码同步时延检测性能

信息码同步位置的正确检测概率随着信噪比变化的性能曲线如图3 所示.由图可见，随着接收信号长度M的增加，该算法检测同步位置的抗噪声性能不断提高.

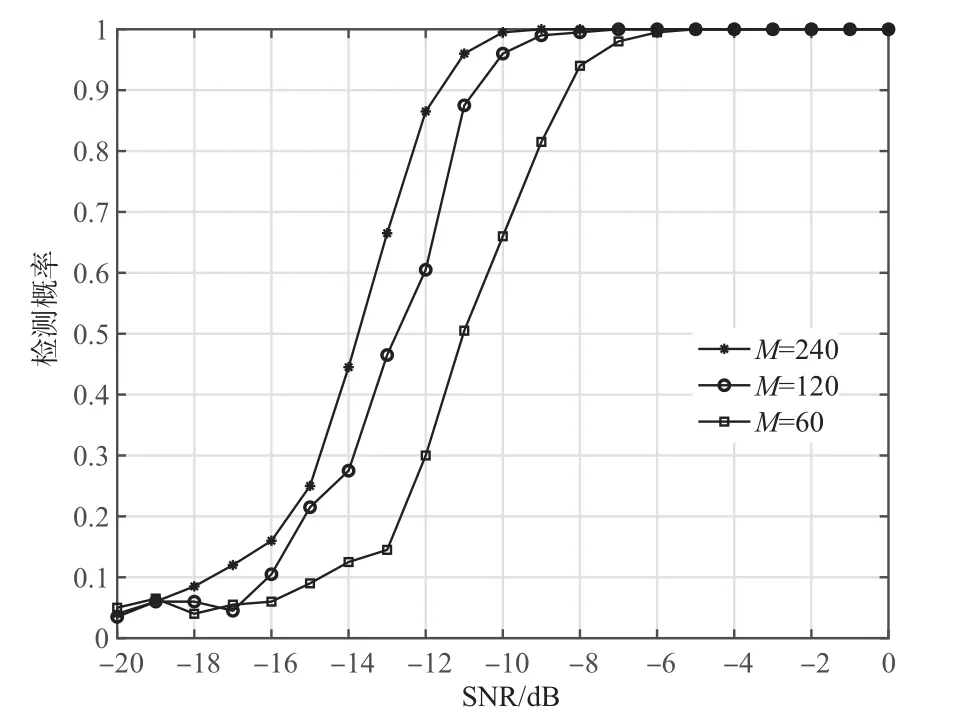
图3 信号同步位置检测概率

4.2 扩频码估计性能

图4 给出了接收信号长度M=1000，SNR=-11 dB时，采用本文算法估计得到的伪码序列与真实伪码序列的对比.图中，伪码序列的估计值是伪码序列真实值的反序列，该现象叫相位模糊现象，其符合前面的理论分析.

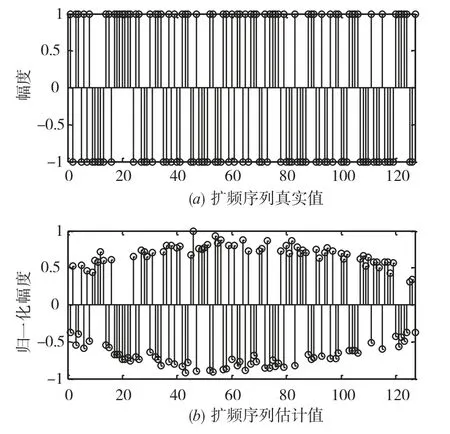
图4 扩频序列估计样本图

接收信号在不同信噪比条件下，本文算法通过200次蒙特卡洛仿真实验估计伪码序列的比特误码率曲线如图5 所示.由图可见，当固定M时，随着信噪比的增大，伪码序列估计值越准确；同时，在相同信噪比条件下，随着M的增加，伪码序列的估计值越准确.

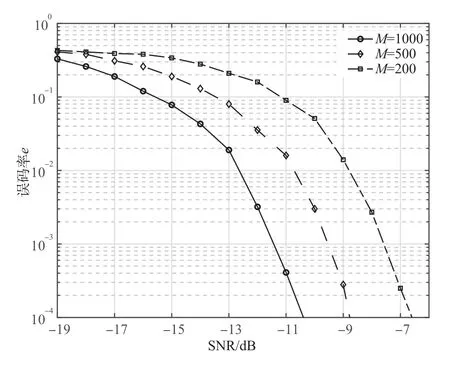
图5 所提算法伪码序列估计性能曲线

图6 给出了在相同信源条件下M=1000，L=127，G=30，本文算法与分段估计法在不同信噪比条件下的性能对比曲线.由图可知，两种算法随着信噪比的增加，估计伪码序列的性能都不断提高；在相同信噪比条件下，本文算法估计伪码序列的性能优于分段估计法.当误码率为10-3时，所提算法与FM 算法的信噪比分别为-11.385 dB和-10.307 dB.因此，本文算法较FM 算法抗噪性能提高了1 dB.

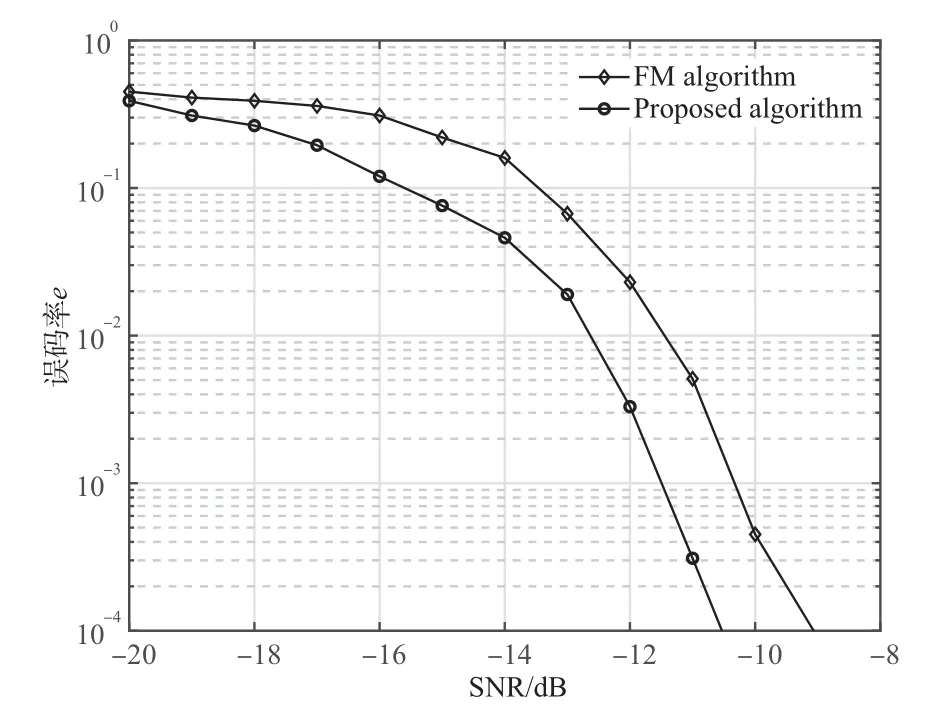
图6 所提算法与FM算法估计性能比较

5 结论

本文对NPLC-DSSS 信号的结构特性进行了分析，通过构造信息码库，利用平均相似度和特征分解对信息码同步位置和伪码序列进行联合盲估计.仿真实验表明，本文算法较现有算法计算量有所增加，但在信源条件相同的情况下，使得伪码序列估计的抗噪声性能提高了1 dB，而且在极低信噪比条件下能够对信息码同步位置进行准确估计.同时，该算法每次运算只限于两个伪码周期内的信号序列，内存开销不大，易于工程实现，具有一定的理论意义和应用价值.