粒子群算法优化的液压球形关节自抗扰控制研究

任洵涛,边斌,王亮

(1.中国船舶集团有限公司第七〇四研究所，上海 200031；2.北京航空航天大学自动化科学与电气工程学院，北京 100191)

0 前言

球面运动作为一种仅次于旋转运动的重要运动类型，在工业生产中得到了广泛应用，如灵巧眼和机器人关节，目前其主要实现形式有串联机构和并联机构。串联机构存在关节累计误差大、末端定位精度低和刚度小的缺点，而并联机构往往工作空间较小，存在较多奇异位形。液压球形关节作为一种球面运动机构，不需要中间传动装置，仅通过单一关节便可以实现两个自由度的光滑球面运动，具有结构紧凑、转动惯量小和刚度大等优点。

集成式的液压球形关节系统具有多输入多输出、非线性和模型不确定性等特点，虽然传统PID控制具有结构简单和易于实现的特点，但是很难满足这种复杂非线性系统的控制需求。自抗扰控制(Active Disturbance Rejection Controller，ADRC)作为一种不要求系统精确动力学模型的控制方法，在系统动力学模型难以精确建立和非线性系统的控制中得到了广泛应用。刘春强等在永磁同步电机伺服系统的控制中采用三阶扩张状态观测器，设计了位置-电流双环非线性ADRC，取得良好的控制效果。姜伟等人为了削弱时变扰动和模型不确定性的影响，在工业机器人关节伺服控制系统设计过程中，提出了一种基于惯量估计的变增益ADRC，提高了系统的动态性能。

然而，非线性ADRC引入了非线性项，需要调节的参数较多，且整定困难，限制了其在实际工程中的应用。为了能够有效调节参数，齐晓慧等利用BP神经网络对扩张状态观测器(ESO)的参数进行在线调整，提升了系统的抗干扰能力，但是受BP神经网络设计质量的影响，有一定的局限性。李扬等人利用动态响应过程中时序数据关联关系挖掘的方法对自抗扰控制中误差反馈律参数进行整定，并未对ESO参数进行自整定。王丽君等在双输入双输出热连轧板宽板厚控制系统设计过程中，利用具有全局快速搜索能力的变尺度混沌优化方法对ADRC参数进行优化，一定程度上提升了ADRC的抗扰能力。

综上，利用智能优化算法对ADRC参数进行整定是一个研究的热点。本文作者在液压球形关节控制系统设计过程中，采用一种以时间乘以绝对误差积分为优化准则(ITAE)的改进型粒子群优化(Particle Swarm Optimization，PSO)算法，对ADRC的参数进行在线自整定。介绍液压球形关节的结构，建立其动力学模型；介绍非线性自抗扰控制器的原理，分析改进型PSO算法的优化过程，并将改进型PSO融合到ADRC参数调整过程中；通过MATLAB/Simulink进行仿真研究，验证算法的有效性。

1 液压球形关节结构及工作原理

图1所示为液压球形关节结构，它具有绕轴旋转角的偏转和绕轴旋转角的横滚两个自由度，可以实现以点为中心的球面运动。该机构主要由下定子、舵叶、滑轨、上定子、上转子和下转子等组成，所有球形构件具有相同的中心。

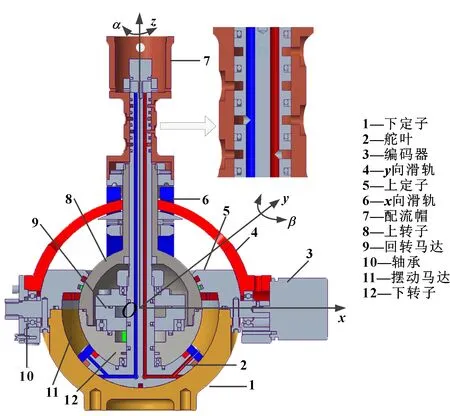
图1 液压球形关节结构示意

作为执行机构的回转马达和摆动马达集成在舵叶和转子上，其中，回转马达是一个超全周马达，可以实现超全周运动，如图 2所示。向滑轨和向滑轨通过轴承安装在上定子上，其与编码器组成了转角测量系统，利用滑轨实现运动在和方向上的定向，通过编码器测量转动角度。同时，两个马达的进油口和回油口均布置在舵叶轴上，与舵叶轴上布置的密封圈和配流帽形成了两套独立的配油系统。

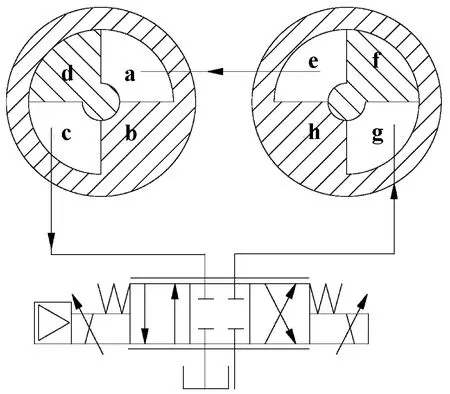
图2 回转马达原理

2 液压球形关节动力学模型

将=[]作为广义坐标系建立液压球形关节的动力学模型，可表示为

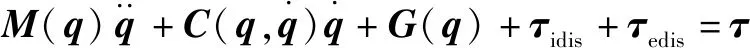
(1)

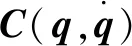
根据液压球形关节工作原理可知，活动部件分别为舵叶、转子和回转马达，其转动角速度分别为

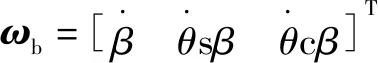
(2)

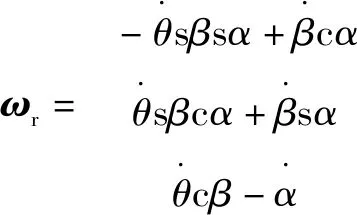
(3)

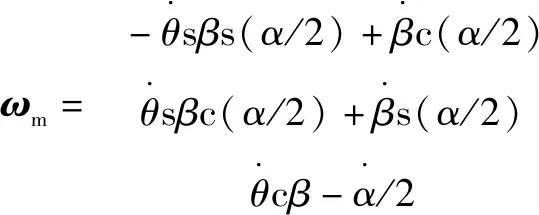
(4)

式中：为转子绕定子坐标系轴的转动角度。c和s分别代表cos和sin。

利用拉格朗日法可以求得液压球形关节的动力学模型：

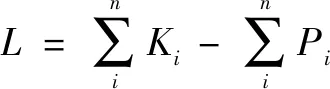
(5)

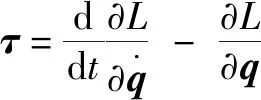
(6)

=diag(,,,)

(7)

式中：为拉格朗日函数;和分别为运动部件的动能和势能，=b,r,m;代表运动部件的转动惯量。

=+secc(tan+c)[sec-(tan+c)]

==tansc(tan+c)[sec-

05(tan+c)]

=+tans)tan+c)

=0

=-(++)s

3 自抗扰控制的基本原理

自抗扰控制是韩京清研究员提出的一种结合现代控制理论成果和PID思想精髓的非线性控制器，将系统未建模动态和外界扰动等未知信息均视为扰动，通过输入输出信息进行估计并补偿，以实现动态估计和反馈补偿。它主要由跟踪微分器(TD)、扩张状态观测器和非线性状态误差反馈控制律(NLSEF)组成，如图 3所示。跟踪微分器可以从含有噪声的信号中提取出实际信号，降低甚至消除噪声对信号的影响，同时给出近似的微分信号。

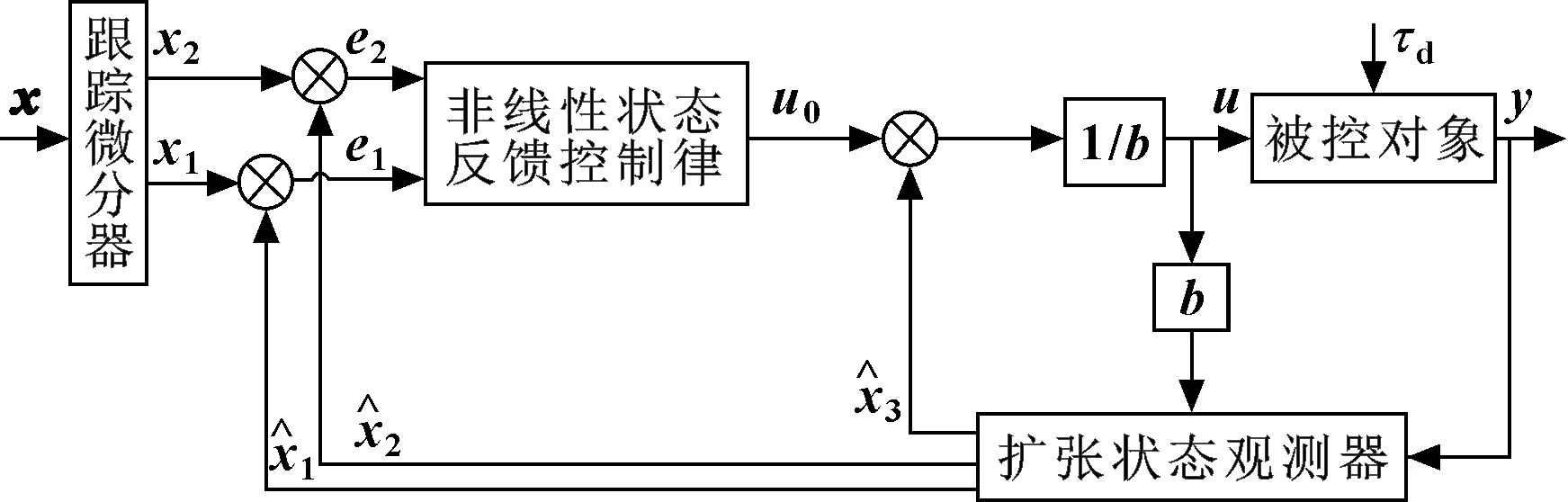
图3 ADRC结构

3.1 扩张状态观测器设计

引入扩张状态后，以运动方向为例进行计算，式(1)所示的液压球形关节动力学模型的状态空间表达可扩张为

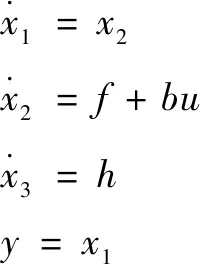
(8)

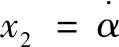
针对上式设计非线性扩张状态观测器为

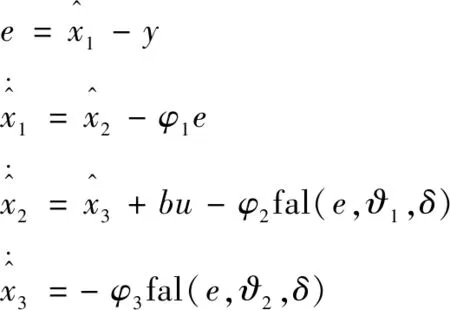
(9)

式中：

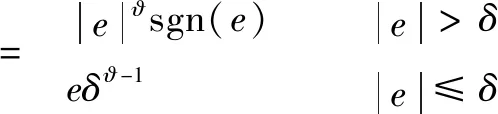
(10)

引入误差阈值可以把||sgn()改造成在原点附近具有线性段的连续的幂次函数，避免小误差时由高增益引起的高频颤振现象。通常ϑ=05、ϑ=025，一般以0.01为基点进行调节。、和为观测器增益系数，和越大跟踪信号的速度越快，同时可以抑制过大产生的系统振荡；越大估计的扰动相对于实际滞后越小。

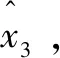
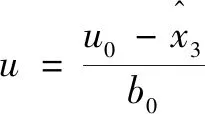
(11)

则：

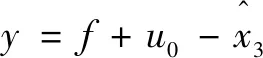
(12)

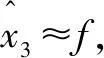
小学数学是一门基础性的课程，对学生今后很多方面知识学习都有着中重要的帮助。而在小学数学教学中，开展综合实践活动课，提高了小学生的综合实践能力，但教学过程中依旧面临着一些教学问题，这就需要使用有效的措施进行改进，解决存在的各种问题，提高整体的教学质量。

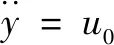
(13)

上述动态线性化过程将系统转化为积分串联型系统，此时可以进行基于误差的线性或非线性反馈控制律的设计。

3.2 线性状态误差反馈控制律设计

为简化设计，采用PD控制作为误差反馈控制律：

=+

(14)

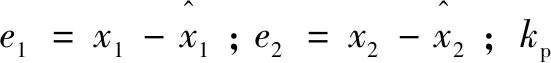
则闭环传递函数为

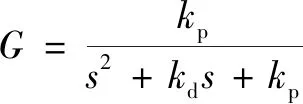
(15)

所以，增益可以设计为

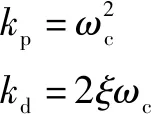
(16)

因此，扩张状态观测器需要整定的参数为、、和。如果系统未建模动态和参数偏差较大，会严重影响其他参数的整定效果。目前，没有系统性的参数整定方法来指导这些参数的调节，仍然以手动调节为主，工作量较大且效果不佳。本文作者采用一种改进型PSO整定ADRC参数，实现参数的在线自动优化。

4 基于改进型PSO的参数自整定ARDC

4.1 粒子群优化算法

粒子群优化算法是一种模拟自然界生物觅食规律，借助过程中个体和种群信息流，从一组随机初始解出发开始寻优的方法，它具有算法简单、计算效率高的优点，广泛应用于参数在线寻优的问题。其数学表达如下：

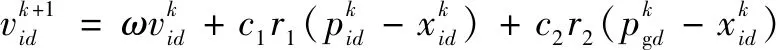
(17)

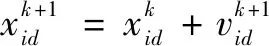
(18)

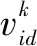
4.2 算法的改进

惯性权重用于调节对解空间的搜索范围，其值越大，全局搜索能力越强，易得到全局最优解；反之，容易陷入局部最优，所以取值对PSO算法的参数优化效果至关重要。常用的线性递减策略容易出现过早收敛的问题，本文作者采用改进的非线性动态方式更新，此方法与线性递减策略相比，全局和局部搜索能力均较强，收敛速度和稳定性更好。公式为

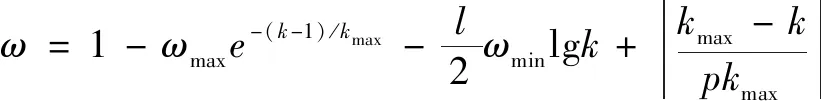
(19)

式中：和分别为最大和最小惯性权重;为最大迭代次数;为当前迭代次数;和为控制因子。

4.3 基于改进型PSO算法的ARDC参数优化

利用改进型PSO算法对ADRC参数进行在线优化整定，采用时间乘以绝对误差积分(ITAE)作为优化性能评价指标：

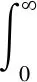
(20)

将、、和4个参数作为PSO的粒子，则基于PSO参数优化的流程如下：

(1)初始化粒子群，随机产生粒子的位置和速度，设定粒子群算法的参数；

(2)将初始值代入到控制器并计算评价性能指标ITAE，判断是否满足判定条件，满足则结束，不满足则继续进行步骤(3)；

(3)根据当前适应度函数值和个体与全局最佳位置，确定个体最佳位置和全局最佳位置g；

(4)根据位置和速度迭代计算公式更新粒子的位置和速度，并返回步骤(2)。

5 仿真研究

为验证基于改进型PSO算法的ADRC参数优化算法的有效性，针对液压球形关节的运动控制问题，利用MATLAB中的Simulink工具箱对所采用的控制器进行仿真研究。控制算法流程如图 4所示。

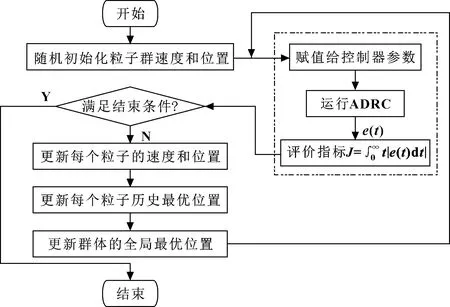
图4 基于改进型PSO算法的ADRC参数优化算法流程

在和方向分别采用幅值为1 、0.785 rad的阶跃信号作为输入信号。控制器中PSO和ADRC的参数见表1。

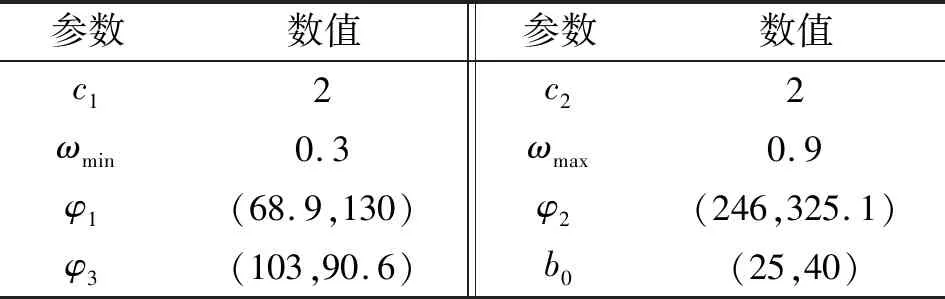
表1 PSO和ADRC参数

基于改进型PSO算法优化前后液压球形关节系统在和方向的阶跃响应曲线分别如图5和图6所示。自优化过程中、、和的参数自整定过程如图7和图8所示。由图5、图6可以看出：与传统的ADRC比较，经过改进的PSO优化的ADRC在和运动方向上超调量分别减小约0.3、0.13 rad，调节时间分别缩短了约0.98 s和0.59 s。因此，使用改进PSO算法优化ADRC的参数对控制器进行寻优是一种可行的方法。

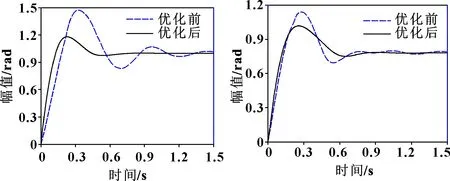
图5 α阶跃响应曲线 图6 β阶跃响应曲线

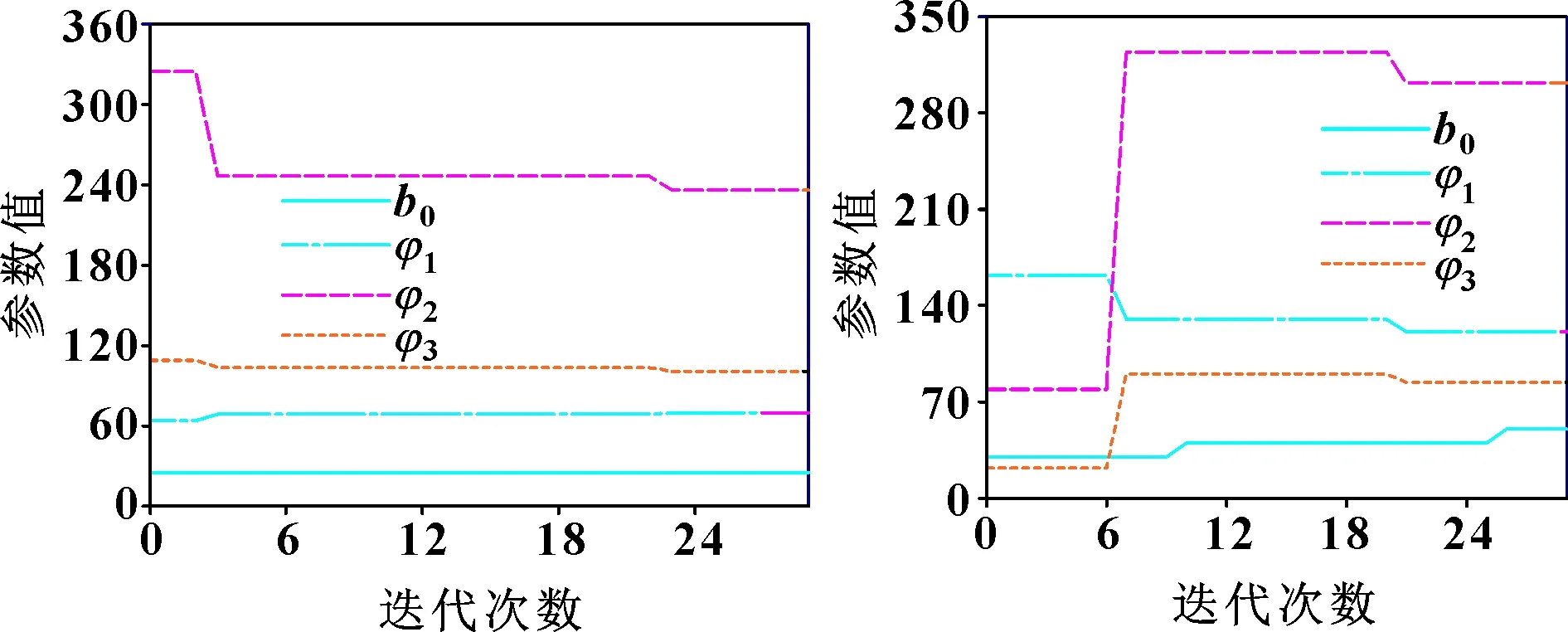
图7 α参数优化迭代 图8 β参数优化迭代

6 结论

以液压球形关节为研究对象，针对其多输入多输出、非线性和模型不确定性等特征，ADRC需整定参数多的问题，采用一种基于改进型PSO算法对ADRC参数进行在线自整定的方法，对控制性能进行寻优。通过MATLAB/Simulink建立了控制系统模型，仿真结果验证了算法的有效性。相比手动参数调节的ADRC，基于改进型PSO参数自整定的ADRC具有更小的超调量和更短的调节时间，性能更优越。因此，利用改进型PSO对ADRC参数寻优是一种提升控制器性能的有效方法。