机器学习驱动的大类资产因子配置研究
2022-09-17周亮蒋练
周 亮 蒋 练
(1.湖南财政经济学院财政金融学院,湖南 长沙 410205;2.湖南师范大学商学院,湖南 长沙 410081)
一、引言
自Fama 和French (1993)提出三因子模型以来,因子投资便成为投资理论研究及实践应用的焦点,之后大量新的因子被提出并得到广泛应用。如Carhart(1997)基于美国共同基金数据提出了动量因子(李富军等,2019),Amihud(2002)基于换手率数据提出了非流动性因子,Ang 等(2006)在发现低风险异象的基础上提出了异质波动率因子,Fama和French(2015)在三因子的基础上增加了投资因子和盈利因子构造了五因子模型等(赵胜民等,2016)。除此以外,行为金融学的大量研究成果也被应用到因子构建上,最具代表性的是投资者情绪因子(Sun 等,2016;余传明等,2018)。随着数据的丰富和计算机性能的提高,越来越多的因子被挖掘出来,形成了Cochrane(2011)所说的“因子动物园”。Harvey 等(2016)发现在顶级金融学术期刊和SSRN 高评价工作论文上的定价因子多达316 个,其中59 个新因子是在2010—2012年短短三年间提出的。但是这么多因子并不都是有效的,Green 等(2017)和Hou等(2020)的研究发现,大部分因子在后续的样本外检验中难以持续地提供超额收益。因此,在处理如此众多的因子时,必须使用不同的研究工具(Cochrane,2011)。在此背景下,在处理非线性及共线性关系方面表现颇佳的机器学习模型得到了金融理论界和实务界的广泛关注。
机器学习具有以下优势,使得其在金融领域表现出显著优于传统计量建模技术的能力:第一,大部分机器学习技术设计的初衷就是用来进行预测,如多层神经网络能够逼近任意非线性函数,基于树模型的boosting 算法能够根据预测误差不断更新样本权重,因此,相比于传统的计量经济模型,机器学习模型的预测能力显著较高(Gu 等,2020)。第二,传统计量经济模型只能处理有限变量,当变量数量较多且存在共线性等问题时,模型拟合能力及外推能力将会大幅降低,但是机器学习模型利用变量筛选及降维等技术,可以有效解决共线性问题,从而可以向模型中添加大量变量,保证模型输入信息的全面性、系统性(Bluwstein 等,2020)。第三,决策树、支持向量机、神经网络和集成学习等机器学习算法均能对非线性函数进行逼近,能够通过参数寻优拟合变量间的非线性关系,而传统的计量建模技术只能拟合线性关系,或者通过在模型中添加变量的高阶项或交互项对非线性关系进行部分拟合。具体到因子投资领域,国内外大量学者利用各种公司特征或技术指标作为自变量,构造了机器学习的选股模型,无一例外,均发现模型具有较好的选股或择时能力(李斌等,2019)。
综上,学者们对因子投资以及机器学习选股进行了大量研究,但是存在着两方面的改进空间:一是现有研究大部分聚焦于直接进行资产配置,但是正如Bass 等(2017)和Bender 等(2019)所指出的,基于因子的配置方法将资产配置的决策过程从资产层面转向更为微观的因子层面,投资者能够通过其对因子收益分布以及相关性的预测更好地进行资产配置(周亮和李宁,2021)。二是现有研究较少涉及机器学习最广受诟病的“黑箱”属性,对于金融投资而言,如果不清楚模型的内部构造及运行机制,必然导致投资者在模型失效时容易丧失信心,从而不敢轻易使用。
基于此,本文选取2004年1月—2021年12月我国股票市场、债券市场及商品期货市场的8 个大类资产因子作为研究对象,利用随机森林(Random Forrest,RF)模型构造了因子配置模型,并利用特征重要性及部分依赖图(Partial Dependence Plot,以下简称PDP)等方法对模型进行解构,以打开机器学习的“黑箱”。相对于已有研究,本文的可能贡献在于:一方面,不同于常见的多因子模型或二次规划,本文利用机器学习模型,从非线性角度构造投资组合,拓展了投资组合理论的研究边界,同时通过解构变量的相对重要性、非线性影响以及交互作用,部分打开了机器学习的“黑箱”;另一方面,将资产配置的研究视角拓展到因子层面,有助于投资者深入理解投资收益和风险的关键驱动因素,明确风险和收益的来源。
二、研究设计
(一)随机森林模型
机器学习模型众多,不存在所谓的最强模型,不同的数据、不同的问题适用不同的模型。其中,随机森林方法结构简单,参数少,过拟合概率低,同时还具有非常强的样本外预测能力。实证显示,随机森林模型得到的多空组合在收益性和稳健性上都优于传统的线性模型,更重要的是它可以帮助我们省去“因子筛选”“因子加权”和“线性转换”的中间过程,提升预测效率。
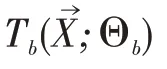
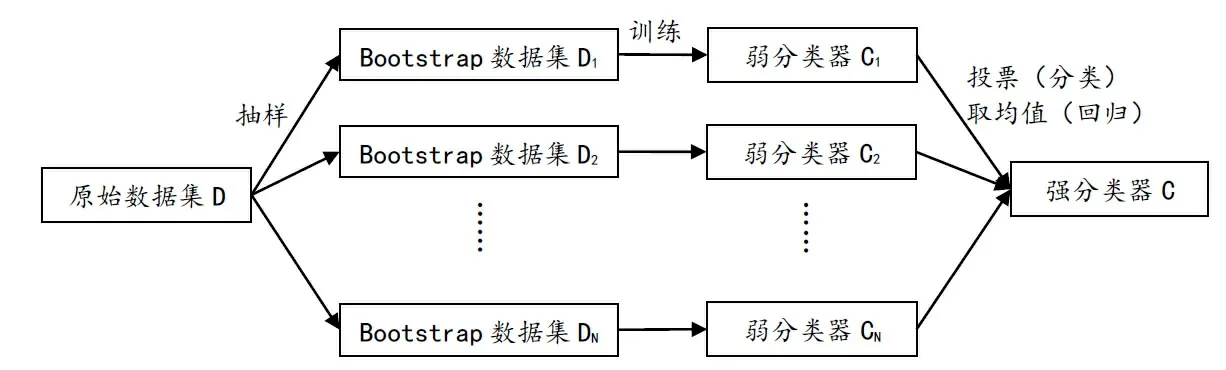
图1:随机森林模型原理图

CART 对数据很敏感,随机森林算法使得它生成的决策树预测结果的相关性很低,但偏差变化不大,因此,把多个低相关性的预测结果组合在一起,方差会明显降低。随机森林是通过降低预测结果的波动性来提升样本外预测的准确度,其性能通常要比单个决策树和许多其他机器学习算法好得多(Fernández-Delgado 等,2014;周亮,2021)。随机森林有两个重要参数,分别是决策树的数量以及每个决策树所使用的特征数量。为了避免模型过拟合,本文均使用模型的默认参数,决策树数量为500 棵,每个决策树所使用的特征数量为6 个(即18/3,本文共选择了18个特征)。
(二)模型检验指标
为了对模型预测绩效进行评估,本文除选择常见的RMSE、MAE 及Theil-U 进行评估外,还选择了方向预测准确度DAR 及可决系数,计算公式分别如式(2)—(6)所示。
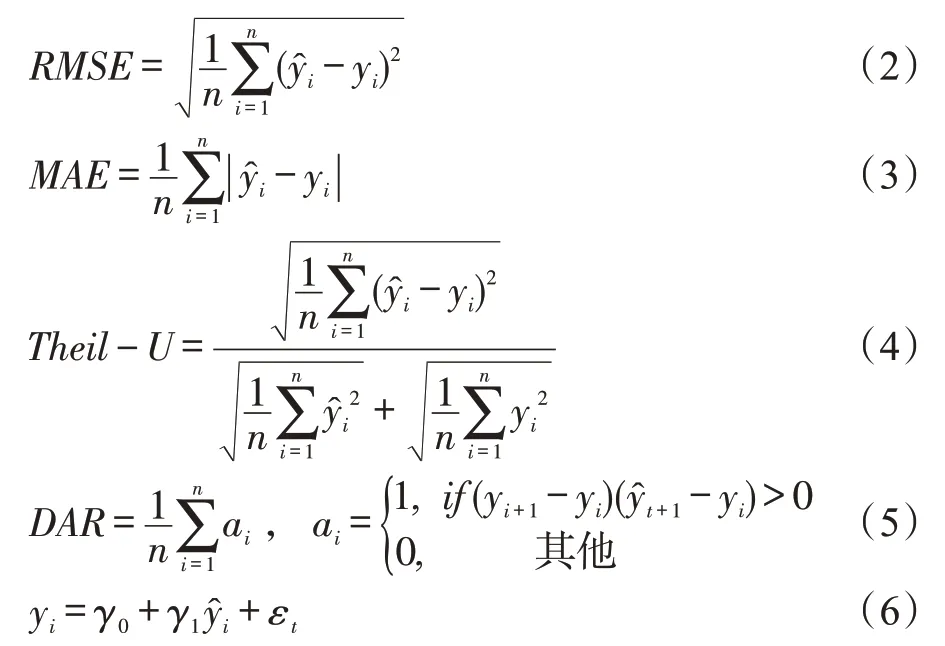
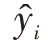
(三) PDP方法
本文除了采用特征重要性分析评估随机森林模型中各特征的相对重要程度外,还利用PDP方法探讨了特征的非线性影响以及特征间的交互作用。PDP的核心思想是考察某项特征的不同取值对模型输出值的影响,如图2所示。将某项特征X全部设为常数,其余特征保持不变,可得到一组新的模型输入值X,再利用原模型进行预测,比较预测值与初始预测值的差异,从而可以观察到每个变量的相对重要性。
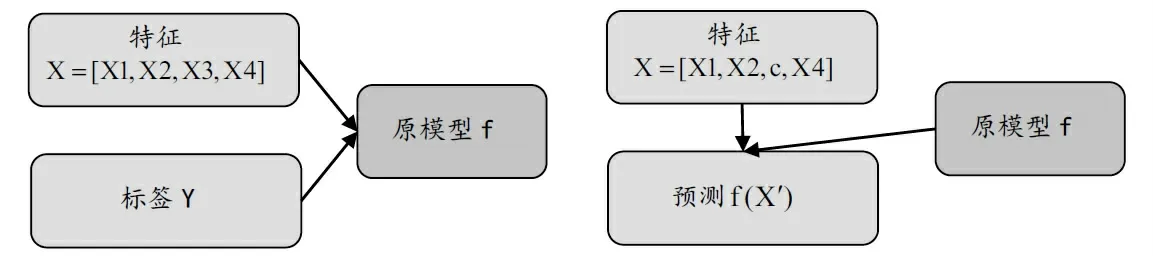
图2:PDP方法检测特征重要性
(四) 指标选取及样本说明
为了检验随机森林模型在大类因子配置上的预测能力,本文选择了6 个常见的股票类因子(包括市场因子MKT、规模因子SMB、估值因子HML、盈利因子RMW、投资因子CMA、动量因子UMD)、1 个债券因子(BOND)、1 个商品期货因子(METAL)的周数据作为分析对象,样本周期为2004年1月至2021年12月。股票类因子中市场因子为沪深300指数的收益率,规模因子、估值因子、盈利因子、投资因子的构造方法参照Fama-French 五因子模型,动量因子参照Carhart 四因子模型;债券因子用中证全债指数收益率衡量;商品因子选择了收益相对较高的南华金属期货指数收益率来衡量。随机森林模型中,因变量为因子当期收益率r,在特征(自变量)选取上,我们选择了18 个常见的指标,包括动量、波动率、技术面指标以及宏观指标等,具体如表1所示,其中ˉ为收益率均值。因子数据来自BetaPlus 小组(www.factorwar.com),其他数据来自万得数据库。
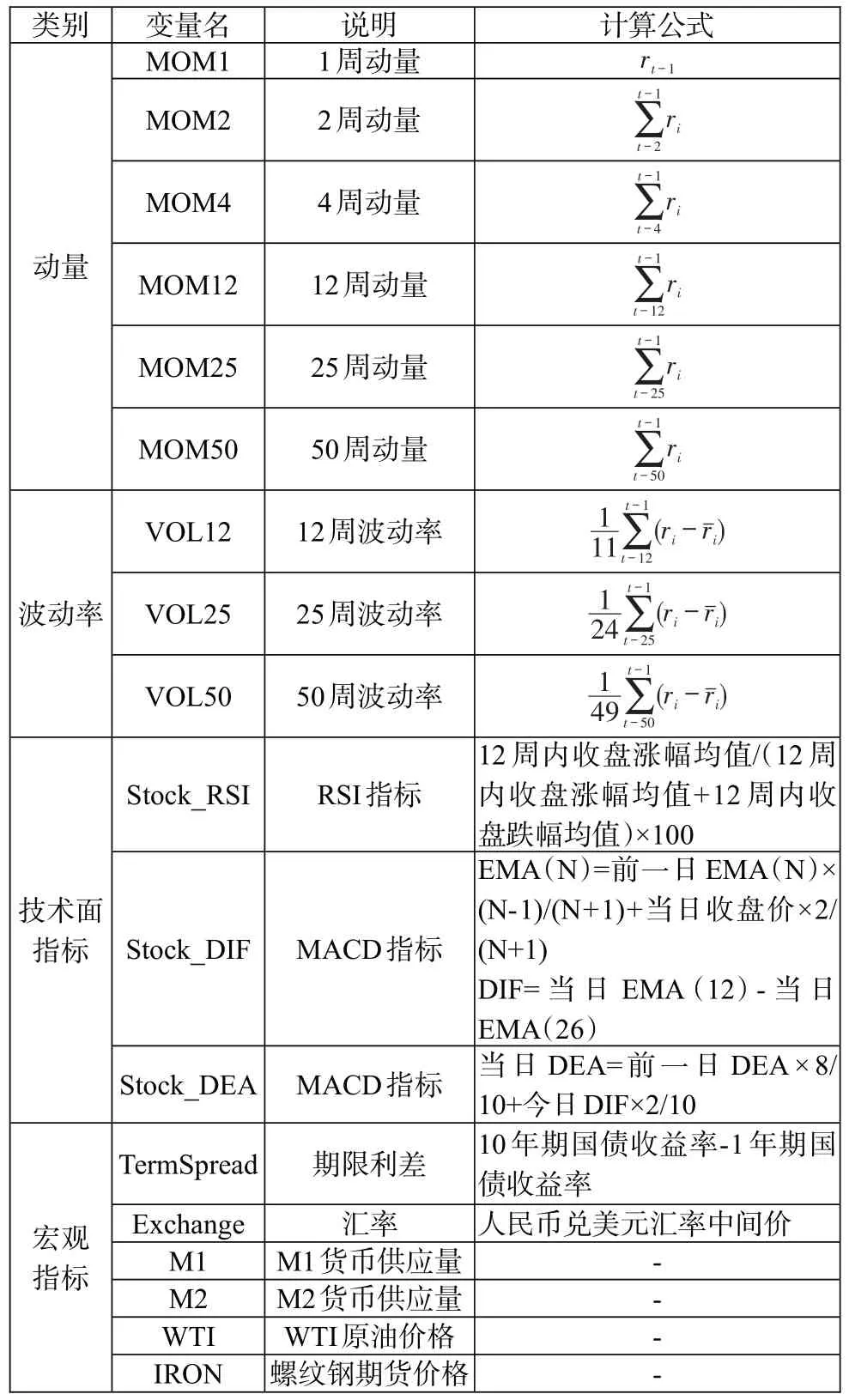
表1:指标及其说明
三、实证结果及分析
(一)因子描述性统计
表2报告了所选因子的描述性统计结果。可以看到,在所选样本期内,估值因子HML 和投资因子CMA 表现不佳,年化收益率均为负值,说明二者在我国股票市场的整体有效性不强;动量因子UMD 表现也较为一般,年化收益率仅为0.33%,这符合大部分学者的研究结论,即动量效应在我国股市并不明显;市场因子MKT 和商品期货因子METAL 表现较好,年化收益率分别达到了9.51%和9.38%,说明整体来看,我国的股市及商品期货(有色金属)市场保持了稳定的上升趋势;除此以外,规模因子SMB 及盈利因子RMW 在样本区间也具有一定的有效性;债券因子BOND 虽然年化收益率只有4.44%,但是其风险远低于股票类和商品期货类因子,年化波动率仅为2.13%,最大回撤也仅为4.06%,因此,其风险调整后收益(用夏普比率、索提诺比率及卡尔玛比率衡量)远高于其他因子。
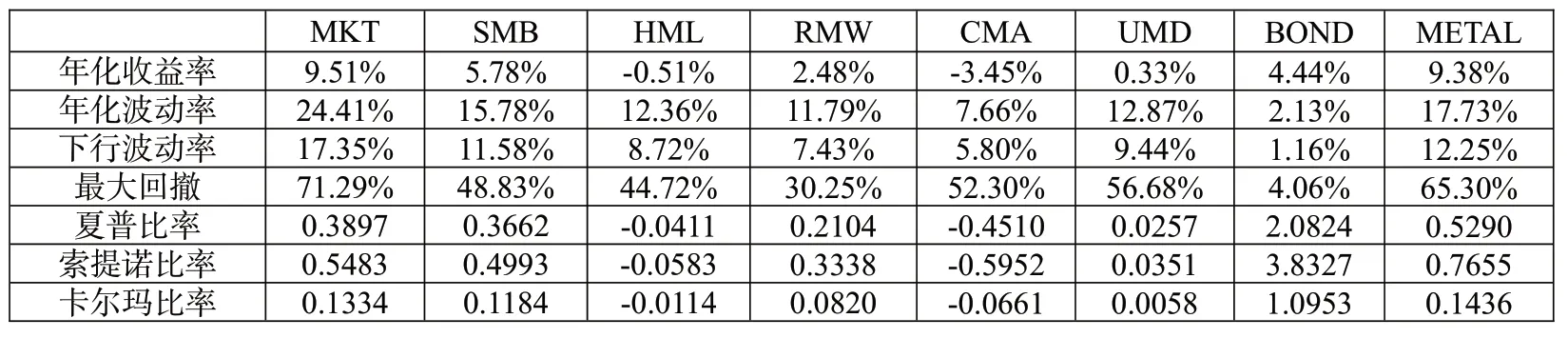
表2:因子描述性统计
图3展示了部分因子的净值曲线,可以看到,相对于其他因子,盈利因子RMW 及债券因子BOND 表现较为稳定,但是由于收益不高,最终净值远低于其他三个因子;规模因子SMB 在2016年以前有效性非常强,但是从2017年开始出现了显著回撤;商品因子METAL 在2015年以前波动较为剧烈,净值几乎没有上涨,但是从2016年开始进入大牛市,最终净值高达5.37;市场因子MKT 虽然最终净值高达5.5,但是波动也非常剧烈。从图3总体来看,各因子之间的相关性较低,更详细的相关性分析结果见表3。从表3可以看到,大部分因子间的相关系数很低,只有规模因子SMB 和投资因子CMA 的相关系数略高于0.4;很多因子间的相关系数显著为负,盈利因子RMW 与规模因子SMB、投资因子CMA 间的相关系数分别为-0.75 和-0.63,负相关性非常显著。综合来看,本文所选的8 个因子相关性较低,适合通过分散化投资降低风险,提高投资收益。

表3:因子相关系数矩阵
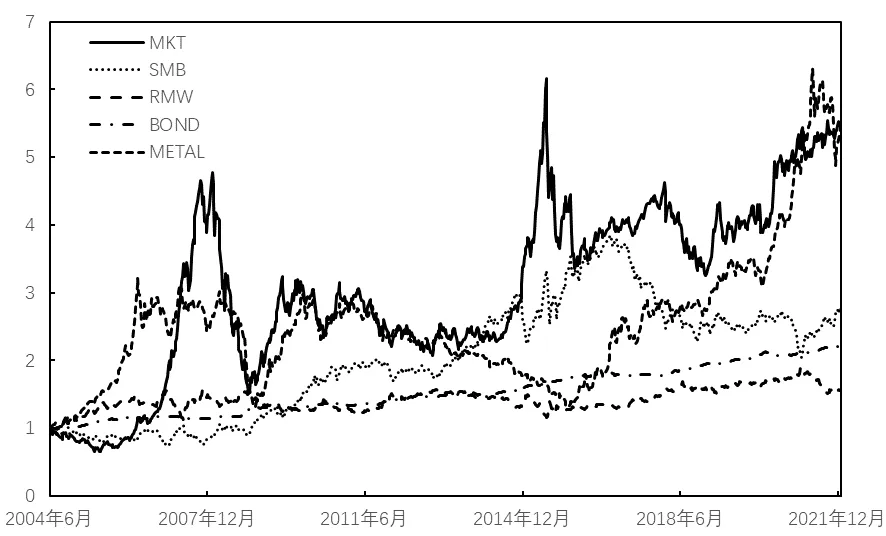
图3:因子净值曲线
(二)随机森林模型预测及变量重要性分析
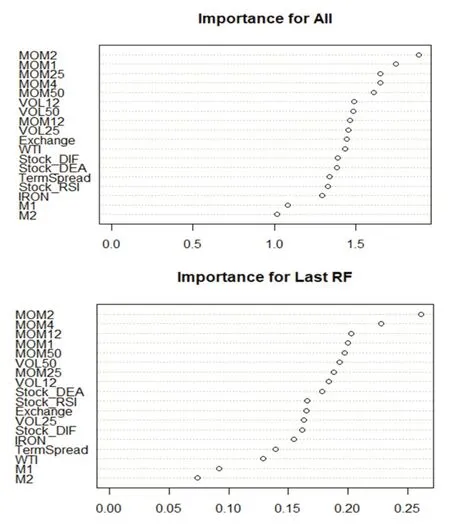
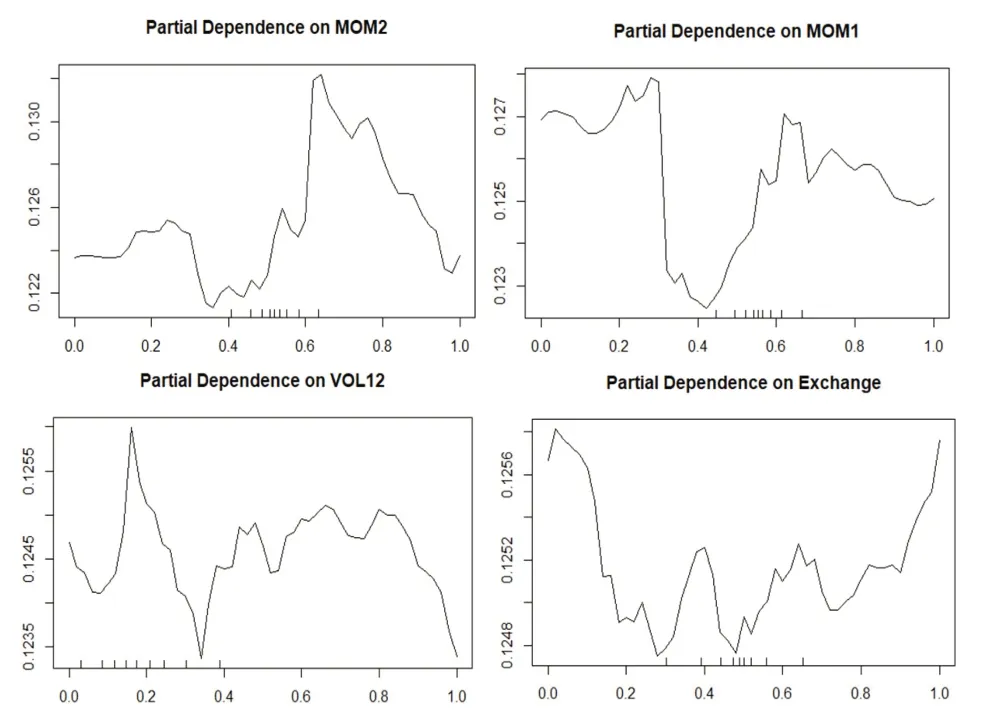
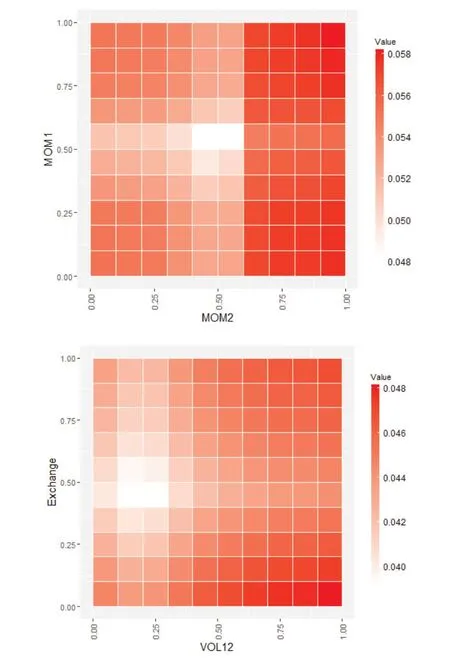
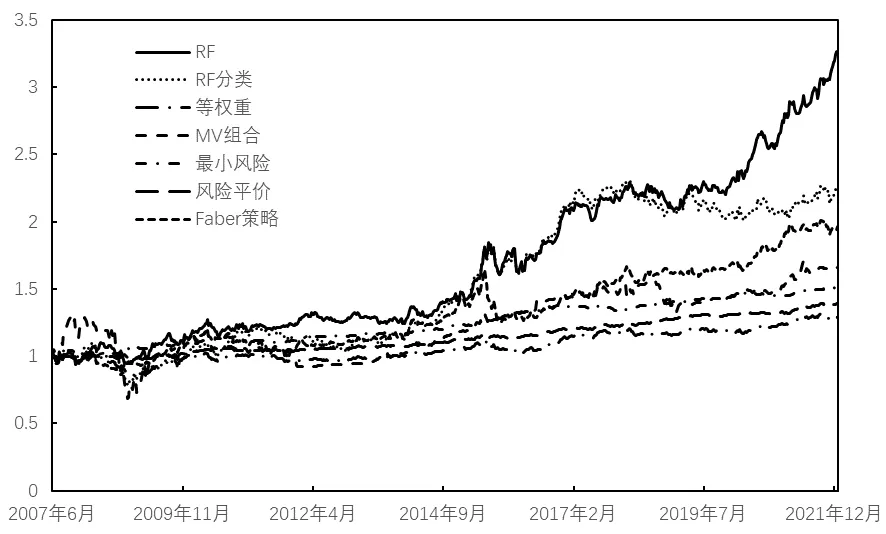
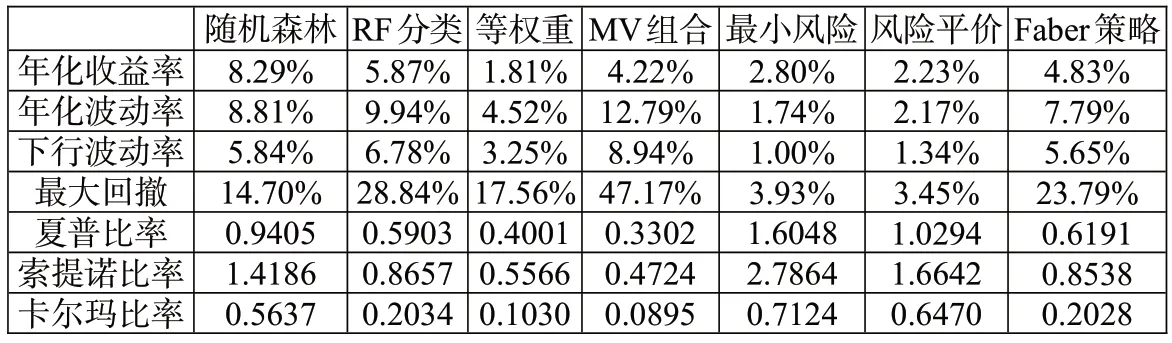
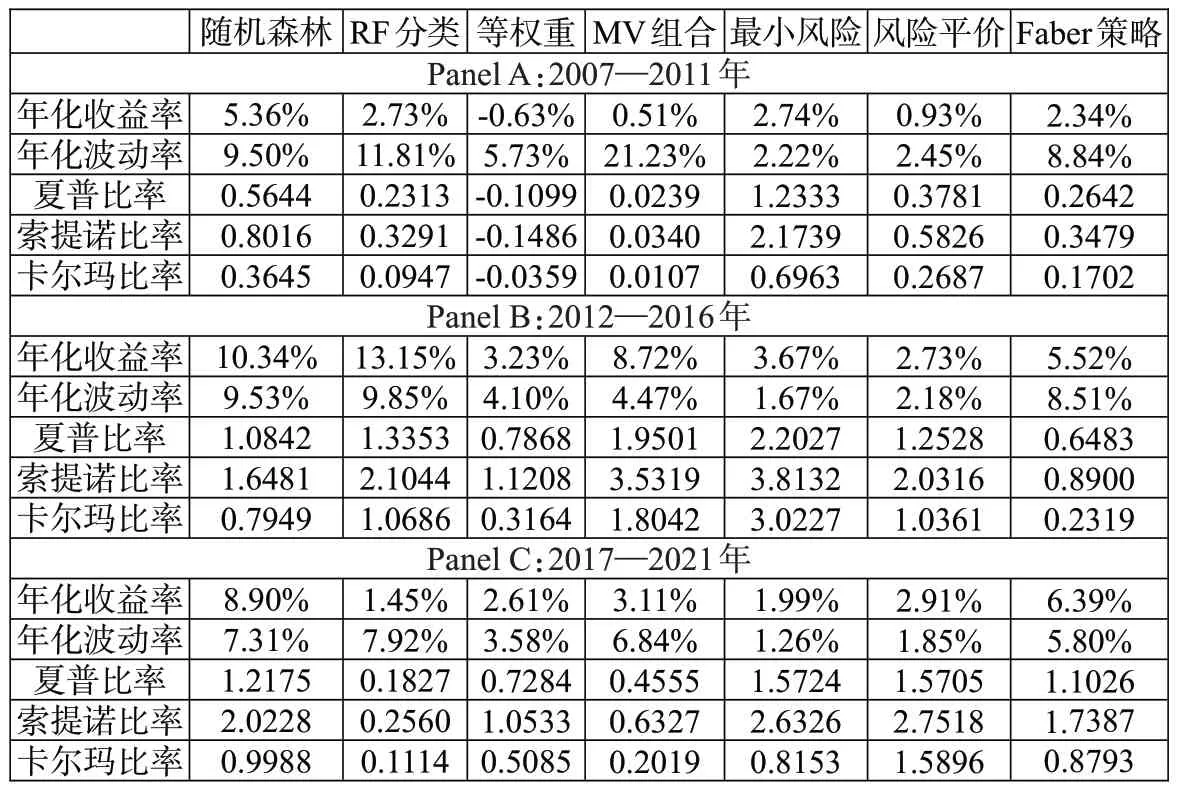
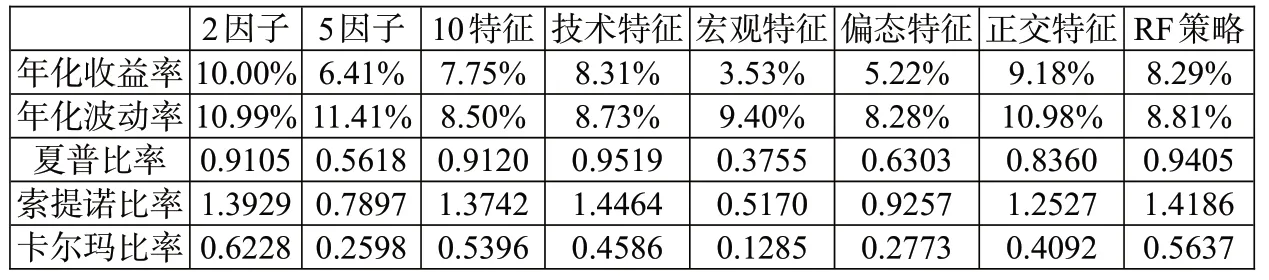
1.模型预测能力分析。我们利用缩尾及标准化处理后的特征值对同样经过缩尾和标准化处理后的因子收益率进行随机森林回归。具体而言,我们采用第t-250期至第t-1期的数据作为滚动训练样本,在训练样本中采用第h-1 期(t-249 表4:模型预测能力分析 2.特征重要性分析。机器学习模型最广受诟病的问题在于其“黑箱”属性,即无法知道特征与因变量之间的关系。随机森林模型可以通过基尼系数评估变量的相对重要性,相对于神经网络、支持向量机等其他机器学习算法,更像一个“白箱”。图4给出了本文的特征重要性研究结果,其中上图是将所有数据构造静态随机森林计算出的结果,下图是采用滚动方法构造随机森林,根据最后一个随机森林计算出的结果。通过整体和最后一个随机森林的对比,可以判断特征的相对重要程度以及特征重要性的变化。可以看到,在整体的分析结果中,动量指标起到了最重要的作用,其次是波动率指标,宏观指标的预测能力较弱;最后一个随机森林的分析结果中,动量指标和波动率指标的预测能力仍然是最强的,只是25 周波动率的预测能力有所降低,大部分宏观指标的预测能力仍然很弱。总体而言,虽然不同的随机森林中变量重要性并不完全一致,但是动量和波动率等量价指标的重要性相对更强,而宏观指标的作用微乎其微。 图4:特征重要性分析 机器学习模型的预测精度之所以远远好于普通的线性模型,除了其能输入大量特征而不会导致共线性外,更关键在于它能处理特征与因变量之间的非线性关系以及特征之间的交互作用。我们采用PDP 方法计算特征不同取值对预测能力的影响,并根据预测能力的改变程度评估特征的重要性以及影响的非线性;同时,我们还可以对不同特征同时进行赋值,从而观察特征间的交互影响。图5和图6报告了研究结果,其中图5是部分特征(选取了重要性较高的四个特征,包括动量、波动率及宏观特征)的特征依赖图,可以观察特征的非线性影响;图6是部分特征预测能力的热力图,可以观察特征间的交互作用。 1.非线性作用分析。从图5可以看到,所有特征的非线性都非常明显,如两周动量指标MOM2 取值在0.6附近时对因变量的预测能力最强,取值趋向于0或1 时预测能力较弱,取值在0.4 附近时预测能力最弱;一周动量指标MOM1 取值在0.4 附近时预测能力最弱,但是当取值趋向于0 时预测能力较强;十二周波动率指标VOL12 的预测能力波动较强,随着取值的升高,经历了几轮上涨再下跌的趋势;汇率Exchange 对因变量的影响则符合两端高、中间低的特征。综合来看,所有特征的非线性均非常明显,这也是机器学习模型预测能力普遍较强的原因之一。 图5:变量非线性影响分析 2.交互作用分析。图6中上图报告了一周动量指标MOM1 和两周动量指标MOM2 的交互作用,下图报告了十二周波动率VOL12 和汇率Exchange 的交互作用,颜色越深说明模型预测能力越强,变量越重要。从上图可以看到,当MOM2 取值较高、MOM1取值趋向于两端的时候,模型预测能力最强;当MOM2 取值较低、MOM1 取值趋向于两端的时候,模型预测能力较强;而在MOM1 和MOM2 取值都中等的时候,模型预测能力很弱。从下图可以看到,当VOL12取值较高、Exchange取值较低的时候,模型预测能力最强;当VOL12 和Exchange 取值均较高的时候,模型预测能力较强;在VOL12 取值较低、Exchange取值中等的时候,模型预测能力最差。综合来看,变量间的交互作用非常明显,机器学习模型对交互作用的识别同样是其预测能力强于线性模型的关键原因之一。 图6:变量间交互作用分析 除了利用预测误差来检验随机森林模型的预测能力外,我们还利用构造投资组合的非参数方法来对随机森林模型的有效性进行检验。具体而言,根据随机森林模型的滚动预测结果(滚动样本为100 周,即约2年的建模周期),每期选择表现最好的3个因子进行等权投资。作为对比,我们考虑了随机森林分类(以下简称RF分类)模型、等权重、均值—方差(MV组合)、最小风险、风险平价及Faber 策略等投资组合。其中RF 分类模型是对每个因子建立分类模型,配置概率最高的3 个因子;等权重组合是将8 个因子进行等权配置;均值—方差及最小风险组合采用马科维茨方法构造;风险平价组合是每期使8 个因子的风险贡献相一致的组合;Faber 策略是趋势投资组合,每期选择在120 周均线以上的资产进行等权投资(Faber,2007)。表5报告了不同投资组合的绩效表现,可以看到,随机森林模型的收益最高,达到了8.29%,虽然其波动率较高,但是最大回撤反而低于等权重、MV 和Faber 策略组合,较高的收益加上适当的风险水平,使得其风险调整后收益普遍高于其他策略;最小风险及风险平价组合的波动及回撤均较低,主要是因为这两个组合中债券因子的权重较高;RF 分类模型的收益率虽然相对于其他模型较优,但是远逊于RF 模型,可能的原因在于RF 分类模型相对于随机森林模型损失了过多信息。图7展示了各策略的净值曲线,因为在构建预测指标的时候用到了50 周的数据(1年),在建模的时候需要用到100 周的滚动样本(2年),因此,净值计算从2007年6月开始。可以看到,随机森林和RF 分类策略的净值高于其他策略,但是RF 分类策略的净值从2018年开始持续震荡,而随机森林策略的净值保持了持续上升趋势,最终达到3.25,远高于其他策略。 图7:策略净值曲线 表5:投资绩效分析 1.分阶段检验。我们先将样本时间段分为2007—2011年、2012—2016年和2017—2021年三个跨度大致相等的时间段,每段包含五年的交易时间,并分别统计不同时间段内各策略的投资绩效,结果如表6所示。可以看到,除了2012—2016年RF 分类策略的收益率略高于RF策略外,其他时间段RF策略的收益率均高于其他所有策略,且RF 策略的最大回撤在大部分时间内好于RF 分类、等权重、MV 及Faber 策略组合。因此,综合来看,前文的研究结论是稳健的,相对于其他策略,随机森林策略由于考虑了特征的非线性影响及交互作用,能够显著提高投资策略的绩效表现。 表6:分阶段稳健性检验 2.更改策略特征的稳健性检验。除了分阶段进行检验,我们还针对因子数量及变量特征进行了稳健性分析,表7报告了分析结果。其中,“2因子”是指选择每期仅选择表现最好的2 个因子进行等权配置;“5 因子”是仅利用市场因子MKT、规模因子SMB、盈利因子RMW、债券因子BOND、商品期货因子METAL 五个表现较好的因子,每期从中选择表现最好的2个因子进行配置;“10特征”是指从18个特征中选择重要性最强的10个特征建立随机森林模型,再滚动建模构造投资组合;“技术特征”指仅利用12 个技术特征进行建模;“宏观特征”指仅利用6个宏观经济指标进行建模;“偏态特征”指在18个特征的基础上,增加上行波动率、下行波动率、偏度和峰度(均包括25周和50周两个周期)特征进行建模;“正交特征”是指对18个特征进行施密特正交化后再进行建模。 表7:更改因子和特征的稳健性检验 可以看到,“2 因子”策略提高了策略收益率,但是波动率和最大回撤也有所增加,风险调整后收益略微不及原始的RF 策略,说明集中化投资对结果的影响并不大;“5因子”策略在降低收益的同时反而提高了风险,说明虽然其他3 个因子(HML、CMA 和UMD)整体投资收益不高,但是其阶段性表现可以提高整个策略的投资绩效。对特征进行筛选对投资绩效有一定影响,“10 特征”策略略微降低了投资风险,但是投资收益也出现了一定下滑;“技术特征”策略则在略微降低投资风险的同时,使收益发生了轻微上升,从而导致夏普比率从0.94 提高到0.95;宏观特征在随机森林模型中的重要性并不高,故“宏观特征”策略表现远差于原始随机森林策略;加入偏态特征因子是无效的,“偏态特征”策略的收益率反而大幅低于原始随机森林策略,说明向机器学习模型中加入过多的、效果不强的因子,并不能提高模型的预测能力;将特征进行正交化有助于提高收益,但是风险也随之升高,从风险调整后的收益来看,这样的操作得不偿失。综合来看,无论是改变因子的组合,还是对特征进行重新筛选,随机森林策略均能表现出较高的投资绩效,前文的研究结论是稳健的,而且在建模前进行一定的特征工程(如精选技术特征)对于进一步提高投资绩效可能是有帮助的。 机器学习模型能够有效解决变量间的共线性问题,处理变量间的非线性关系及交互影响,故其预测能力显著高于普通的线性模型。选取2004—2021年8个大类资产因子(包括股票市场的MKT、SMB、HML、RMW、CMA 和UMD 因子,债券市场的BOND 因子,商品期货市场的METAL 因子)以及18个量价及宏观特征,构造随机森林模型,考察了模型的预测能力、特征的重要性和影响,以及所构造投资组合的投资绩效。研究结果表明:第一,相较于普通OLS 及LASSO 模型,随机森林模型预测能力显著提高;第二,量价特征尤其是动量因子在随机森林模型中的重要性远高于宏观特征;第三,特征对因变量的影响是非线性的,且特征之间存在着显著的交互作用,这也是机器学习模型能够取得较好预测效果的重要原因;第四,随机森林模型构造的投资组合的投资绩效远好于常见的等权重、MV、最小风险、风险平价及趋势投资组合,也要好于RF 分类算法构造的投资组合;第五,研究结论在不同的样本期内均是稳健的,更改因子或特征的性质后的结果依然稳健,在建模前进行一定的特征工程(如精选技术特征)对于进一步提高投资绩效可能是有帮助的。 本文的研究结论是对投资组合理论以及人工智能理论的有益补充,对于投资实践也具有较强的借鉴意义。未来可以从以下方面进一步开展深入研究:首先,本文选择了8 个常见的大类资产因子,但是实际上发表在金融学期刊的因子成百上千(Harvey 等,2016),未来的研究可以选择更多、更为有效的因子进行配置,通过分散化投资的方法可以实现更稳健的收益;其次,正如本文稳健性检验中所发现的,对特征进行特征工程有利于提高投资绩效,未来可以尝试降维、降噪等更多方法进行先期的特征工程,使特征的提取及输入更有效,必将带来更高的投资绩效;再次,可以对所选因子进行更为有效的配置,而不是简单的等权重,如均值—方差优化、风险平价、尾部风险优化等方法均可以用来构造更稳健的组合;最后,本文研究的是因子配置,但是实际上,本文提出的8 个因子中,只有债券因子BOND 和商品期货因子METAL是可以直接投资的,6个股票类因子并非可以直接投资,因此,可以进一步研究如何利用可投资资产进行因子的投资和配置,代表性方法包括但不限于因子映射、组合优化等。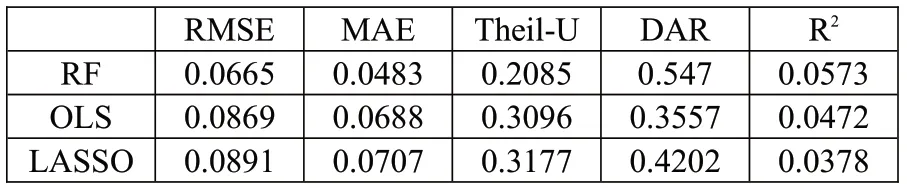
(三)变量非线性及交互作用分析
(四)投资绩效分析
(五)稳健性检验
四、结论与展望
