超声全聚焦成像中等声程线伪影剔除方法*

宋寿鹏 陈仪倩

(江苏大学机械工程学院 镇江 203022)

0 引言

基于超声全矩阵(Full matrix capture,FMC)数据的全聚焦成像算法(Total focus method,TFM)是近年来兴起的一种后处理成像技术[1-3]，广泛用于构件缺陷检测与成像中[4-6]。该成像技术可将待测区域进行全域聚焦，获取更加丰富的缺陷信息，成像效果也得到明显提升[7-10]。但该成像技术在全域声场解算中，由于超声旁瓣能量泄露以及等声程线扩散[11]，不可避免地会产生伪影现象，常通过变迹处理抑制旁瓣幅值[12]。而等声程线扩散产生的伪影成因与全聚焦成像原理相关，并不便于直接剔除，影响着缺陷的量化与评估[13-17]。若直接根据声场强度阈值剔除伪影，又会导致有效缺陷图像信息的丢失。因此，发现并剔除这类等声程扩散引起的原理性伪影具有重要的研究价值。

针对全聚焦成像伪影问题，国内外学者开展了广泛的研究。周正干等[13]针对双层介质中缺陷全聚焦成像时的伪影问题，提出了根据全聚焦能量指向性和扩散的图像修正方法，减小了近表面全聚焦成像时的能量误差，降低了伪影出现的可能性。贾乐成等[14]指出指向性函数可对单阵元声场能量进行较准确的校正，但全聚焦通过阵列不同收发模式下聚焦点幅值不断叠加成像，即便通过指向性函数进行校正也会出现失真，提出改进阵元指向性校正模型，并对全聚焦成像模型进行了修正，降低了伪缺陷出现的可能性，但成像时间成倍增加，后续通过三角矩阵数据的减少全聚焦成像时间。Potter 等[15]引入扩散场的概念，模拟超声信号在有界介质中不断地散射和反射，可以获取到均匀声场，并可反演出两点间格林函数时域结构对全聚焦成像算法进行后处理，降低了成像的噪声和伪影。杨贵德等[16]提出通过小波变换并结合无偏似然估计，对全聚焦成像信号进行滤波来达到降低伪影的目的。陈赛[17]预先设定强度阈值，统计该像素点回波大于该阈值时的数量来判别该点是否为伪影，若为伪影，就以周围像素加权平均来填充伪影部分，以达到减弱伪影的目的。

这些伪影去除方法大部分是通过对全矩阵数据进行校正后再进行缺陷成像，其去除伪影效果主要依靠于校正模型。由于校正模型的去伪影效果与传感器性能参数、声束入射角度和待测试块等参数有关，因此在不同的检测工况下，需要对校正模型进行重新计算，以达到去除伪影的效果，降低了算法的实用性，并且其计算时间成倍增加。而文献[17]提供的方法虽然不需考虑检测工况下模型的调整问题，可通过全矩阵数据统计具有特定回波幅值的声程线个数来判别伪影。但其回波阈值主要依据经验值，并且缺陷的分布和噪声量级等因素对该方法的影响较大，当缺陷个数较多时，该方法的伪影剔除效果下降。

针对这些问题，本文提出了一种新的伪影剔除方法，将传感器测量数据分为两路，一路用于全聚焦成像，一路用于等声程线判别。全聚焦成像算法采用常规的成像方法，其像作为剔除伪影的原始待处理图像；等声程线判别的目的是确定该等声程线是否为有效等声程线，判别依据为采集数据的均方根误差，可根据信号自适应计算得到。融合有效等声程线数量与图像强度分布特征，就可进行原始图像中伪影的辨识与剔除。伪影剔除后，将空缺部分用图像矩阵中强度最低像素值填充，即可获取剔除伪影后的缺陷图像。

1 超声全聚焦成像算法及其伪影分析

1.1 超声全聚焦成像原理

基于全矩阵数据的全聚焦成像算法是目前超声成像领域研究的热点之一，全矩阵数据是一种阵列传感器阵元数据采集方法，采用“一发全收”的模式，可以获取更加丰富的缺陷回波信息[7]。以线阵为例，假设阵元个数为1×N，当任一阵元发射结束后，全部阵元处于接收状态。若阵元i(1 ≤i≤N)为发射阵元，接收阵元j(1 ≤j≤N)接收到的回波为Sij(t)，依次激发所有阵元，全部阵元发射完毕后，可接收得到N ×N个A扫信号组成的数据矩阵S：

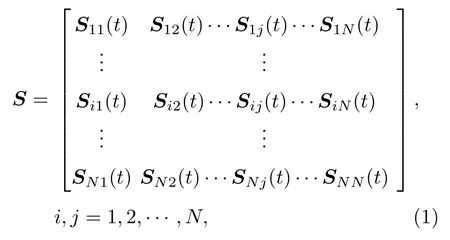
其中，Sij(t)表示第i号阵元发射、第j号阵元接收的数据。

全聚焦成像算法的核心思想就是利用全矩阵数据S获取每个空域聚焦点的叠加声强，按声强大小在聚焦点成像。设声发射方向截面上任意点P(xp,yp)处聚焦声场强度I(xp,yp)为

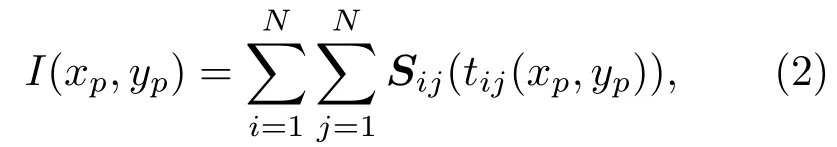
其中，

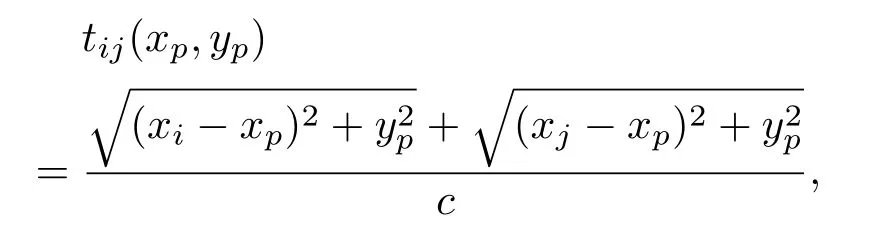
表示i号阵元(xi,0)发射，第j号阵元(xj,0)接收，聚焦点P(xp,yp)处的波达时刻；c为材料中的声速；截面xOy的坐标原点选为传感器阵列检测位置对应的阵列几何中心。

将I(xp,yp)按强度大小在截面上用色标表示，就可得到阵列在该检测位置对应的纵向截面上的声场聚焦分布图，进而获取全矩阵数据采集模式下该截面的全聚焦图像。

1.2 全聚焦成像时伪影成因分析

由全聚焦成像算法可知，当i号阵元发射、j号阵元接收时，在空间存在一系列点使得阵元发射信号声程与阵元接收信号声程和相等，将这些声程和相等的点连接起来，就形成了以i阵元和j阵元几何中心为焦点的椭圆，这些椭圆在试件形成的非闭合曲线就是等声程线。等声程线形成过程如图1所示。

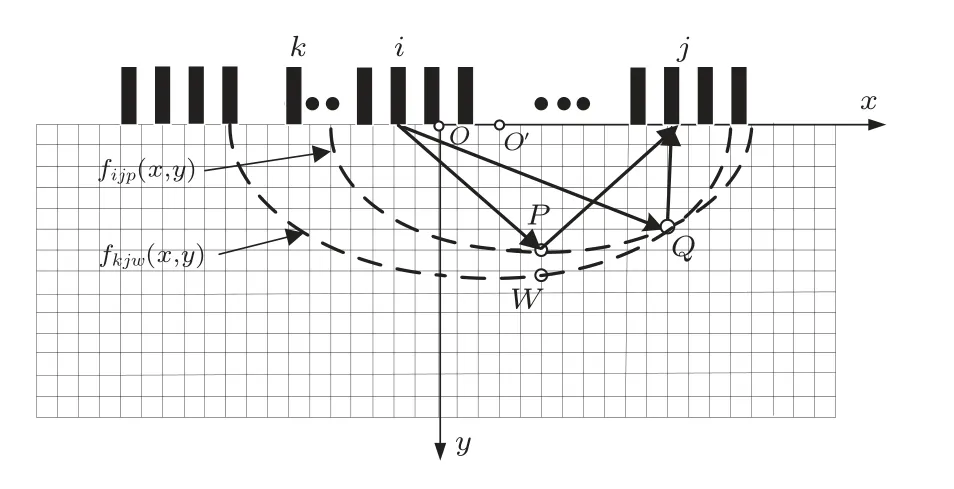
图1 等声程线形成示意图Fig.1 Isoacoustic contour formation schematic diagram

在相同的收发阵元模式下空域聚焦点P(xp,yp)和Q(xq,yq)到发射阵元i与接收阵元j的声程和相等，因此两点处于同一等声程线上。由于等声程线构成的椭圆焦点在xOy平面的x轴上，且椭圆圆心在其焦点的连线上，设椭圆圆心坐标O′为(A,0)，此时等声程线方程为

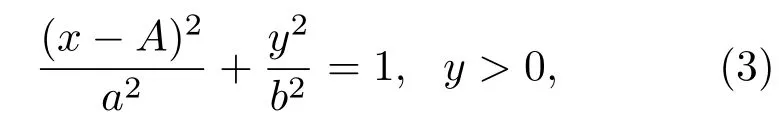
其中，a为椭圆的长半轴；b为椭圆的短半轴。设该椭圆的焦距为2dc，则当发射阵元i的坐标为(xi,0)、接收阵元j的坐标为(xj,0)时，2dc=|xj -xi|，圆心为，根据椭圆几何关系建立如下方程组：

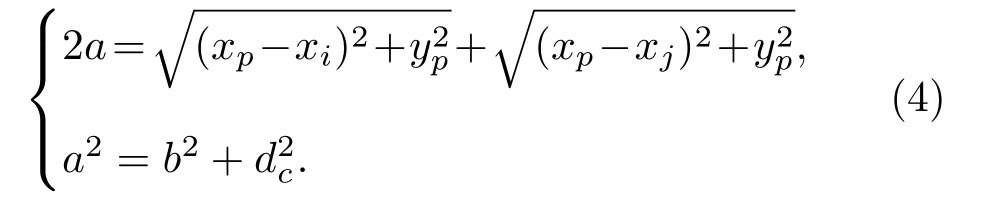
由式(4)解算出a2和b2，并代入式(3)可得到i号阵元发射、j号阵元接收时，P点的等声程线方程为

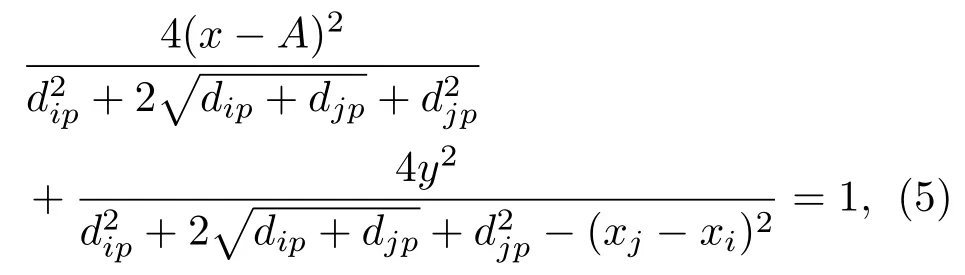
其中，

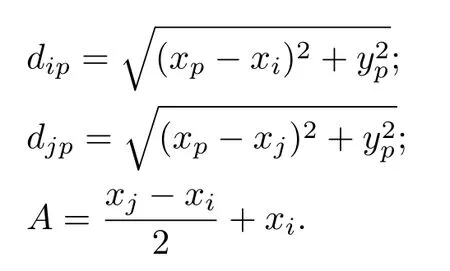
等声程线伪影的产生是由于等声程线扩散，在成像时虚拟点存在伪影叠加，即可造成伪缺陷影像。在图1 中，若在P点和W点处都存在缺陷，Q点处不存在缺陷，等声程线fijp(x,y)在P点和Q点具有相同的声场强度，同理等声程线fkjw(x,y)在W点和Q点也具有相同的声场强度，两等声程线都经过Q点，则Q点处的声强经过叠加之后加强。如果以声强分布成像，就会在Q点产生较强的伪影。考虑到目标体回波幅值在离表面较近时衰减小，所以近表面伪影现象会更严重，这也是为什么在近表面处伪影现象比其他区域更明显的原因。

2 有效等声程线判别及伪影剔除法则

在成像区域的每个聚焦点遍历全矩阵数据，可获得N×N条不同声强的等声程线。若P点存在缺陷，经过该点的等声程线叠加形成聚焦点合成声强，幅值增加显著。若Q不存在缺陷，等声程线同样会在该点产生叠加，如果信号回波中对应该点的信号幅值不为零，则声强也会加强，从而形成伪影。如果回波信号中有噪声，或者回波信号中存在拖尾现象，则伪影会更加明显。但Q点处较大声强的等声程线个数应明显少于P点。因此，如果能统计出所有聚焦点处特定强度ΔI的在同一空间聚焦点处的相交次数，就可以判别是否为伪影。将这些反映缺陷存在的等声程线称为有效等声程线。

当ΔI选择过大时，可能过滤掉缺陷回波；当ΔI选择过小时，则不足以判别出伪影。实际缺陷的尺寸和分布对缺陷回波幅值的影响较大，同时需考虑噪声的影响。均方根误差原则为统计学的一种方法，反映了估计量与被估计量之间差异程度，常用于阈值选取[18]。将全矩阵数据与均方根误差方法结合，可得有效等声程线阈值计算过程如下：

假设通过希尔伯特变换得到回波信号Sij(t)的包络为(t)：

求取包络峰值最小峰值I′ij，并存储在矩阵I′中，得到

其中，I′ij代表第i号阵元发射、第j号阵元接收的回波信号的最小峰值。

为了减少噪声的影响， 计算的平均值Mean()：

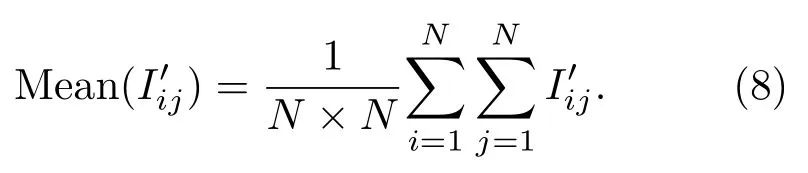
将小于Mean(I′ij)的I′ij依次放入集合C1，大于Mean(I′ij)的I′ij依次放入集合C2，则可计算得到两个集合C1和C2的标准差分别为δ1和δ2：

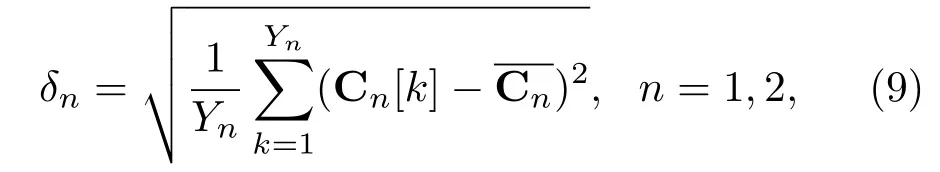
其中，Yn表示集合Cn中的数据个数。Cn[k]为集合Cn第k个值为集合Cn的平均值。

令有效等声程线阈值ΔI为

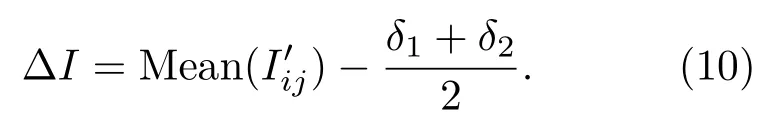
当某等声程线对应的声强大于ΔI时，该等声程线即为有效声程线，并将成像截面离散成有限面积的聚焦微元，微元的大小以每个发射阵元信号只经过一次微元而设定，实际上也就确定了等声程线的间隔。则传感器阵元发射和接收遍历后，微元中经过的有效等声程线个数即为有效等声程线相交数目。

一般情况下缺陷点处的有效等声程线相交线数量要明显多于伪影处，但当缺陷个数较多或回波信号信噪比(Signal-noise ratio,SNR)低时，伪影对应微元处的有效声程线相交数目可能与缺陷微元处的接近。如果此时直接根据相交数量的多少判定伪影和缺陷，误判的概率就会增加。因此通过有效声程线相交数目判别后，采用原始图像的强度进行二次判别，以达到更完善的剔除伪影效果。其具体流程图如图2所示。

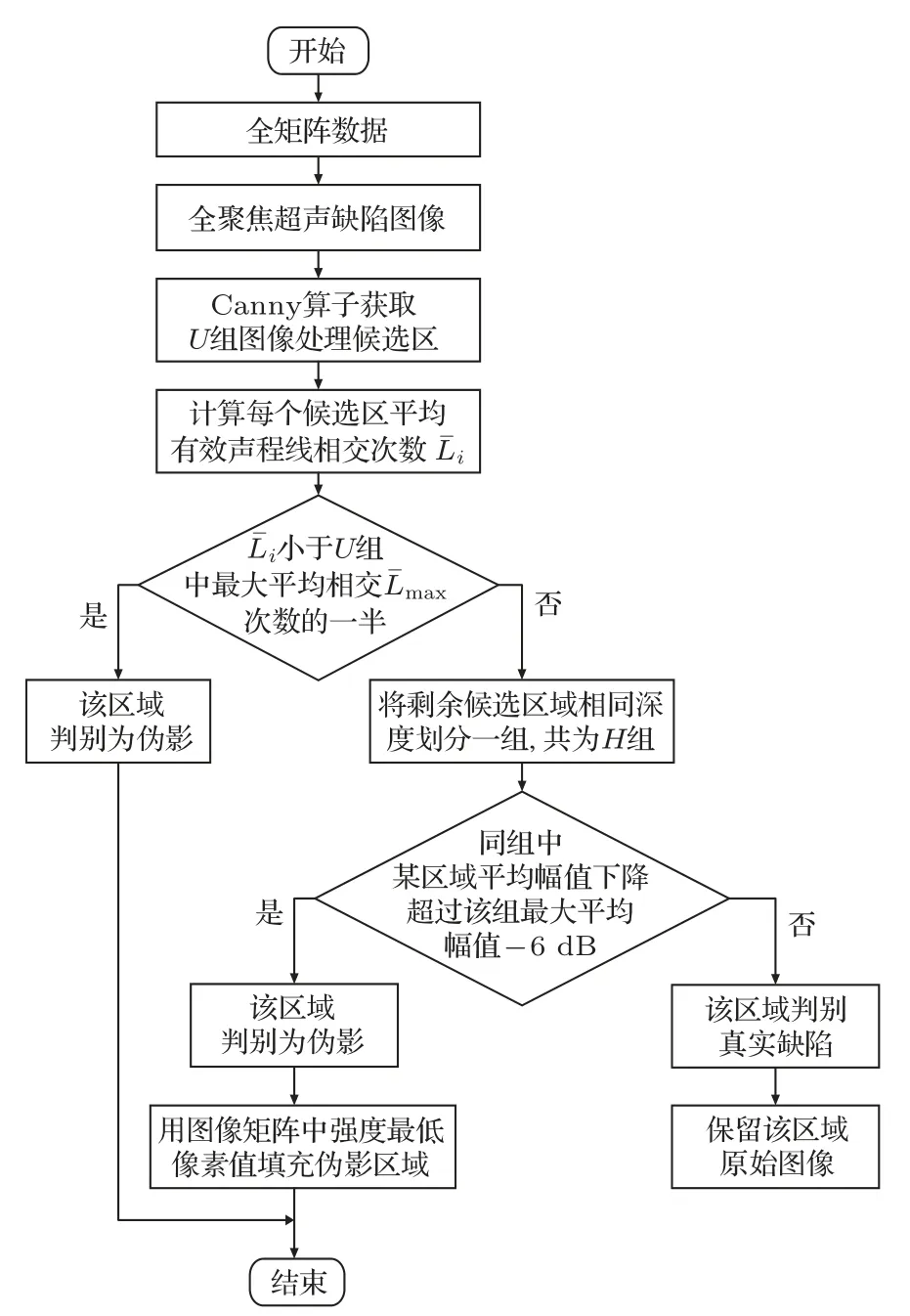
图2 全聚焦成像伪影剔除流程图Fig.2 Flow chart of artifact removal in all-focus imaging

为了初步判定伪影区域，避免全局搜索，通过提取成像图中缺陷和伪影的边缘获得成像图中的处理候选区域。Canny 边缘检测方法以其低错误率、最优定位和单边缘性3 大优势，被认为是最成功的边缘检测方法之一[19]。利用Canny 算子获取图像处理候选区边缘。并将这些区域拟合为U组矩形图像处理候选区域。比较所有区域的平均有效声程线相交数目，即该区域中平均每个微元的等声程线相交数目。当某区域的平均有效声程线相交数目小于U组候选区域中最大平均相交次数的一半时，认定该区域为伪影区域[17]。需要注意的是声程差别导致的声能衰减，因而原始图像在不同深度的缺陷处，其图像强度仍存在较大差别。因此需将各区域分组比较，划分准则是将被测试件同一深度的区域作为一组，若候选区域相交也认定为同一组，即可将U个候选区域划分为O组(1 ≤O≤U)，每组H(1 ≤O≤U)个。由于目前常用的阵列性能指标(Array performance indicator,API)需计算图像中从幅值最大值下降到-6 dB 之内的所有像素点的面积对成像质量做出评判[11]，因此通过候选区域内同一组内图像的强度-6 dB 值作为判断依据，认定此组内存在某区域平均幅值下降到该组最大平均幅值的-6 dB 以下时为伪影，以达到进一步剔除伪影的目的。

3 仿真试验

为了验证上述方法的有效性，选取直径通孔类和槽类标准缺陷试块在Field II 平台进行声场仿真试验，试块及缺陷几何分布如图3 所示，试块I为直线槽缺陷试块，其中缺陷1#的尺寸为5 mm×3 mm×2 mm，试块II 为横通孔缺陷试块，其中缺陷2#、3#、4#、5#直径均为1 mm。选用1×16的超声线阵，阵元的中心频率为4 MHz，阵元中心距为1.0 mm，阵元长度为10 mm，阵元间距为0.1 mm。待检测试块为钢材料，声速为5900 m/s，成像区域微元大小设置为0.1 mm×0.1 mm，成像幅值以分贝值表示，范围为[0 dB,-20 dB]。

对仿真环境和阵列各参数进行初始化设置后，即可获取当前检测环境下的全矩阵数据，本文共可获得16×16 个A 扫信号组成的全矩阵数据。以图3(b)的试块为例，当阵元激励为加汉宁窗的正弦信号时，其波形如图4(a)所示；本文仿真采样频率为100 MHz，每个A 扫信号有903 个采样点，任取全矩阵中单路回波A扫信号如图4(b)所示。

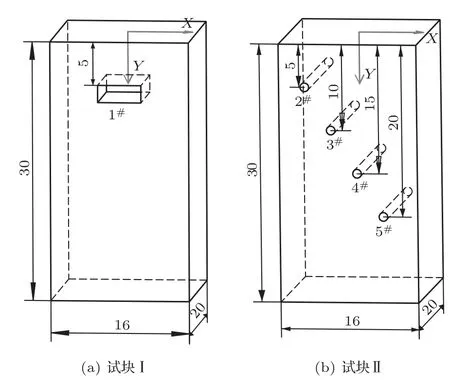
图3 试块缺陷分布示意图Fig.3 Defect distribution diagram of test block

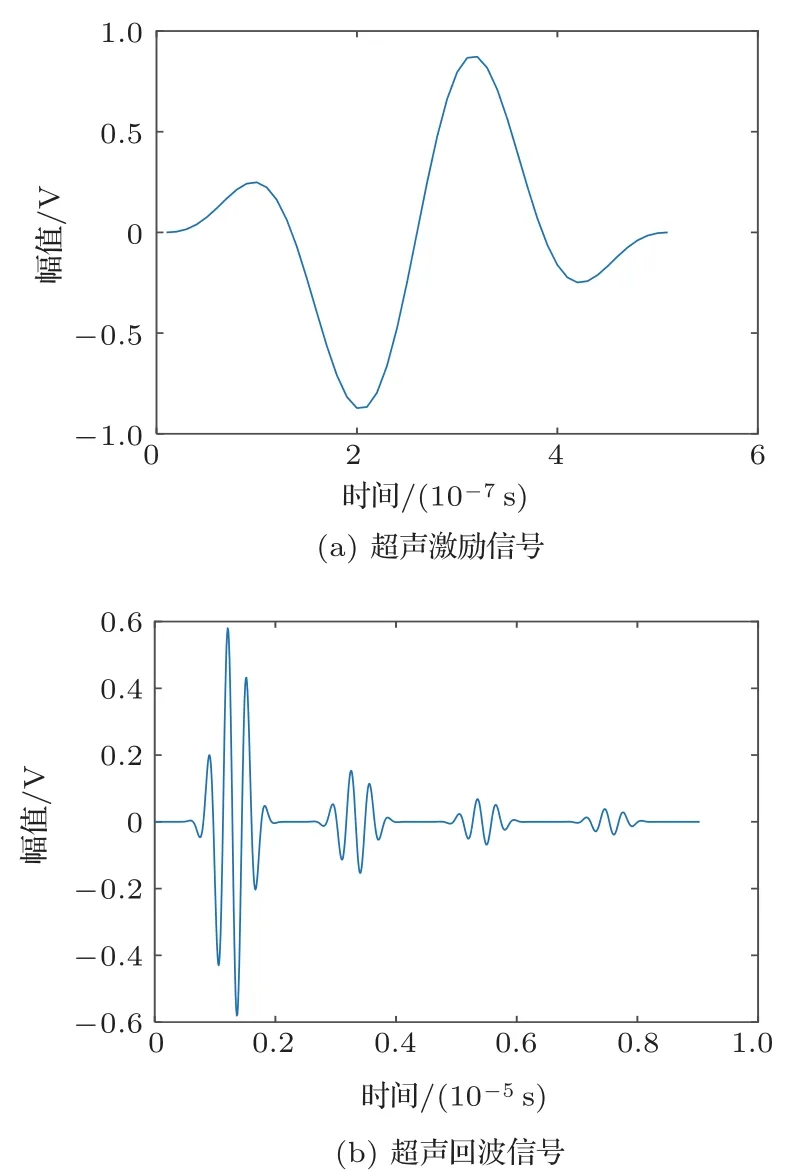
图4 仿真波形Fig.4 Simulation waveform

获取全矩阵数据后设置成像区域聚焦点微元大小，根据第1 节全聚焦成像原理，可求得所有聚焦点最终声场强度。不同缺陷的TFM原始图像如图5所示，成像幅值以分贝值表示，可看出在近表面缺陷处由于等声程线叠加产生的伪影现象明显。

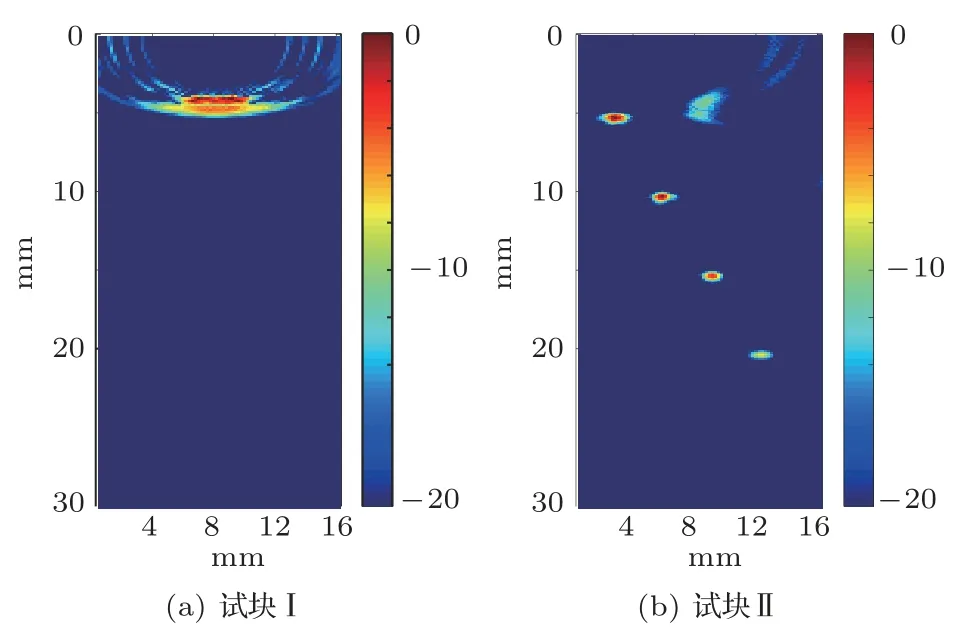
图5 不同试块原始TFM 成像效果Fig.5 Original TFM imaging effect of different block

利用Canny 算子从原始全聚焦图像提取候选区域，结果如图6所示。

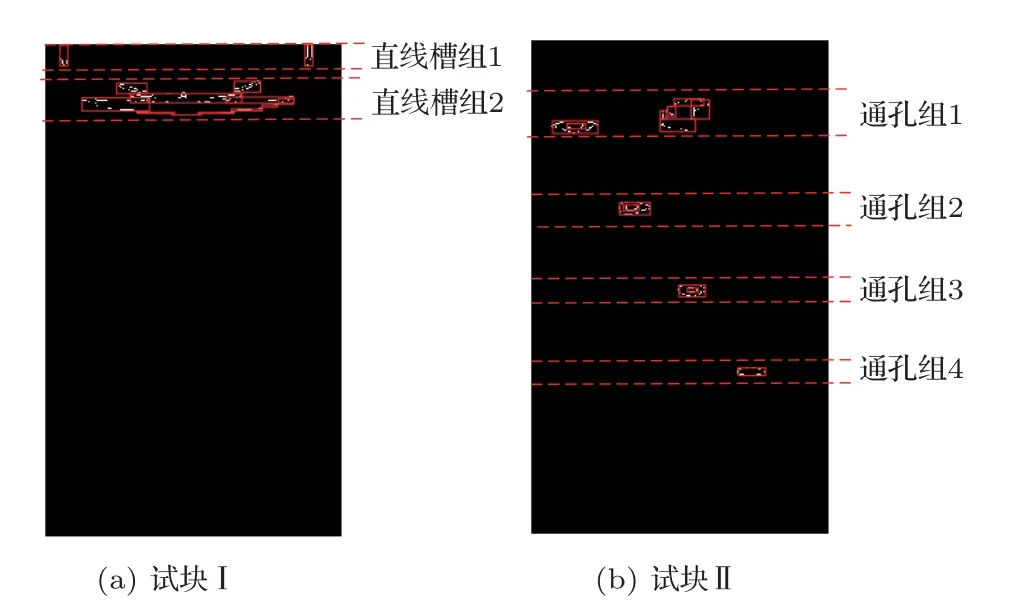
图6 Canny 算子提取图像处理候选区域Fig.6 Canny operator extracts candidate regions for image processing

对提取的区域进行分组，有直线槽缺陷的试块的图像候选区域可分为2 组，有通孔类缺陷的试块的图像候选区域可分为4 组，如图6所示。对于各组中不同区域的平均声强相差不大部分，无法直接通过图像强度判别是否为伪影，可通过有效等声程线相交个数来判定是否为伪影；对于各组中不同区域的平均声强相差-6 dB 的部分，可用声强分布和有效等声程线相交数目同时判定规则直接对伪影进行识别，进而达到剔除伪影的目的。通过以上伪影剔除法则对图5不同缺陷TFM图像进行处理，结果如图7 所示，表明论文中提出的方法将等声程线产生的伪影进行了有效剔除。

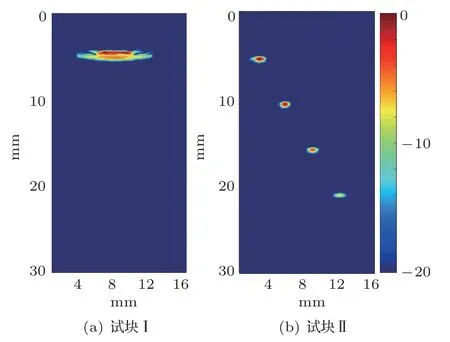
图7 不同缺陷剔除伪影效果图Fig.7 Comparison of effects before and after removing artifacts from different defects

为度量缺陷的量化精度，统计各图像候选区不小于该区域最大幅值6 dB 的像素面积大小，并将其与仿真试块模型中的缺陷大小进行对比，可得到成像的量化误差ΔH：

其中，S′和S分别为成像图像中缺陷面积和仿真模型中的缺陷面积。由式(11)可求得直线槽缺陷TFM 成像的量化误差为21.3%，去伪影后的量化误差为17.5%；横通孔缺陷的TFM成像的平均量化误差为26.3%，去伪影后的平均量化误差为21.5%。

为了验证不同大小缺陷成像的去伪影效果，在图3(b)的基础上改变通孔直径，设置多个不同直径的通孔缺陷试块，其参数如表1所示。

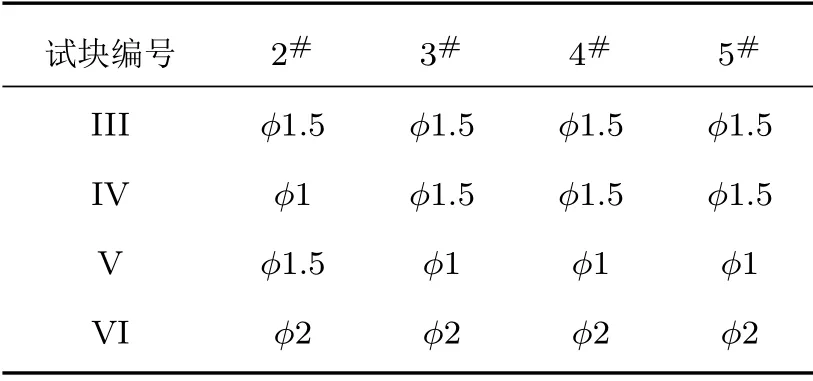
表1 仿真试验横通孔缺陷参数设置Table 1 Defect parameter setting of horizontal through hole in simulation test(单位: mm)

每个试块不同大小的通孔类缺陷成像效果如图8 所示，通过与TFM 成像图对比，可以发现其伪影剔除效果均得到明显改善。4个试块的TFM成像的平均量化误差为21.3%，去伪影后的平均量化误差为16.9%。

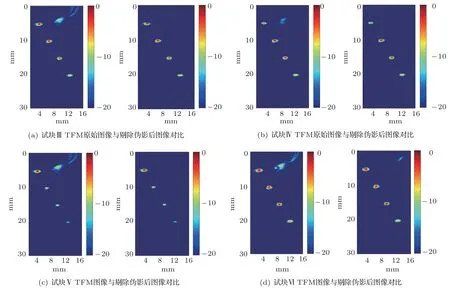
图8 不同试块通孔缺陷成像效果对比Fig.8 Comparison of imaging effects of through-hole defects in different test blocks

为了分析该方法在噪声条件下的鲁棒性，更贴近实际信号，在试块III的全矩阵中回波信号中分别加入不同强度的高斯白噪声。

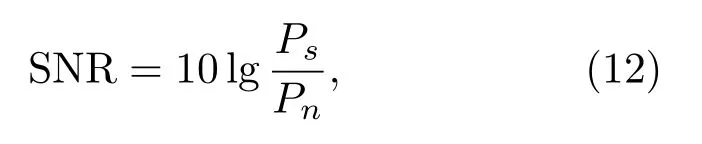
其中，Ps和Pn分别为信号和噪声的有效功率。文中分别对SNR 为15 dB、20 dB、25 dB 的噪声环境下进行了TFM 成像，并与剔除伪影后的效果进行了对比，结果如图9所示。

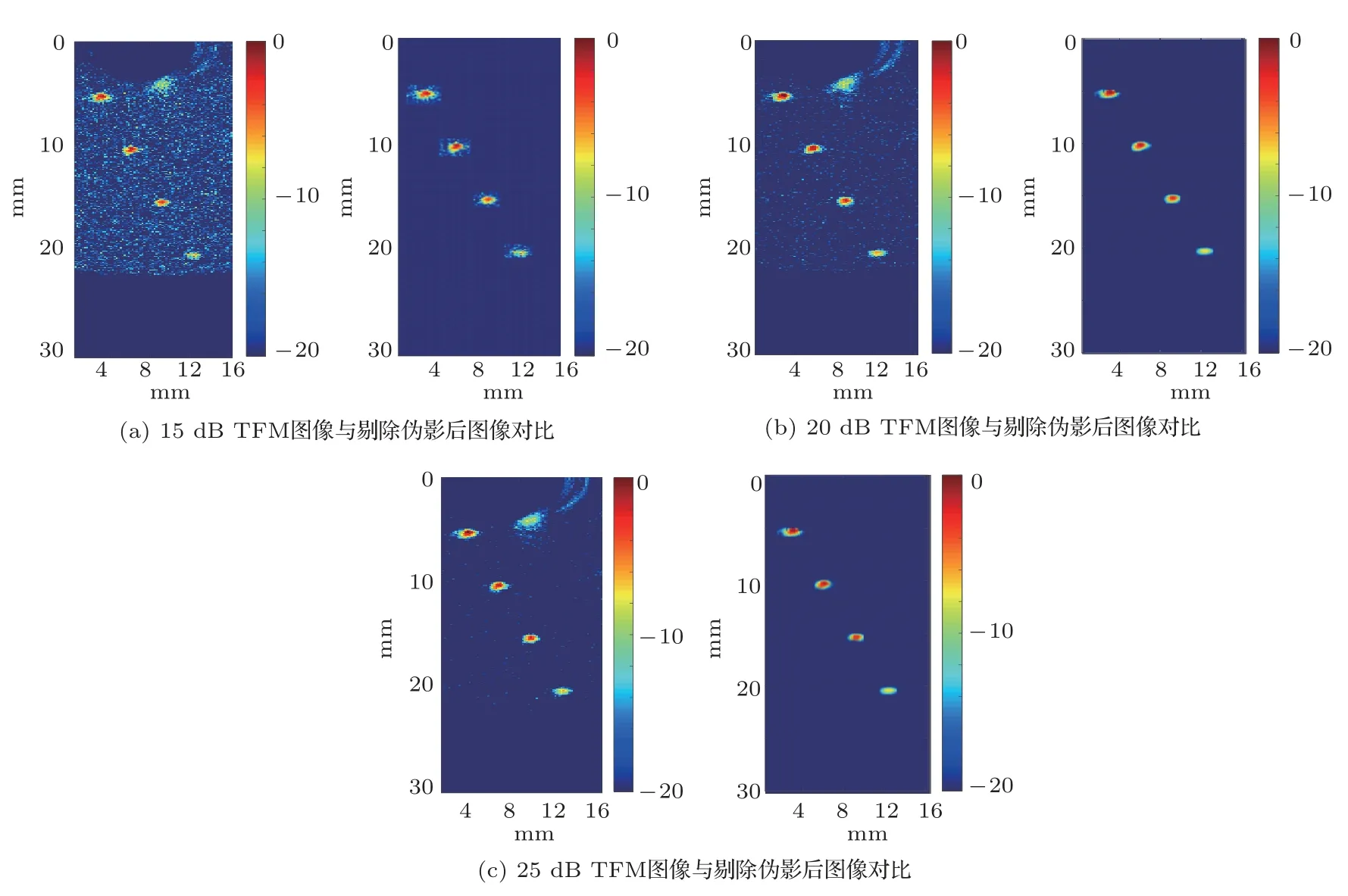
图9 不同SNR 下成像效果对比Fig.9 Comparison of imaging results under different SNR

可以看出，当SNR 高于15 dB 时，其噪声和伪影大部分被抑制。3种不同SNR下试块1的TFM成像的平均量化误差分别为35.6%，去伪影后的平均量化误差为分别为22.9%。

4 结论

在分析全聚焦成像算法中伪影产生原理的基础上，建立了全聚焦模式下等声程线扩散模型，并根据均方根误差原则判别有效等声程线。引入Canny算法获取全聚焦图像中的处理候选区域，结合有效等声程线数量与图像强度分布特征对原始图像中伪影进行辨识与剔除。通过对不同种类、不同大小缺陷在不同SNR下的仿真成像效果进行分析，结果表明：该方法可以有效剔除由于等声程线产生的伪影，尤其是近表面伪影去除效果更加明显，剔除伪影后缺陷图像的量化精度也得到了提高。由于Field II 平台的建模能力有限，本文只对单一介质中的形状规则缺陷进行仿真验证，后续可考虑通过有限元仿真分析本文去伪影方法对形状不规则缺陷以及复合材料中的去伪影效果。