随机多项式展开多特征向量约束-匹配场声源定位算法*
2022-09-16王翰卓李风华
王翰卓 李风华
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
自适应匹配场声源定位算法的加权向量由拷贝场向量和实验数据互谱矩阵联合得到。与传统线性匹配器相比,自适应匹配场定位方法具有对旁瓣更好的抑制能力。但自适应声源定位算法在实际应用中难以达到理想性能,主要原因有:(1)算法对水文环境参数失配和水听器位置误差比较敏感;(2)目标运动和水文环境的非平稳性导致的相干信号拍数的不足,难以获得真实的数据互谱矩阵;(3)水面强干扰以及定位二维网格空间划分过于稀疏将降低定位的准确率[1]。环境的失配是主导因素之一,因而,寻找耐受环境失配的声源定位算法是匹配场定位研究的重点。对此,研究者们对应开发了环境宽容匹配场处理器[2-5]、最优不确定场处理器[6-7]、降阶自适应匹配场处理器[8]、基于扇区特征向量约束的匹配场处理器[9-10]等。以上耐受环境失配的声源定位算法通常需要使用蒙特卡洛统计方法对随机或不确知的声传播环境参数进行反复抽样后计算拷贝声场。如上述环境扰动约束的匹配场处理器需要对随机或不确知环境下拷贝场复声压的互谱矩阵进行估计,最优不确定场处理器在求取关于声源位置的贝叶斯边缘后验概率密度时需要进行蒙特卡洛积分。针对二维空间声源定位,在空间网格划分完成后,依次假设声源位于其中的某个网格点上求取匹配器的输出。当定位网格点划分较稠密时,算法是比较耗时的。
为了克服蒙特卡洛统计方法计算量大、耗时高的问题,学者们提出了系列蒙特卡洛统计的代理方法,其中有代表性的为声场位移法[11-13]和随机多项式展开法[14]。其中随机多项式展开法由于其通用性较广泛受到部分研究者的青睐。随机多项式展开法将参数为随机变量的微分方程的解表示成以相互正交的随机多项式为基底的级数形式,随机多项式基底是方程中随机参数的函数。随机多项式展开方法提供了一种由输入端(方程参数)到输出端(方程解)的解析表达式,方便了有关方程输入参数的随机性在输出量中传递性的研究。对于方程解中随机多项式展开系数的求解,有基于盖辽金投影的嵌入型方法[14-15]和基于联合最小角度回归[16]、概率配点[17]、随机响应面[18-20]等一系列非嵌入型方法。近些年来,随机多项式展开方法被应用到环境参数随机或不确知时不确定声场的计算中:文献[21-24]使用Karhunen Loève展开[25]描述了水体声速水平方向的扰动量,使用嵌入随机多项式的抛物方程计算了声强均值、方差和复声压的水平互相关等统计量。通过与蒙特卡洛统计结果的比较,证实了该方法的准确性和高效性。相同近似误差下,声速起伏强度越强、复声压统计矩阶次越高时,复声压需要的展开截断幂次越高;文献[26]结合微分形式的单向耦合简正波声场计算模型,将各号模态的相位表示为随机多项式展开的形式。相比于直接将模态复幅度表示为随机多项式展开的方法,其使用较低的展开截断幂次即可获得准确的声场统计结果。文献[27-31]在浅海声源深度、潮汐、初始温跃层结构、沉积层声速等存在多种随机或不确定因素时,使用拉丁超立方抽样采集训练样本,以多元线性回归求解了复声压的随机多项式展开系数。在此基础上,计算了声强均值、方差和概率密度,并进行了敏感性分析。结果证实了环境存在多类型随机和不确知参数时随机多项式展开法的高效性和准确性;文献[32-34]使用海洋动力学模型模拟了海水声速的时空变化,引入深度上的经验正交函数降低海水声速不确定参数维度,使用随机多项式展开方法预报了声传播损失的概率密度并进行了实验验证。
因此,利用随机多项式展开表示环境随机或不确知时的不确定声场,可以快速计算拷贝场复声压的互谱矩阵,从而提高环境宽容匹配场声源定位算法的计算效率。如文献[35]利用随机多项式展开进行了不确知海洋中环境宽容的贝叶斯波束形成,在实验中实现了浅海不确定场中声源位置的定位。本文将以环境宽容的匹配场声源定位算法为例,讨论受内波、湍流等因素影响,浅海水体声速存在起伏的情况下,使用随机多项式展开表示拷贝场随机复声压、并估计其互谱矩阵时定位算法的性能表现。仿真讨论了输入为单拍、不同信噪比下算法的定位准确率和输出峰均比,比较了蒙特卡洛统计和随机多项式展开估计拷贝场声压互谱矩阵的计算耗时。结果表明,在浅海海水深度-声速剖面为负梯度且声传播路径上的二维声速存在起伏的环境中,在低频、水平声传播一定距离内,随机多项式展开法可以准确估计垂直阵接收声压的互谱矩阵,且计算效率较蒙特卡洛统计方法提高十倍以上;多特征向量约束的最小方差匹配场处理器可以实现比线性匹配器和最小方差无失真匹配器更高的定位准确率和输出模糊度峰均比。
1 随机多项式展开多特征向量约束匹配器
假设二维柱坐标系中,r是声传播水平方向的坐标,z是海水深度方向的坐标。c(r,z,ξ)是线性内波扰动下声传播路径上的海水声速,其中矢量ξ= [ξ1,ξ2,··· ,ξL],ξ中的元素为相互独立且服从标准正态分布的随机变量。二维声传播路径上的海水声速表示为平均声速¯c(z)与扰动量δc(r,z,ξ)之和:
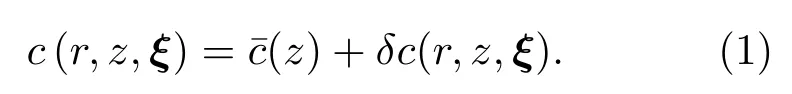
在深度上只保留第一阶经验正交函数[36]时,采用Karhunen Loève展开[25]表示声速扰动量为
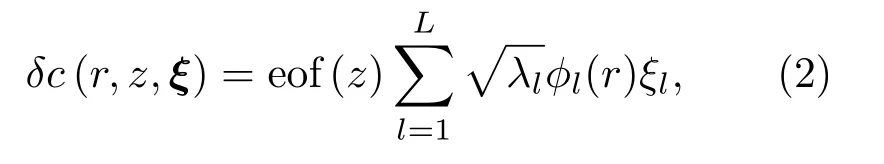
其中, eof(z)为海水声速的主经验正交函数;λ1,λ2,··· ,λL为经验正交函数展开系数的Karhunen Loève 展开特征值,L为展开项数;φ1(r),φ2(r),··· ,φL(r)为展开基。
本文采用了结合宽角抛物方程的嵌入型方法[21,24]计算频域复声压的随机多项式展开系数。假设某频点空间位置(r,z)处复声压P(r,z,ξ)的随机多项式展开为
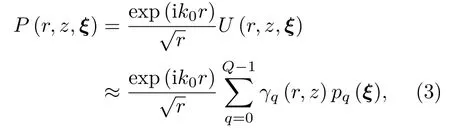
其中,k0为参考波数;U(r,z,ξ)为复声压的包络;{pq(ξ)q=0,1,···,Q-1}为展开基底函数集合,函数自变量为描述海水声速起伏的随机变量;γ0(r,z),γ1(r,z),··· ,γQ-1(r,z)为展开系数,其自变量为位置坐标;Q为随机多项式的展开项数,L为独立随机变量的个数,N为展开的截断幂次,三者关系为Q=(L+N)!/L!/N!。
由于随机变量为高斯型随机变量,展开基对应为埃尔米特多项式,当随机变量的个数L=2、展开截断幂次N= 2 时,埃尔米特随机多项式的函数形式如表1所示。

表1 埃尔米特随机多项式的函数形式Table 1 Hermite polynomials
随机多项式展开基在概率空间上相互正交,
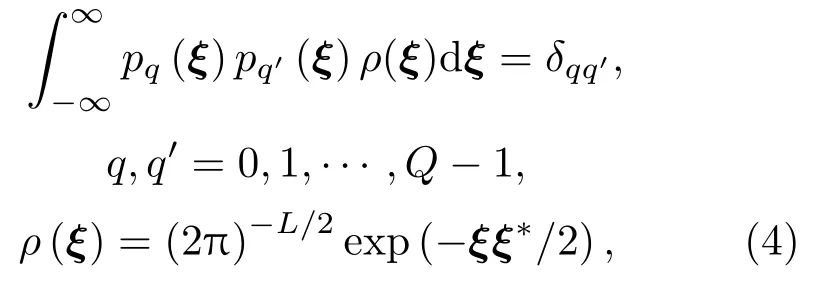
其中,ρ(ξ)为高斯型独立随机变量的联合概率密度函数,δqq′为Kronecker函数。
对于随机多项式展开基的具体构造方法及其性质,读者可参考文献[14]。
在宽角声学抛物方程中, 复声压的包络U(r,z,ξ)满足方程
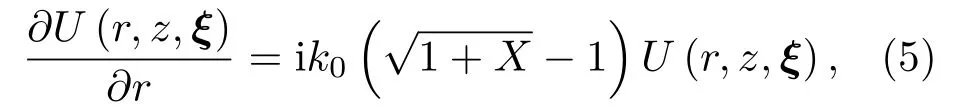
其中,算子X在声速存在随机扰动时近似为
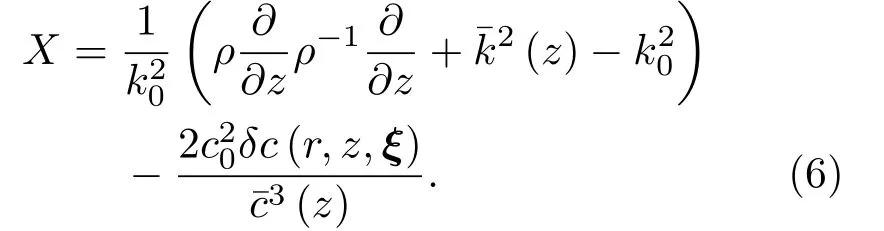
将式(6)代入到声学宽角抛物方程(5)中,并使用Padé近似[37]表示式(5)中的宽角抛物方程算子。
之后,将复声压包络的随机多项式展开级数式(3)代入式(5)中,使用盖辽金投影,对式(5)式两端依次乘上p0(ξ),p1(ξ),··· ,pQ-1(ξ)并作期望。投影保证了复声压包络的展开误差正交于随机多项式基底张成的函数空间。计算结果得到位置(r,z)处, 复声压包络展开系数γ0(r,z),γ1(r,z),··· ,γQ-1(r,z)的Q个耦合微分方程组,结合RAM模型的数值方法可对之求解[37-38]。
假设声源的真实位置为(rs,zs),固定位置的水听器阵列接收声信号某频点的复声压列向量为P(rs,zs,ξ),复声压互谱矩阵Re(rs,zs)定义为
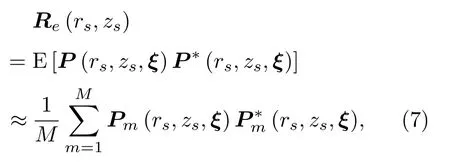
等式最右端为使用M拍实验数据对声压互谱矩阵的估计,Pm(rs,zs,ξ)代表第m拍的拷贝场复声压向量,其中上标*代表共轭转置。
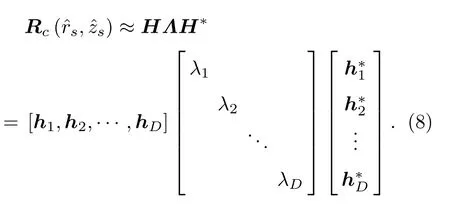
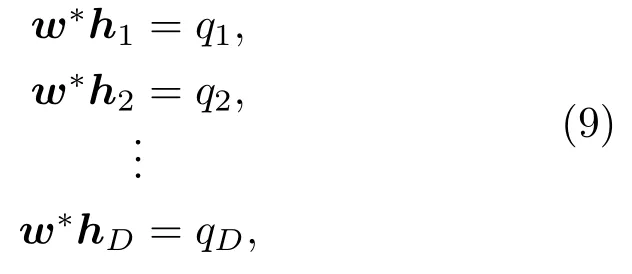
其中,q1,q2,··· ,qD代表各约束点的期望响应。问题转化为优化式(10)中的函数,其中c1,c2,··· ,cD为拉格朗日乘子。
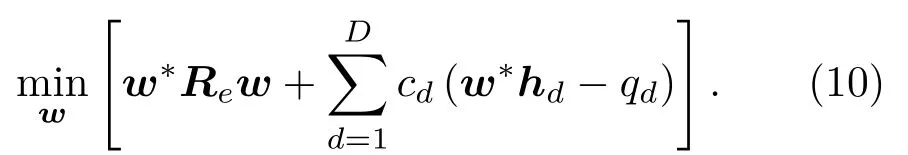
定义期望响应向量q= [q1,q2,··· ,qD]T,求解式(10)得到匹配器的加权向量为
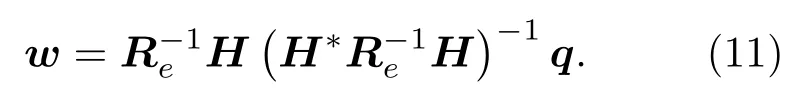
对应匹配器输出归一化后的平面模糊度函数为
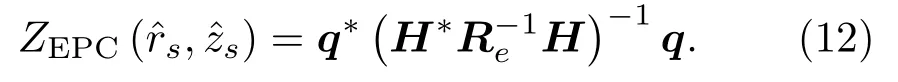
期望响应向量q的选择决定了匹配器的定位准确率和输出增益。通常期望响应向量的选择有最大化平均的空间白噪声增益和最大化最小的空间白噪声增益两类[5]。假设静态加权向量为wq,前者使得匹配器输出增益

最大,对应wq=h1,对应q=[1,0,··· ,0]T;后者选择静态加权向量以获得最差最优增益

且wq*wq= 1。式(14)意味着在声速随机变量ξ的所有的抽样中,选择wq使其最小的输出增益最大化。该方法没有显式形式的静态加权向量解。
由于对匹配器的定位准确率、输出峰均比的评价定义在声速随机变量集平均意义上,且为了最大化发挥随机多项式展开方法对匹配场算法效率的提升,本文研究选择最大化平均的空间白噪声增益下的期望响应,即q=[1,0,··· ,0]T。
上述算法需要对二维空间划分的每个网格点上对拷贝场复声压互谱矩阵进行估计。在一定条件下,随机多项式展开方法可以替代蒙特卡洛统计方法,更高效地估计互谱矩阵。蒙特卡洛统计方法如式(7),需要多次抽样生成声传播路径上随机的海水声速,并计算阵列位置处复声压的互谱矩阵。式(7)中,当抽样次数M足够多时,声压互谱矩阵的统计估计值将接近真实值,估计误差的收敛速度正比于M-1/2,即抽样次数的-1/2 次幂;采用随机多项式展开方法,若第i个水听器位置处拷贝场随机复声压为Pi,第j个水听器位置处拷贝场随机复声压为Pj,利用式(4)中随机多项式的正交性,两处复声压的互谱即拷贝场互谱矩阵第i行第j列元素数值为随机多项式展开法对复声压互谱矩阵的估计误差随展开截断幂次N的增加指数衰减。若式(5)声学抛物方程的计算在深度上的网格点数为Z,蒙特卡洛统计方法和随机多项式展开方法的时间复杂度分别为O(Z×M)和O(Z3+Q3)。在浅海、低频和一定声传播距离内,随机多项式展开方法较蒙特卡洛统计方法存在一个数量级的效率优势[24]。
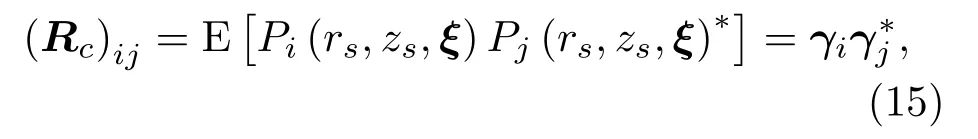
2 数值模拟及结果
为了验证多特征向量约束的匹配场声源定位算法中,随机多项式展开方法对蒙特卡洛统计方法在计算拷贝场互谱矩阵上的效率优势以及算法性能,采用南中国海北部声传播起伏实验SWSF2015[39-40]中的观测水文数据作为仿真起伏环境。实验期间内潮波、线性随机内波和孤立子内波导致了声传播路径上海水声速的剧烈起伏[39-40],海水平均声速剖面和声速均方差剖面见图1、图2。声源距离海底2 m,距离海表约107 m,坐底发射10 s脉宽、中心频率200 Hz、带宽50 Hz的线性调频脉冲,收发水平距离为14.73 km。信号由距离海表23~77 m 近似等间隔垂直阵列的16 个水听器接收。匹配场声源定位中,深度上的搜索范围为0~109 m,水平距离上的搜索范围为0~30 km,深度、距离上网格跨度分别为2 m、10 m。
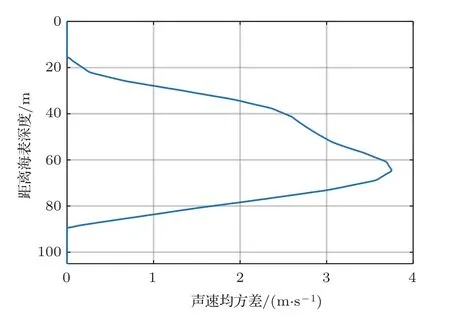
图2 统计均方差声速剖面Fig.2 The depth-dependent standard deviations of the sound speeds
如式(1)~(2),本文采用深度上的第一阶经验正交函数表示海水声速起伏在深度方向上的分布,并使用Karhunen Loève 展开[25]近似不同水平位置处随机系数。其中,随机变量ξ的维度L=10,以保证各深度位置处模拟近似声速的均方差近似等于实际声速均方差。以式(5)中嵌入随机多项式展开的声学抛物方程计算声源位于不同搜索网格点时接收拷贝场复声压的随机多项式展开。取展开截断幂次N= 2,此时展开项数目Q= 66。以样本数目M充分大时的蒙特卡洛统计方法估计的复声压互谱矩阵为参考,验证上述展开参数设置下,式(15)中随机多项式展开方法对互谱矩阵估计的准确性。图3为声源深度=107 m,声传播水平距离= 15 km 时,靠近海面最近的23 m 第一个水听器深度的复声压与0~109 m 深度复声压的互谱函数E[P(z0=23 m)P*(z)] 0 m ≤z≤109 m(E代表数学期望):实线代表随机多项式展开方法的计算结果,圆点代表接收垂直阵阵元深度上蒙特卡洛统计结果。可知,随机多项式展开法可较为准确地估计复声压在深度方向上的互谱函数。
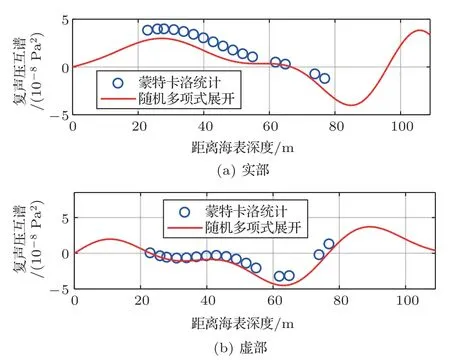
图3 深度方向上复声压的互谱函数Fig.3 The correlation function of the complex pressures
基于式(1)~(2),多次抽样海水声速并计算对应的垂直阵列接收的复声压信号,以此为模拟的测量场,分别采用线性匹配器(Bartlett)[41],对角加载的最小方差无失真匹配器(MV)[42-43](约束白噪声增益小于6 dB)和基于蒙特卡洛统计(MV-EPC-MC)和随机多项式展开(MV-EPC-PC)的多特征向量约束最小方差匹配器模拟定位声源位置。比较4 种匹配场声源定位算法在不同输入信噪比下的定位准确率和输出模糊度的峰均比,同时比较基于蒙特卡洛统计方法和随机多项式展开方法的多特征向量约束最小方差匹配器的计算耗时。
线性匹配器和最小方差无失真匹配器输出模糊度平面分别为式(16)和式(17),
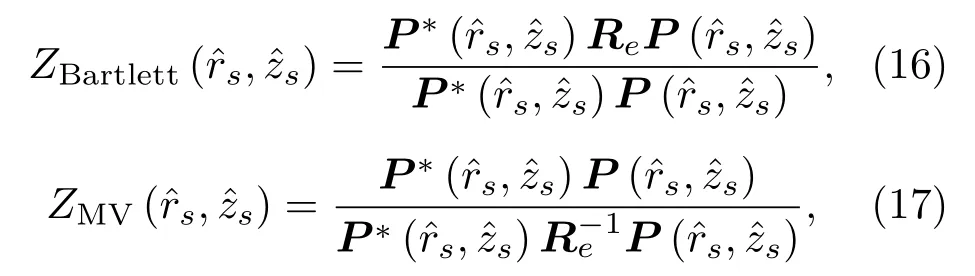
定位准确率中判定为定位正确的“窗口”定义为与真实声源位置误差在深度方向上为±5 m,水平方向上为±500 m,在本算例中为深度落在102~109 m 且水平距离落在14.23~15.23 km。匹配器输出的峰均比(Peak to background ratio,PBR)[44]定义为
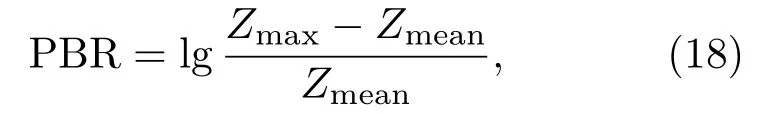
其中,Zmax和Zmean代表各类算法输出模糊度的峰值和均值。
四种匹配器在单水听器的输入信噪比为-10~60 dB 时,定位准确率和峰均比的结果如图4、图5 所示。图6 显示了在定位性能上,由于海水声速的起伏,线性匹配器与白噪声增益约束的对角加载最小方差无失真匹配器在定位准确率上最高只能达到29%,与之相比,高信噪比下基于蒙特卡洛统计的多特征向量约束最小方差匹配场处理器在定位准确率和输出峰均比上明显优于线性匹配器和最小方差无失真匹配器。在输入信噪比在25 dB 以上时,定位准确率在84%,输出峰均比在42 dB。基于随机多项式展开方法的多特征向量约束最小方差匹配场处理器在性能上略逊于前者,定位准确率和输出峰均比达到78% 和38 dB。式(2)中近似海水声速起伏的Karhunen Loève 展开截断和式(3)中近似随机复声压的随机多项式展开幂次截断引起的拷贝场复声压互谱矩阵的估计误差是导致定位算法性能下降的原因;在计算时间上,如表2 所示,使用多特征向量约束的匹配场算法中,在估计拷贝场互谱矩阵时,随机多项式展开方法的时间开销不到蒙特卡洛统计方法的7%。
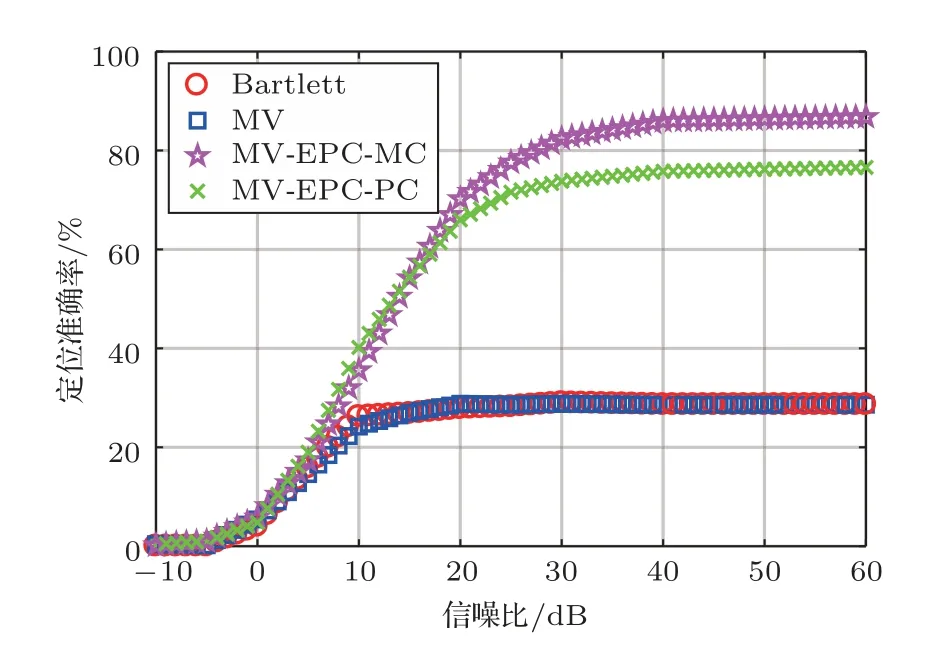
图4 不同信噪比下Bartlett、MV、MV-EPC-MC 以及MV-EPC-PC 四种匹配器的声源定位准确率Fig.4 Probability of correct localization vs SNR per snapshot as a function of four matched filed processors: Bartlett,MV,MV-EPC-MC,and MV-EPC-PC
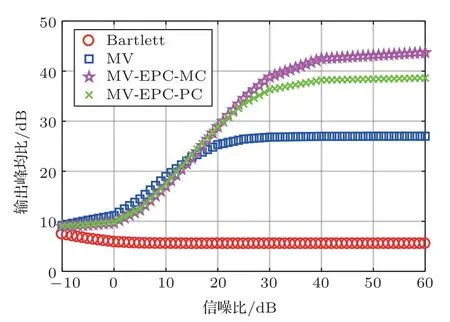
图5 不同信噪比下Bartlett、MV、MV-EPC-MC 以及MV-EPC-PC 四种匹配器输出模糊度的峰均比Fig.5 PBRs vs SNR per snapshot as a function of four matched filed processors: Bartlett,MV,MVEPC-MC,and MV-EPC-PC
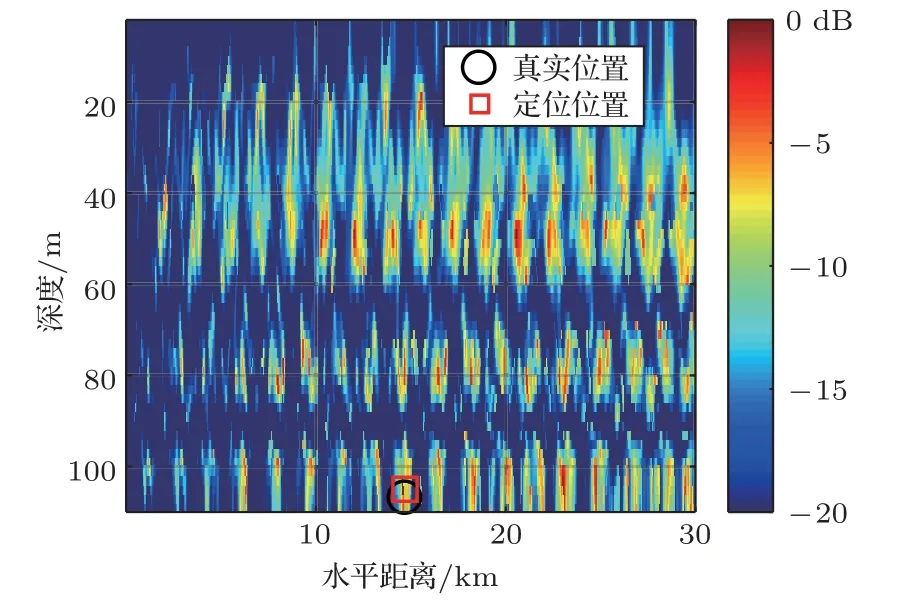
图6 基于随机多项式展开的多特征向量约束最小方差匹配器(MV-EPC-PC)的输出模糊度Fig.6 MV-EPC-PC normalized ambiguity surface

表2 多特征向量约束匹配场声源定位算法的时间开销Table 2 The time cost of the MV-EPC source localization algorithms
3 结论
本文提出了一种基于复声压随机多项式展开的多特征向量约束不确定场声源定位方法。通过将随机声压表示成随机多项式展开的形式,提高了估计拷贝场复声压互谱矩阵的计算效率。在浅海、低频、海水声速存在起伏时,多特征向量约束的匹配场声源定位算法在定位性能(定位准确率和输出峰均比)上优于线性匹配器和最小方差无失真匹配器,算法在估计拷贝场复声压互谱矩阵时,与蒙特卡洛统计方法相比,使用随机多项式展开方法会使得算法在定位性能略逊于前者,但计算效率比之提升一个数量级。
