基于压痕载荷的幂硬化金属材料力学性能确定方法
2022-09-16路景智贾宇磊
薛 河,路景智,贾宇磊,王 帅
(西安科技大学 机械工程学院,西安 710054)
0 引言
工程结构中的许多部件都是通过焊接技术连接的,如核电压力容器及管道等。焊接工艺的特点使得焊接接头成为重要机械结构破坏的薄弱区域[1],并且在经过焊接、弯曲、打磨等加工后,焊接接头区域的材料力学性能会呈现出不均匀的特点[2]。通过传统的拉伸试验获取材料力学性能时,需要在待测部位进行破坏性取样,因此难以对处于不均匀力学状态的焊接接头材料力学性能进行准确地分析[3-5]。微纳米压痕试验作为一种无需取样的技术,因其操作简单、执行速度快、破坏性小等优势,已逐步成为测试在役设备材料力学性能的重要方法[6]。
微纳米压痕试验起源于材料的硬度试验[7]。随后,有学者提出使用压痕试验技术来表征材料的硬度和弹性模量[8-9]。HAGGAG等[10-12]开发了一种原位测试系统,利用自动化球压痕技术(ABI)确定材料的力学性能参数。LEE等[13]探究了不同应力状态下压痕载荷-压入深度曲线的变化情况,建立了通过两个主应力分量之比计算表面应力的理论模型。LEE等[14]通过基于增量塑性理论的有限元分析,研究了主要材料性能参数对压痕载荷-压入深度曲线的影响。近年来,国内学者也对压痕试验的发展进行了相应的研究。姚博等[15-17]基于能量原理,提出了利用压痕载荷-压入深度曲线获取材料应力应变关系的半解析预测模型,并验证了其准确性和有效性。ZHANG等[18]提出了一个考虑到球形压痕试验中塑性变形的修正弹性模量计算模型,提高了弹性模量的计算精度。伍声宝等[19]利用球压痕法测量了材料的拉伸性能,并探究了压头刚度对压痕试验测试结果的影响规律。苏成功等[20-23]通过与单轴拉伸试验进行对比,验证了连续球形压痕试验方法在测量在役设备金属材料力学性能时的有效性与准确性。还有学者对球形压痕下的表征应力应变进行了优化,但容易受到压入过程中材料凸起/凹陷的影响,增加了测试压痕响应参数时的不确定性[24-25]。此外,张志杰等[26]基于能量等效假定提出了将压痕载荷-压入深度曲线与Hollomon律相关联的材料参数半解析模型。XUE等[27]采用连续球形压痕试验结合有限元反演分析,提出了一种获取不锈钢材料应力-应变关系的计算方法。
目前,利用球形压痕试验获取材料力学性能的研究主要集中在通过无量纲方程计算材料力学性能参数,但计算过程较为繁琐且精度无法保证。为了建立更为简便的材料力学特性计算方法,本文利用Abaqus建立三维有限元模型模拟单次球形压痕试验,探究不同材料力学参数下压痕载荷的变化规律;引入对数化压痕载荷的概念,对125种不同参数组合的材料进行有限元模拟,建立基于压痕载荷的材料力学参数计算方法,最大化降低处理压痕响应参数时出现的不确定性。
1 球形压痕试验原理
球形压痕试验是在被测试样表面同一压入点处进行的加卸载过程,即控制压头沿垂直于试样表面的方向以一定的速率进行加卸载,每次加卸载构成一个循环。在压入过程中,只允许压头沿竖直方向进行移动,通过载荷与位移传感器实时监测压入过程中不同压入深度下的载荷。图1示出典型球形压痕试验的压痕载荷-压入深度曲线。借助于有限元反演分析,可以将压痕响应参量转化为材料的力学性能参数。
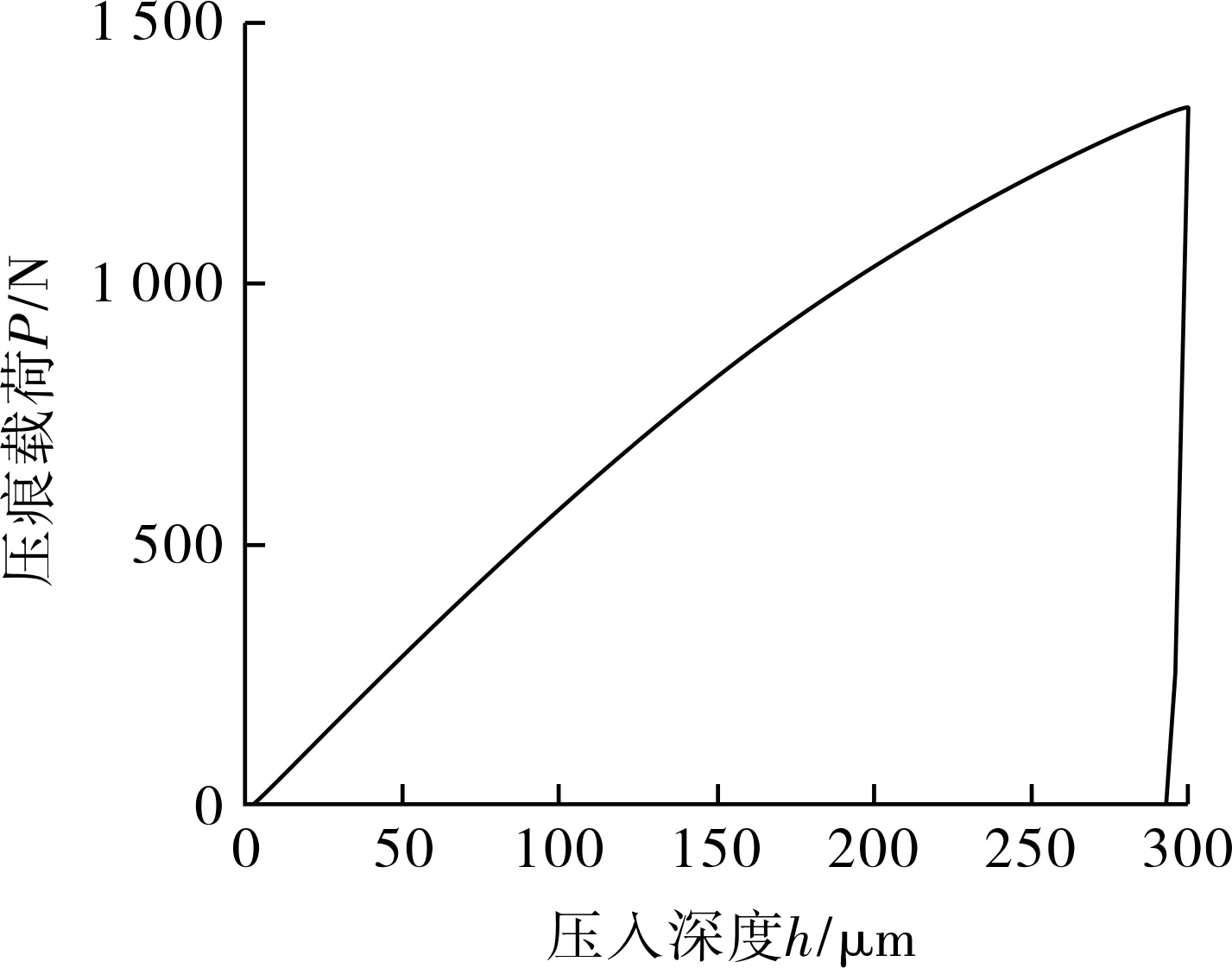
图1 典型球形压痕试验压痕载荷-压入深度曲线
对于大多数常见金属材料而言,其弹塑性行为可以用Hollomon方程近似描述为:
(1)
式中,E为弹性模量;ε为总应变;K为强化系数;n为应变硬化指数;ReL为屈服强度。
当σ>ReL时,式(1)可以改写为:
(2)
式中,εp为总应变中超过屈服阶段的非线性部分应变。
2 有限元模拟
采用Abaqus软件建立三维有限元模型模拟球形压痕试验过程,考虑到试样结构及所受载荷具有对称性,故建立1/4圆柱体模型。参考GB/T 22458—2008《仪器化纳米压入试验方法通则》,为避免试验结果受试样支座的影响,试样厚度应大于或等于压入深度的10倍或压痕半径的6倍,因此将模型中试样尺寸设为10 mm×10 mm×3 mm。球形压头直径为1 mm,由于球形压头材料为碳化钨,其弹性模量远大于被测材料,在压入过程中不会发生变形,因此将其设置为刚体。
边界条件设置为试样底面完全固定,在对称面上施加对称性约束。对压头参考点施加位移载荷,使其只能沿垂直于试样表面的方向移动,最大压入深度h=0.3 mm,加载过程为准静态过程。在压头与被测试样表面之间设置面面接触,库伦摩擦系数设为0.15,有研究[28]表明,该值能够反映压头与试样的实际接触情况。材料选择Hollomon幂硬化本构模型,遵循von Mises屈服准则。
在压入过程中,试样的变形主要发生在与压头的接触区域,而在远离压头的区域却几乎不受影响。为了兼顾计算精度与计算效率,对靠近压头部位的网格进行细化(如图2所示),可以保证压痕测试局部区域的响应精度。对于压头的非接触区域,网格单元尺寸也逐渐增大。网格单元类型设置为C3D8R,可以保证在复杂应力状态下的计算精度。

图2 有限元模型及网格划分
在有限元模拟过程中,网格单元尺寸会对模拟计算结果产生较大影响,网格尺寸过小会降低运算速率;网格尺寸过大则会降低运算精度。为确保计算结果不受网格尺寸的影响,设置了不同尺寸的网格进行无关性验证,参数如表1所示。

表1 网格无关性验证中采用的最小网格尺寸
在不同网格尺寸下,模拟结果都可快速收敛且具有较好的一致性(如图3所示),但运算速率会随着网格尺寸的缩小而显著降低。综合考虑后,在后续的计算中将试样的最小网格尺寸设为 0.025 mm。

图3 网格无关性验证的结果
3 有限元结果分析与讨论
材料的力学性能决定了其抵抗变形的能力,当材料具备不同的力学性能时,达到相同的变形程度所需要承受的载荷也不同。为研究材料不同力学性能时的压痕载荷的变化规律,对式(1)中的材料力学性能参数设置了单一变量模拟组,具体材料参数设置如表2所示。

表2 单一变量模拟组材料参数
3.1 弹性模量对压痕载荷的影响
在模拟组1中,控制屈服强度与应变硬化指数不变,以弹性模量为变量进行了模拟球形压痕试验,图4示出在不同压入深度下各弹性模量所对应的压痕载荷曲线。可以看出,在屈服强度与应变硬化指数相同的情况下,随着弹性模量的增加,使材料发生一定弹性变形所需的应力也越大,即在压入相同深度时所需的载荷也就越大,且在不同的压入深度下具有相同的变化趋势。在进行对数化处理后发现,lnE与lnP之间表现出良好的线性关系(如图5所示),可用以下函数关系表示二者之间的关系:
lnP=alnE+a0
(3)
式中,a,a0为系数。

图4 不同弹性模量E对应的压痕载荷P关系曲线

图5 压痕载荷与弹性模量对数关系曲线
3.2 屈服强度对压痕载荷的影响
在模拟组2中,控制弹性模量和应变硬化指数不变,以屈服强度为变量进行了模拟球形压痕试验,图6示出不同压入深度下屈服强度与压痕载荷的关系曲线。 可以看出,屈服强度的增加使得材料不易发生变形,因此在发生相同的变形程度时所需的载荷也随之增加,且当压入深度增大时,载荷增量的变化也更为明显。经对数化处理后发现,lnReL与lnP之间具有明显的线性关系(见图7),因此可用以下函数关系表示二者之间的关系:
lnP=blnReL+b0
(4)
式中,b,b0为系数。

图6 不同屈服强度ReL对应的压痕载荷P关系曲线

图7 压痕载荷与屈服强度对数关系曲线
3.3 应变硬化指数对压痕载荷的影响
在模拟组3中,控制弹性模量和屈服强度不变,以应变硬化指数为变量进行分析,图8示出不同压入深度下应变硬化指数所对应的压痕载荷曲线。
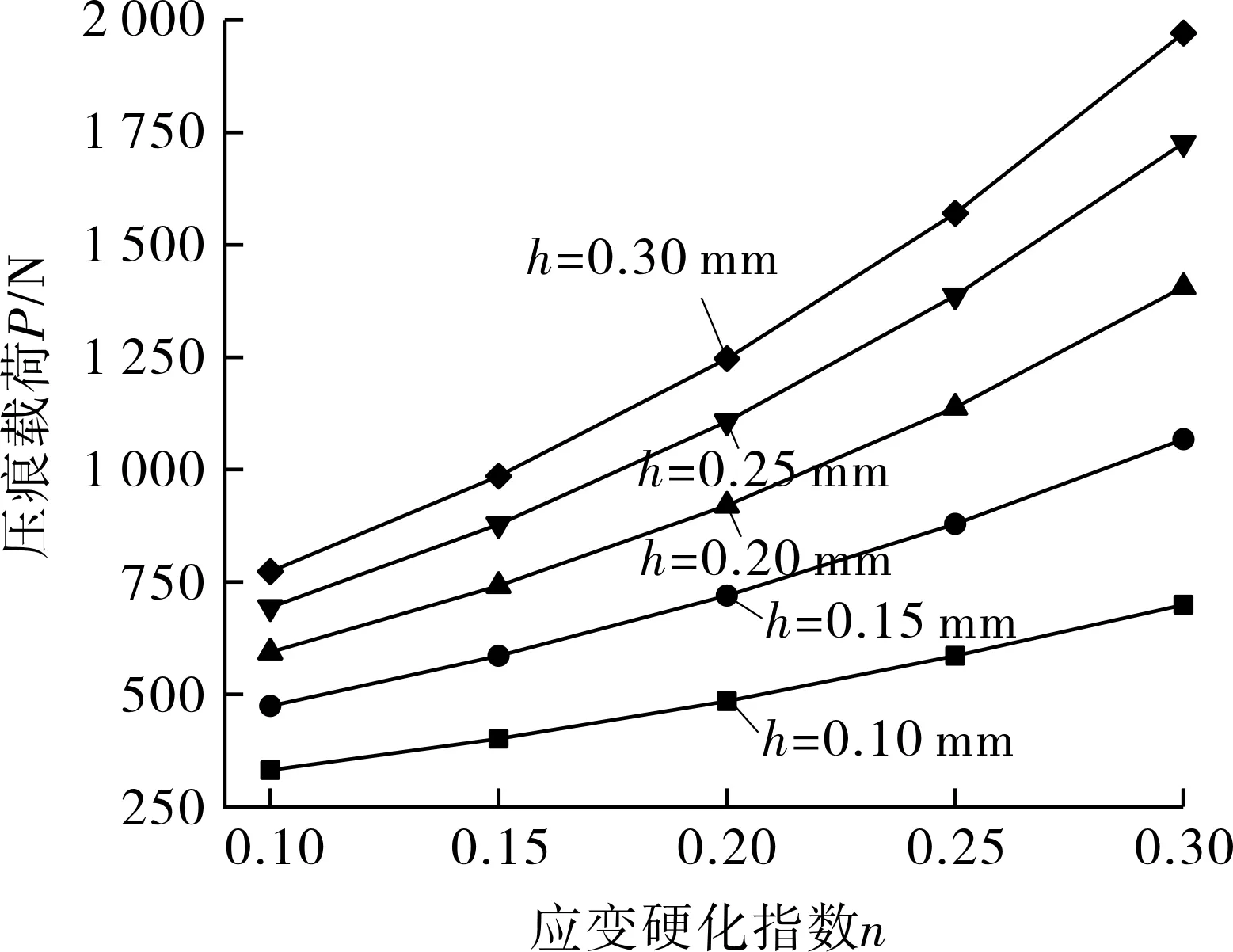
图8 不同应变硬化指数n对应的压痕载荷P关系曲线
从图8可以看出,应变硬化指数的增加使得材料的硬化程度增强,抵抗塑性变形的能力也随之增强,且当应变硬化指数增加时,压痕载荷表现出明显的抛物线增长趋势。将压痕载荷对数化处理后发现,lnP相对于n表现为线性增加趋势(见图9),因此二者之间的关系可以表示为:
lnP=cn+c0
(5)
式中,c,c0为系数。

图9 对数压痕载荷lnP与应变硬化指数n关系曲线
3.4 基于压痕载荷的材料力学参数计算方法
通过研究弹性模量、屈服强度、应变硬化指数对压痕载荷的影响发现,压痕载荷与材料力学性能之间存在确定的变化规律,结合式(3)~(5),压痕载荷与材料力学性能参数的关系可用下式表示:
lnP=alnE+blnReL+cn+d
(6)
式中,d为系数。
为进一步确定式(6)中系数的具体数值,在弹性模量E为90~210 GPa,屈服强度ReL为180~300 MPa,应变硬化指数n为0.1~0.3范围内,共得到125种不同参数组合的材料,对每一种材料进行模拟球形压痕试验,得到不同压入深度h下的压痕载荷结果。采用函数关系式(6)对所得压痕载荷数据进行拟合,得到各系数数值如表3所示。

表3 不同压入深度下拟合函数的系数值
4 试验验证
为验证表3中系数数值的准确性,本文以某公司提供的L450管线钢为研究对象。按照GB/T 4340.1—1999《金属维氏硬度试验 第1部分:试验方法》,将未经拉伸的材料薄板轧制成厚度4 mm的薄板,随后利用线切割机进行切割并去除毛刺,最终将L450管线钢薄板加工成板状拉伸试样。板状拉伸试样的几何尺寸如图10所示,L450管线钢主要化学成分见表4。

图10 板状拉伸试样结构尺寸示意

表4 L450管线钢主要化学成分
利用MTS-LPS.105试验机对标距段为100 mm 的板状拉伸试样进行单轴拉伸试验。为保证试验结果的可靠性,进行了3次重复试验,同时在试样标距段粘贴应变片以获取更为准确的应力-应变曲线。取3次试验结果的平均值作为L450管线钢的力学性能参数,测得其弹性模量为198.14 GPa,屈服强度为396.93 MPa,应变硬化指数为0.110 7。
在改造的UTM6103电子万能试验机上进行球形压痕试验,图11球形压痕试验平台。在外接计算机上设置试验参数,压入过程采用位移控制,加载速率0.1 mm/min,最大压入深度h=0.3 mm,整个加载过程为准静态。
为尽可能保证压痕试验结果的稳定性,只针对其中一个拉伸试样进行球形压痕试验。同时,为避免试样表面粗糙度对试验结果造成影响,在进行试验前,分别利用400#,600#,1000#,2000#的水砂纸对试样非标距段部位进行打磨处理,随后使用YMPZ-1磨抛机进行磨抛处理,使其上下表面光滑平整。为了排除试验过程造成的随机误差,在试样测试表面进行3次等间距的球形压痕试验,以获得更为准确的测试结果。

图11 球形压痕试验平台
图12示出L450管线钢3次球形压痕试验的压痕载荷-压入深度曲线,从图中曲线提取不同压入深度下所对应的压痕载荷,利用式(6)计算L450管线钢的力学性能。计算结果列于表5,并与单轴拉伸试验结果的平均值进行对比,可以看出,由3次球形压痕试验获得的L450管线钢材料力学参数的平均值与单轴拉伸结果较为一致,其相对误差均保持在3%以内,可以满足工程要求。
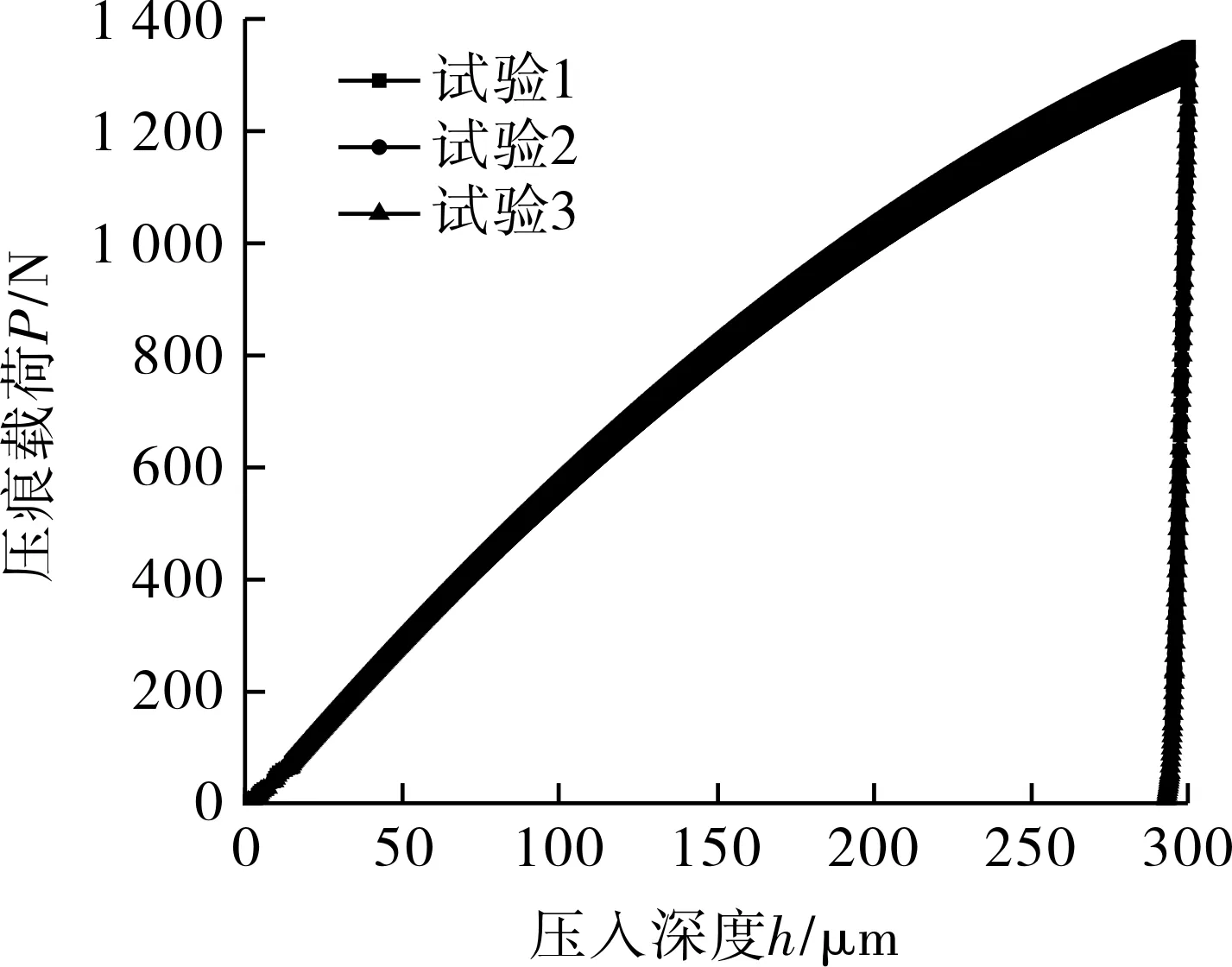
图12 L450管线钢球形压痕试验压痕载荷-压入深度曲线

表5 L450管线钢力学性能参数计算结果
5 结论
(1)通过建立三维有限元模型实现了球形压痕试验的有限元模拟,并分别以弹性模量、屈服强度和应变硬化指数为单一变量,探索了不同材料力学参数下压痕载荷的变化规律。
(2)将压痕载荷进行了对数化处理,从分析结果中发现,压痕载荷与弹性模量和屈服强度之间存在对数线性关系,对数压痕载荷与应变硬化指数之间同样满足线性关系;对125种不同参数组合的材料进一步研究,拟合出表征幂硬化金属材料力学参数的函数关系式。
(3)通过有限元模拟结合球形压痕试验对压痕载荷-压入深度曲线进行分析计算,基于幂硬化模型得到L450管线钢的材料力学参数,与单轴拉伸结果相比,其误差均保持在3%以内,证明了该方法的有效性,可以将其作为测试幂硬化金属材料力学性能参数的有效工具。
