基于改进ShuffleNet V2网络的轴承故障诊断方法

赵志宏，李春秀，杨绍普,张然

(1．石家庄铁道大学 信息科学与技术学院，石家庄 050043；2．省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043)

轴承是机械设备中的关键部件，设备性能与轴承工作状态息息相关，而轴承运行状态极易受到恶劣工作环境和工作时间的影响。据统计，旋转机械中的故障大约有30%与轴承有关[1]，因此，轴承故障诊断一直是研究的热点问题。故障诊断方法利用短时傅里叶变换[2-4]、经验模态分解[5]、小波变换[6]等算法提取轴承故障特征，再结合模式识别方法进行故障诊断[7]。如文献[8]利用希尔伯特-黄变换分析轴承振动信号并通过傅里叶变换提取故障特征；文献[9]利用集合经验模态分解处理轴承振动信号，将得到的样本熵作为故障特征并通过支持向量机进行故障分类。

近年来，随着深度学习的快速发展，越来越多学者将深度学习应用于机械设备故障诊断中：基于堆叠式自动编码器[10]、卷积胶囊网络[11]、改进堆叠式循环网络[12]的滚动轴承故障诊断方法均取得了良好的效果；文献[13]利用谱峭度图包含的时频能量特性对滚动轴承振动信号进行编码并将特征图输入卷积神经网络完成故障分类；文献[14]利用格拉姆角差场方法对轴承振动信号进行图像转换后将其输入卷积神经网络，获得较高的诊断准确率；文献[15]将轴承振动信号进行短时傅里叶变换得到时频谱后输入卷积神经网络进行故障诊断，取得了99%以上的故障识别率。

为取得更高的故障识别率，深度神经网络模型朝着越来越复杂的方向发展，但大而复杂的模型难以应用在真实场景或移动设备中，因此小而高效的神经网络模型具有非常高的研究价值。目前，常用的轻量级网络模型有MobileNet[16]，SqueezeNet[17]，Xception[18]和ShuffleNet[19]。在模型大小相同的条件下，ShuffleNet 的准确率优于MobileNet。ShuffleNet V1主要采用分组卷积和深度可分离卷积来降低模型的参数量以及运算量，但是过多的分组卷积会导致内存使用量增加；ShuffleNet V2[20]去掉了分组卷积，设计了Channel Split操作，在提高模型准确率的同时降低了运算量，但模型结构中仍存在参数冗余和空间信息丢失的问题。基于以上考虑，本文提出一种改进的ShuffleNet V2轴承故障诊断方法，通过去掉ShuffleNet V2基本单元中的一层1×1卷积对模型进行简化，并用空洞卷积替换基本单元中的深度卷积，扩大模型特征提取的感受野，从而提高轴承故障特征提取能力。

1 Morlet小波变换

对于任意的L2(R)空间中的函数f(t)，其连续小波变换定义为

fCWT(a，τ)=[f(t),ψa，τ(t)]=

(1)

式中：a为与频率相关的尺度因子；τ为平移因子；ψa，τ(t)为小波基函数。

连续小波变换的关键在于小波基函数的选取，Morlet小波是一种指数衰减的余弦信号，与冲击衰减波形的轴承振动信号匹配性较好[21-24]，文献[25]利用相关系数度量小波函数与轴承冲击成分的相似性，与5种常用小波函数的对比结果表明Morlet小波最适用于轴承振动信号的分析，能更好地提取轴承故障特征。本文在Morlet小波的基础上，选择其复数形式的CMOR小波，以获取更好的自适应性能[26]，对轴承故障振动信号进行时频转换。

2 ShuffleNet V2及其改进

2.1 深度可分离卷积

ShuffleNet V2模型中采用了3×3深度可分离卷积，其计算量比3×3的标准卷积约少88%，而精度只有很小的损失[27]。深度可分离卷积由深度卷积和1×1逐点卷积两部分组成，深度卷积将单个固定大小的卷积核作用到每个输入通道上，1×1卷积将深度卷积输出的特征进行合并，在不改变输出特征图大小的条件下增强网络表达能力。

2.2 空洞卷积

空洞卷积也称膨胀卷积[28]，是在标准卷积核中注入空洞，将小卷积核尺寸变大的同时保持卷积的参数量不变，扩大的幅度称为空洞率。标准卷积是空洞率为1的卷积，空洞率为2的卷积与标准卷积的对比如图1所示：3×3卷积在空洞率为2的样本特征映射与5×5标准卷积类似，在不增加参数量的基础上扩大了感受野，从而获取更大范围内的特征信息。

(a)空洞卷积

2.3 ShuffleNet V2基本单元

ShuffleNet V2主要由2种基本单元堆叠而成[20]，基本单元结构如图2所示：步长为1的基本单元中，输入数据按照通道数一分为二，进入2个分支，右分支通过2层1×1卷积和3×3深度卷积进行特征提取，之后与左分支输入进行通道级联合并两部分数据，再通过通道混洗(Channel Shuffle，CS)均匀地打乱信息的顺序；步长为2的基本单元主要进行降采样操作，相比步长为1的基本单元，其取消了通道分开步骤并在左分支部分增加了1×1卷积和3×3深度卷积，使输出通道的数目增加了一倍，特征图大小减半。在基本单元中，卷积操作之后均采用Batch Normalization(BN)层加快网络收敛速度，在1×1卷积之后还采用了Relu函数增加模型的非线性特征。

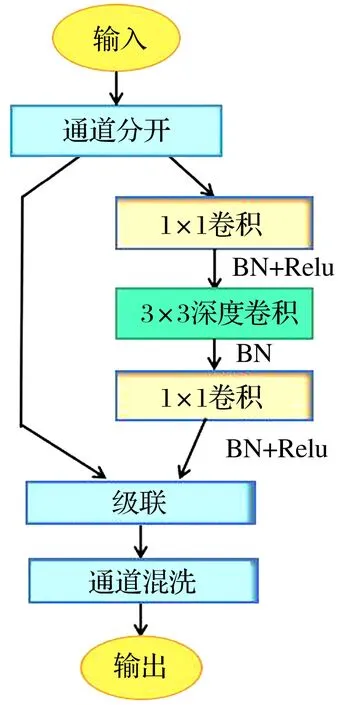
(a)步长为1

2.4 ShuffleNet V2改进单元

改进的ShuffleNet V2基本单元如图3所示，与原模型相比，改进的基本单元去掉了右分支中最后的1×1卷积，并将步长为2单元中的3×3深度卷积替换为空洞率为2的空洞卷积，原因如下：

(a)步长为1

1)深度可分离卷积中，1×1卷积作用是融合通道间的信息，ShuffleNet V2基本单元右分支中有2层1×1卷积，去掉一层1×1卷积仍然可以实现信息融合，但可以减少模型参数量，提升模型泛化能力。

2)采用空洞卷积对基本单元中的深度卷积进行替换，可以在不增加参数量的条件下增大感受野的范围，提高模型的特征提取能力。

3 基于改进ShuffleNet V2的轴承故障诊断模型

基于改进ShuffleNet V2的轴承故障诊断模型的诊断过程如图4所示：首先，将获取的轴承数据按照一定长度进行划分并编号，按一定的比例划分为训练集、验证集和测试集：其次，采用CMOR小波将划分好的数据转换为时频图；然后，将训练集数据输入改进ShuffleNet V2网络进行训练，调整模型相关参数完成训练并采用验证集验证模型；最后，将测试集输入验证过的模型进行故障识别。

图4 改进ShuffleNet V2模型诊断过程

改进ShuffleNet V2网络模型的具体结构见表1，其中阶段2，3，4部分是ShuffleNet V2改进单元的堆叠结构，数目代表单元的堆叠数目，步长代表的是当前ShuffleNet V2改进单元的类型。

表1 改进ShuffleNet V2 网络的结构

4 试验分析

4.1 试验数据

为验证本文模型的性能，选用凯斯西储大学轴承数据集[29]中驱动端的6205-2RS 轴承数据，采样频率为12 kHz，转速为1 797 r/min。试验数据集见表2，将轴承振动信号进行分割，每864个采样点作为一个样本，每种类型的数据构造300个样本，按7:2:1的比例将构造好的样本随机划分为训练集、验证集和测试集并采用 One-hot 编码[30]方式对10种轴承工作状态赋予标签。

表 2 西储大学轴承试验数据集

采用CMOR小波对数据集进行变换得到二维时频图。以故障直径为0.178 mm的内圈、外圈、钢球的故障信号和正常信号为例，生成的CMOR时频图如图5所示，可以看出轴承的内圈、外圈、钢球故障和正常轴承的CMOR时频图明显不同。

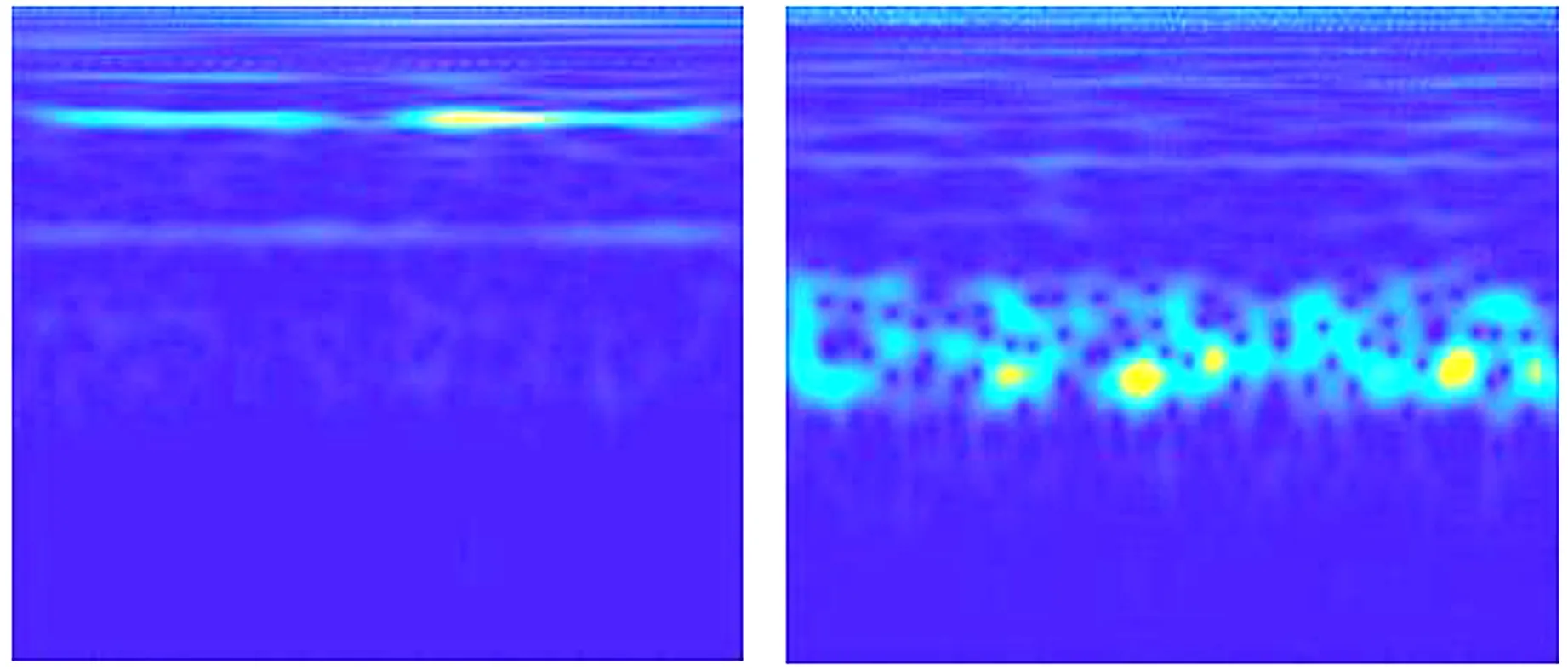
(a)正常状态 (b)钢球故障

4.2 改进模型分析

采用试验数据生成的时频图作为输入，模型使用Adam优化算法，交叉熵损失函数，迭代次数为40，学习率设置为0.001，通过试验确定改进模型中空洞卷积的空洞率以及改进单元的选择。

4.2.1 空洞率的影响

空洞卷积通过设置不同大小的空洞率对普通卷积窗进行空洞填充，不同的空洞率会获得不同的感受野，空洞率过大时会带来局部信息缺失和所获取信息相关性低等问题。去掉ShuffleNet V2基本单元中的一层1×1卷积并将3×3深度卷积替换为空洞卷积，空洞率设置为1，2，3分别进行5次试验，结果见表3，空洞率为2时模型的准确率最高，因此后续试验中采用空洞率为2的卷积进行替换。

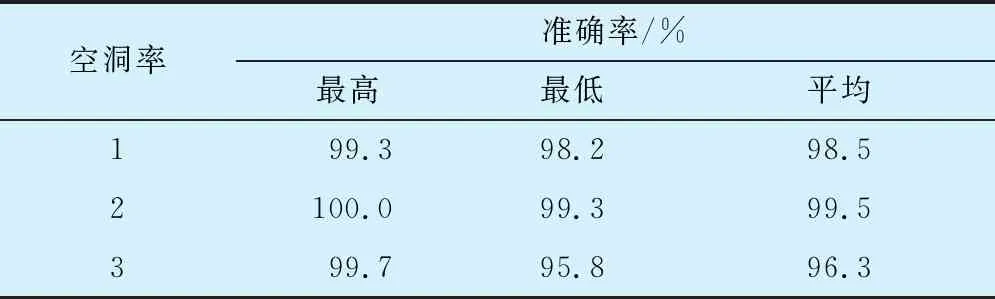
表 3 不同空洞率模型的分类准确率

4.2.2 不同改进单元的影响

ShuffleNet V2网络模型主要是由步长为1和步长为2的基本单元堆叠而成，由于空洞卷积的连续使用会导致局部信息缺失，需研究不同基本单元采用空洞卷积时对试验结果的影响。

模型A代表只对步长为1基本单元中的3×3深度卷积进行空洞卷积替换；模型B代表对所有基本单元中的3×3深度卷积进行空洞卷积替换；模型C代表只对步长为2基本单元中的3×3深度卷积进行空洞卷积替换。分别采用3个模型进行5次试验，结果如图6所示，模型C的准确率更高，因此后续试验模型只对步长为2基本单元中的3×3深度卷积进行空洞卷积替换且空洞率为2。

图6 不同改进单元ShuffleNet V2模型的准确率

4.3 试验结果分析

确定模型的基本单元及空洞率后，分别采用训练集、验证集进行训练和验证，模型的准确率和损失率曲线如图7所示：第5次迭代时模型的准确率已经达到了100%，20次迭代后的准确率也能达到99%以上，此时网络训练至收敛，训练集与验证集的损失函数值也逐渐平稳且趋近于0。将测试集数据输入验证后的模型进行分类，得到的混淆矩阵如图8所示，测试集的故障分类准确率达100%。

图7 改进ShuffleNet V2模型的准确率及损失率曲线

图8 改进ShuffleNet V2模型的分类混淆矩阵

采用T-SNE算法对模型的分类过程进行特征可视化，原始数据及网络层输出可视化结果如图9所示：原始数据集处于混乱状态，很难区分故障类别；经过改进ShuffleNetV2模型第1层卷积后，故障类别由混乱无序状态开始有效的聚集，但类别4，7，9仍存在交叉重叠现象；再经过改进单元卷积层特征提取后，10种故障类别清晰分明，没有出现相互交错现象。

(a)原始数据

4.4 对比试验

在相同数据集条件下，不同轻量级网络模型的对比结果见表4：与简化ShuffleNet V2模型相比，本文模型在参数量一致的情况下有更高的准确率，有效的证明了空洞卷积可以在不增加参数的前提下进一步提升模型的特征提取能力；与MobileNet V2模型相比，本文模型在参数量上节省了约72%，且在多次分类过程中都取得了100%的准确率；说明改进ShuffleNet V2模型在参数量和性能上都优于其他轻量级神经网络模型，更适合部署到移动设备中。

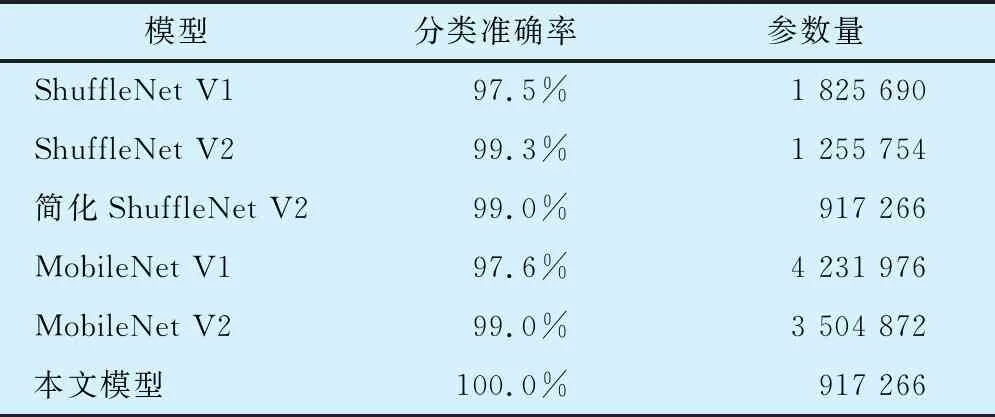
表 4 不同模型的分类准确率及参数量

4.5 模型泛化试验

为验证改进ShuffleNet V2模型的泛化能力，选用12 kHz的采样频率分别采集1 797，1 772和1 750 r/min转速下的轴承数据分为数据集a，b，c，每个数据集均包含10种运行状态，模型泛化能力试验结果如图10所示，其中a→b表示用a数据集训练模型后用b数据集进行测试。由图10可知：在a→c和c→a这2组转速相差较大时，模型的分类准确率较低，泛化能力相对较弱；但由于简化后模型结构相对简单，参数量少，可以减小因参数过拟合带来的泛化误差，本文模型在泛化试验中的平均分类准确率仍可达到97%以上，整体泛化性能较好。

图10 泛化性能对比

4.6 高铁轮对轴承试验

铁路货车轮对轴承试验台如图11所示，由调速驱动电动机、液压与电气控制装置、机架、液压轮对加紧装置、加速度传感器等组成，轴承型号为197726双列圆锥滚子轴承，故障为实际运行过程中自然形成，外圈剥落、滚动体表面损伤和滚动体电蚀如图12所示。采样频率为5 120 Hz，采集水平方向振动信号，4类轴承信号如图13所示，可以看出振动信号呈现非线性、非平稳的特点，故障特征被噪声所淹没。试验过程中，以864个采样点作为一个样本进行二维图像转换，每种类型数据构造300个样本。

图11 轮对轴承试验台

(a)外圈剥落

(a)健康状态

根据前文所述步骤对轮对轴承数据进行试验， ShuffleNet V2模型、简化ShuffleNet V2模型和本文模型分别取得了92.5%，93.3%，96.7%的分类准确率。本文模型的准确率最高，说明其能更好地提取故障特征，具备更好的故障诊断性能。

5 结论

本文提出一种基于改进ShuffleNet V2网络的轴承故障诊断模型并进行了试验研究，从试验中可以得到以下结论：

1)改进的ShuffleNet V2网络不仅在模型参数量和计算量上更有优势，特征提取能力也得到进一步提升，与ShuffleNet V2网络相比，本文模型在更少参数量和计算量的条件下得到了更好的轴承故障识别效果。

2)空洞率对改进ShuffleNet V2模型识别效果的影响非常大，当空洞率为2时取得了最好的轴承故障识别效果，应根据实际工况选择合适的空洞率。

3)泛性化试验结果表明改进ShuffleNet V2模型比其他轻量级网络模型的的泛化性能更好。

4)铁路货车轮对轴承数据集的试验结果表明改进ShuffleNet V2模型的抗噪性更强，更适合实际应用工况。