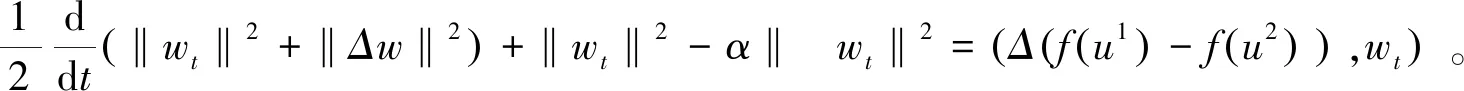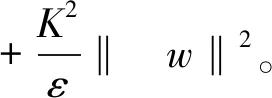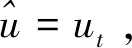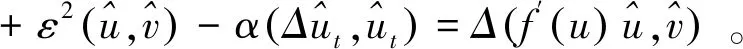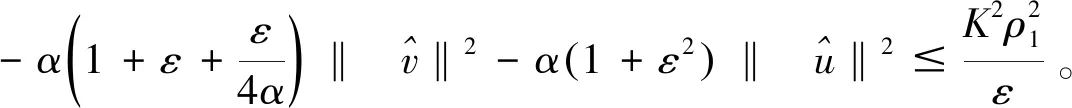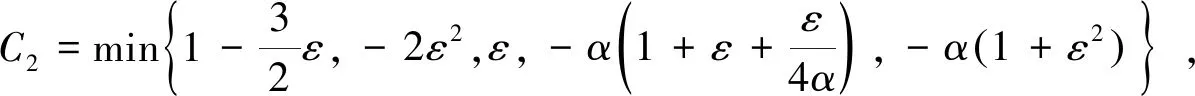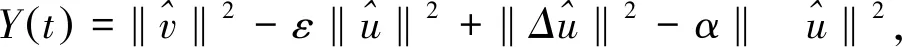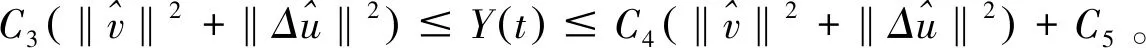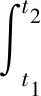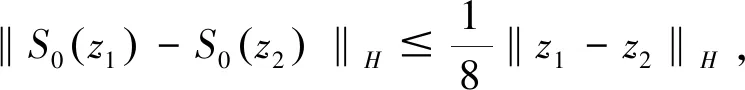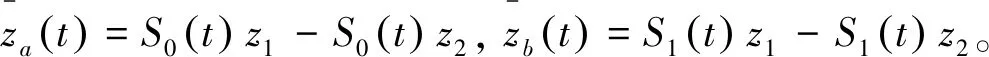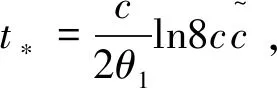具有惯性项的粘性Cahn-Hilliard方程的指数吸引子
2022-09-15张晓雨姜金平王小霞黄厚曾
张晓雨, 姜金平, 王小霞, 黄厚曾
(延安大学 数学与计算机科学学院,陕西 延安 716000)
引言
本文研究的是如下具有惯性项的粘性Cahn-Hilliard方程的指数吸引子问题:

(1)
其中Ω∈R2,g∈L2(Ω),粘性系数α≥0,非线性项f满足如下条件:
f∈C(R,R),|f″(s|≤k0(1+|s|p),∀s∈R,P<1,
(2)
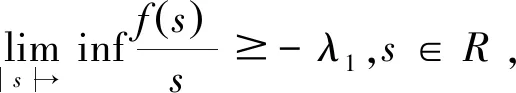
(3)
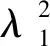
1 预备知识

定义如下Hilbert空间并赋予范数
定义1[5]设{S(t)}t≥0为完备度量空间X中的半群,集合M⊂X称为半群{S(t)}t≥0的指数吸引子,如果满足:
(ⅰ)正不变性:S(t)M⊆M,∀t≥0;
(ⅱ)有限维数:M有有限分形维数,即dimFM<∞;
(ⅲ)集合M⊂X为半群{S(t)}t≥0的指数吸引集,即对每一个有界集B⊂X,存在常数k=k(B),l>0,使得
dist(S(t),B)≤ke-lt。
引理1[6]设χ⊂H是不变紧子集,且W是H的紧嵌入,存在时间t*>0,使得:
(ⅰ)映射(t,z0)→S(t)z0,即[0,t*]×χ→χ是Lipschitz连续的;
(ⅱ)映射S(t*):χ→χ有如下分解形式:
S(t*)=S0+S1,S0:χ→H,S1:χ→W,
其中S0满足
S1满足
‖S1(z1)-S1(z2)‖W≤C*‖z1-z2‖H,
其中C*>0,则半群{S(t)}存在指数吸引子。
引理2[3]假设条件(2)和(3)成立,g∈L2(Ω),u0∈V2,u1∈H,则问题(1)存在唯一解u(t)满足
u(t)∈C([0,T],V2),ut(t)∈C([0,T],H),
并且{u0,u1}→{u(t),ut(t)}在H上连续。
2 有界吸收集
定理1假设非线性项f满足条件(2)和(3),g∈L2(Ω),则问题(1)生成的解半群{S(t)}t≥0在H中存在有界吸收集B=BH(0,ρ1)。
证明选0<ε<1,用v=ut+εu与(1)式做内积,得
+ε‖Δu‖2-α(Δut,ut)-(Δf(u),v)=(g,v)。
(4)
结合Hölder不等式,Young不等式,得
ε2(u,v)-α(Δut,ut)=ε2(u,v)-α‖∇v‖2-αε2‖∇u‖2+2εα(∇v,∇u)
≥-ε2‖u‖‖v‖-2αε‖∇u‖‖∇v‖-α‖∇v‖2-αε2‖∇u‖2
根据条件(2)和(3),利用Sobolev嵌入定理可知,存在K>0,使得
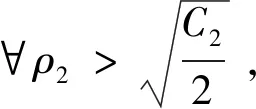
‖f(u)‖L∞ 所以 (5) 且 所以(4)式可记为 令 E(t)=‖v‖2+‖Δu‖2-ε‖u‖2-α‖∇u‖2-(g,u), 则 则有 则 使用Gronwall引理,有 ‖v‖2+‖Δu‖2+‖u‖2+‖∇u‖2≤(‖u1+εu0‖2+‖Δu0‖2+‖u0‖2+‖∇u0‖2)e-2t 其中 ‖v‖2+‖Δu‖2+‖u‖2+‖∇u‖2≤ρ2, 所以若u是(1)式的解,令B=∪t≥0S(t)B′,其中 B′={(u0,u1)∈H:‖u1+εu0‖2+‖Δu0‖2+‖u0‖2+‖∇u0‖2≤ρ2}。 则B为(1)式的解半群在H中的有界吸收集。 定理2对任意R>0和任意z1=(u10,u11),z2=(u20,u21)∈H,使得‖zi‖H≤R(i=1,2),则存在常数Q>0,有 ‖S(t)z1-S(t)z2‖≤eQt‖z1-z2‖H,∀t∈(0,∞), (6) 其中Q是与ε,α,K有关的常数。 wtt+wt+Δ2w-Δ(αwt)-Δ(f(u1)-f(u2))=0。 (7) 用wt与(7)式做内积,得 (8) 且 (9) 把(9)式代入(8)式,得 进一步放缩,可得 其中Q是与ε,α,K有关的常数。 再利用Gronwall引理,可得(6)式。 定理3存在常数M>0,使得 其中z0=(u0,u1),z(t)=(u(t),ut(t))。 (10) (11) 结合(5)式,Hölder不等式,Young不等式及定理1,得 (12) (13) 把(12)式,(13)式代入(11)式,得 (14) 由定理3的有界性及范数的等价性,可得 (15) 对(14)式使用Gronwall引理并结合(15)式,有 其中C3,C4,C5都为正常数。 通过比较,可得出utt和Δut的有界性,则有 即 定理4对∀T>0,映射(t,u0)→S(t)u0,即[0,T]×χ→χ是Lipschitz连续的。 证明对u0,u1∈χ,t1,t2∈[0,T],有 ‖S(t1)u0-S(t2)u1‖H≤‖S(t1)u0-S(t1)u1‖H+‖S(t1)u1-S(t2)u1‖H。 由定理3可得 因此 ‖S(t1)u0-S(t2)u1‖H≤L[|t1-t2|+‖u0-u1‖H]。 其中L=L(T)≥0。 定理5设χ∈H是不变紧子集,且W到H是紧嵌入,则映射S(t*):χ→χ有如下分解形式: S(t*)=S0+S1,S0:χ→H,S1:χ→W。 并且S0和S1满足下列不等式: (16) (17) (18) 使用Poincaré不等式,有 引入泛函 由范数的等价性,当ε足够小时,有 (19) 其中c是正常数。 记θ1=1-ε,有 结合(19)式,得 利用Gronwall引理和(19)式,有 结合(5)式及定理3的有界性,有 则 (20) 则有 在(0,t*)上积分,结合初值条件,有 其中 因此, 定理6设非线性项f满足条件(2)和(3),g∈L2(Ω),则问题(1)生成的解半群{S(t)}t≥0在χ上存在指数吸引子。 证明可由定理4和定理5得到指数吸引子的存在性。
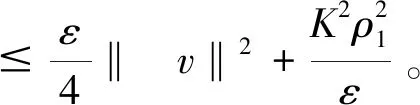
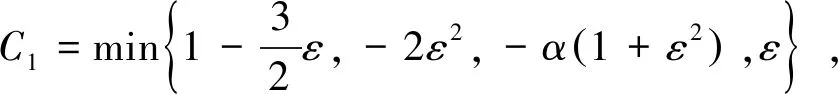
3 指数吸引子