一类比例时滞系统的有限时间稳定性及应用

罗锐，关开中

（五邑大学 数学与计算科学学院，广东 江门 529020）

近几十年来，有限时间稳定性理论和应用引起了人们的广泛关注[1-3]. 一般地说，系统被称为是有限时间稳定的，指的是对于初始条件的给定界，系统的状态在指定的有限时间区间内不超过某个给定的范围[2-3]. 因此，研究系统的有限时间稳定性问题，其本质上是研究系统的解在给定的有限时间区间内的有界性问题. 此外，在某些实际工程领域中，人们不仅希望系统的状态在某一指定的有限时间内不超过给定的范围，而且在达到终点时间之前其状态还能小于所给定的初始值的界限，也就是，系统的解同时具有“有界性”和“压缩性”的特点. 为此，文献[4]提出了有限时间压缩稳定的概念，其后也引起了研究者的关注[3,5].

时滞不可避免地存在于实际系统中，是导致系统性能变差，甚至不稳定的原因之一[6]. 因此，研究时滞系统的有限时间稳定性和有限时间压缩稳定性具有重要的意义. 一般来说，时滞可分为有界时滞和无界时滞两类. 研究表明，有界时滞系统和无界时滞系统在动力学行为方面，存在着显著的差异. 特别是，由于时滞的无界性和可变性，对无界时变时滞系统的动力学的研究则显得更为困难[7]. 值得注意的是，比例时滞作为一类重要的无界变时滞类型常用来描述电动力学、神经网络和非线性动力系统等领域的许多问题[2,8]. 近年来，对比例时滞系统的稳定性等动力学的研究已引起研究者的广泛关注并取得了较为丰富的结果[1-3,9-10]. 然而，已有文献大多是关于比例时滞系统的长时间的稳定性，即Lyapunov意义下的稳定性，而对比例时滞系统有限时间稳定性的研究则不多[2]. Hien等[2]利用M-矩阵理论和分析技巧，研究了一类较为特殊形式的比例时滞神经网络的有限时间稳定性问题，但作者并没有研究此类系统的有限时间压缩稳定性. 最近，文献[3]建立了一类具有常时滞的微分系统有限时间稳定和有限时间压缩稳定的Lyapunov型条件.

基于上述考虑，特别受文献[2-3]的启发，本文将研究比例时滞系统的有限时间稳定和有限时间压缩稳定问题. 我们将发展Lyapunov-Razumikhin方法，来建立较一般形式的比例时滞系统有限时间稳定和压缩稳定的条件，作为该条件的应用，也获得了一类具有比例时滞的神经网络有限时间稳定和有限时间压缩稳定的条件. 最后，通过一个数值例子来说明所获得的理论结果的合理性.

1 模型与预备知识

设R为实数集，R+为非负实数集，Rm表示具有范数的m维实线性赋范空间. 记C （ R+， R+）=｛ψ： R+→R+是连 续的｝ ，K= {a（·）∈ C （ R+， R+）：a（0 ） =0，a（s）关于s是严格递增的}，sgn(y)为关于y的符号函数.

考虑以下一般形式的比例时滞系统

这里q∈（0,1） ,x0= (x1,…,xm)T∈Rm,x（t） = (x1（t） ,…,xm（t）)T∈Rm,f∈C (R+×Rm, Rm)，且对任意的t∈R+，有f（t,0 ）=0.

定义1[11]给定3个正数T,c1,c2，且c1＜c2. 若当x（0） ＜c1时，总有x（t） ＜c2, ∀t∈[0,T]，则称系统（1）关于（c1,c2,T）是有限时间稳定的.

定义2[3]给定5个正数T,c1,c2,η,σ,且η＜c1＜c2,σ∈ （ 0,T）. 若当时，有∀t∈ ［0,T］，且则称系统（1）关于（c1,c2,η,σ,T）是有限时间压缩稳定的.

注1：从定义2可以看出，系统是有限时间压缩稳定的，不仅要求系统状态在指定时间内不超过一定的阈值，同时要求系统在运行至终止时间之前，其状态小于初值的界. 因此，有限时间压缩稳定强于有限时间稳定.

2 主要结果

定理1给定5个正数T,c1,c2,η,σ,且η＜c1＜c2,σ∈ （0,T）. 若存在可积函数Γ（·）：R+→R，函数ω1,ω2∈K，以及连续函数V：［0 ,T］× Rm→R+，使得

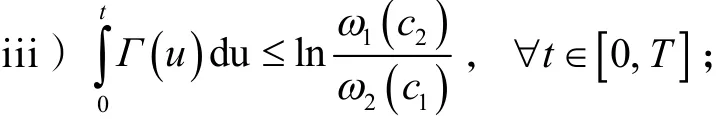
则系统（1）关于（c1,c2,T）是有限时间稳定的.

此外，若还有

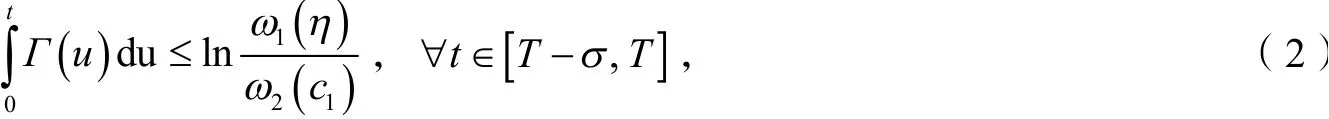
则系统（1）关于（c1,c2,η,σ,T）是有限时间压缩稳定的.

证明设x（t） =x（t,x（0））是系统（1）的解，并记

下面证明

令

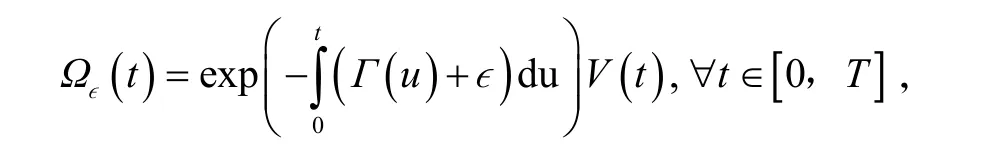
其中∊为任意小的正数.

为证明（3），我们只需证明Ω∊（t） ≤V0, ∀t∈［0,T］. 若结论不成立，并注意到Ω∊（0 ） =V（0） =V0，则存在t*∈（0,T］，使得进一步，由Ω∊（t）的定义可得：

由此可以得到：

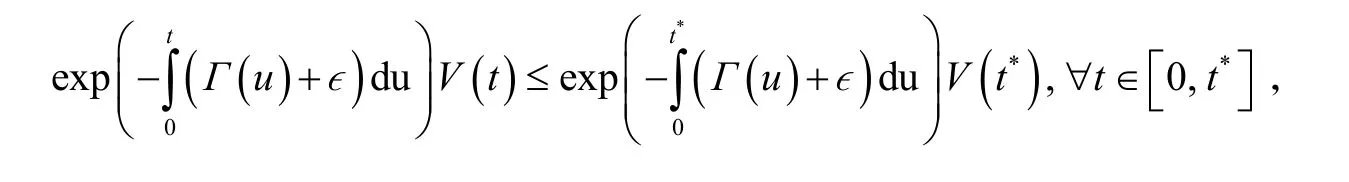
即

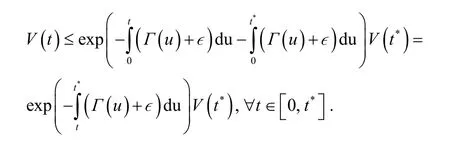
这表明

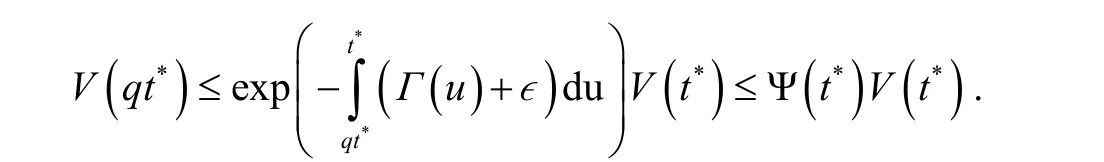
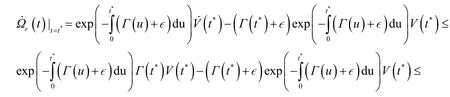
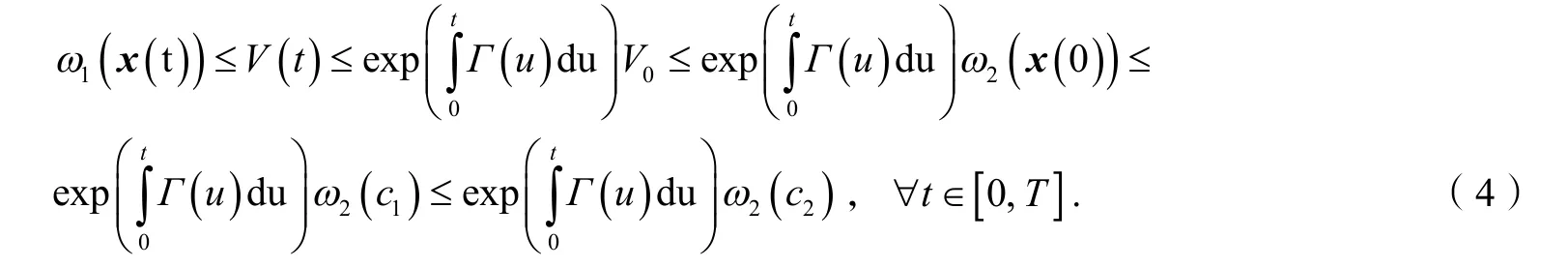
另外，如果式（2）成立，则根据式（4）（除最后一步外），可得

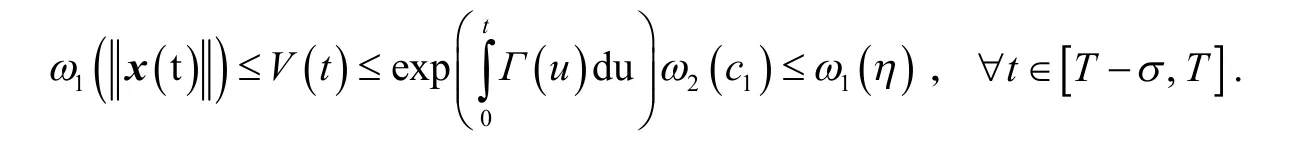
这表明，对于任意的t∈［T-σ,T］，有根据定义2，系统（1）关于（c1,c2,η,σ,T）是有限时间压缩稳定的. 证明完毕.

其次，考虑以下的比例时滞神经网络：

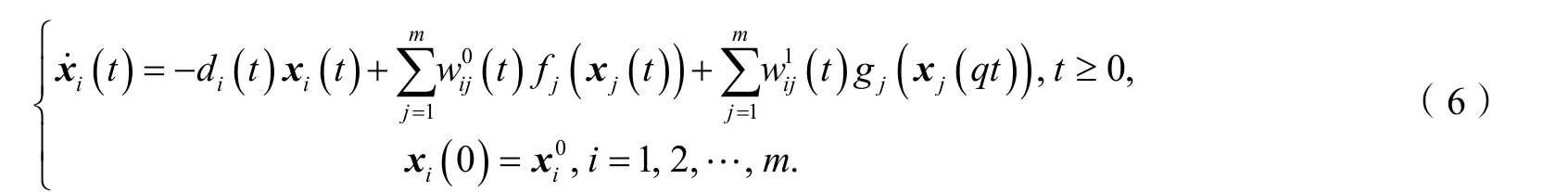
其中n为正数，q∈ （0,1）,xi（t）是关于i的状态向量，和（t）是连接权矩阵，d i（t）是自抑项，是xi（t）在t=0时的初值，f j,gj是激活函数且满足

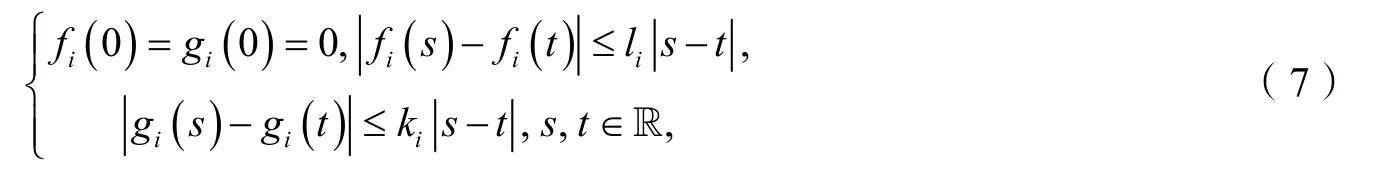
其中li,ki是非负常数，i= 1,2,…,m.

推论1给定5个正数T,c1,c2,η,σ,且η＜c1＜c2,σ∈ （ 0,T）. 如果存在函数Γ（·） ∈C （［0,T］ , R）,使得

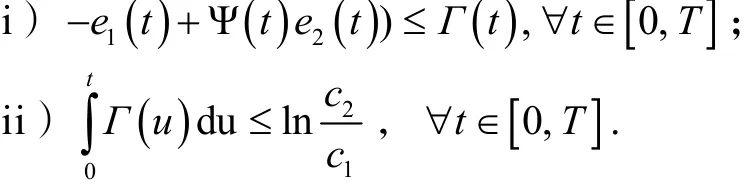
证明设x（t）是系统（6）的解，令根据定理1，Razumikhin条件可写于是

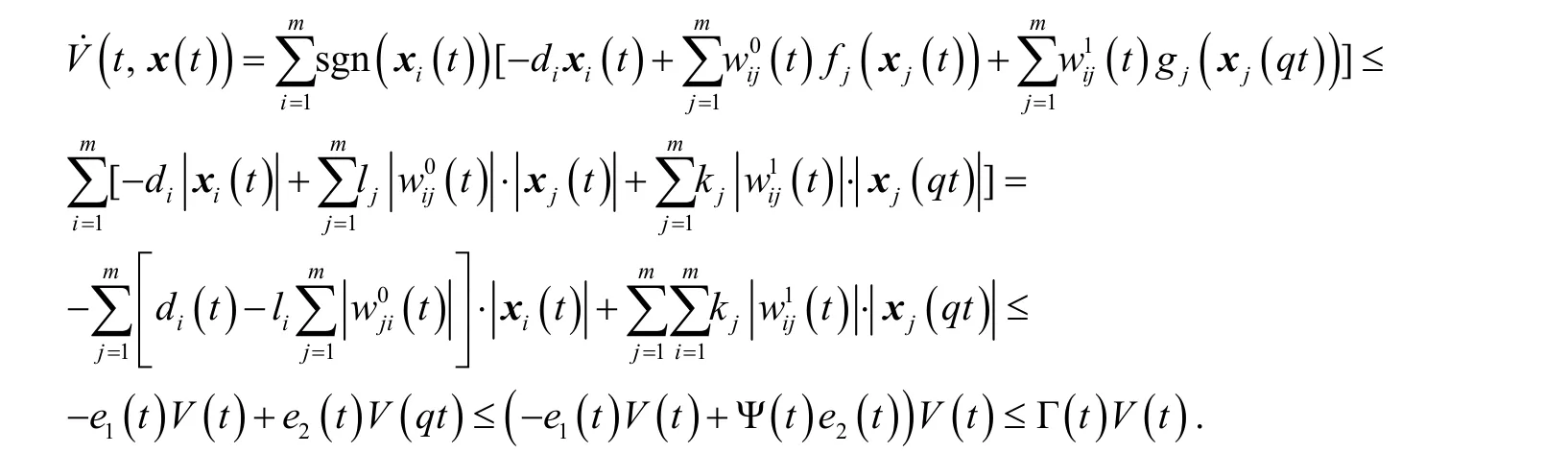
取ω1（s） =ω2（s）=s，则根据定理1，可知推论1成立.

注2：定理1建立了比例时滞微分系统的有限时间稳定性和有限时间压缩稳定性的条件，与文献[3]所讨论的有界时滞不同，本文所讨论的比例时滞是一类无界变时滞. 另外，文献[2]研究了一类具有多比例时滞的神经网络的有限时间稳定性，但并没有考虑有限时间压缩稳定性问题，因此，本文的推论1在一定程度上补充了文献[2]的相应结果.

3 数值算例

在本节中，我们将给出一个数值例子来说明所得结果的有效性和合理性.

例1考虑下面具有比例时滞的非自治二维神经网络：

给 定c1= 0.91,c2= 1.6,η= 0.86,T= 10,σ=1.8以及Γ（t） =0.3cos30.5t+ 0.04. 取li=ki=1，经计算得，e1（t） = 0.59 + 0.05cos （0.5t），e2（t）=cos1.5（0.5t）+0.6，容易验证推论2中的所有条件满足，因此系统（8）关于(0.91,1.6,0.86,1.8,10)是有限时间压缩稳定的. 对于给定的初值x（0） = (0.5， -0.4)T，其数值仿真结果如图1所示.

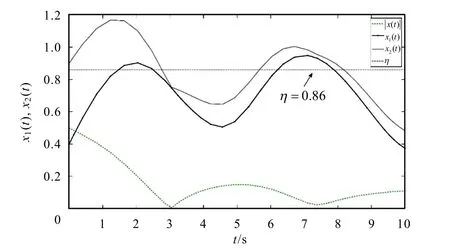
图1 系统（8）具有初值x （0） = (0.5, -0.4)T的状态轨迹