利用迈克耳孙干涉仪测量滤光片特性参数
2022-09-15高崇涵
高崇涵,安 炜,王 峥,徐 平
(北京航空航天大学 中法工程师学院,北京 100191)
滤光片作为重要的光学元件,可以从白光中过滤出一定波长范围的准单色光.滤光片在摄影领域和检测系统中有着广泛的应用,其主要参数为中心波长和带宽.中心波长一般是设备的工作波长,指通带中心位置的波长;带宽指通带中透射率为峰值透射率一半的两个位置之间的波长差.
傅里叶变换光谱仪是一种基于迈克耳孙干涉仪所测量的干涉图样,并经过傅里叶变换来研究和分析光谱的装置[1]. 相对于棱镜光谱仪和光栅光谱仪,它具有扫描速度快、分辨率高、灵敏度高、研究光谱范围宽等优点. 搭建傅里叶变换光谱仪需要综合运用光学、电子学以及数学等多个学科的基础知识,可以训练学生灵活全面地运用多学科知识解决实际问题[2-3]. 本文使用迈克耳孙干涉仪基于傅里叶光学原理对窄带滤光片的特性参数进行测量,并和传统的衍射光栅光谱仪方法进行了对比[4-6].
1 实验原理和实验装置
傅里叶变换光谱仪通过迈克耳孙干涉仪中双光束干涉强度与光程差变化之间的函数关系获得光源的光谱信息,其结构原理如图1所示.

图1 傅里叶变换光谱仪结构原理图
光源发出的光经分光板P1分为两束,两束光分别被定镜M1和动镜M2反射后再度相遇,发生干涉[7]. P2为补偿板,可以抵消定镜M1所反射的光线由于多穿过分光板P1两次所带来的额外的光程差. 为了使动镜匀速移动,将其固定在电机上(型号Ovio-204611). 电机驱动动镜M2匀速缓慢按图1中双向箭头所示方向前后移动,可改变两束光的光程差. 使用基于光敏电阻的光电转换传感器接收干涉光强信号,并将其转换成电信号输出. 输出信号经过放大电路处理后输入到数据采集装置中(型号SYSAM-SP5),进而通过Latis Pro软件进行数据采集和处理.
根据光波叠加原理,若两束单色光在单位长度内的波周数目(波数)都是σ,传播方向、振幅和偏振方向都相同,光强均为I′,两束光之间的光程差为Δ,则这两束光叠加后的光强为
I=4I′cos2(πσΔ)=2I′+2I′cos(2πσΔ)
(1)
上式中的余弦函数分量(以Δ为自变量)的周期就是单色光的波长.对于含有多种波长成分的复色光,干涉总光强中各种波长的光的光强I(σ)与波长有关,那么在光谱间隔σ到σ+dσ内的总光强就是I(σ)dσ.将其代入式(1)并对波数σ做积分即可得整个光谱范围内的总光强为

(2)


(3)

(4)

2 实验测量和数据处理
2.1 商用光栅光谱仪的测量结果
首先用型号为岛津UV-3600的紫外可见近红外分光光度计对待测滤光片的透过率进行了测量.将商用仪器的测量结果作为近似真值与后续实验结果进行对比. 经测量,滤光片的中心波长为580.4 nm,带宽为9.2 nm.
2.2 测量动镜的移动速度
通过数据采集系统只能得到光强随时间的变化曲线,而要想得到光强与光程差之间的变化关系,就需要先测量动镜的移动速度,以便将时间坐标转换为光程差坐标. 动镜被电机驱动,以实现匀速移动,本实验所用的Ovio-204611电机的驱动速度在出厂前已经设定好,仅可调整前进方向,不可调整速度大小.
利用已知波长为532 nm的单色激光来测量动镜的移动速度. 在迈克耳孙干涉仪上调出等倾干涉条纹后,开动电机使动镜匀速移动,干涉条纹的中心就会不断吞入或吐出圆环.注意实验时需将动镜调整到远离光学接触的位置. 将光电转换传感器置于圆环的中心,可以记录该点的光强随时间的变化周期. 实验中采集到的信号是通过光敏电阻的电压,采用光强计对光强与电压关系进行了标定,随后将所测电压数值转换为对应光强,如图2所示.

图2 单色激光干涉光强随时间的变化曲线
2.3 测量滤光片的中心波长和带宽
将激光光源换为白光,并将滤光片置于白光光源与迈克耳孙干涉仪之间(图1中的虚线部分表示滤光片的摆放位置).白光被过滤后成为一束准单色光入射到迈克耳孙干涉仪系统,调节动镜的位置,得到等倾干涉条纹.此时,先向某个方向移动动镜,使干涉条纹消失,再使动镜向相反方向移动,同时使用光电传感器和数据采集系统记录光强随时间的变化曲线,可得到如图3所示的曲线.从图3中可以看到,在10 s到80 s的时间范围内准单色光发生了明显干涉.

图3 白光透过滤光片后干涉光强随时间变化的曲线


图 4 白光透过滤光片后干涉光强中的交流分量随光程差变化的曲线
从图4中可以看出,准单色光的相干长度约为80 μm.利用python的scipy科学计算包,将图4中导出的横坐标和纵坐标的数据进行离散逆傅里叶余弦变换,可以得到不同波长成分所对应的光强与波数σ的关系曲线,即图5所示的光束光谱强度分布I(σ).离散逆傅里叶变换的公式如下:
(5)
(6)
其中sΔ为光程差的采样间隔,sσ为傅里叶余弦逆变换后的离散数据间隔,N为数据点总个数.

图5 光强随波数变化的关系曲线I(σ)

图6 光强随波长变化的关系曲线I(λ)
图6反映了白光经过窄带滤光片后的剩余成分.需要指出的是图6中存在的负光强部分是图5中就已出现的,通过分析式(5)、式(6)可以看出,图5出现负光强是与图4干涉光强随光程差变化曲线的包络线型相关.由于物理上不可能存在负光强,因此,图4干涉光强随光程差变化曲线的包络线在采样时存在一定误差,故通过窗口长度为5的滚动平均算法对曲线进行平滑化去除负光强即可得到如图7所示的最终实验结果.
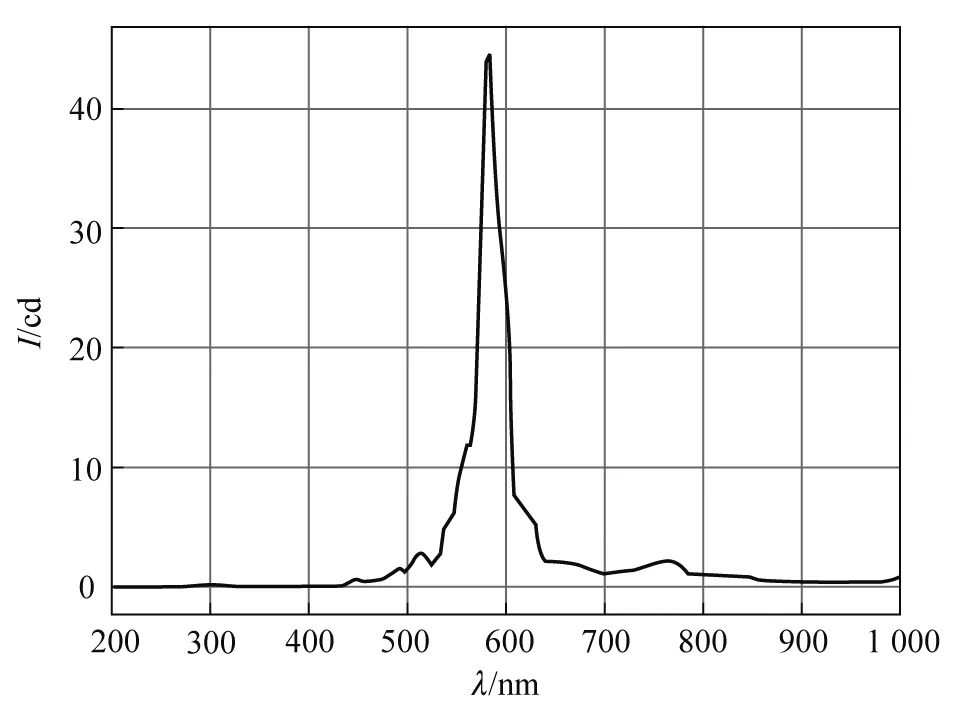
图7 滤光片的透光性能
图7中最高点所对应的横坐标即为滤光片的中心波长.需要注意的是,平滑化会使得带宽提高,带来较大误差.因此需要将图6中透射峰的半高宽作为滤光片的带宽测得值.采用相同的实验方法共测得了10组数据,取平均值作为最终结果:中心波长580.59 nm,带宽10.3 nm. 该结果符合窄带滤光片的特性(带宽小于中心波长的5%),与商用机测得的近似真值相比,中心波长的相对误差约为0.03%,带宽的相对误差约为12%.
2.4 误差分析
相对误差可能来源于实验电机速度,由于实验中采用的电机并不是作严格的匀速运动,而在实验中采用了计算平均速度来估算其理想匀速时的速度,并进行时间与光程差的变换,因此会引入一定误差.另一方面,电机开启到匀速会有一定的暂态响应时间,由于测量单色光相干长度有限,不能采取远离光学接触长时间转动电机以达到稳态的目的,只能在光学接触点附近开启电机,因此,电机的暂态会对数据记录产生一定影响,该影响通过取平均速度带入了计算中.
再者,离散傅里叶变换的处理也会引入一定误差,实验中在80 s的时间内采集了N=80 000个数据点,平均每1 ms采集一次,因此有
t=1×10-3s,
sΔ=2vt=1.12 nm,
sλ=λ2sσ=1.88 nm
傅里叶变换的离散化会带来±0.94 nm的误差.
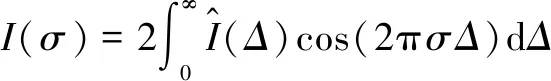

表1 不同采样时间下的实验结果
可以看出,延长采样时间后,结果有向真值收敛的趋势,并且,采样时间在80 s以下时会对实验结果造成影响,而在80 s以上时实验结果趋于稳定. 这是由于采样80 s已采集了有明显波动部分的有效信息.从图4中可以看出快速振荡的载波部分对应了傅里叶变换后的中心波长,而包络线的延展程度则对应了傅里叶变换后的谱线宽度,且包络线越延展,谱线宽度越窄.因此,增加采样时间可以完整记录延展度更高的包络线,从而更加精确地测量带宽.
3 实验结果对比
为了证明傅里叶光谱仪方法的准确性,本文还用衍射光栅法对同样的滤光片进行了测量.

图8 自主搭建的光栅光谱仪结构原理图
实验装置如图8所示,光源发出的平行光入射到平面光栅上,经光栅衍射后,不同颜色的光会分开成独立的谱线,经凸透镜成像在到CCD照相机的感光元件上. 照相机可记录不同谱线的位置,并将记录信息传输给计算机. 根据光栅方程:
d(sinβ-sinα)=kλ
(7)
其中d为光栅常量,β为衍射角,α为入射角,λ为光的波长,k为衍射级数,此处只观察1级条纹.
以汞灯作光源,标定出光波波长与谱线位置的关系,见表2.

表2 谱线位置与波长的关系
对表格中数据进行一元线性回归分析得到波长λ与谱线位置x之间的关系:λ=8.91x+378.46
将光源换为白光,并在光源与光栅之间放置滤光片,使用CCD照相机获取透射光的1级衍射条纹的位置: 22.90 mm,半高宽约为1.30 mm,根据波长λ与位置x之间的关系曲线,得到峰值对应的波长为582.5 nm,滤光片的带宽约11.6 nm. 与商用机测得的近似真值相比,中心波长测量值的相对误差为0.36%,带宽测量值的相对误差为26%.
因此可以得出:在普通物理实验室条件下自主搭建的傅里叶变换光谱仪,相比光栅光谱仪其中心波长相对误差仅为后者的9.2%,带宽相对误差仅为后者的46%,精确度较高. 傅里叶变换光谱仪无需使用已知光源进行标定,使用起来更为灵活.
本实验所使用的光栅长度L=4.5 cm,单位长度的缝数n=300 mm-1. 其分辨本领R可用如下公式计算:
R光栅=kLn
(8)
其中k是所观察的条纹级数,此处为1.计算可得R光栅=1.35×104.而傅里叶光谱仪的R值与动镜行程正相关,理论上分辨本领可随动镜行程增加而达到无穷大[8].因此,可根据实验对于分辨本领的要求增大动镜行程,从而获得较光栅光谱仪更高的分辨本领.
4 结论
本文以实际问题为出发点,融合了光学、数学、电子学等多学科的基础知识,创新性地搭建了傅里叶变换光谱仪,测量了滤光片的特性参数.傅里叶变换光谱仪和光栅光谱仪相比可以更精确地测得滤光片的透光特性.傅里叶变换光谱仪方法基于光学经典实验仪器迈克耳孙干涉仪,结合傅里叶变换等数学知识,可有效提高学生对多学科知识的综合运用能力和实验能力,具有较高的挑战性.
