基于小波优化GRU-ARMA模型的空中交通流量短时预测方法*

闫少华 谢晓璇 张兆宁

（中国民航大学空中交通管理学院 天津 300300）

0 引言

近年来，随着我国空中交通流量不断增加，空域容量趋近饱和，航班延误甚至大面积航班延误时常发生，空中交通管制压力不断增加[1]。为减缓空域压力，降低航班延误发生率，需进一步提高空中交通管理能力，提高空中交通流量短时预测精度。空中交通短时流量预测一般是根据已有的交通数据对未来5，15，30 min或者1 h以上的流量变化情况预测，为管制员提供辅助决策信息，有利于实现动态交通控制与引导。

目前国内外对空中交通短时流量预测的方法主要有：①基于飞行计划的航迹预测；②考虑空中交通流量非线性特征；③机器学习；④基于数据挖掘与智能算法结合组合模型。

在基于飞行计划的航迹预测研究中，陈恺等[2]将计划航迹和实际航迹关联对比分析，结合航向角的平面投影提高了航迹预测的准确度；毛阿芳[3]通过历史数据进行初始航迹预测，建立航空器运动模型，之后随着航空器运动状态的变化不断更新航空器运动模型，修正航迹预测结果，提高了预测精度；Pang等[4]考虑了天气不确定性，提出了基于贝叶斯神经网络的飞机轨迹预测，这种方法能够利用起飞前的最后1份存档飞行计划预测飞机轨迹，包括预测不确定性。在考虑空中交通流量非线性特征的研究中，国内外许多学者通过对时间序列的分析研究中发现了空中交通流具有十分明显的非线性特征，例如混沌性、分形性[5-9]；杨阳[10]利用空中交通流量时间序列具有混沌特性，建立了基于神经网络的流量预测算法。王飞等[11]利用Hurst指数验证了空中交通流量时间序列的分形特性，并且利用相似日的概念对流量进行短期预测，证明了利用分形特征对空中交通流量短期预测是可行的；在利用机器学习对空中交通流量预测中，常用的机器学习有：神经网络模型[12]、K近邻算法[13]、支持向量机模型[14]等。其中，李桂毅等[15]在考虑航段相关性的前提下，利用神经网络建立了交通流参数融合预测模型，预测了航段流量以及密度参数；Pang等[16]将卷积层嵌入长短期记忆模型中，根据对流天气条件以及飞机起飞前的飞行计划预测飞行轨迹；在基于数据挖掘与智能算法结合组合模型研究方面，Guan等[17]通过ADS-B技术建立航空大数据平台，将提取的信息映射到路线上，对不同城市之间的空中交通流量进行计数和预测。尚然然[18]通过分析终端区流量特性，构建基于SOM-k-means算法的相似日聚类模型，最后提出了1种结合聚类分析与LSTM-BP的终端区短期流量预测方法进行未来时段的终端区流量值预测。

以上4种方法在空中交通流量短时预测中都有着广泛的应用，但是都存在一定的局限性，其中，基于飞行计划的航迹预测的计算复杂度会随着流量达到一定程度时迅速增大，而且航班在实际运行中，会受到各种随机因素的干扰，影响航迹预测精度；考虑空中交通流量非线性特征的预测方法，参数设置对预测精度影响较大，主观性较强；单纯依赖机器学习的预测方法只能提取空中交通数据的局部特征；基于数据挖掘与智能算法结合组合模型，具有较强自我学习能力，但是需要大量数据才能挖掘出数据间的复杂关系，数据量少时预测效果不理想。

针对以上问题，本文提出基于小波优化GRU-ARMA预测方法，首先通过对原始流量数据进行多尺度不同频率的小波分解，将原始流量时间序列数据看作不同频率分量的组合，通过小波变换将原始流量时间序列的噪声提取出来，作为噪声项，剩余的数据作为趋势项。其中，趋势项真实反映了原始流量时间序列的随时间演化的总体趋势性，使用门控循环单元（gated recurrent unit，GRU）神经网络模型进行预测，而噪声项则是包含了过去一段时间由于危险天气等突发状况的随机因素的干扰，使用自回归移动平均（autoregressive moving average，ARMA）模型进行噪声项的预测，最后将2个部分结果叠加得到最终的预测结果。

1 预测模型

1.1 小波变换预处理原始流量数据

考虑到空中交通流量会受到危险天气、军方活动等各种时变性较强的随机因素的影响，并且这些因素对于空中交通流量的影响程度不同，可将空中交通流量看成各种频率的分量集合，认为不同频率的分量对空中交通流量的动态影响具有不同的重要性。小波变换（wavelet transform，WT）是1个专门用于时频分析的工具，所以笔者先使用小波变换对原始流量数据进行预处理，将其分解成低频子分量的趋势项和高频子分量的噪声项，再用不同模型分别对这些不同频率的趋势项和噪声项进行预测，降低随机因素对预测精度的影响。

小波变换的本质是抑制时间序列中的无用信息，增大有用信息占比的过程，本文中通过小波变换降低随机因素的干扰，保留真实的流量变化趋势。小波变换的过程如下。

1）选择适当的小波基函数，确定分解层数分解原始信号。小波基函数的种类主要有Haar，dbN，symN，biorN小波等，它们都是小波族，每个小波族里面还包含着具体的小波函数。在对原始流量数据进行小波分解的过程中，不同的分解层数会导致原始流量数据表现出不同程度的趋势性及随机性，影响后续预测精度。

通过选择合适的小波基函数及分解层数，将原始流量时间序列f(t)分解成多个部分的叠加。

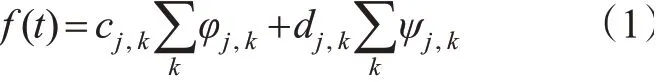
式中：φj，k为近似分量；ψj，k为细节分量；cj，k与dj，k为近似分量和细节分量对应的系数。近似分量代表着原始流量时间序列的低频部分，细节分量代表着原始流量时间序列的高频部分，但低频和高频是1种相对值，并不表示频率的绝对大小。原始流量数据经小波选定的分解层数进行分解之后，每个分解层数都可以得到对应的高频和低频信号。

2）设置合理的阈值，对小波系数进行估算。本文选用启发式阈值确定阈值，综合固定阈值与无偏风险估计阈值的优势。

如果crit＞eta，选择固定阈值作为阈值；如果crit≤eta，则比较固定阈值和无偏风险估计阈值，选择较小的值。

其中，固定阈值为

式中：N为信号的长度；σ为噪声方差，通过鲁棒中值定理[19]计算得出。

无偏风险估计阈值的计算分为3个步骤。

步骤1。把信号s进行绝对值和升序处理，得到新的信号序列。

步骤2。如果设置阈值为f(k)的第k个值的平方根，即

则该阈值产生的风险为

步骤3。根据Risk(k)，取最小风险点相对应的值k(min)，无偏风险估计阈值定义为

3）小波重构。将原始流量时间序列f(t)分解成趋势项trend(t)与噪声项noise(t)之和。

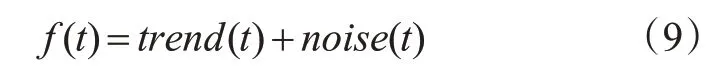
1.2 GRU神经网络模型预测趋势项

GRU神经网络模型是1种适用于时间序列预测的神经网络模型，包括控制上一时刻到当前时刻信息的量的更新门（update gate），以及决定了上一时刻信息在当前时刻的写入程度的重置门（reset gate）。通过引入更新门和重置门决定提取历史流量数据的量以及如何与新的流量数据结合，对趋势项进行预测，其算法原理图见图1。

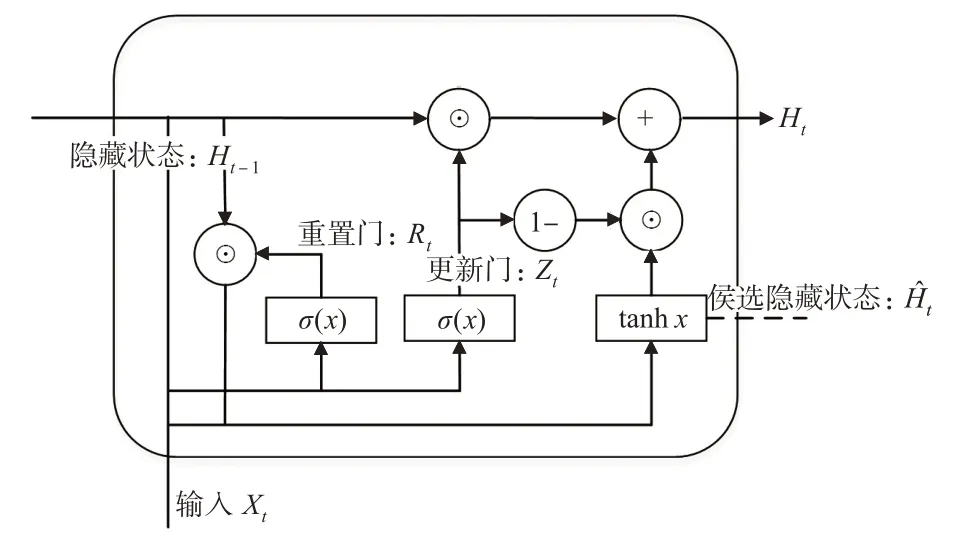
图1 GRU算法原理图Fig.1 The structure of Gated Recurrent Unit（GRU）

GRU的计算见式（10）。

式中：Xt为t时刻该层的输入变量；Rt为重置门，Zt为更新门；Ht为隐含状态；Ht-1为候选隐含状态；Wxr，Wxz，Wxh∈Rd×h和Whr，Whz，Whh∈Rh×h为权重参数；br，bz，bh∈R1×h为偏差参数；h为隐藏单元个数；d为输入变量维度；σ(x)和tanhx都是激活函数；⊙表示矩阵乘法。

1.3 ARMA模型预测噪声项

ARMA模型是时间序列预测的基本模型之一，利用ARMA模型预测噪声项。令Xt为t时刻的真实值，假设Xt不仅与t时刻之前的真实值Xt-1，Xt-2，…，Xt-p有关，还与t时刻之前的干扰值εt-1，εt-2，…，εt-q相关，则Xt可以用式（11）表示。

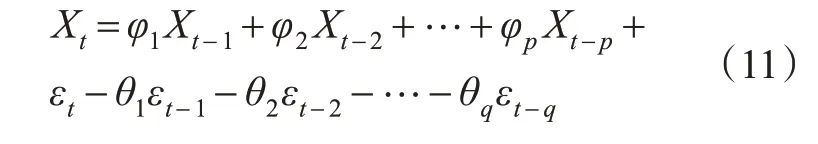
式中：φ1，φ2，…，φp与θ1，θ2，…，θq，均为该线性组合的系数。

要求Xt是平稳时间序列，εt是白噪声序列，且满足式（11）时，将{}Xt表示为p阶自回归与q阶滑动的结合序列，记为ARMA(p，q)。

式中：E是Xt的数学期望，[Var]是Xt的方差。

1.4 基于小波优化GRU-ARMA的预测模型

基于小波优化GRU-ARMA模型的空中交通流量短时预测的流程图见图2。首先利用小波变换将原始流量数据分解为不同频率的趋势项和噪声项，分别使用GRU神经网络模型和ARMA模型进行预测。将2个模型的预测结果叠加得到流量预测结果。

图2 基于小波优化GRU-ARMA模型的空中交通流量短时预测流程Fig.2 Short term air traffic flow frediction process based on Wavelet-Optimized GRU-ARMAmodel

1.5 评价指标

将小波优化GRU-ARMA模型预测值与真实值对比，对误差情况进行分析。本文选用均方根误差（RMSE）、平均绝对值误差（MAE）、平均绝对百分比误差（MAPE）作为误差评价指标，计算见式（13）～（15）。

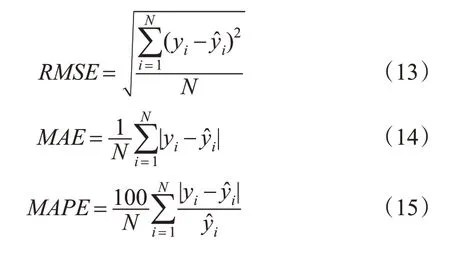
2 实例分析

2.1 数据说明

本文的数据来源于中国某终端区2019年4月29日—6月3日的ADS-B数据，共计36 d的数据，时间间隔取5 min，共10 368组数据。

2.2 小波变换分析

小波基函数及分解层数的选择没有明确的规则，多靠经验及实验结果确定。选择bior2.2，db3和sym4作为小波基函数，对原始流量数据进行3，4，5层的小波分解，信噪比计算结果见表1。由表1可见：在3种小波基函数不同分解层数的信噪比计算中，分解层数为3信噪比达到最大，信噪比越大，分解效果越好，说明分解层数设置为3时分解效果最好，所以在后续分析过程中，只考虑分解尺度为3的情况。

表1 不同分解层数信噪比对比Tab.1 Comparison of different decomposition layers of signal-to-noise ratio

分别选取小波基函数bior函数、db函数和sym函数对选取的终端区流量数据进行小波分解，计算相应的信噪比，根据信噪比计算结果选择最优的小波基函数，结果见图3。

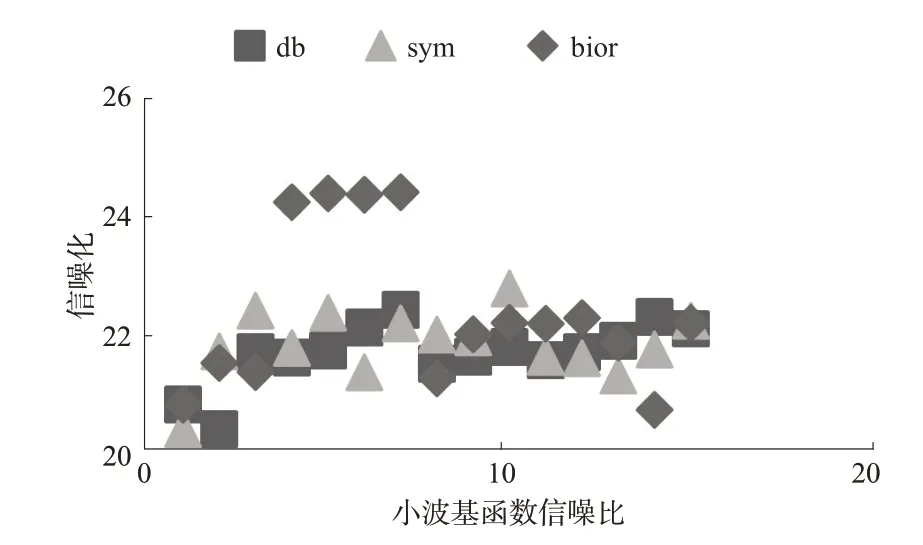
图3 小波基函数信噪比Fig.3 Signal noise ratio of wavelet basis function

根据信噪比计算结果，选定小波基函数bior2.8，分解层数为3，采用启发式阈值进行阈值处理，对原始流量时间序列进行小波分解处理，得到原始流量时间序列的近似序列和细节序列，结果见图4。

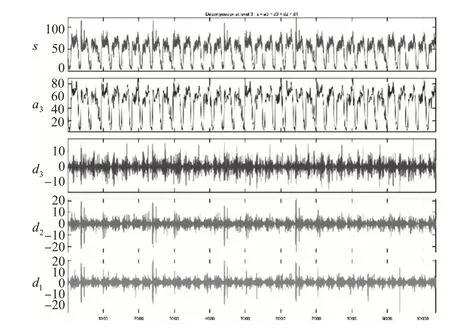
图4 原始流量时间序列小波分解图Fig.4 Wavelet decomposition of original traffic time series

2.3 GRU神经网络模型对趋势项进行预测

基于Python的keras神经网络库构建GRU神经网络模型，通过loss曲线（见图5）对模型进行诊断，batch size设置为64，迭代次数为500。小波分解处理过后得到的趋势项数据作为GRU神经网络模型的数据输入，将前30 d的以5 min为间隔的数据作为训练集，31～35 d的以5 min为间隔的数据作为测试集，对第36 d的前2 h流量进行预测，预测结果见图6。

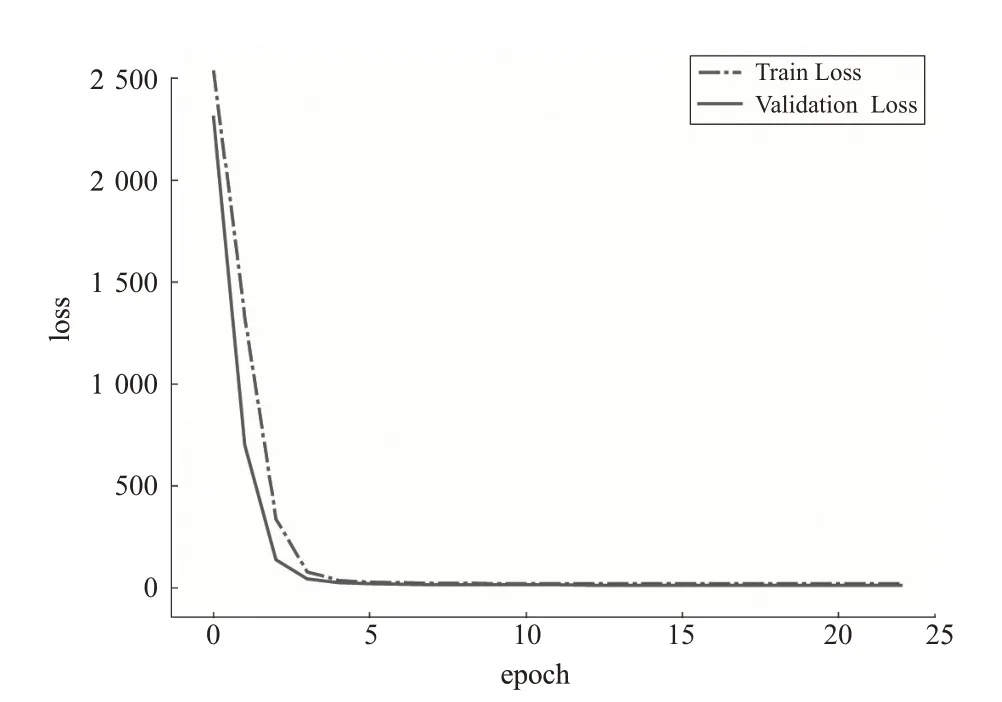
图5 GRU神经网络loss曲线图Fig.5 Loss graph of GRU

图6 趋势项预测结果Fig.6 Prediction results of trend items

2.4 ARMA（p，q）模型对噪声项预测

利用ARMA模型对噪声项进行预测，分为4个步骤。

1）数据平稳性检验。ARMA模型要求数据是平稳的，首先要对噪声项时间序列进行平稳性检验。本文使用增广迪基-富勒检验（ADF）单位根进行平稳性检验，通过Python中的adftest函数计算得到该噪声序列数据的ADF值为-5.360，见表2，该噪声序列在90%，95%，99%的置信区间下通过平稳性检验，说明可以使用ARMA模型。

表2 不同置信区间对应的临界ADF值Tab.2 Corresponding critical ADF value under different confidence intervals

2）模型定阶。根据贝叶斯信息准则（Bayesian information criterion，BIC）[20]绘制噪声项时间序列的热力图，见图7，当AR系数p设为4、MA系数q设为3时，BIC的值最小，对应方块的颜色是最深的，所以确定模型为ARMA（4，3）。

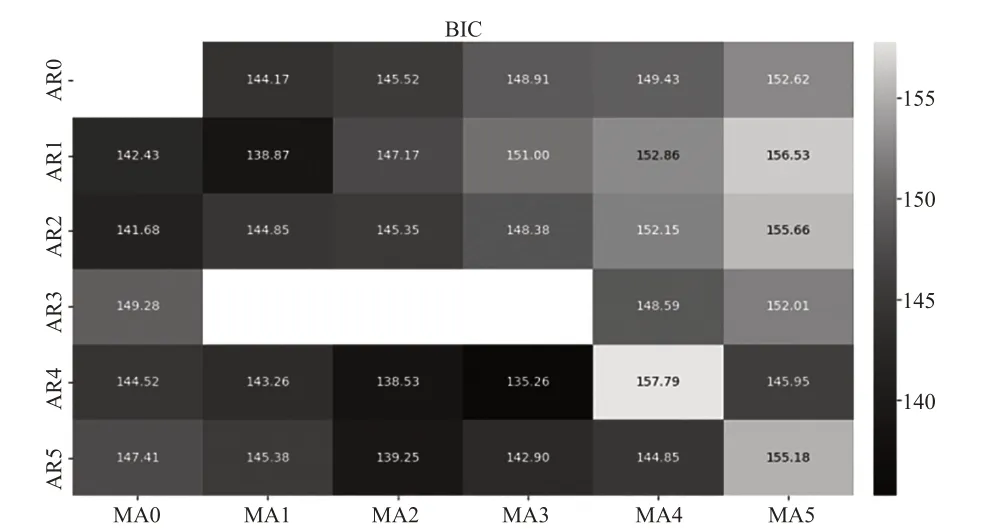
图7 噪声项ARMA定阶热力图Fig.7 ARMAthermal diagram of noise term

3）模型检验。为了确定ARMA模型的阶数适用于噪声项时间序列的预测，还需要对ARMA（4，3）模型进行进一步的残差验证。残差就是原始信号去除模型根据原始信息拟合出的信号后剩下的信号。如果残差是随机而且是正态分布的、不存在自相关情况的，就说明残差属于白噪声信号，也就代表了建立的ARMA（4，3）模型已经将所有有用的信号都包含了。本文利用Durbin-Watson[21]对残差进行检验，计算出的结果为2.006 5，这个值与2接近程度越高越说明残差通过检验，不存在相关性。

4）噪声项预测。噪声项的预测与趋势项的预测相对应，将10 368个噪声项数据分为864组，每组12个，将前680组数据作为训练数据，将第681～862组数据作为测试数据，对后2组数据值进行预测，得到噪声项预测结果。

2.5 总的流量预测

将GRU神经网络模型预测的趋势项数据和ARMA模型预测的噪声项数据叠加得到总的预测值，计算出每个预测点的相对误差，见图8。

图8 小波优化GRU-ARMA预测结果Fig.8 Prediction results of the wavelet-optimized GRU-ARMAmodel

1）不同模型对比。为了验证小波优化GRU-ARMA模型的预测效果及优越性，本文将小波优化GRU-ARMA模型、单一的GRU神经网络模型、BiLSTM模型、CNN-LSTM模型和ARMA模型的预测值与真实值进行对比，结果见图9。可以看出基于小波优化GRU-ARMA模型预测结果更接近真实值。

图9 不同模型预测结果Fig.9 Prediction results of different models

2）误差分析。为了进一步表明小波优化GRU-ARMA模型在真实值与预测值的接近程度相对于传统的神经网络模型和ARMA模型的优越性，本文对比了5种模型在预测每个点的相对误差，见图10。由图10可见：基于小波优化GRU-ARMA模型在每个点的相对误差基本都保持在2%左右，其他4种模型由于直接使用原始流量数据进行预测，每个点的误差都比较大，基本保持在5%～15%，GRU神经网络模型最大误差达到了28.57%，BiLSTM最大误差达到了37.14%，CNN-LSTM模型和ARMA模型最大误差达到34.29%，说明基于小波优化GRU-ARMA模型的组合模型预测效果相对于直接使用原始数据进行预测的模型更稳定。

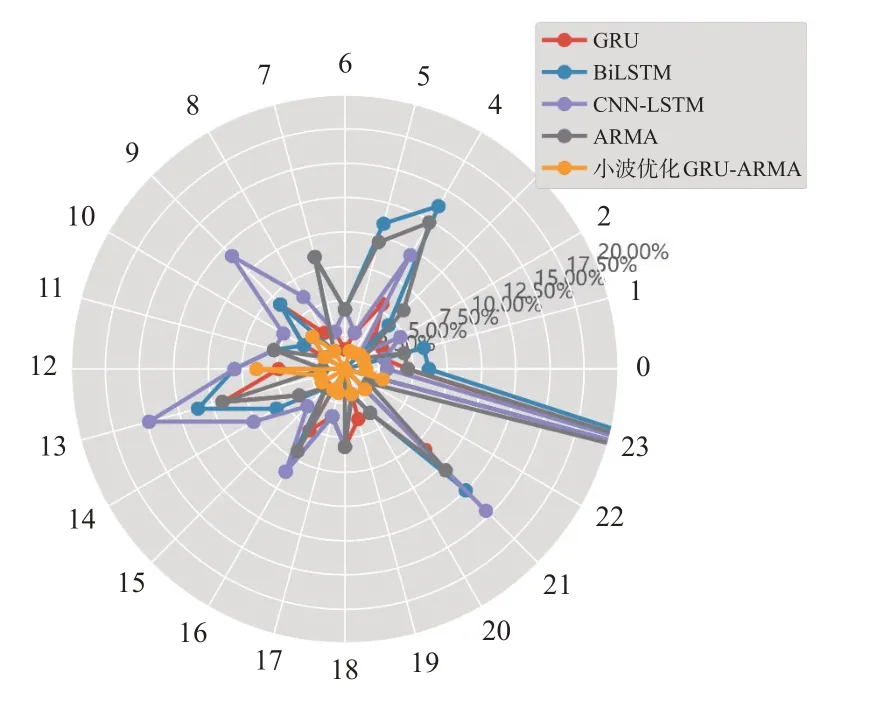
图10 5种模型误差对比Fig.10 Error comparison of five models

3）模型评价。计算5种模型的RMSE，MAE和MAPE，见表3。由表3可见：基于小波优化GRU-ARMA模型的预测精度最高，MAPE值为1.74%，与直接使用原始数据进行预测的GRU，BiLSTM，CNN-LSTM，ARMA模型相比，预测精度分别提高了3.02%，5.39%，5.05%，4.30%，更适合空中交通流量短时预测。

表3 5种模型的评价指标Tab.3 Evaluation indexes of four models

3 结束语

实验结果表明，基于小波优化GRU-ARMA模型的空中交通流量短时预测方法通过小波变换将原始流量数据分成不同频率的趋势项和噪声项2个部分，去除噪声的趋势项能够更好的反映空中交通流量的变化规律，使用了GRU神经网络模型对趋势项时间序列及ARMA模型对噪声项时间序列进行预测，结合2个模型的预测结果得到最终的预测值。实例分析表明：相比于直接采用原始数据进行预测的传统神经网络模型和单一的ARMA模型，基于小波优化的GRU-ARMA模型预测误差更小，解决了空中交通流量预测受随机因素干扰的影响，与直接使用原始数据进行预测的GRU，BiLSTM，CNN-LSTM，ARMA模型相比，预测效果更加理想，对于空中交通短时流量预测效果有所提升。

本文研究是对空中交通流量进行短时预测，未来将进一步，研究在多方面因素干扰下交通量的动态性预测，为空中交通动态管理提供依据。