考虑有限理性和公平性的危险品运输网络优化*

张宏刚 王伟 潘敏荣 刘志远▲

（1.东南大学交通学院 南京 211189；2.中国海洋大学经济学院 山东 青岛 266000；3.苏州规划设计研究院股份有限公司 江苏 苏州 215006）

0 引言

危险品具有特殊的理化性质，一旦发生事故，将会对沿线居民的生命安全构成巨大威胁[1]。2017年8月7日发生在滨州高新区的危化品车爆炸事故，造成5人死亡，11人受伤，直接经济损失约1 100万元；2020年6月13日发生在沈海高速公路的液化石油车爆炸事故，造成20人死亡，175人入院治疗，直接经济损失约9 477.8万元。为了从源头上控制风险，已有诸多学者针对危险品运输的网络优化问题进行了研究，提出了车辆限行和车辆收费2种管理策略。需要注意的是，传统的针对危险品运输网络优化问题的研究大多假设运输商是完全理性的，即遵循期望效用最大化原则。然而在交通运输领域，诸多研究均表明运输商的决策行为很难做到完全理性[2-3]，即决策者是为了找到一定范围内的满意解，而非绝对最优解，进而基于有限理性决策理论刻画出行特征。对此，有必要将有限理性决策理论应用于危险品运输网络优化研究中，充分地考虑运输商的决策心理和选择行为机理，可以更加合理准确地设计危险品运输网络。

在基于车辆限行的危险品运输网络研究中，2004年，Kara等[4]最先提出了1个双层整数线性规划模型来设计危险品运输网络。Sun等[5]讨论了风险不确定性，并基于鲁棒优化方法构建了双层规划模型。Taslimi等[6]分析了事故响应时间，并以最小化最大风险为目标构建了优化模型。Bianco等[7]以区域风险最小化为目标构建了网络优化模型。辛春林等[8]基于最小最大准则研究了危险品运输网络优化问题。

在基于车辆收费的危险品运输网络研究中，2009年，Marcotte等[9]首次提出了应用收费方案来引导运输商的路径选择，并构建了双层规划模型。Wang等[10]提出了1种双向收费模型来控制运输网络总风险。Bianco等[11]应用博弈理论来优化危险品运输网络。Assadipour等[12-13]基于收费策略研究了危险货物的多式联运网络设计问题。李奇等[14]探讨了时变条件下的危险品运输网络设计问题，以控制运输网络总风险。

然而，上述研究均假设运输商是完全理性的，即他们能够获得完全信息及进行无偏差估计，从而在进行决策时总是以总成本最小化为目标。但由于交通环境的不确定性及复杂性，决策者通常无法获取所需要的全部信息，使得他们在决策时很难做到完全理性。

基于上述分析，笔者在考虑有限理性的情形下，基于限行策略讨论了危险品运输网络优化问题。一方面，自从1955年Simon[15]首次提出有限理性的概念，并根据满意决策准则构建了选择行为模型以来，已有诸多学者将其应用于交通运输领域。Mahmassani等[16]基于满意决策准则讨论了出行者的路径选择行为。Lou等[17]进一步讨论了有限理性情形下的路径选择决策。可见，为了设计更加有效的危险品网络，有必要讨论有限理性决策者的路径选择行为对运输风险的影响，但上述针对危险品网络优化问题的研究均没有考虑运输商在有限理性情形下的路径选择决策。另一方面，Sun等[18]基于路段的感知偏差讨论了运输商的有限理性行为，但其没有考虑风险公平性问题，而该问题在实际运输过程中普遍存在，这主要是由于部分路段可能会被多次选择，使得这些路段周边的居民会承受更多的风险。虽然已有部分学者讨论了风险公平性问题，例如，Bianco等[11]基于车辆收费策略研究了带风险约束的危险品网络设计问题。王伟等[19]基于车辆限速策略，探讨了区域风险分布的公平性问题。虽然上述研究考虑了风险公平性问题，但同样没有结合有限理性进行分析，即均假设危险品运输商是完全理性的决策者。

本文讨论了风险公平性，并在考虑有限理性的情形下研究了危险品运输网络设计问题，建立了1个双层规划模型，上层规划表示政府通过关闭部分路段来控制风险，其目标是最小化总风险的最大值和路段最大风险上界值，以及最小化总的路段关闭数量，并为了实现公平性，增加了路段最大风险的上界约束；下层规划表示有限理性运输商在开放路段组成的路网中，以总成本最小为目标选择路径，设计了求解该模型的割平面算法。

1 有限理性的基本模型

针对网络最短路问题的研究，已有诸多学者提出了完全理性情形下的最短路模型，见式（1）。

式中：C为完全理性情形下的最小总成本；cij为路段(i，j)的成本；xij为0-1决策变量，当运输商选择路段(i，j)时取值为1，否则，取值为0。

然而，由于运输环境的复杂性及不完全信息的存在，使得运输商往往是有限理性的决策者，即他们选择的不是最优而是满意路径，见式（2）。

式（2）表示有限理性运输商的路径选择决策，即当路径的总成本不大于(1 +k)C时，运输商就会选择该满意路径，其中，k∈[0，1)为常数，表示运输商的有限理性强度。

Sun等[18]进一步基于感知偏差（Perception Error，PE），提出了针对有限理性决策者的网络最短路模型，见式（3）。

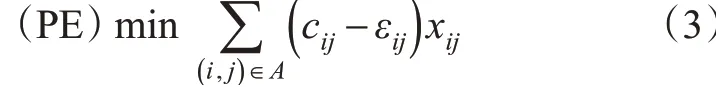
式中；εij为运输商对于路段(i，j)上运输成本的感知偏差，其取值在1个给定的感知偏差集合ξ内，而ξ的计算见式（4）。

同时，Sun等也证明了在给定感知偏差的集合ξ时，PE模型和MS模型是等价的，并得到了如下定理。

定理1。在给定一系列感知偏差εˉ∈ξ时，得到PE模型的最优解xˉ，同时也是MS模型的满意解，即

Sun等对定理1给出了严格的理论证明，其主要阐述了MS模型和PE模型的等价性，即可以通过求解MS模型得到满意解，也就是PE模型的最优解，这在一定程度上解决了PE模型求解难度较大的难题，为后文构建的危险品网络优化模型的求解提供了理论支撑。

2 问题描述与模型构建

2.1 问题描述

设G(N，A)为危险品运输网络。其中：N和A分别为节点集合和路段集合。假设有某种危险品需要从起点O运输至终点D，政府为了控制运输风险，首先决定关闭部分路段，同时考虑到运输商是有限理性的，设定了其感知偏差的集合。由于部分路段可能会被危险品运输车辆多次选择，从而造成风险分布的不公平性问题，为了实现公平性，增加了路段最大风险的上界约束来影响运输商的路径选择决策。政府目标是最小化总风险的最大值和路段最大风险上界值，此外，为了避免关闭较多不必要的路段，政府部门同时会以总的路段关闭数量最小化为决策目标。然后，运输商在考虑感知偏差的情形下，在开放路段组成的路网中选择总成本最小的路径。最后，运输商将路径选择信息反馈给政府部门，而政府部门根据反馈信息对决策做出调整，双方的博弈决策过程见图1。

图1 危险品运输网络优化模型Fig.1 The model of hazmat transportation network optimization

2.2 符号及变量说明

符号及变量说明见表1。

表1 符号说明Tab.1 Thesymbol table

2.3 模型构建

为了简化研究，作如下假设。

1）运输风险只和危险品车辆数、沿线人口密度有关。

2）在危险品运输过程中，风险的表征主要和危险品车辆有关，虽然社会车辆也存在一定的暴露，但在一定范围内数量有限，且不会完全暴露，暂不予考虑。

为了测量风险公平性，选取方差系数γ和基尼系数ω作为指标[20-21]，其计算见式（5）和式（6）。

考虑有限理性和公平性的危险品运输网络优化模型如下。

上层规划模型见式（7）～（10）。

下层规划模型见式（11）～（14）。

其中：式（7）为政府目标，即最小化总风险最大值、总路段关闭数量以及路段最大风险上界值；式（8）为路段最大风险的约束条件；式（9）为上层决策变量，当yij取值为1时，表示政府决定路段(i，j)可以被运输商使用，反之，则表示政府关闭路段(i，j)；式（10）确保了运输商的感知偏差在给定的集合内，通常情况下，感知偏差ξs的集合见式（15）；式（11）为运输商在考虑感知偏差的情形下选择总成本最小的路径；式（12）为流量守恒式，确保了危险品从起点运输至终点；式（13）为运输商只能选择开放的路段进行运输；式（14）为下层决策变量，当运输商选择路段(i，j)时取值为1，否则取值为0。

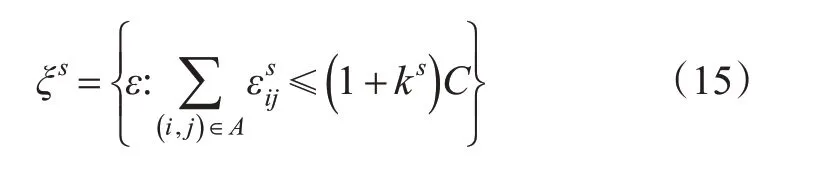
式中：C为完全理性情形下的最小总成本，在考虑政府相关决策(yij)的前提下，可得

式中：为0-1决策变量，对于第s种流向，运输商选择路段(i，j)时取值为1，否则，取值为0。

3 模型求解算法

针对双层规划模型的求解，已有诸多启发式算法被应用[22]，而上述模型是1个含有3层结构的危险品运输网络优化模型，其中，最下层是1个完全理性情形下的最短路模型。对此，重新定义了外层问题（out-layer problem，OLP）和内层问题（inner-layer problem，ILP），并设计了求解该模型的割平面算法[18,23]，最后，经过不断迭代求解内、外层问题达到博弈均衡。

3.1 外层问题

外层问题（OLP）描述了政府的决策（y），即通过实施路段限行策略来最小化运输网络的最大总风险和路段最大风险的上界值以及总的路段关闭数量，同时，本文应用了线性加权法来处理双目标，则OLP的基本模型见式（20）～（25）。

3.2 内层问题

内层问题（ILP）描述了运输商的决策(x)，通过求解外层问题（OLP）可以得到由开放的路段组成的运输网络，然后，运输商在考虑感知偏差ξs集合的条件下选择可行路径，进而选定使得运输网络总风险最大的运输路径，则ILP的基本模型见式（26）～（31）。

由于内层问题是1个双层规划，针对该模型的求解同样属于NP-hard问题，其中，下层规划为有限理性决策者的路径选择模型，其和上文提到的PE模型（即式）本质一致，而上层规划的目标是最大化运输网络总风险，其决策变量是运输成本的感知偏差。根据定理1，设计了解析式算法求解上述双层规划模型：在上层规划给定一系列感知偏差εˉ∈ξ的条件下，PE模型的最优解xˉ和MS模型的满意解一致，所以可根据K-最短路算法产生一系列成本不大于(1 +ks)c0的运输路径，即为下层规划的最优解；接着，下层将路径选择信息反馈给上层，而上层选择使得运输网络总风险最大的运输路径（或者说感知偏差的取值），即为上层规划的最优解，上、下层之间反复博弈，达到博弈均衡状态时停止，从而得到内层问题（ILP）的最优解。

3.3 求解步骤

步骤1。令迭代次数t=1。

步骤2。通过求解外层问题（OLP），得到最优解和。

步骤3。将求解得到的最优解作为已知参数代入内层问题（ILP），并求解ILP得到最优解。

步骤4。比较最优解和̂，如果二者一致，则停止；否则，根据Gzara[23]提出的割平面算法增加新的约束条件到外层问题，并令t=t+1，返回步骤2。

4 算例分析

为了验证本文提出的模型和算法的有效性，以领域内常用的Nguyen-Dupuis网络为例进行分析[24-25]，见图2。假设有某种危险品需要从节点1和4运往节点3和2，各流向所需车辆数为d1=2和d2=3，依据文献[18]设定转换系数α=0.025，参数k1=k2=0.1，各路段属性值见表2。然后，基于人口覆盖率模型[26]，主要以路段两侧的人口密度来定量刻画运输风险。

表2 路段运输成本和沿线人口密度Tab.2 Travel costof each link and population density along the line

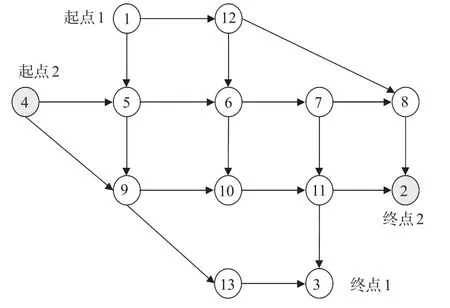
图2 危险品运输网络Fig.2 Hazmat transportation network

通过求解上述模型，可以得到不同权重λ取值，危险品运输网络的优化结果见表3～6和图3～5。

由表3～6可见：在考虑有限理性的情形下，不同λ取值时危险品网络的优化结果存在显著差异，例如，λ=0.2时，政府为了控制运输网络的最大总风险，会选择关闭路段(5，6)和(1 3，3)；而当λ=0.8时，政府部门会选择关闭路段(5，6)和(5，9)。同时，运输商在考虑感知偏差的情形下，在开放路段组成的路网中选择运输路径（见表6），可以看到，不同λ取值时运输商的可选路径也存在差异，而且随λ取值的增大，网络总风险的最大值会有所下降，尤其当λ取值为1.0时，网络总风险的最大值的变化幅度较大（相比于λ取值为0.4而言），其原因是运输网络的最大总风险对上层规划的影响会逐渐增大。

表3 危险品运输网络的优化结果（λ=0， 0.2， 0.4， 0.6）Tab.3 Optimization results of hazmat transportation network(λ=0， 0.2， 0.4， 0.6)

表4 危险品运输网络的优化结果（λ=0.8）Tab.4 Optimization results of hazmat transportation network(λ=0.8)

表5 危险品运输网络的优化结果（λ=1.0）Tab.5 Optimization results of hazmat transportation network(λ=1.0)

表6 不同权重取值时，优化后各流向的可行路径Tab.6 The feasible paths for each shipment after optimization at different weights

当政府不实施车辆限行策略时，运输商在考虑感知偏差情形下的路径选择结果见图3，此时运输网络的最大总风险为3 456，相较于政府实施车辆限行策略后的网络总风险的最大值增加了8.4%（以λ=0.4为例）。可见，在考虑有限理性的情形下，政府部门通过实施车辆限行策略来控制网络总风险是有效可行的。

图3 优化前各流向的可行路径Fig.3 The feasible paths for each shipment before optimization

由图4可见：在考虑公平性约束的情形下，方差系数和基尼系数均会明显地降低，这说明通过增加各路段最大风险值的上界约束可以有效地实现不同路段之间风险分布公平性的目标，其原因在于该策略可以影响运输商的路径选择，从而达到风险分布公平性的目的。值得注意的是，当λ=1时，有无该约束条件时的方差系数和基尼系数一致，其原因是政府仅以最大总风险的最小化为目标，所以增加的各路段最大风险的约束条件（即式（9））将不会对优化结果产生影响，即有无公平性约束时的优化结果相同。

图4 公平性约束有无情况下不同λ取值时的方差系数和基尼系数Fig.4 The coefficient of variance and Gini coefficient at different values of λ with and without fairness constraint

由图5可见：对于任意的权重λ和参数k（令k=k1=k2），在考虑有限理性的情形下，实施车辆限行策略后的最大总风险的最小值均明显小于不实施车辆限行策略时的风险值，这说明通过实施该方案可以有效地控制网络总风险的最大值。当政府不实施车辆限行策略时，随k取值的增大，最大总风险的最小值呈上升趋势，其原因是随k的增加，有限理性运输商可以选择的运输路径会随之增加。当政府实施限行策略时，最大总风险的最小值不会随k取值的变化而变化，但关闭路段的数量会随k取值的增加而增加，其原因是政府总是以总风险最小化为目标，所以当运输商可选择的运输路径增加时（即k取值的增加），政府为了达到降低运输网络最大总风险的目的会选择关闭更多的路段。

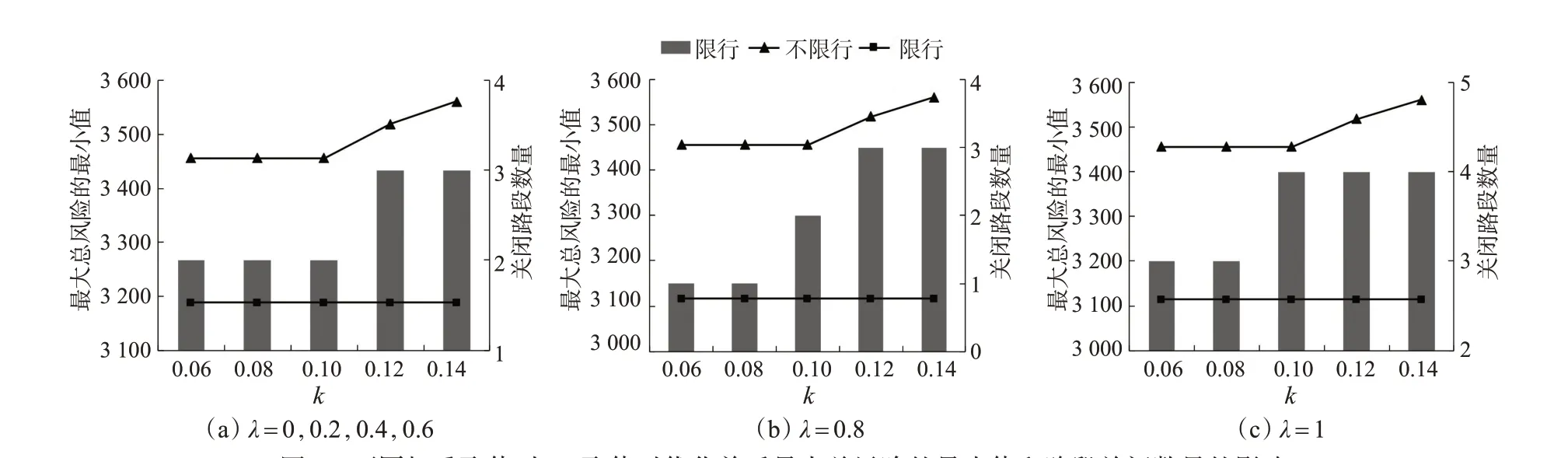
图5 不同权重取值时，k取值对优化前后最大总风险的最小值和路段关闭数量的影响Fig.5 Effect of k on the minimum value of the maximum total risk and the number of link closures before and after optimization at different weights

5 结束语

在考虑有限理性的情形下，提出的设计危险品运输网络的新方法考虑了风险公平性问题，能够降低网络总风险的最大值，保证不同路段之间的风险公平性；政府部门通过改变对各目标的关注度，可以得到不同的网络优化方案；探讨了有限理性运输商的感知偏差的变化对运输网络总风险的影响，发现感知偏差的变化并不会对运输网络最大总风险的最小值产生影响，而会改变总的路段关闭数量；虽然关闭部分路段会降低整个运输网络的利用率，但可以极大地降低运输网络的总风险。在考虑运输商为有限理性决策者的前提下，研究了危险品运输网络设计问题，更加符合实际运输情况，所以政府部门在对危险品运输网络管理时可以进一步考虑运输商的有限理性行为，从而设计更加合理有效的危险品运输网络，进而缓解交通事故的发生并提高社会整体经济效益。

后续研究将进一步讨论时变条件、随机需求、社会车辆和危险品车辆混行等更多实际因素对危险品运输网络优化问题的影响。