高速铁路轮轨电弧烧损绝缘节的研究
2022-09-15苏鹏飞
苏鹏飞,谭 丽,温 润
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2.西北民族大学 电气工程学院,甘肃 兰州 730030)
我国高速铁路开通以来,在高铁站内多次出现绝缘节烧损现象,由于高铁运营组织的要求,很难就这一问题进行现场实际测试,通过远距离拍摄的照片和录像发现,其共性是绝缘节烧损地点均在侧线空扼流变压器中心未进行连接,即牵引回流切断点(又称“一头堵”)的区段;时间通常在发车条件下。动车组前部和中部轮对经过绝缘节时,在轮轨接触位置可观测到放电拉弧现象。
针对轮轨电弧烧损绝缘节问题,国内学者进行了诸多研究。文献[1]利用真实的钢轨模拟列车运行场景,复现绝缘节烧损现象,确定了由于轮轨间出现电弧造成绝缘节的烧损。文献[2]通过分析轨道回归电流数据,认为在切断点处,牵引电流切换流向导致电流瞬间断开,造成轮对与钢轨侧发生切断拉弧是发生绝缘节烧损的主要原因。文献[3]通过将原有的“一头断”改为两边绝缘节均为回流断点的“两头堵”方式,并增加回流通道,达到降低绝缘节两端电位差的目的。文献[4]对电弧进行等级划分,认为较高等级的电弧对绝缘节的灼伤更严重,且发现电弧持续时间对绝缘节的烧损程度也有一定的影响,并提出了改进措施。但上述文献并未对轮轨电弧温度进行详细的计算,也未计算绝缘节在不同温度下的材料相变程度,因此无法确定不同等级电弧对绝缘节的烧损程度。
对此,本文通过接触斑点上的电流密度确定电流分布,综合接触斑点带来的接触电阻计算轮轨接触斑点上的电压分布,确定电压最大值点为电弧两极的具体坐标,确定不同电压等级电弧带来的温度具体数值,根据绝缘节材料的相变函数确定不同等级电弧对绝缘节的烧损程度。
1 轮轨电弧电压计算
1.1 接触斑电流分布方程
当电流流经接触斑点时,由于轮轨表面存在趋肤效应,接触斑点上的电流密度分布并不是均匀的。轮轨接触电流密度分布直接影响轮轨电弧的电压等级,所以为了准确分析绝缘节烧损问题,需首先对轮轨电流密度分布进行计算。
本文依据钢轨轨面建立三维坐标系,如图1所示。X1轴正方向指向列车运行前方;X2轴正方向垂直于列车运行方向并指向轮缘方向;X3轴正方向垂直于轨面向上,原点坐标为钢轨轨头中心位置。利用1 mm×1 mm的矩形单元对不规则的接触斑进行离散化,类比非Hertz接触理论计算模型[5],建立轮轨接触斑点上的电流密度方程。
通过对接触斑进行离散化,建立接触斑上的电流密度分布方程为
( 1 )
式中:WJτ为轮轨间的刚性滑动量;uJτ为轮轨间的弹性位移量;qJτ为轮轨间电流密度;Ac为全部矩形单元;A0为矩形单元面积;C为电流密度;q为每个接触斑内通过的电流密度;i,j=1,2,3,为坐标轴3个方向;qji为单元J上的电流沿i轴的流动分量;hJ为轮轨接触面之间的法向间隙在单元J中心处的分量;a为轮轨在X3方向的弹性压缩量,通过几何计算确定;AIiJj为影响系数;QN为电流密度总值。
由于轮轨材料的高度相似,其本构模型的差异可以忽略不计,故可将式( 1 )简化为式( 2 ),并引入Lagrange乘子λ列出式( 2 )的Kuhn-Tucker条件,利用牛顿拉夫逊法(Newton-Raphson)对Kuhn-Tucker方程组进行迭代求解,计算出电流密度分布函数。
( 2 )
引入Lagrange乘子λ列出式( 2 )的Kuhn-Tucker条件为
( 3 )
式中:hM为计算系数。
由式( 3 )计算得出接触斑内的电流密度最大值点。电流与电流密度的关系为
( 4 )
式中:I为总电流值;Ji为电流密度;S为接触斑面积。综合式( 3 )和式( 4 )即可确定流经接触斑的总电流值。
1.2 接触斑接触电阻计算
由于牵引回流电流通过轮对流向钢轨,在轮轨接触斑点上的电流通路仅为发生真实接触的微凸体,电流经过的真实接触面积为各微凸体接触面积的总和,通路有效导电截面瞬间减小,导致电流线收缩,此时将接触斑收缩电流线的现象等效为接触表面存在收缩电阻。当轮轨接触斑点上存在沙石、铁锈等导电性差的杂质时,接触斑点上除了收缩电阻,还存在膜电阻,但由于高铁列车的质量大,速度高,且车站内作业量大,钢轨轨面几乎不存在杂质,所以本文不考虑膜电阻。接触电阻与接触面积和电阻率的函数关系为[6-7]
( 5 )
式中:Sa为接触斑点的宏观接触面积;Sr为轮轨真实接触面积;轮轨电阻率ρ=2.1×10-7Ω·m。通过模拟计算发现轮轨接触斑为不规则的斑点,为便于计算,在不影响计算结果的条件下,将不规则的接触斑按面积等效为圆形。真实接触斑圆的半径r计算公式为
( 6 )
式中:n为Hertz接触理论规定的接触系数;N为接触斑上的法向载荷;k1为车轮的材料常数;k2为钢轨的材料常数,材料常数与物体材料的弹性模量和泊松比有关;A、B为轮轨间初始间隙函数的常数。
根据电弧电压值的大小将轮轨电弧进行分级,见表1。
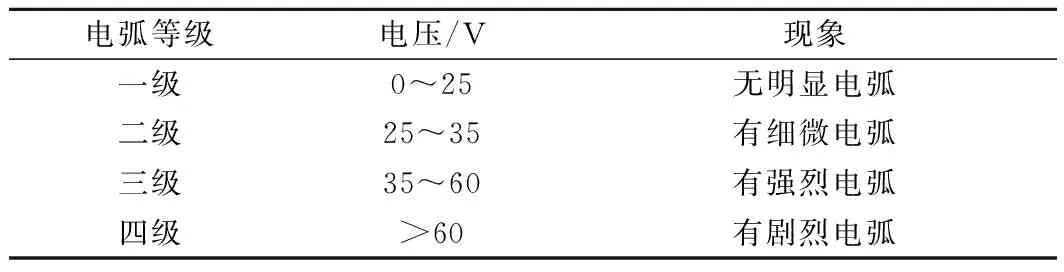
表1 轮轨电弧等级划分
2 轮轨电弧烧损绝缘节
2.1 电弧温度场的确定
在高铁轮对经过切断点绝缘节时,钢轨上牵引回流电流的流向会从流向列车运行后方的钢轨瞬间改变为流向列车运行前方的钢轨,此时,列车运行后方钢轨与轮对之间的电流通路瞬间切断,会在车轮踏面和轮对离去的钢轨轨头之间产生切断电弧,电弧的高温直接影响绝缘节的绝缘性能变化,通过确定电弧温度场,可以准确分析绝缘节在不同温度场中的受热导致材料相变的程度,从而确定绝缘节烧损的不同程度。所以确定电弧温度分布情况是计算绝缘节受热导致烧损的基础。
首先需以钢轨轨面中心点为原点,以钢轨延伸方向为X轴,以垂直于钢轨轨面竖直向上方向为Y轴,以垂直于钢轨延伸方向为Z轴建立三维坐标系,以此为基础建立轮轨分离点的运动轨迹方程,在考虑轮轨横移量的条件下,计算三维空间内电弧阴极运动轨迹。
( 7 )
式中:x、y、z为轮踏面上轮轨分离点在三维坐标系中的位置;t为时间;r为车轮半径;θ为车轮半径所经过的角度。式( 7 )描述了车轮与钢轨接触的最后一个分离点在经过绝缘节时的运动轨迹,通过计算该点的运动轨迹可以确定在电弧持续时间内电弧两极位置的变化情况。
根据电弧温度场与热流密度的紧密联系,并查阅电弧相关研究[8-13],确定轮轨电弧相关分析指标,建立轮轨电弧温度场正态径向分布模型
(8)
Qarc=ηaUI
(9)
(10)
式中:q(r)arc为电弧热流密度;K为热流集中系数;Qarc为电弧有效热功率;r为电弧周围某点距电弧中心的距离;U为电弧电压;I为电弧电流;ηa为电弧有效利用系数,取0.75;a为热流集中系数常数;δq为电弧热流分布参数,本文中,a、δq均取3。
综上分析计算可得轮轨电弧热流分布模型为
(11)
2.2 绝缘节烧损计算
列车在经过绝缘节时的速度直接决定了轮轨电弧的持续时间,列车运行速度越高,电弧持续时间就越短,但同时,维持列车的高速运行必然需要更大的牵引电流,此时轮轨电弧虽然持续时间短,但由于弧压等级较高,电弧所带的温度也会是低等级电弧的数倍,高铁发车时的列车牵引等级共分为十级,分别对应着不同大小的牵引电流,文献[4]中,虽然就牵引档位对电弧的影响进行了讨论,但没有详细计算电弧造成的高温。所以无法准确模拟绝缘节的烧损情况。
高铁站内采用的是环氧酚醛树脂所制作的胶粘绝缘节,胶粘绝缘节的熔点约为393.5 K,碳化温度在573.5 K左右,绝缘节在1 073.5 K时碳化率达到70%,而钢轨的熔点约为1 773.5 K,绝缘节易发生烧损现象。当轮轨在绝缘节处有电弧发生时,绝缘节正处在电弧的高温场中,电弧通过辐射散热将热量传递给绝缘节。电弧的高温使得绝缘节材料发生性能相变,绝缘节材料转变相率公式为
(12)
式中:Tm为碳相线和固相线的温度平均值;ε为碳相线和固相线温度差值的一半。固相的固化温度Ts、碳相的碳化温度TL分别为平均温度加减ε。
通过计算绝缘节碳化率即可确定不同等级电弧对绝缘节的烧损程度。
3 仿真结果分析
在列车轴重为9 t、无横移量的轮轨接触条件下,利用建立的模型分析求解不同电流在接触斑上的电流密度分布情况,并根据电流密度的大小确定相应电流作用下轮轨电弧温度分布情况。分析确定不同等级电弧作用下绝缘节绝缘性能变化的函数,从而得到绝缘节烧损的数学模型。
3.1 接触斑电流分布
由于列车接地方式的不同,造成轮轨接触斑点上的泄放电流有较大的变化,为了便于计算,本文将不规则的接触斑点先等效为圆形,利用1 mm×1 mm的矩形单元对圆形接触斑进行离散化,建立轮轨接触班上的电流分布方程,并给出电流密度初值,带入式( 3 ),利用牛顿拉夫逊法对Kuhn-Tucker方程组进行迭代求解,接触斑上沿某一半径的电流密度初值见表2。
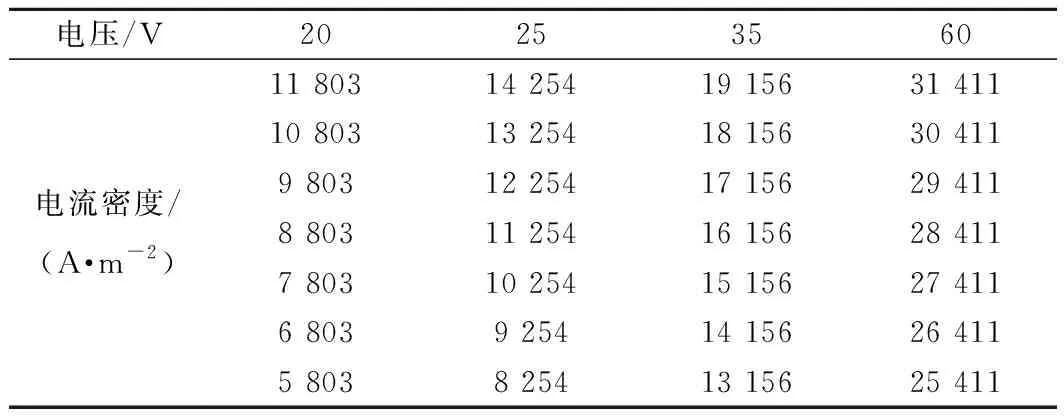
表2 接触斑中心处电流密度初值
通过求解每个单元上的电流密度,确定接触斑点整体的电流密度分布,表3给出了不同电流流经接触斑点时,接触斑中心处的电流密度,当61 A的电流流经接触斑点时,最大电流密度值出现在接触斑点中心处,为9 738.9 A/m2;当列车通过轮轨泄放的电流达到85 A时,中心单元的电流密度达到12 265 A/m2,这主要是因为在接触斑中心处轮轨实际接触面积最大,所以流经该实际接触斑点的电流也最大。

表3 不同电流作用下的接触斑中心处电流密度
根据电弧产生的条件可知,在大气中开断电路时,只要电压超过12~20 V,被开断的电流若超过0.25~1 A,在触头间隙就会产生电弧。图2为产生不同电压等级电弧时,接触斑点上的电流密度分布情况。因为本文将轮轨接触斑点等效为圆形,又用1 mm×1 mm的矩形单元对圆形接触斑进行离散化,所以由图2可以看到,在11 mm×11 mm的矩形内,电流密度的分布基本为圆形,可以发现轮轨接触斑点中心的电流密度最高,相应地会在中心处产生较高的电压。
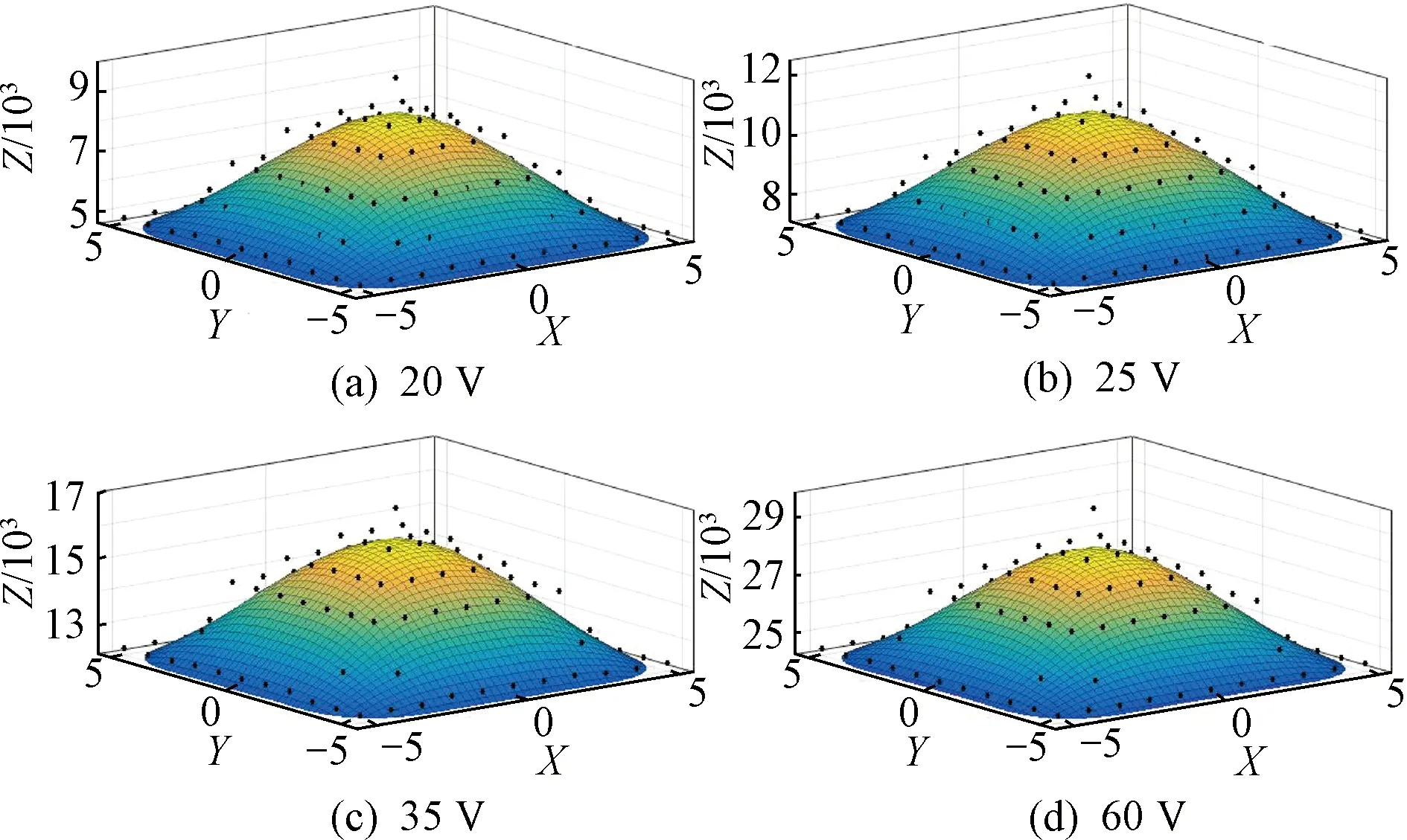
图2 接触斑电流密度分布
3.2 接触电阻计算
表4为不同轴重下的轮轨接触面积。根据电接触理论的计算方法[14-15],综合Hertz接触理论计算出的真实接触面积Sr和有限元计算出的宏观接触面积Sa,利用电接触理论中接触电阻计算方法,求解得出不同轴重条件下的轮轨接触电阻的具体阻值。当轴重为9 t时,真实接触面积为46 mm2,宏观接触面积为98 mm2,将其代入式( 5 ),计算此时轮轨接触电阻为2.03×10-5Ω。

表4 不同轴重下的轮轨接触面积
图3显示了不同轴重下轮轨接触电阻的变化。可以看到,当轴重增加时,轮轨接触电阻呈减小趋势。这是由于轴重增加时,微观上轮轨表面上较高的微凸体由于发生了塑性形变,导致较矮的微凸体也发生了接触,此时接触斑内发生接触的微凸体数量也相应增加,轮轨间有效导电斑点数目相应增多。此时,接触斑收缩电流线的能力由于接触斑点的增多而下降,宏观上反映出轮轨接触电阻呈下降趋势。
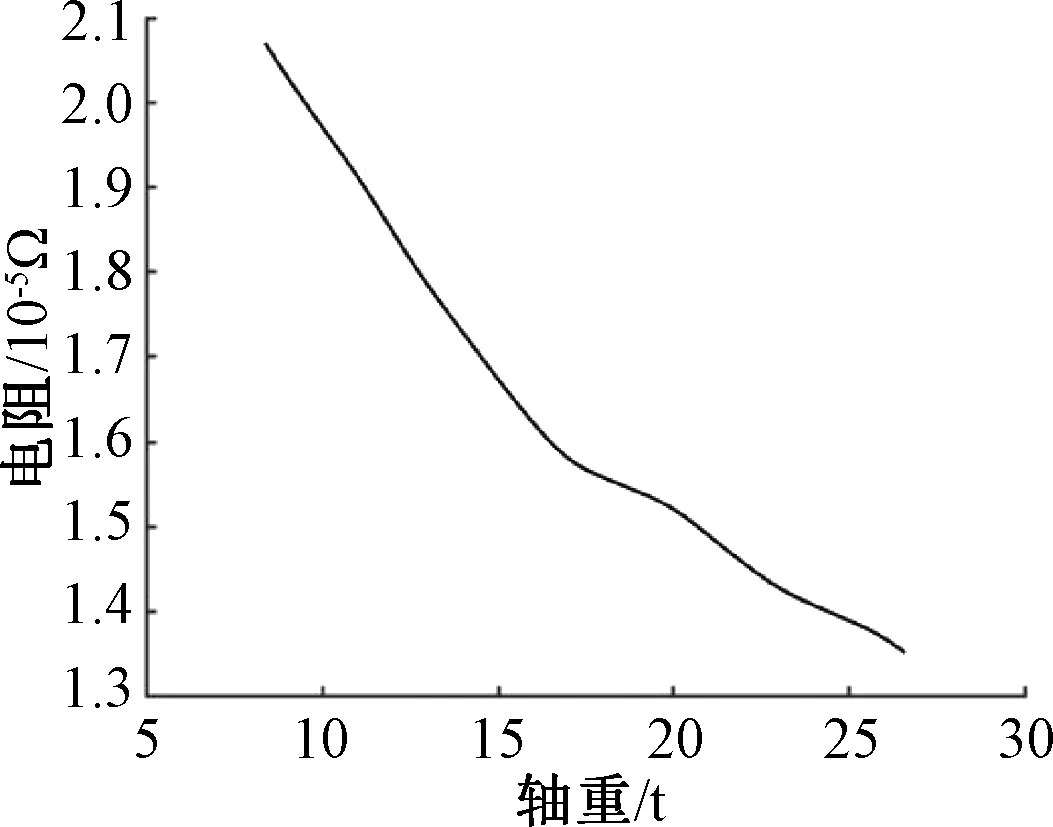
图3 接触电阻变化趋势
由于本文利用1 mm×1 mm的矩形单元对圆形接触斑进行离散化,并且要计算每个单元上的电压大小,所以首先要计算出每个单元的电阻大小。在列车轴重增加时,由于已经达到轮轨材料的极限变形,中心单元接触面积并没有较大的变化,因此中心单元接触电阻基本不变。可计算得到当列车轴重为9 t时,接触斑点中心处接触单元电阻约为2.0×10-3Ω。综合图2接触斑电流密度分布结果及接触电阻的计算结果,可得不同电流作用下的轮轨电压,见表5。

表5 不同电流作用下的轮轨电压
3.3 电弧温度场的确定
在轮轨电弧持续的时间内,车轮依旧向前运行,所以轮轨电弧将被拉长,电弧的两极位置也随着列车的移动而改变。由于绝缘节烧损情况主要发生在侧线空扼流变压器中心未进行连接,即牵引回流切断点处,所以当列车经过切断点绝缘节处时,轮轨之间肯定会出现或多或少的横移量。
本文假设在轮轨电弧持续时间内,列车向前移动伴有8 mm的横移量,即车轮中心偏离钢轨中心8 mm,以此建立电弧位置函数式( 7 ),通过求解式( 7 ),可以得到在电弧持续时间内,轮轨电弧阳极位置的变化情况。图4即为列车车轮旋转一周时间内阳极位置变化,x轴为钢轨延申方向,y轴为垂直于钢轨延伸方向向上,z轴为水平面上垂直于钢轨延伸的方向。由图4可知,在轮轨电弧持续时间内,电弧阳极的运动是按照一个带有偏移量的“摆线”运动的。随着电弧阳极位置的运动,电弧被拉长,绝缘节在电弧温度场中所处的位置也在变化,绝缘节所受到的温度也有所不同,所以根据电弧阳极位置的变化可以分析绝缘节处受热情况。
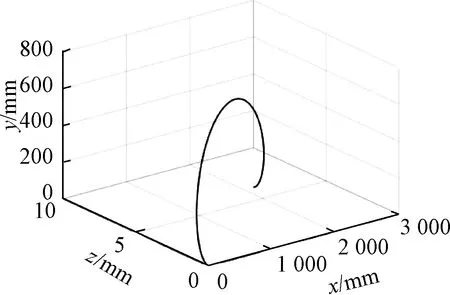
图4 轮轨电弧阳极位置
由式(11)可知,在不同电弧电压、电流条件下产生的电弧,其温度在空间中具有正态分布的特点,本文选取20.0、27.7、43.1、74.4、80.77 V电压的电弧进行进一步的分析计算,计算结果如图5所示。结果表明,在同样的环境条件下,电压等级越高,该电弧产生的温度越高。20 V电压所产生的电弧中心温度仅有97 K,说明20 V时不产生电弧。但80.77 V电弧的中心温度已达到1.587 6×103K的高温。
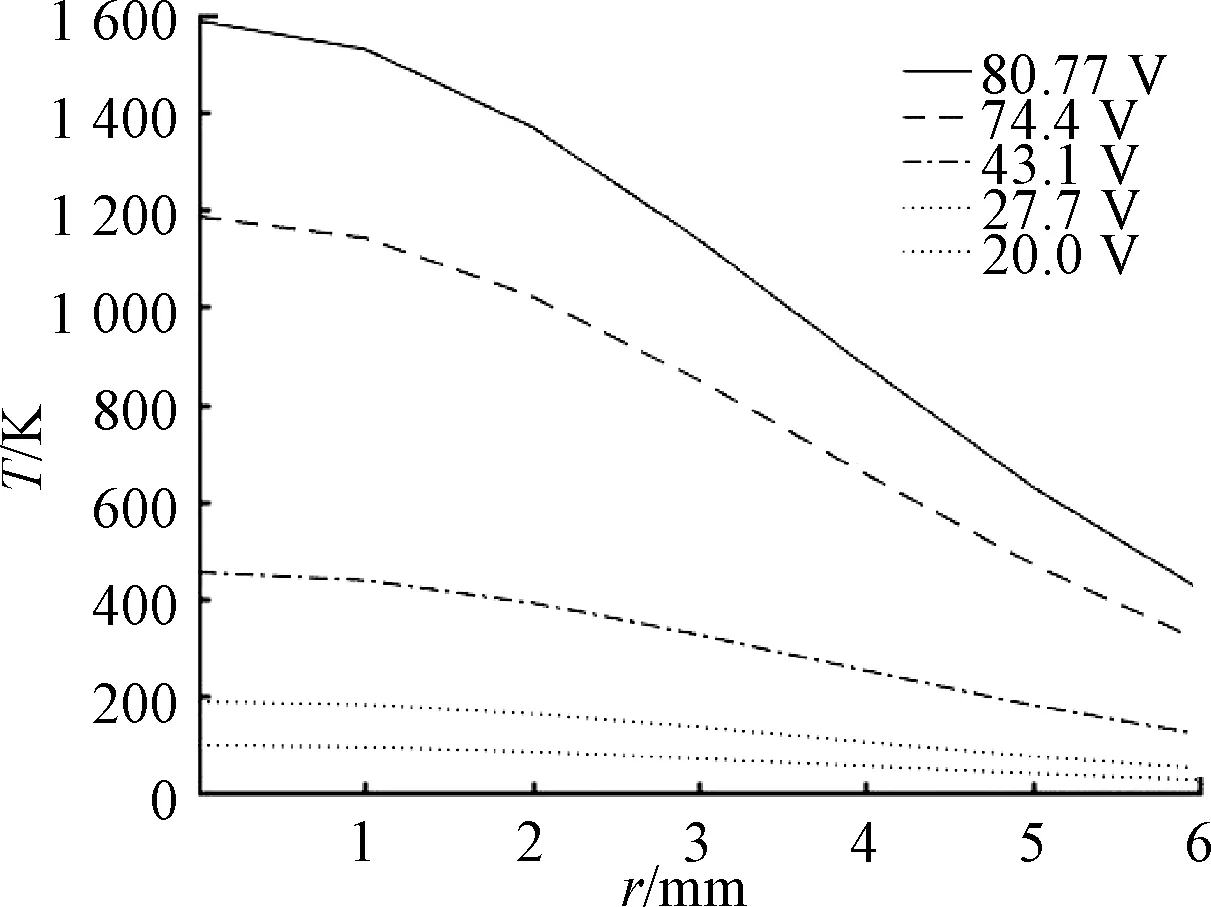
图5 轮轨电弧温度分布
3.4 绝缘节烧损计算
通过查询绝缘节材料标准,可知绝缘节胶粘绝缘节的熔点为393.5 K,碳化温度在573.5 K左右。绝缘节碳化过程是由其碳化温度确定的,而多组分的物质发生相变时,从碳出现在材料表面的温度开始,到最后一种组分固体碳化的温度为止,是物质发生相变的整个温度范围[16-17],据此,建立绝缘节在不同温度下碳化率的变化(式(12)),计算结果如图6所示。
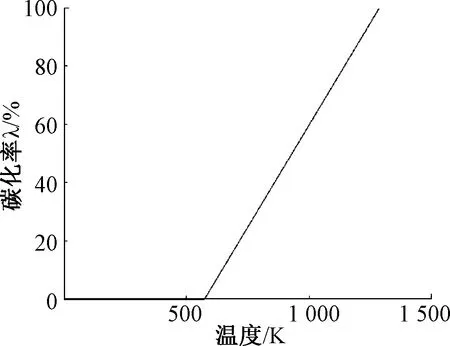
图6 绝缘节碳化率
由图6可知,当绝缘节受到的温度达到573.15 K时,绝缘节开始发生碳化,温度在573.15~1 287.15 K之间,绝缘节碳化程度逐渐加剧,当绝缘节受到的温度达到1 287.15 K时,绝缘节全部碳化,这就说明绝缘节的碳化是一个量变的过程,碳化率的大小直接决定了绝缘节的绝缘性能,只有当绝缘节的碳化率超过某一临界值,即多次电弧高温作用绝缘节后,才会出现轨道电路红光带。
本文以绝缘节距电弧中心距离为2 mm进行分析,综合图5、图6,可分析得出在不同等级电弧下,绝缘节的碳化率,见表6。
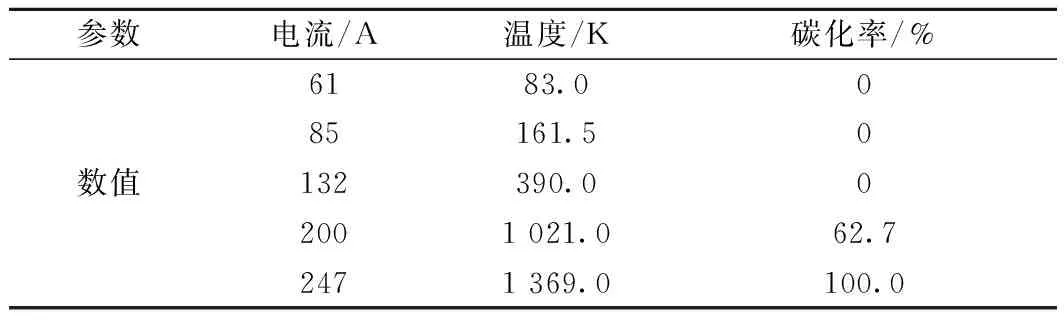
表6 不同电弧作用下绝缘节的碳化率
4 结论
(1) 在微观上,轮轨接触斑点是离散的,且轮轨泄放电流流经轮轨接触斑点时,电流密度基本呈现同心圆分布,且接触斑点中心处电流密度最大,这是由于中心处发生真实接触的接触面积最大,所以流经该单元的电流最多。
(2) 牵引电流通过轮轨接触泄放到钢轨上的电流越大,在轮轨接触斑点中心处产生的电弧电压也越大,电弧高温区域越大,对处于相同位置的绝缘节传热也越多,绝缘节发生碳化的几率、程度也越高。
(3) 由于正常工作时高铁站内单一车轮泄放在钢轨上的电流基本在100A左右,产生的电弧等级并不高,所以绝缘节的碳化率较小,200A电流所产生的电弧电压为74.4V,该电压下的电弧在绝缘节处的温度为1021K,造成绝缘节62.7%的碳化率,证明绝缘节烧损故障是由于低等级电弧多次作用造成的。
