周期模式下高速铁路车站到发线运用优化模型研究
2022-09-15单奕嘉乐逸祥徐瑞华王鹏玲
单奕嘉,聂 磊,乐逸祥,徐瑞华,王鹏玲
(1.北京交通大学 交通运输学院, 北京 100044;2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)
西欧、日本等地区和国家高速铁路(以下简称“高铁”)广泛采用周期化列车运行图,相应车站作业亦有周期化的特点。近年来国内学者更加关注“列车周期化开行”运输组织模式,并以京沪高铁、沪宁城际等线路为对象,研究更适应我国特点的周期化列车开行方案与周期化列车运行图编制方法,但针对周期模式下车站到发线运用的优化研究较少。
国外学者对咽喉区、到发线的研究起步于20世纪70年代,在研究初期,学者们往往将该问题简化为在固定前序列车作业顺序的基础上对单列车安排进路的多个子问题,并通常采用启发式算法求解[1];后发展为两者的综合优化,以及列车晚点下的动态调整,设计了线性化方法和精确求解算法[2-5];目前,国外许多国家对周期化列车开行模式的研究已较为成熟,如德国柏林中央客运站[6]、海牙HS站,通常采用周期事件规划问题(Periodic Event Scheduling Problem, PESP)构建周期化方案[4]。
国内学者在研究初期将咽喉区进路选择和到发线运用分开考虑[7-10];然后把咽喉区和到发线统一看作车站资源整体优化[11-12];最后提出到发线运用方案和运行图同步调整的方法[13]。
综上,考虑我国高铁车站设备特点和多样化、层次化出行需求的周期化车站到发线运用方案编制的研究非常少。本文结合国外车站到发线周期化运用的经验,以我国周期化列车运行图的特点和编制办法为基础,提出到发线周期化运用的编制流程,并建立多目标优化模型。
1 周期模式下车站到发线运用分析
到发线周期化方案的编制可参考周期图的编制方法。首先编制单周期车站到发线方案,保证按图行车时列车的接、发车作业不冲突,得到单周期方案;在此基础上,经过抽线调整,即把在其他周期内不开行的列车运行线剔除,拼接形成日周期方案。最后根据实际需要,插入非周期列车,加线调整得到全日方案,编制流程见图1。
周期化运行图是到发线周期化运用的基础,但并不意味着运行图实现周期化后即可形成到发线周期化运用方案,在方案编制过程中,需要在列车到发时刻周期化约束下,考虑:①相同到发时刻的同类列车在不同周期中应占用相同股道,即周期占用约束;②因同类列车在不同周期中占用相同的股道,除接发车进路不冲突外,还要满足动车组交路接续对到发线占用的要求,即把动车组出入段进路纳入考量;③为提高旅客换乘的便捷性,有中转接续关系的列车尽可能股道相邻或相近;④当车站衔接多个方向时,增加不同方向列车在车站的周期化接续约束;⑤在编制到发线运用方案时会出现部分列车的到发时刻不在同一个周期内,针对这类“过表列车”,需要确定合理有效的冲突疏解办法确保周期拓展后无冲突;⑥若采用“周期+非周期运行图”,在以高峰周期为基本单元构建的到发线运用方案可行的前提下,还需在其他周期出现非周期列车时保证非周期列车占用到发线的需求。
由于“周期+非周期运行图”下到发线运用比“非周期运行图”下到发线运用增加更多的到发线周期占用、中转接续约束等,求解更为困难。在列车密度比较大时,周期占用导致两列车间空挡时间增加,容易导致到发线能力不足而无解,鉴于此,提出以下3个关键问题。
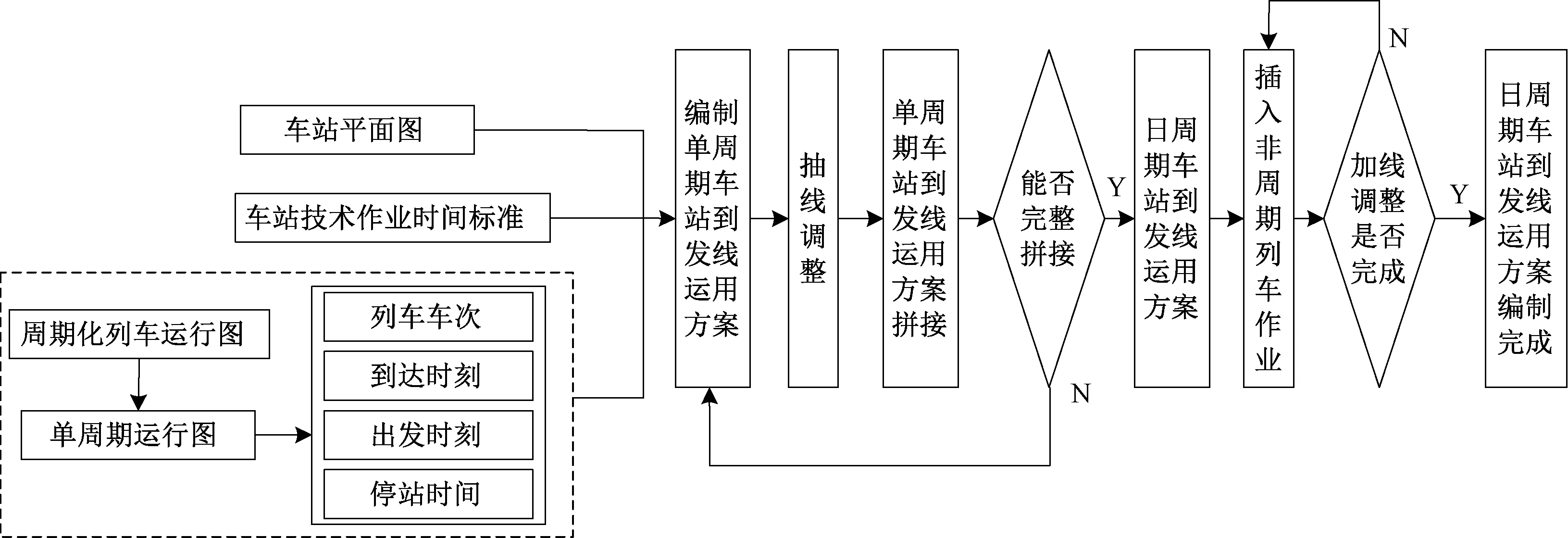
图1 周期化车站到发线运用方案编制流程
1.1 列车接续
周期化列车运行图在编图时有严格的频率约束和接续约束以方便旅客的出行和换乘[14]。文献[15]规定了最小列车接续时间(平均旅客换乘时间)h-和最大列车接续时间(平均旅客换乘时间加最大旅客等待时间)h+。
车站列车接续示意见图2,列车i的OD为A—D,列车i+1的OD为B—D,旅客从A站出发前往D站,只能在E站换乘。当这类旅客的人数较多时,编图人员会在编制周期图时将列车i和列车i+1设为接续关系,使这两列车的到发时刻尽量邻近。
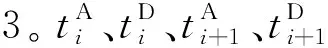
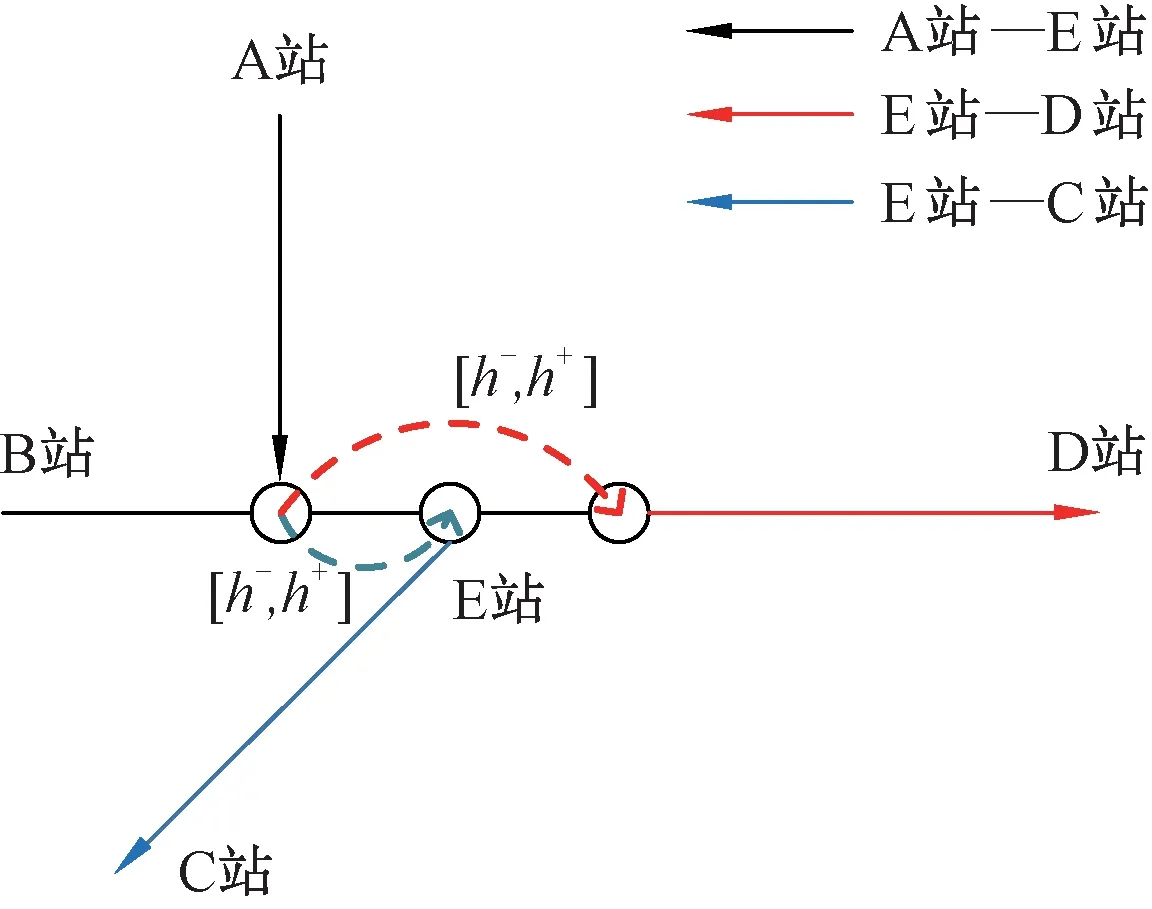
图2 车站列车接续示意图
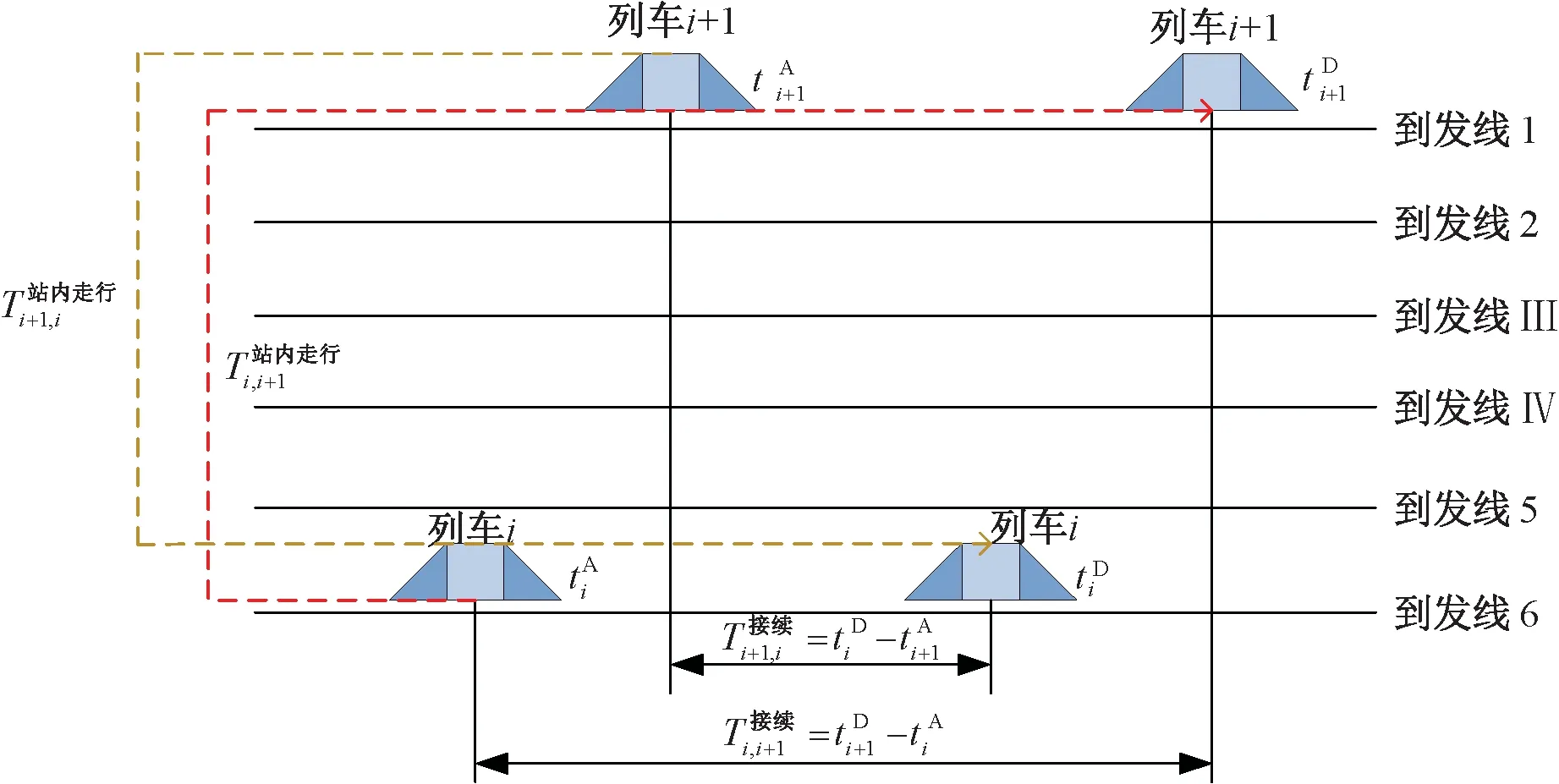
图3 到发线列车接续示意
若有旅客从列车i换乘至列车i+1,则必需满足换乘所需时间小于列车接续时间,即
(1)
反之,从列车i+1换乘至列车i,需满足
(2)
1.2 过表列车冲突消解与虚实时间窗
我国编图时,一般安排1 d(24 h)内运行的列车,而周期化列车运行图的周期一般为1 h或2 h,周期的缩短必然导致“过表列车”增加,即运行线跨多个周期的列车。
在编制车站到发线运用方案时,如果不考虑“过表列车”涉及的周期与研究周期的相互影响,在编完单周期方案拓展后很可能发生列车冲突,见图4,其中G1、G2等为车次。该方案中单个周期内的列车并无冲突,但由于未考虑“过表列车”G5和列车G1之间的关系,导致方案拓展后G5与G1发生冲突。

图4 过表列车冲突示意图
对于给定的运行图均有
(3)
式中:T为周期长度。
(4)
(5)
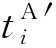
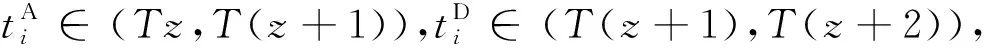
(6)
(7)

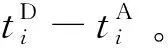
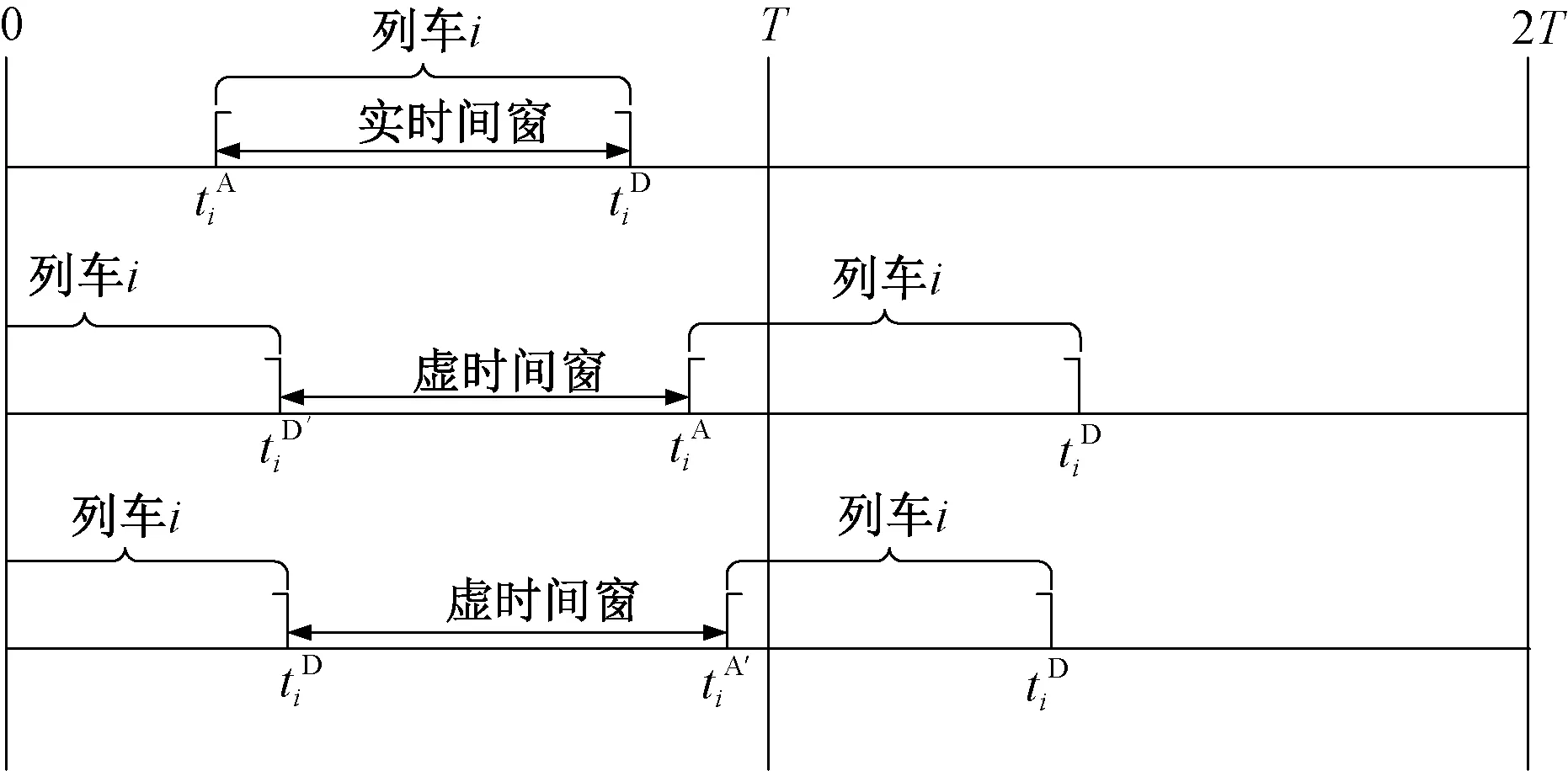
图5 实时间窗和虚时间窗示意
由于采用周期化列车运行图,研究周期内过表列车的到发时刻和邻接周期同一列(指列车类型、运行区间、运行速度等均相同)过表列车的到发时刻相同,因此可将两列车视为一列车处理。
1.3 非周期列车到发线安排
我国高铁具有“点多、线长、面广、跨线列车多”的特点,“周期+非周期”模式的运行图更适合我国国情[16],即首先编制高峰周期列车运行图,对个别周期抽线后拼接形成日周期运行图,然后以此为基础,在全图范围内添加非周期运行线。
在周期模式到发线运用方案中加入非周期列车需要考虑的因素比较多,目标函数与周期模式到发线运用方案也有不同,本文暂不考虑非周期列车的到发线安排。
2 周期模式下车站到发线运用优化模型
根据第1节分析,周期模式下车站到发线运用优化是在已知周期化列车运行图、车场平面布置图、车站作业分工、时间标准的情况下,满足方向性、到发线独占性、正线通过、抽线停运列车、旅客换乘走行时间与列车接续时间等约束的优化问题。由于要满足方案周期化要求,为保证在一个周期内能开更多的车,优化后的到发线运用方案应使列车的站内总走行时间最小;此外,考虑站内设备合理使用,将到发线均衡使用纳入优化目标。
2.1 符号说明
符号说明见表1。

表1 基础数据
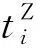
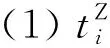
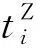
( 8 )

(2)δiejk计算方法
高铁车站安排到发线方案时,需统筹考虑列车接发车、出入段进路,使走行时间存在重叠的列车避开敌对进路,即进路冲突需同时满足两个条件:①列车在进路走行时间上存在交叉;②两条进路存在交叉。因此本文从时间维和空间维进行分析。
时间维上来看,接发列车时涉及接车走行时间、发车走行时间和站内作业时间,可能出现的冲突类型有3种,见图6。
接车(出段)与接车(出段)走行时间重叠列车集合为
( 9 )
发车(入段)与发车(入段)走行时间重叠列车集合为
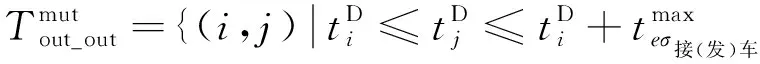
i,j∈Tmut}
(10)
接车(出段)与发车(入段)走行时间重叠列车集合为
i,j∈Tmut}
(11)

图6 咽喉区进路时间冲突类型
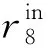
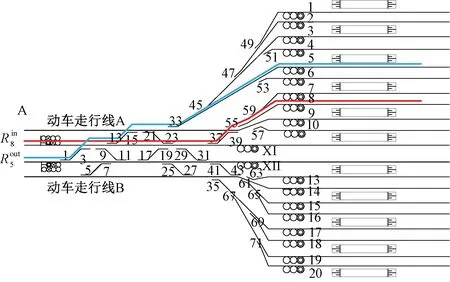
图7 咽喉区进路空间冲突类型
接车(出段)与接车(出段)敌对进路集合为
(12)
发车(入段)与发车(入段)敌对进路集合为
(13)
接车(出段)与发车(入段)敌对进路集合
(14)
因此,将走行时间存在重叠的列车集合与敌对进路集合作笛卡尔乘积,得到
Rin_outi,j∈Tmute,k∈Ladt}
(15)
2.2 目标函数
(1)列车站内总走行时间最小
接车走行范围从进站信号机起至各到发线动车组停车位置止。为使后行列车具备良好接车条件,前行列车必须尽快出清进路中的轨道电路区段。尽端式枢纽站折返列车较多,无论采用正接反发还是反接正发的形式,都必须跨越正线,与其余列车的接发车进路发生交叉。因此,为保证安全和提高车站作业效率,必须尽可能缩短列车进路走行时间,即该目标要求在无冲突的情况下选择距正线最近的到发线接发列车。
列车在站内的作业可分为3个环节:①接车(出段)作业;②列车停靠在到发线上进行的图定作业;③发车(入段)作业。在列车到发时刻确定的情况下,环节②时间固定,环节①与环节③的时间与列车占用的到发线有关,因此考虑优化环节①和环节③,即列车站内总走行时间Z1。
(16)
(2)到发线使用最均衡
到发线的利用率可用列车占用到发线的时间体现,用方差描述,即每一条到发线e的占用时间与到发线平均占用时间的偏离程度Z2。
(17)
2.3 约束条件
(1)到发线可达性约束。任意的列车i都受方向性的约束,即只能驶入可达的到发线进行作业。
(18)
(2)到发线独占性约束。作业过程中,任意的列车i只能选择一条到发线。
(19)
(3)正线通过约束。不停站通过列车必须由正线通过车站。
(20)
(4)占用同一条到发线会产生冲突的列车,即属于冲突列车集合Sij的列车i和列车j,不能安排在同一条到发线上。
xie+xje≤1 ∀(i,j)∈Sij∀e∈Ladt
(21)
(5)走行时间有重叠部分的列车不能选择敌对进路,即属于δ(i,e,j,k)的列车i,j,不能选择到发线e,k。
xie+xjk≤1 ∀(i,e,j,k)∈δiejk
(22)
(6)上水、吸污约束。需要办理上水、吸污作业的列车必需安排在具备办理该作业条件的到发线上。
(23)
(7)在高峰周期内存在其他周期抽线停运的列车,为保证到发线的均衡使用,在其他周期会抽线停运的列车需与正常运营列车安排在同一到发线上。
∀e∈Ladt∀i∈Tmut
(24)
(8)列车接续约束。若列车i,j存在接续关系,则两列车停靠到发线e、k之间的旅客换乘走行时间需小于两列车的接续时间。
xie+xjk≤1 ∀(i,e,j,k)∈φiejk
(25)
综上,式(16)~式(25)构成周期模式下到发线运用优化多目标模型;式(16)、式(18)~式(25)构成线性整数规划P1;式(17)、式(18)~式(25)构成非线性整数规划P2。
3 模型及算法分析
3.1 模型最优值分析
模型P1为纯整数线性规划问题,可得到全局最优解。
模型P2为二阶可微非线性函数,对决策变量xie求二阶偏导数,得到Hesse矩阵
(26)
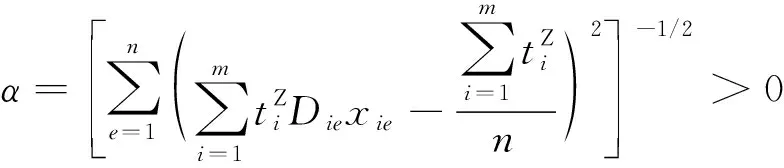
因Aee的顺序主子式
综上,P1、P2均可求得全局最优解。
3.2 基于Min-max Normalization的无量纲处理
目标函数式(19)指列车站内的总走行时间,量纲为时间;目标函数式(20)是到发线e占用时间和到发线平均占用时间的偏离程度,无量纲。采用Min-max Normalization(Min-max归一化)进行无量纲处理。
通常地,Min-max 归一化需分别单目标的极大值和极小值,即minZ1、maxZ1、minZ2、maxZ2,之后将x映射至(0,1)区间,得到
(27)
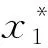
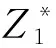
因此,
3.3 线性加权法
由最优值分析可知,P1、P2均可求得全局最优解,因此采用线性加权法,设置权重w1和w2,得到转化后的模型为
(28)
(29)
(30)
(31)
xie+xje≤1 ∀(i,j)∈Sij∀e∈Ladt
(32)
xie+xjk≤1 ∀(i,e,j,k)∈δiejk
(33)
(34)
(35)
∀e∈Ladt∀i∈Tmut
xie+xjk≤1 ∀(i,e,j,k)∈φiejk
(36)
算法流程见图8。

图8 算法流程
4 算例验证
选取北京南站京沪高速场(尽端式车站)、济南西站(通过车站)为例,采用京沪高铁周期化列车运行图设计方案,以验证模型、算法的有效性。
4.1 北京南站京沪高速场
北京南站京沪高速场共设12条到发线,其中14道、13道为京沪高速铁路正线,其余为到发线,所有股道均能办理旅客乘降作业。站场图见图9。
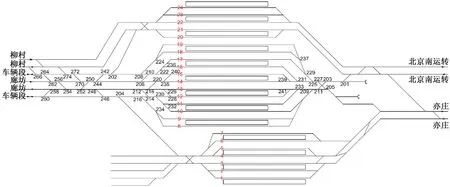
图9 北京南站站场图


表2 北京南站京沪高速场各到发线走行时间
由于无实际运营的周期化列车运行图,采用以1 h为周期,单周期开行11对列车的理论周期化列车运行图做案例研究。北京南站京沪高速场1 h周期化列车时刻表见表3。

表3 北京南站京沪高速场1 h周期化列车时刻表
(1)所有车底均按立折列车处理

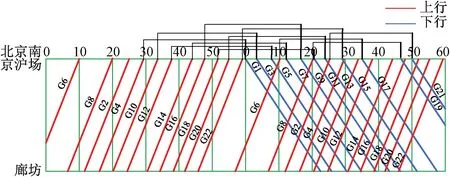
图10 车底交路
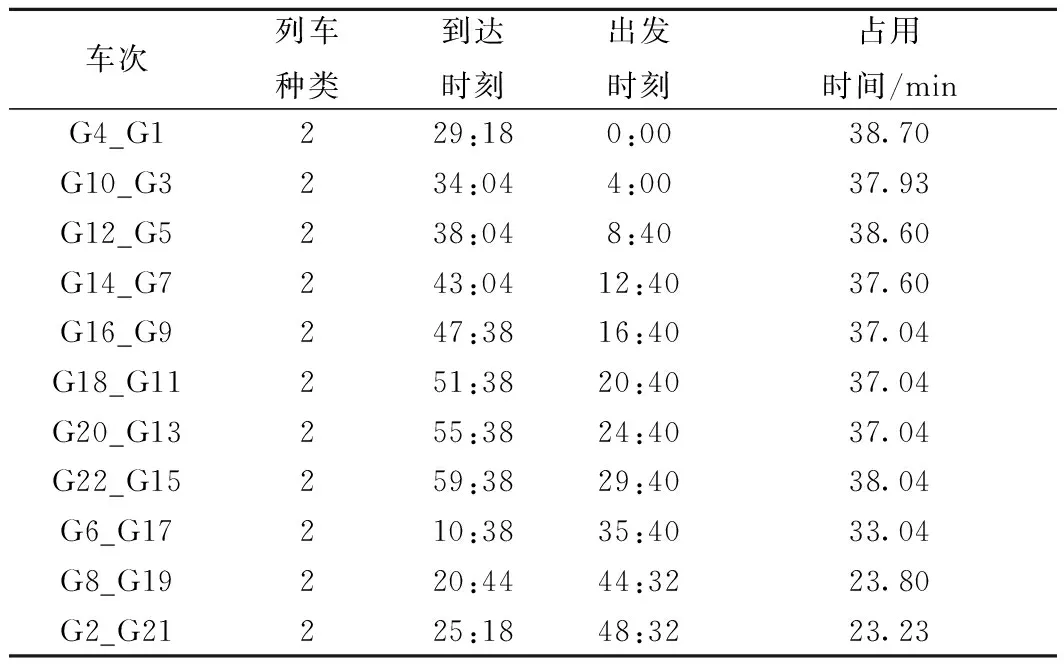
表4 北京南站京沪高速场列车到发时刻表Ⅰ
然而,实际运营中,北京南站京沪高速场的现有能力最多安排11列立折列车,且这些列车在到发线上的作业时间均为20 min,见图11。

图11 北京南站京沪高速场到发线运用方案
表4中11列立折列车在到发线上的作业时间超过30 min。将数据代入求解软件为无解。可见,京沪高速场的能力不足以安排作业时间超过20 min的11列立折列车,因此,将其中部分立折列车改为始发、终到列车,并进行出入段处理。
(2)部分车底立折,部分车底出入段
因无法将时刻表中的11列立折列车全部安排完,所以进行小规模的遍历,采用Matlab R2018b进行数据处理,利用Yalmip工具包调用Cplex求解,发现最多可安排8列立折列车。在此基础上将其余3列立折列车分解得到6列始发终到列车,在到发时刻固定且到发线作业时间为15 min的前提下,始发列车看作于出发时刻前15 min从车辆段到达的立折列车,终到列车看作于到达时刻后15 min发往车辆段的立折列车。
以上述思路优化得到最终结果见表5和图12。由于站场能力限制,6列始发或终到列车仍然只能安排其中的2列终到列车(G6,G8)和1列始发列车(G17),见表5。
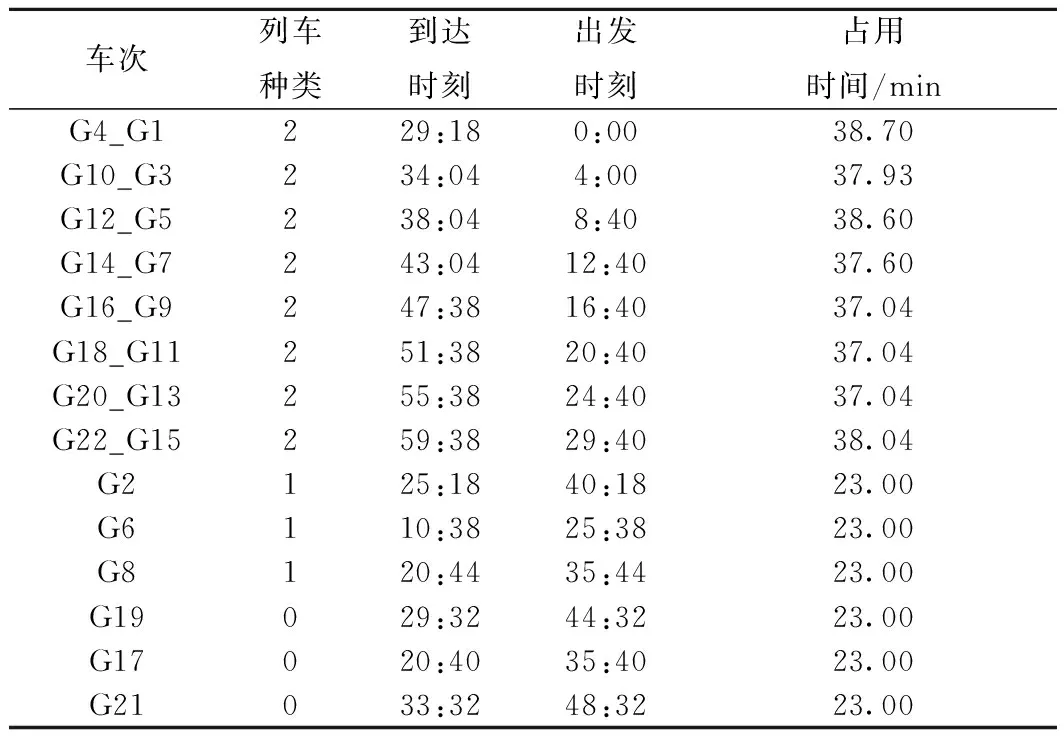
表5 北京南站京沪高速场列车到发时刻表Ⅱ

图14 北京南站京沪高速场到发线运用方案拼接

图12 北京南站京沪高速场部分车底立折、部分车底出入段方案
后续可考虑将到发线作业时间定义为决策变量进行求解,而非固定成15 min;或是反馈回时刻表编制系统[18],通过反馈调整列车时刻表和动车交路以减少对到发线的占用时间等来解决部分列车无法安排的问题。
在该算例中,模型P1和P2所得结果相同,见图12,且两方案的指标一致,即列车站内总走行时间均为79.7 min,方差均为38.99,因此该方案为最优解,不再做协同优化处理。
本文整理由程序得出的走行时间存在重叠的冲突列车集合,验证集合的正确性和完整性后将求解方案映射至站场图中,见图13。手工校验后,求解方案有效。
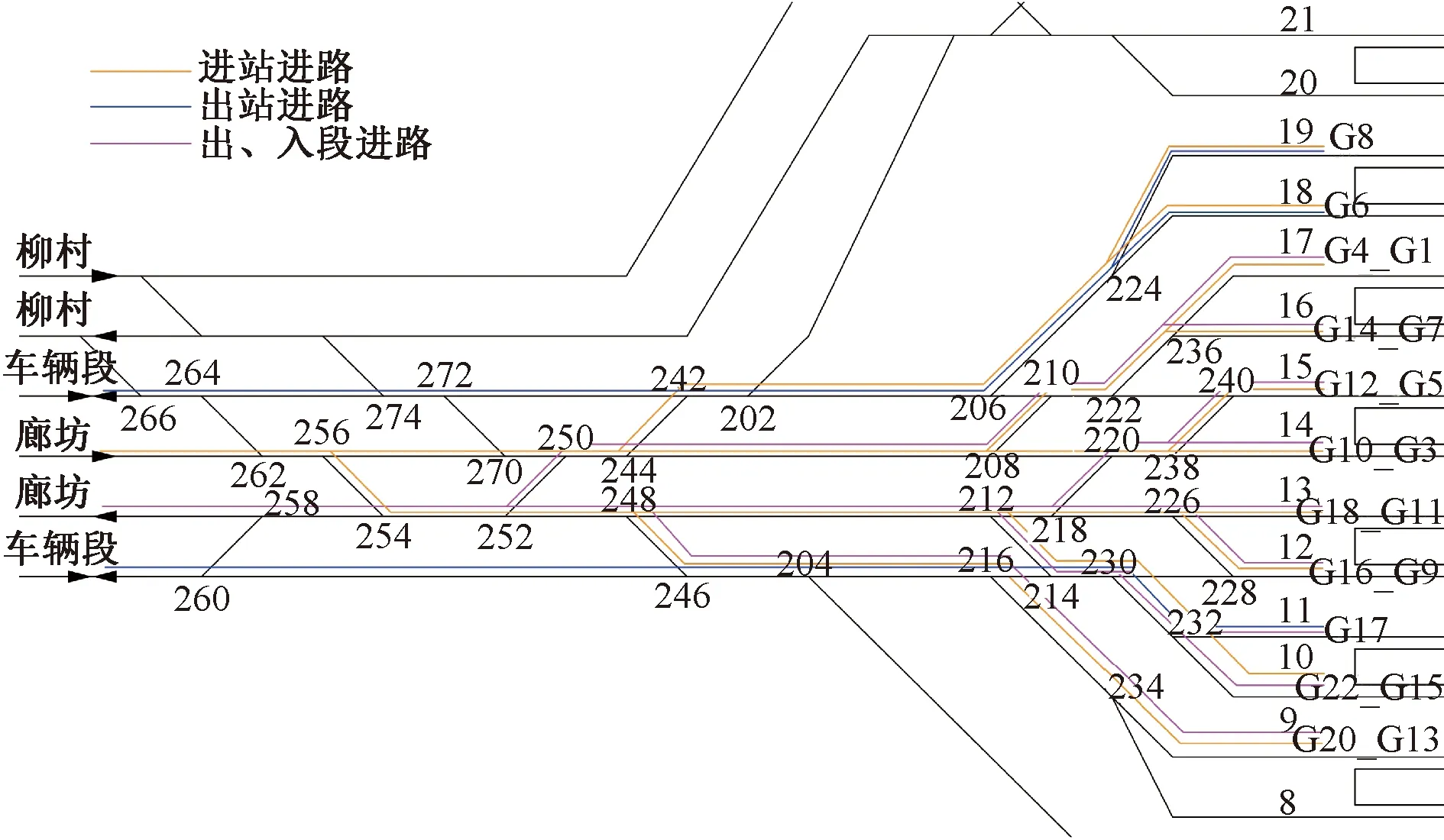
图13 北京南站京沪高速场到发线运用方案(站场)
以图12所示单周期方案进行拼接,结果见图14,拼接后的方案未发生冲突,过表列车冲突成功消解。
求解方案单周期接发了8列立折列车、2列终到列车、1列始发列车。与理论上京沪高速场1 h内最多安排11列以20 min为标准进行作业的立折列车数量接近。但是在求解得到的方案中,列车对到发线的平均占用时间为33.73 min,而以20 min为标准进行作业的立折列车对到发线的占用时间为28 min,求解方案对到发线的总利用率更高。
η为到发线能力利用率即单周期内,各到发线被占用的时间与周期长度T的比值,其计算式为
(37)
求解方案与11列立折列车理论方案相比,各到发线的能力利用率总体更高,见表6。
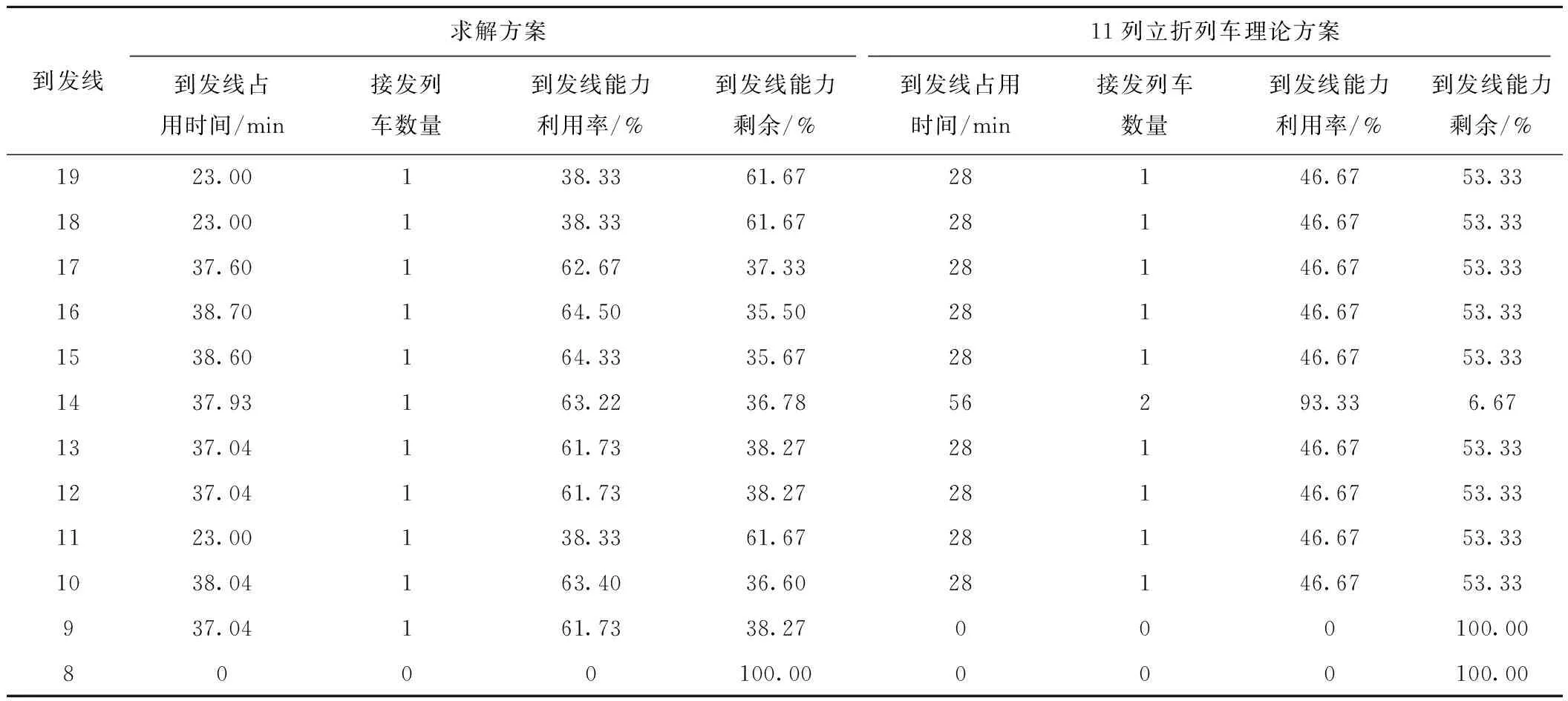
表6 北京南站京沪高速场到发线能力利用率
4.2 济南西站
由于北京南站为尽端式车站,以始发终到列车为主,显示周期模式下能力紧张。进一步选取以通过列车为主的济南西站进行分析,其站场图见图15。仍采用同一周期图化列车运行图,表7中列车种类4为通过列车。
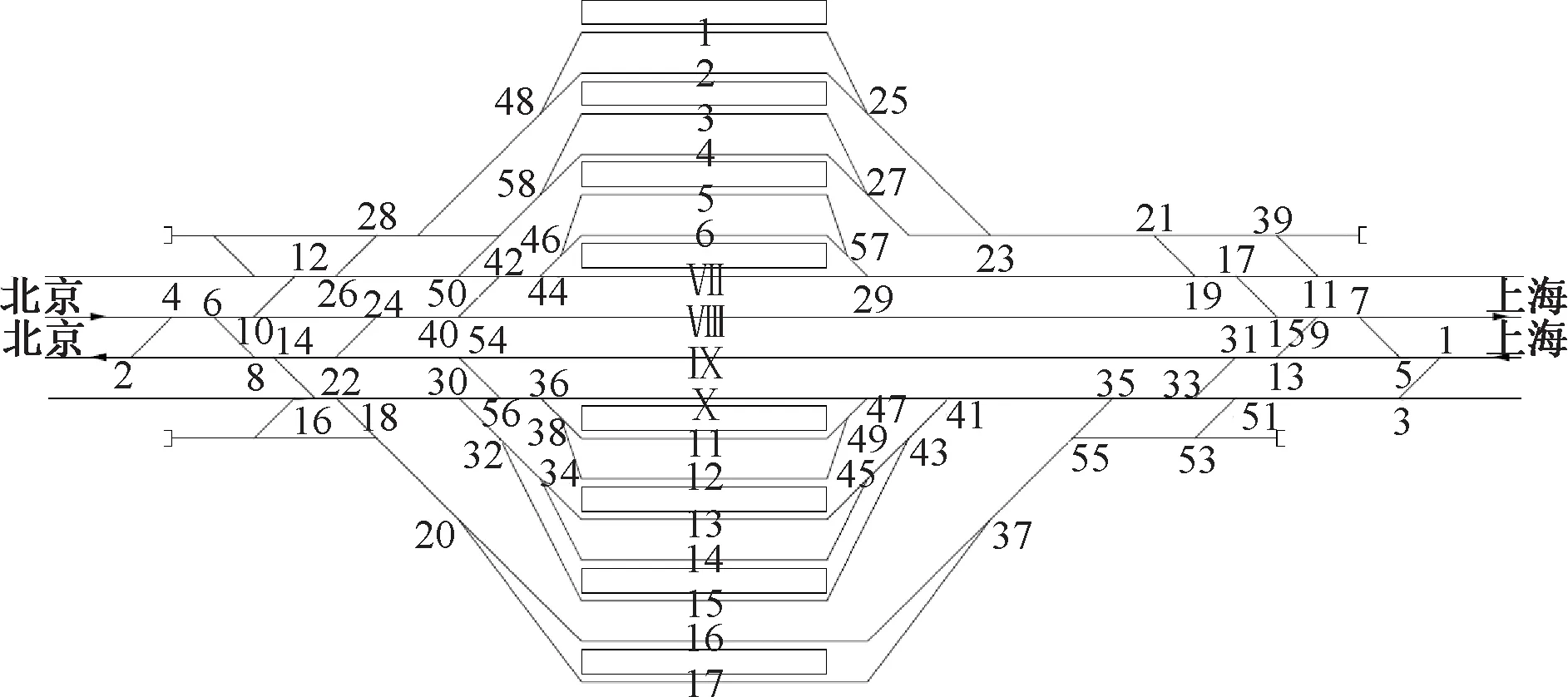
图15 济南西站站场图
求解方案单周期共接发了22列车,其中21列停站通过列车,1列不停站通过列车。以Z1和Z2的数值作为评判指标,将模型P1、模型P2方案、协同优化方案进行比较。
该案例中,模型P1和P2所得方案不同,分别为图16(a)和图16(b)。将ω1和ω2取值0.5,即总走行时间和到发线均衡使用同等重要,使到发线运用方案在Z1最小和Z2最小之间协同,得到如图16(c)方案,求解方案符合有效性和周期化运用要求。

表7 济南西站1 h周期化列车时刻表
如图17,模型P1方案的Z1为101.4 min,Z2为65.77;模型P2方案的Z1为112.4 min,Z2为13.83;协同优化方案是对两者的协同优化,指标Z1与Z2介于两者之间,分别是107.6 min和30.36。

图16 济南西站到发线运用方案

图17 济南西站目标函数值分析
4.3 不同站型下到发线运用方案对比
(1)到发线使用方案对比
北京南京沪高速场方案中无上下行车场区分,但因为始发、终到列车有出、入段作业,因此,终到列车G6、G8在18、19股道作业;始发列车G17在11股道作业。
济南西站方案中有上下行车场区分,11列下行列车中有10列安排在车场1~6股道,为使到发线运用均衡将1列安排在12股道;11列上行列车中有10列安排在11~17股道,1列不停站列车由正线IX通过。
(2)咽喉区占用时间对比
咽喉区占用时间对比见表8,经计算,北京南站京沪高速场以1 h为周期的方案中对咽喉的总占用时间达到了79.7 min,其中11.8 min为出入段占用咽喉区的时间,67.9 min为接发列车占用咽喉区的时间;济南西站以1 h为周期的方案中无出入段,对两端咽喉区总占用时间均为53.8 min。
由于追踪间隔时间大于列车站内的最大走行时间,所以接发车时并不会发生冲突;此外,济南西站无出入段作业,因此接车与接车、发车与发车以及出入段进路不纳入统计范围。两站咽喉区的敌对、平行进路数量见表9。
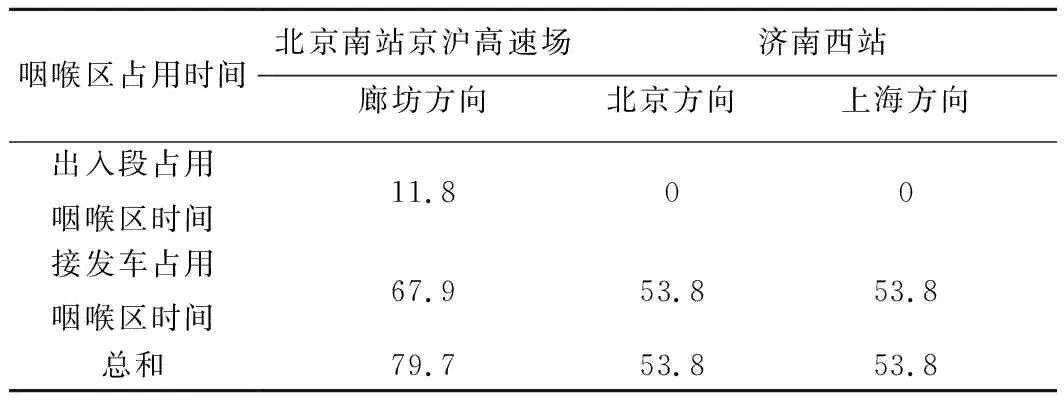
表8 咽喉区占用时间对比 min
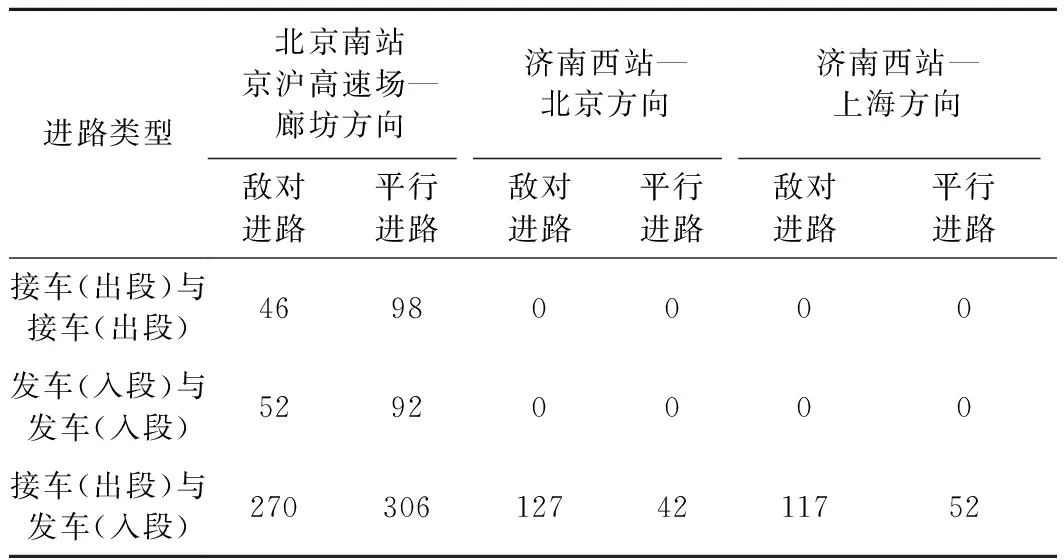
表9 咽喉区进路交叉干扰数量对比(仅京沪高铁方向) 条
算例中,济南西站到发线能力相对富裕,两站相比,主要原因有二:
(1)北京南站京沪高速场为尽端式车站,所有作业的进路均在一端咽喉区,且均是始发终到列车。做立折列车处理时,若列车接车时选择14~19股道,则其相应的发车进路就会切割整个咽喉区;若接车时选择8~13股道,虽缓解了发车时冲突多的问题,但其接车进路又横跨了咽喉区。此外,因为以1 h为周期,导致在周期内一条到发线基本只能安排一列立折列车。
若做始发终到列车出入段处理,则终到列车可接入14~19股道,入段后由8~13股道发车,消除了立折列车必定会切割咽喉区的痛点。且因为出入段进路与接发车进路交叉的比例较低,可在一定程度上增加平行进路的数量,如表9中北京南站京沪高速场接车(出段)与接车(出段)、发车(入段)与发车(入段)和接车(出段)与发车(入段)的平行进路数较多的情况,便是因为考虑了出入段的进路。从案例中也可以看出,当部分列车做始发终到处理时,成功安排了相对更多的列车。
济南西站为通过式车站,在本例中均为通过列车(包括停站通过和不停站通过),且接发车进路分布在车站的两端咽喉。因此通过济南西站的列车只需要按照上、下行场的分布进行作业即可消除接、发车的冲突。
(2)北京南站京沪高速场的咽喉区能力与到发线能力不匹配。由(1)分析可知,北京南站京沪高速场中的立折列车一定会切割一次咽喉区,若使列车出入段可避免这类问题,但也由此出现始发、终到列车的接发车平行进路较少的情况。
如图18(a)所示,若在8~13股道接车,列车必须且只能经由256-254-252-248去往到发线;然而,8~13股道的发车进路同样需要经由248-252-254,导致这些股道无法同时进行接车作业和发车作业,限制了到发线的能力。
如案例中无法安排的G19,其出发时刻为44:32。G16_G9的到达时刻为47:38,两者在走行时间上存在重叠部分。求解方案中,G16_G9的接车进路完全切割了8~13股道的接发车进路,因此即使股道8上没有列车,G19也无法停靠。但若是在满足车站设计条件的前提下增设如图18(b)内红线所示的道岔(300-302)即可疏解这类冲突,增加了8~13股道接车和发车的平行进路数量,从而提高咽喉区能力以进一步释放到发线利用率。
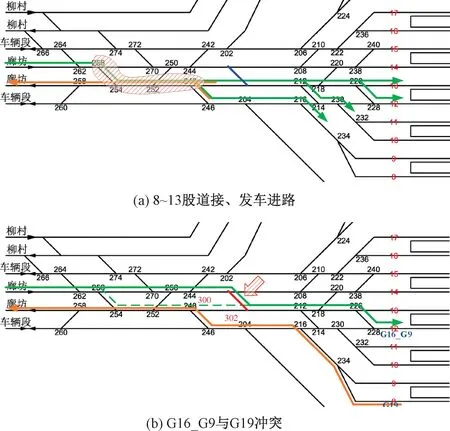
图18 北京南站京沪高速场咽喉区分析
5 结论
本文以周期化列车运行图的特点和编制办法为基础,提出到发线周期化运用的编制流程,并指出3个技术难点;以列车在站内总走行时间最小、到发线运用最均衡构建了周期模式下车站到发线运用多目标优化模型,利用Matlab、Cplex编程实现;以北京南京沪场和济南西分别作为尽端式车站、通过式车站的代表进行算例研究,分析表明论文模型有效,过表列车冲突成功消解,为到发线运用方案周期化提供理论方法,但从算例也可以看出以始发终到为主的车站,周期模式下如果立折列车较多,折返之间较长时,到发线能力紧张。
