从采样的角度谈信号与系统中的傅里叶变换

王 琳， 胡 耀， 王世元

(1.西南大学 电子信息工程学院，重庆 400715；2.非线性电路与智能信息处理重庆市重点实验室，重庆 400715；3.重庆工商职业学院，重庆 401520)

引言

《信号与系统》是电子信息大类专业本科生的一门专业核心课，通过该课程的学习能够帮助学生建立利用变换域分析处理信号的思想以及从系统的角度考虑分析问题的观念[1]。该课程以高等数学、工程数学、电路分析等课程为基础，其后续课程为数字信号处理、通信原理以及数字图像处理等[2]。因此，《信号与系统》在电子信息类本科生的培养环节中起到了承上启下的作用[3]。该门课程概念比较抽象、理论性强、内容又相对比较枯燥[4]。在学习过程中，部分学生感觉比较吃力，主要体现在以下几方面：一是对一些重要理论理解不够深入，尤其是其实际和工程意义；二是该课程涉及大量计算，且部分计算的相似度较高，同学们在埋头计算的过程中，往往失去对部分概念的清晰把握；三是对个别知识点，单个的还掌握得比较到位，但对知识点之间的相互关系，常常缺乏深入理解、难以融会贯通。针对《信号与系统》教学过程中出现的上述问题，本文就该课程中“几种傅里叶变换之间的相互关系”这部分内容进行了教学探索。该内容既是《信号与系统》课程的重点又是难点，涉及的数学知识也比较多，知识点之间既有区别又有联系。学生在学习过程中往往感觉较难，到期末复习甚至考研阶段还有不少同学捋不清几种傅里叶变换之间的相互关系；同时，也常看到有人在知网、百度等论坛上咨询这个问题。希望通过笔者的探索，帮助大家轻松理解几种傅里叶变换之间的相互关系。

古诗云：“横看成岭侧成峰，远近高低各不同”。对同一个事物，从不同的角度去分析、理解，会有不同的想法和收获。本文从采样定理出发、结合时域和频域的特点来理解傅里叶的各种变换。结构安排如下：首先，对几种傅里叶变换进行简要回顾，接着分析几种傅里叶变换在时域和频域的特点；最后，采用思维导图的勾勒来对知识点及其相互关系进行描绘，梳理、总结几种傅里叶变换的相互关系。

1 几种傅里叶变换在时域和频域的特点

本部分内容涉及几种傅里叶变换以及采样定理，下面依次简要介绍。通过以往的学习可知，傅里叶变换是针对非周期信号或非周期序列进行的从时域到频域的变换，傅里叶级数是针对周期信号或周期序列进行的从时域到频域的变换。

1.1 连续时间傅里叶变换(Continuous Time Fourier Transform,CTFT)

以门函数为例，来分析连续时间傅里叶变换在时域和频域的特征。如图1a、b所示，一个宽度为τ高度为1的门函数，它在时域是连续、非周期的；在频域也是连续、非周期的。

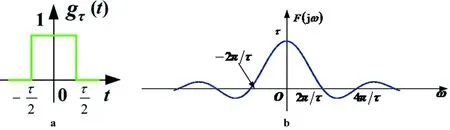
图1 连续时间傅里叶变换示例Fig.1 Example of continuous time Fourier transform

1.2 离散时间傅里叶变换(Discrete Time Fourier Transform,DTFT)

此处以方波序列为例。如图2a、b所示，一个从-2到2的方波序列，它在时域是离散、非周期的；在频域是连续、且以2π为周期的。

图2 离散时间傅里叶变换示例Fig.2 Example of discrete time Fourier transform

1.3 连续傅立叶级数(Continuous Fourier Series,CFS)

根据前面的讲述可知：CFS针对的是在时域连续的周期信号。CFS有三角和指数两种形式。例如，画出图3a所示周期矩形脉冲f(t)的频谱Fn，此处，令T=4τ。经求解可得图3b，从图上可以看到，CFS在时域是连续、周期的；在频域是离散、非周期的。

图3 连续傅立叶级数示例Fig.3 Example of continuous Fourier series

1.4 离散傅立叶级数(Discrete Fourier Series,DFS)

DFS针对的是在时域离散的周期序列。如图4a所示，为一个以N为周期、在-M到M幅值为1的DFS，令N=30、M=2把它展开成傅里叶级数，如图4b所示，在频域它仍然是离散、周期的。

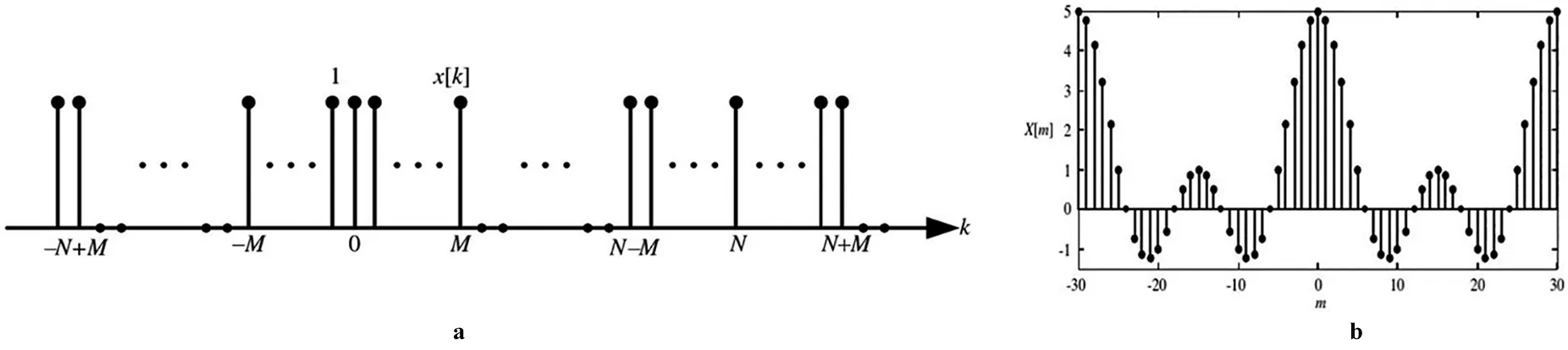
图4 离散傅立叶级数示例Fig.4 Example of discrete Fourier series

在完成了以上四种傅里叶变换的教学后，很多同学反映已经感觉比较迷糊。通常在这一阶段需要给同学们留一点时间自行回顾一下，并在随后的教学中加入对上述四种傅里叶变换的梳理工作。这里，需要重点理清傅里叶级数和傅里叶变换的关系。傅里叶级数是由法国数学家让·巴普蒂斯·约瑟夫·傅里叶提出的。傅里叶级数的出现极大地推动了偏微分方程的发展，解决了关于弦振动问题解的争论，促进了函数概念的进一步发展和完善。傅里叶级数分为连续时间傅里叶级数和离散时间傅里叶级数，分别针对的是连续周期信号和离散周期信号。傅里叶级数有指数和三角两种形式。连续时间傅里叶级数针对连续信号进行计算，任何连续周期信号都可以展开为正弦信号和余弦信号构成的无穷级数。三角函数利用欧拉公式可以转化为指数形式，指数形式的连续时间傅里叶级数中的负频率并没有实际物理意义，引入负频率仅仅是为了便于计算。

傅里叶级数研究的是周期信号，在一定条件下，非周期信号可以理解为一种特殊的周期信号。对一个周期信号而言，如果其周期足够大，可将其作为非周期信号来理解。简单地说，通过将周期信号的周期拓展到无穷大，则非周期信号就可以理解为一种特殊的周期信号。当信号的周期趋于无穷大时，傅里叶级数即为傅里叶变换。傅里叶变换实现了信号的时域和频域之间的对应关系，在数学、物理学、通信、金融等领域都有着非常广泛的应用。

1.5 离散傅里叶变换(Discrete Fourier Transform,DFT)

CTFT、DTFT、CFS、DFS这四种傅里叶变换已经包含了连续的、离散的、周期的、非周期的信号和序列，为什么还要进行离散傅里叶变换呢？这是为了便于利用计算机来进行傅里叶变换而规定的一种专门运算。DFT不是对任意信号都可以进行，只能对有限长序列才可以。这里，仍然以方波序列为例来分析。如图5a所示，将有限长序列f(k)以N=10为周期延拓成周期序列fN(k)，变换得DFS，再对DFS取主值即可得DFT，如图5b。从这个例子可以看到，DFT在时域和频域都离散且序列长度有限，这个特点就是为什么计算机实现的时候要采用DFT的原因。

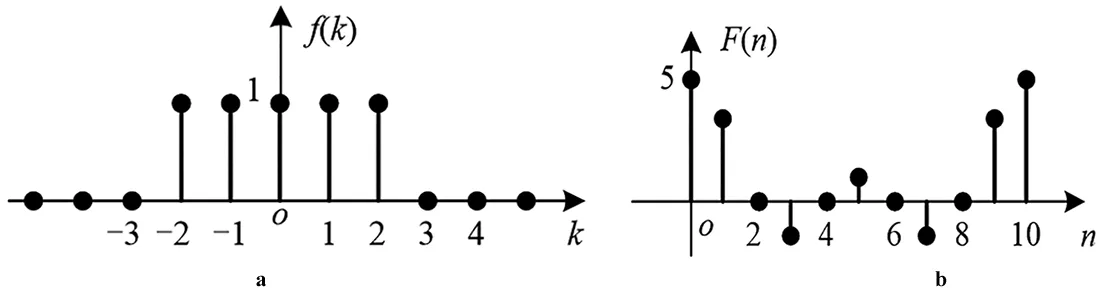
图5 离散傅立叶变换示例Fig.5 Example of discrete Fourier transform

对于离散序列，其DFT的快速算法称之为快速傅里叶变换(Fast Fourier Transform,FFT)。由于DFT采用矩阵相乘，算法复杂度为信号规模的平方，而FFT有效利用了旋转因子的对称性，从而很好地降低了DFT的复杂度，提高了运算速度。

以上即为《信号与系统》课程中涉及到的六种傅里叶变换。在教学实践中，学生对“几种傅里叶变换”这部分内容学习起来感觉比较吃力，归纳起来，原因主要有以下几点：一是，教材中这部分内容对计算的推导比较详细，但对几种傅里叶变换的意义和实际应用介绍得比较欠缺。学生在学习过程中注意力被大量的推导和计算牵制，忽略了对傅里叶变换的物理意义及变换其目的的把握，容易出现知其然而不知其所以然的情况。二是，该部分内容涉及的几个傅里叶变换具有较高的相似度，在初步接触傅里叶变换的阶段，容易被大量相似而又有区别的计算和推导弄晕。很多同学反映，学习一种新的傅里叶变换的时候，需要对之前已经介绍过的傅里叶变换进行反复回顾，以比较其区别；并且极易在反复的比对中产生焦虑和烦躁情绪，影响对该部分知识的学习和掌握。三是，教材中对几种傅里叶变换的介绍比较详细，但是对几种傅里叶变换之间的关系介绍得比较粗略，且欠缺对该部分内容的整体梳理。笔者及其团队在教学实践过程中，密切关注教学效果、与学生进行多渠道沟通，获取来自学生的反馈，并结合自身教学经验，针对现有教材和教学方式存在的不足，基于采样定理结合傅里叶变换时域和频域特征，对六种傅里叶变换之间相互关系进行整体分析。通过分析和梳理，将几种傅里叶变换之间的关系进行了重新组织，以期学生在学习过程中能够更容易、更深入地理解和掌握该部分内容。下面，将对采样定理进行简要介绍。

采样定理又称取样定理(原理图见图6)，是通信与信号处理学科中一个重要的基本结论。该定理论述了在一定条件下，一个连续时间信号可以用该信号在等时间间隔上的样本值表示。“采样”就是利用采样脉冲序列从连续时间信号中“抽取”一系列离散样本值的过程。这些样本值包含了该连续时间信号的全部信息，当满足采样定理，还可以把离散信号恢复为原信号。采样的实质就是离散化(或数字化)。采样，架起了连续与离散时间信号之间的桥梁，为其相互转换提供了理论依据。

图6 采样定理原理图Fig.6 Schematic diagram of sampling theorem

在对几种傅里叶变换分析的基础上，以非周期信号为例进行说明。如图7所示，一个宽度为τ高度为1的门函数gτ(t)，在时域它是连续、非周期的。令τ=4，对其在时域进行采样，得到从-2到2的方波序列f(k)。分别对gτ(t)和f(k)进行CTFT和DTFT，得F(jω)和F(ejω)。可以看到：CTFT在时域和频域都是连续、非周期的，DTFT在时域是离散、非周期的，在频域是连续、周期的。对这个连续的周期信号F(ejω)在2π周期内，进行N=10次均匀采样。此时，是在频域进行采样，也就是在频域进行离散化处理，就得到了DFT。

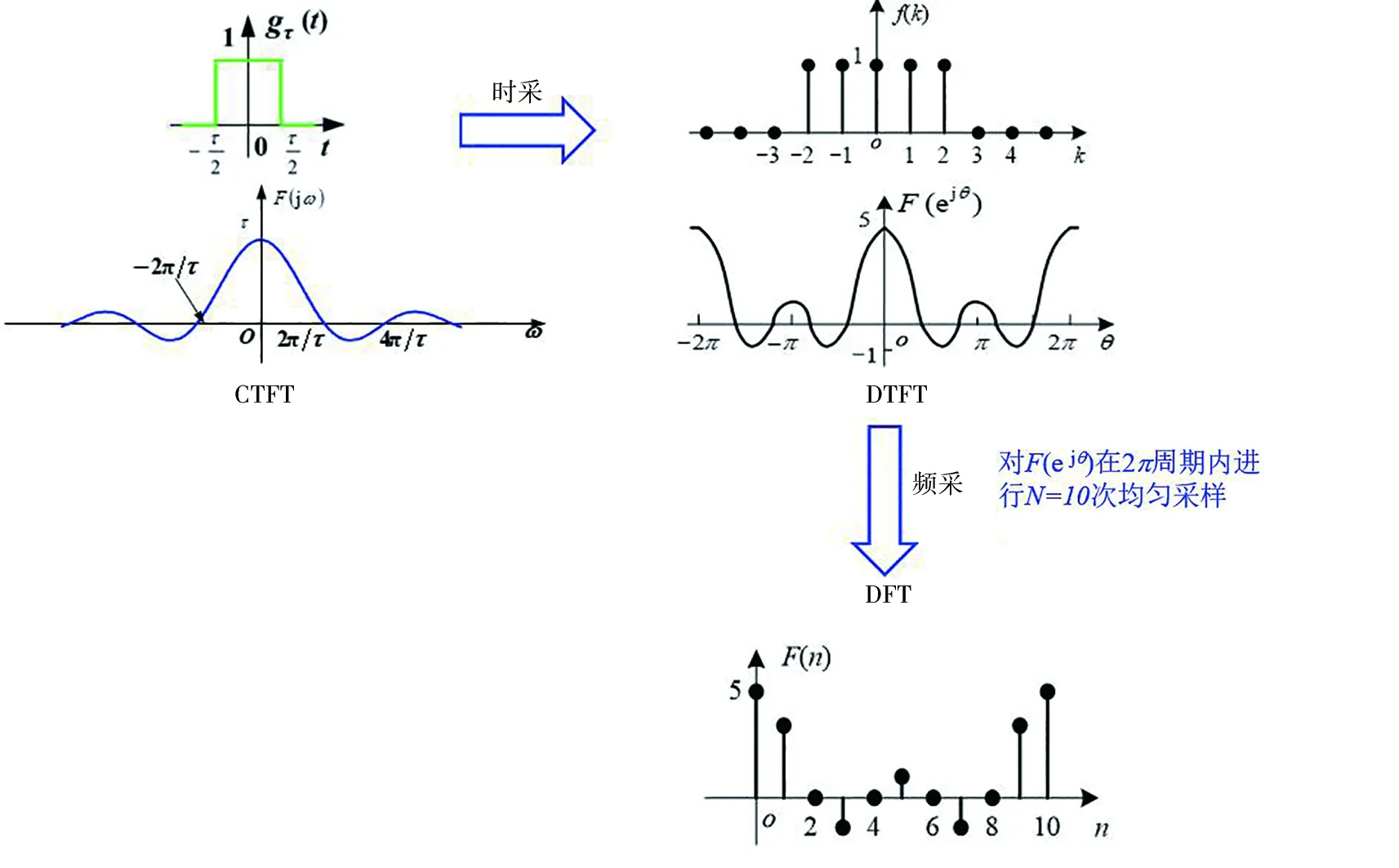
图7 基于采样定理数字化处理过程举例Fig.7 Example of digital processing based on sampling theorem

该例说明：时域的采样会产生频域的周期性延拓。基于傅里叶变换的对称性，同理，频域的采样也会产生时域的周期性延拓。即：一个域的离散会导致另一个域的周期性延拓。

2 思维导图

思维导图是一种图形思维工具，简单有效，能很好地表达发散性思维。思维导图利用图形和文字工具，把各级主题之间的关系用隶属和相关的层级图表现出来，便于记忆和理解。

要理解傅里叶的各种变换可以从采样定理出发，结合时域和频域的特点来进行。基于本文第2部分的分析，构筑思维导图如图8所示，几种傅里叶变换时域、频域特征如表1所示。针对非周期信号或序列的CTFT、DTFT，针对周期信号或序列的CFS、DFS。CTFT和DTFT在时域的区别就是一个连续、另外一个离散，所以，可以通过时域的采样来实现。类似地，CFS和DFS也可以通过时域的采样来关联。CTFT在时域和频域都是连续、非周期的，DTFT在时域是离散、非周期的，在频域是连续、周期的。CFS在时域是连续、周期的，在频域是离散、非周期的。DFS在时域和频域都是离散、周期的。根据傅里叶变换的对称性，由于频域的采样会导致时域的周期性延拓，所以，从CTFT到CFS以及从DTFT到DFS都可以通过频域的采样来实现。对DFS取主值得到DFT，对DFT进行快速运算就可以得到FFT。以上就是基于采样定理，结合傅里叶变换时域和频域特征，对六种傅里叶变换之间相互关系的分析。

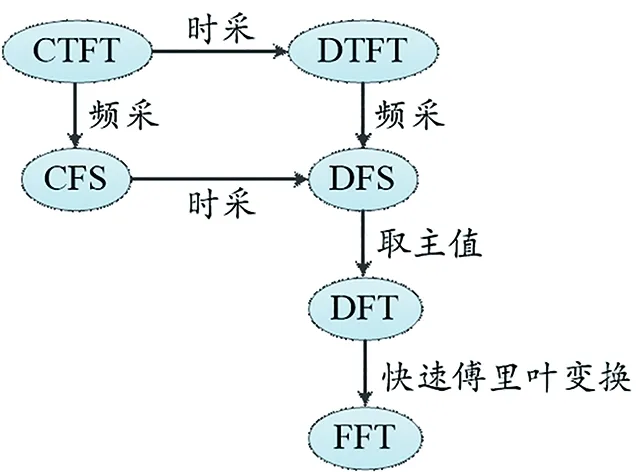
图8 从采样定理出发理解傅里叶的各种变换Fig.8 Understanding Fourier transforms by sampling theorem

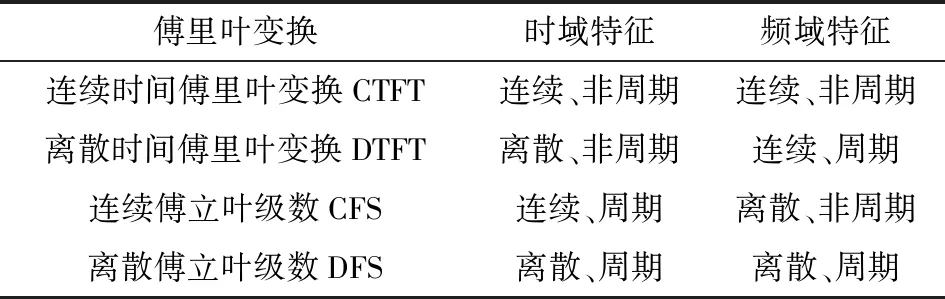
表1 几种傅里叶变换时频域特征对照Table 1 Comparison of time-frequency domain features of Fourier transforms

3 教学实践结果

在《信号与系统》课程较长时期的教学过程中，笔者及团队深深体会到教好这门课程是很不容易的。该课程知识点多、信息量大，涉及大量的计算，就需要学生在理解的基础上清晰掌握各个重要知识点，熟练推导过程，并能够进行精确计算。在该课程的教学过程中，一方面，需要教师胸有成竹且讲授合理；另一方面，需要学生积极主动投入大量精力，且具有百折不挠的精神，从而克服学习过程中遇到的各种困难。对教师而言，合理引导并对重要知识进行梳理、总结以方便学生理解就显得尤为重要。怀着这个初衷，笔者及其所在教学团队就傅里叶变换这部分知识，通过构筑思维导图，以采样定理为主线，对《信号与系统》课程中的傅里叶变换时域和频域的关系进行了重新组织，并在实际教学过程中进行了实践。

教学实践主要分为两个阶段：第一阶段为教师引导教学阶段。在按照课本内容学习完几种傅里叶变换、学生对该部分内容有了初步认识以后，教师基于采样定理将六种傅里叶变换按照思维导图的逻辑顺序进行梳理讲解，利用时域和频域的采样将六种傅里叶变换进行关联。在这一阶段，教师应注意把握和控制学习的主动权，尽量对学生进行引导，使其充分理解并跟上教师的教学思路。经实践，讲授这部分内容大约需要十五分钟，通常应将这部分内容安排在一次课的收尾部分。第二阶段为学生自主学习阶段。根据笔者及其教学团队的实践，该阶段主要以布置一次课后作业的形式来完成。通过布置一次作业，引导学生在课后自主对知识点进行巩固和总结，并对思维导图进行浮现。这样，就能促进学生对知识点的充分理解和掌握，从而收到较好的学习效果。时间允许的情况下，可以在两个教学阶段完成以后，在后续课堂上，花两、三分钟，以提问的方式对学生的掌握情况进行评估，以更好地把握教学质量。

迄今为止，笔者已在西南大学为数届电子信息类本科生讲授了《信号与系统》课程，近三年该课程的教学信息如表二所示。在教学过程中，最初采用的教材是吴大正主编、高等教育出版社出版的《信号与线性系统分析》第四版[5]，后更新至第五版[6]；该教材是普通高等教育“十五”国家级规划教材，也是国内大部分高校信号与系统课程选用的经典教材。在课后作业方面，每学期通常会布置五至七次作业。在考试方面，每学期以闭卷统考形式分别安排一次其中和期末考试。

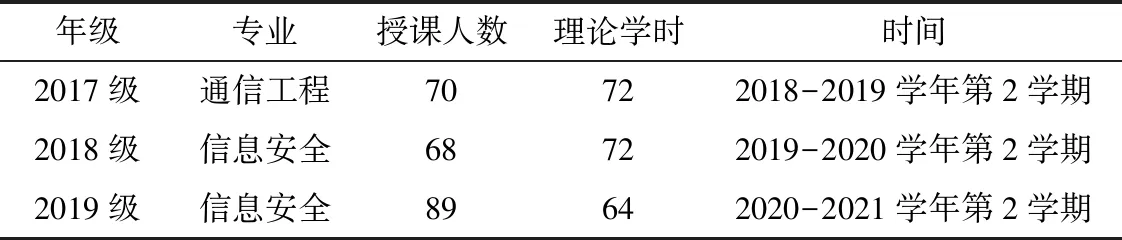
表2 《信号与系统》课程教学信息Table 2 Teaching information for the course Signals and Systems

按照教学进度安排，在将六种傅里叶变换和采样定理全部讲解以后，笔者基于采样定理，结合傅里叶变换时、频域的特征，对六种傅里叶变换之间的相互关系进行梳理和总结，学生普遍反映较好、课堂气氛活跃。有学生反映，基于该方法的梳理，对充分掌握、理解几种傅里叶变换有很大帮助。

《信号与系统》这门课程的期末考试试题紧扣教学大纲，考点较好地覆盖了大纲规定的知识点，题型结构合理、题量适中、难度中等。图九是表一中笔者任课班级三届本科生的成绩分布图。如图9所示，三届学生的成绩分布比较合理，通过率较高，满足学校要求。每一届学生成绩统计中，高分和不及格学生数量相对较少，成绩分布大致符合正态分布特征，学生对考试成绩总体满意。在每学期的网上教学评价环节，学生对笔者评分均在93分以上，这也体现了学生对该教学方法的认可。

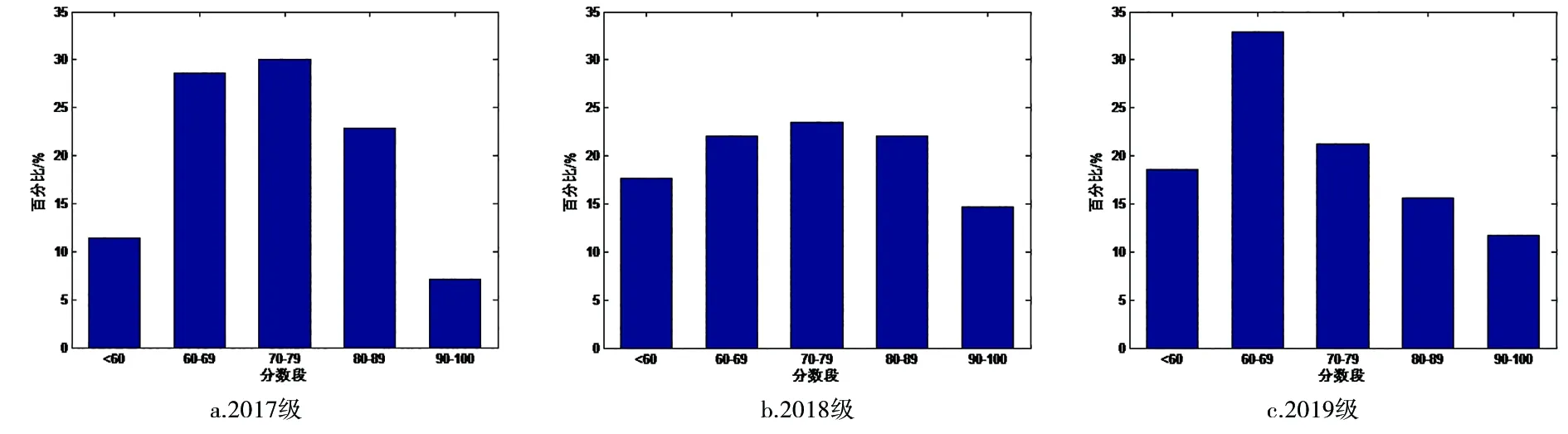
图9 学生成绩分布Fig.9 The distribution of students’ score

在教学过程中，笔者及团队注重与学生的交流并获取反馈。在学习《信号与系统》这门课程的过程中，部分同学们反映，通过对几种傅里叶变换的梳理和总结后，有豁然开朗的感觉，可以在一定程度上强化理解和记忆，并让学生获得攻克难关的成就感，提升学习兴趣。

4 结语

根据高校人才培养目标，结合团队多年教学经验，笔者对信号与系统这门课程中的傅里叶变换进行了教学探索。基于采样定理将傅里叶变换的时、频域分析这部分内容进行了重新组织，使得学生对连续时间傅里叶变换、离散时间傅里叶变换、连续傅立叶级数、离散傅立叶级数、离散傅里叶变换、快速傅里叶变换几个比较类似又容易混淆的概念能够充分理解、深入体会。通过一段时期的教学实践发现，该教学探索能够提高课程教学质量，并取得良好的教学效果。在今后的教学工作中，笔者会不断进行探索和实践，并对教学的方式、方法进行优化，以期进一步提升课程的教学质量。